弯矩作用下热塑性复合材料悬臂梁弹塑性分析*

雷勇军，刘明伟，张大鹏，高艺航

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073； 2. 空天任务智能规划与仿真湖南省重点实验室， 湖南 长沙 410073；3. 中国运载火箭技术研究院 北京宇航系统工程研究所， 北京 100076)

自1951年Bradit首次制造热塑性复合材料(玻璃纤维增强聚苯乙烯)以来，热塑性复合材料已普遍应用于航空工程、汽车交通、医疗器械等领域[1-3]。在当前可重复使用运载器的需求下，具备高抗冲击性能、高损伤容限以及可熔融再加工等特点[4-5]的热塑性复合材料必将在航天工程领域得到更广泛运用。试验表明[6-7]热塑性复合材料具有明显的弹塑性阶段，进入塑性后有较强的承载能力，这与传统的热固性复合材料弹性阶段后即发生脆性断裂有很大不同。为充分发挥材料的应用潜力，避免以弹性设计代替塑性设计的错误[8]，对热塑性复合材料弹塑性力学特性进行分析具有重要意义。

热塑性复合材料具有高度正交各向异性特点，其力学问题可等效为正交各向异性材料的力学问题进行研究。Lekhnitskii[9]得到了受横向力作用的正交各向异性悬臂梁、受均布载荷和线性分布载荷作用的正交各向异性简支梁和悬臂梁的弹性解答。黄德进等[10-11]利用Airy应力函数建立了均布载荷下正交各向异性梁的力学特性分析模型，并得到了两端固支和一端固支一端简支边界条件下应力场和位移场的解析解。针对均布载荷作用下正交各向异性悬臂梁的变形问题，黄立新等[12-13]用有限元法分析了材料各向异性、跨高比等对变形的影响。Klc等[14]分析了在均布载荷或横向集中力作用下复合材料悬臂梁自由端挠度与纤维方向角之间的关系。然而上述文献中应力函数形式很难确定，为解决这一问题，张浪等[15]给出了一种通过求解函数方程获得平面各向异性梁弹性解的新方法。当外载荷较大，材料进入塑性后，相应问题变得更复杂。基于理想弹塑性理论，Aykul和Kaya[16]以及Esendemir[17-18]研究了集中载荷下热塑性复合材料悬臂梁、均布载荷下或集中载荷下简支梁的弹塑性应力问题，然而理想弹塑性理论与实际热塑性复合材料应力应变关系存在较大差异。结合线性强化弹塑性理论和Euler-Bernoulli梁假设，Sayman等[19]对弯矩作用下热塑性复合材料悬臂梁进行研究，得到了弹性解和弹塑性解。对于复合材料短粗梁，Karamanl[20]利用Timoshenko梁理论研究了复合材料层合梁在不同边界条件下的变形问题；Balduzzi等[21]基于Timoshenko梁理论分析了材料的各向异性对梁的本构关系和应力分布的影响；Doeva等[22]给出了考虑拉弯剪扭耦合效应的Timoshenko复合材料梁静挠度分析的精确解析解，并指出现有的Euler-Bernoulli梁模型不足以解释厚梁特性的问题。但是，以上基于Timoshenko梁理论的研究均没有考虑热塑性复合材料的塑性效应。

本文以热塑性复合材料悬臂梁为研究对象，基于Timoshenko梁理论和Tsai-Hill屈服准则，得到应力和位移的解析解。通过与文献[19，21]和有限元计算结果对比，验证本文所给模型与方法的正确性，并分析了纤维方向角、弯矩、跨高比以及纤维体积分数等对悬臂梁应力和位移的影响规律。

1 悬臂梁弹塑性分析模型

研究对象如图1所示，热塑性复合材料悬臂梁长为l、高为2c、厚为t，纤维方向角为θ，自由端承受弯矩M作用，忽略体力，并建立如图所示的坐标系xoy。

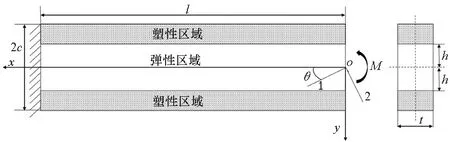
图1 受弯矩载荷的悬臂梁Fig.1 Cantilever beam loading by bending moment

不失一般性，对该悬臂梁进行如下4个基本假设：

1)梁的变形属于小挠度变形；

2)在xoy平面内满足平面应力假设；

3)热塑性复合材料是拉压同性的；

4)悬臂梁变形满足Timoshenko梁理论，轴向位移u、横向位移v和转角φ相互独立，则有

(1)

其中，u0为梁中性面轴向位移，w为梁中性面横向位移。

下面分别建立弹性段和弹塑性段理论分析模型。

1.1 弹性段分析模型

考虑悬臂梁的平面应力问题，基本方程如下：

1)平衡方程

(2)

2)几何方程

(3)

3)本构方程

(4)

在纤维坐标系1o2下，热塑性复合材料的本构关系为

(5)

(6)

其中，转换矩阵T的表达式为

(7)

设应力函数为φ(x,y)，其与应力σx、σy和τxy的关系为

(8)

结合式(3)、式(4)和式(8)得控制方程

(9)

梁仅在自由端承受弯矩M，因此在梁任意截面上可以得到

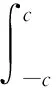
(10)

由弯矩M为给定常值可知，σx只与坐标y有关，结合式(8)可得应力函数的表达式为

φ=F(y)+yA(x)+B(x)

(11)

其中，F(y)、A(x)、B(x)为待求函数，对于本悬臂梁，其上下表面为主要边界条件，则有

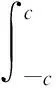
推导可得在弯矩M作用下悬臂梁弹性阶段应力场和位移场为

(12)

由式(12)可知，当弯矩M较小时，梁处于弹性阶段，梁上下表面处应力最大；随着M增大，梁上下表面先进入塑性状态，需结合复合材料塑性力学知识建立弹塑性段分析模型。

1.2 弹塑性段分析模型

文献[23-25]表明Tsai-Hill屈服准则描述的应力空间屈服面与热塑性复合材料真实屈服状态吻合，本文基于Tsai-Hill屈服准则对热塑性复合材料悬臂梁弹塑性段应力和变形进行分析，平面应力假设下考虑拉压同性的Tsai-Hill屈服准则如下：

(13)

其中，X为复合材料沿纤维方向屈服强度，Y为垂直纤维方向屈服强度，S为面内剪切强度。根据式(13)，定义等效应力为

(14)

根据坐标转换矩阵，材料主轴坐标系下应力σ1、σ2、τ12和xoy坐标系下应力σx、σy、τxy的转换关系为：

(15)

由于σy=0、τxy=0，将式(15)代入式(14)中，可得等效应力表达式为

(16)

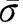
(17)

其中，σ0的大小为X，K是塑性常数，则复合材料屈服时满足如下关系：

(18)

其中，X1为复合材料达到屈服条件时应力σx的大小，即当σx=X1时，材料进入塑性。选用相关塑性流动法则，在纤维坐标系1o2下塑性应变增量表达式为

(19)

总应变增量为弹性应变增量和塑性应变增量之和，即dε=dεe+dεp，则纤维坐标系1o2下总应变增量为

(20)

对式(20)进行积分，可得到纤维坐标系1o2下各应变分量，再利用坐标转换关系，将其变换到xoy坐标系下，可得xoy坐标系下总应变为

(21)

其中，B1、B2和B3为与材料塑性性能和纤维方向角有关的参数。梁在出现屈服后，结合Timoshenko梁理论可得

(22)

由1.1节分析可知，σx与坐标y成正比例关系，梁的塑性区域从梁上下表面向中性面扩展，设y∈(-h,h)为弹性区域，则在弹塑性分界位置存在σx=X1，可得

(23)

由式(23)并结合转角边界条件φ(l,y)=0得

(24)

(25)

因此考虑塑性后，悬臂梁的应力解如下：

(26)

在梁的任意截面均满足如下关系：

(27)

基于Timoshenko梁理论并结合式(24)，可得轴向位移为

(28)

由式(3)和式(21)积分可得横向位移在弹性区域和塑性区域分别为

(29)

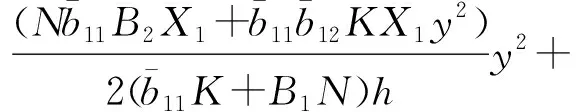
(30)

其中，Ve(x)和Vp(x)为与x相关的待求函数。进一步由边界条件ve(l,0)=0、vp(l,h)=0和连续性条件ve(x,h)=vp(x,h)可得横向位移的表达式为

(31)

(32)

以上分析将Timoshenko梁理论和塑性线性强化理论应用于热塑性复合材料悬臂梁的弹塑性分析中，并获得了梁应力和变形的解析解。此外，由于热塑性复合材料的力学性能与纤维体积分数vf有关[26-27]，本文所建模型可用于分析不同纤维体积分数下热塑性复合材料悬臂梁弹塑性力学特性。

2 算例分析

2.1 模型验证

文献[19]基于Euler-Bernoulli梁理论和线性强化弹塑性本构模型分析了弯曲载荷下热塑性复合材料悬臂梁弹塑性应力和变形；文献[21]基于Timoshenko梁理论分析了在弯曲载荷下双层复合材料悬臂梁的弹性静变形。为验证本文所建模型及求解方法的正确性，以文献[19]中的编织钢纤维增强聚乙烯复合材料悬臂梁为例进行对比分析，算例中涉及的基本参数与文献[19]一致：悬臂梁长80 mm、高12 mm、厚6.4 mm，弹塑性力学参数如表1所示。设θ为45°，M为4 kN·mm。此外，本节给出了梁有限元计算结果，有限元计算采用四节点双线性平面应力四边形单元，共计2 600个单元，屈服准则为各向异性Tsai-Hill屈服准则[28]，硬化方式为各向同性硬化。

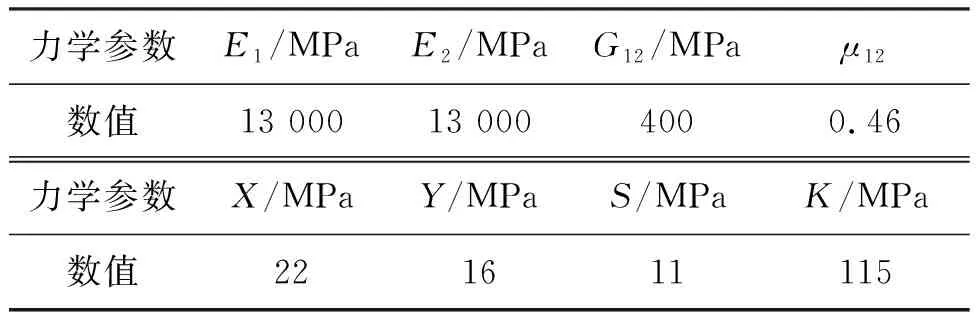
表1 编织钢纤维增强聚乙烯复合材料力学参数

图2给出了本文模型与参考文献[19，21]以及有限元计算在悬臂梁固定端截面应力分布对比结果。由图2(a)可知，在不考虑塑性的情况下，以上方法获得的数据吻合较好；由图2(b)可知，在考虑塑性的情况下，本文所建模型与有限元计算结果更接近。对比图2(a)和图2(b)可知，塑性效应会显著改变悬臂梁截面应力分布形式。表2给出了以上方法在自由端下表面点(0 mm,6 mm)的应力和位移。由表2可以看出，本文模型所得数据较文献[19]均更接近于有限元计算结果，特别是在考虑塑性的情况下，轴向位移和横向位移较文献[19]的Euler-Bernoulli梁模型提高了1.81%和2.03%的计算精度。以上分析验证了本文所建模型和求解方法的正确性，说明了在热塑性复合材料悬臂梁弹塑性力学分析中，运用Timoshenko梁理论可显著提高求解精度。下面基于本文模型对纤维方向角、弯矩、跨高比以及纤维体积分数等对梁应力和变形的影响做进一步分析。

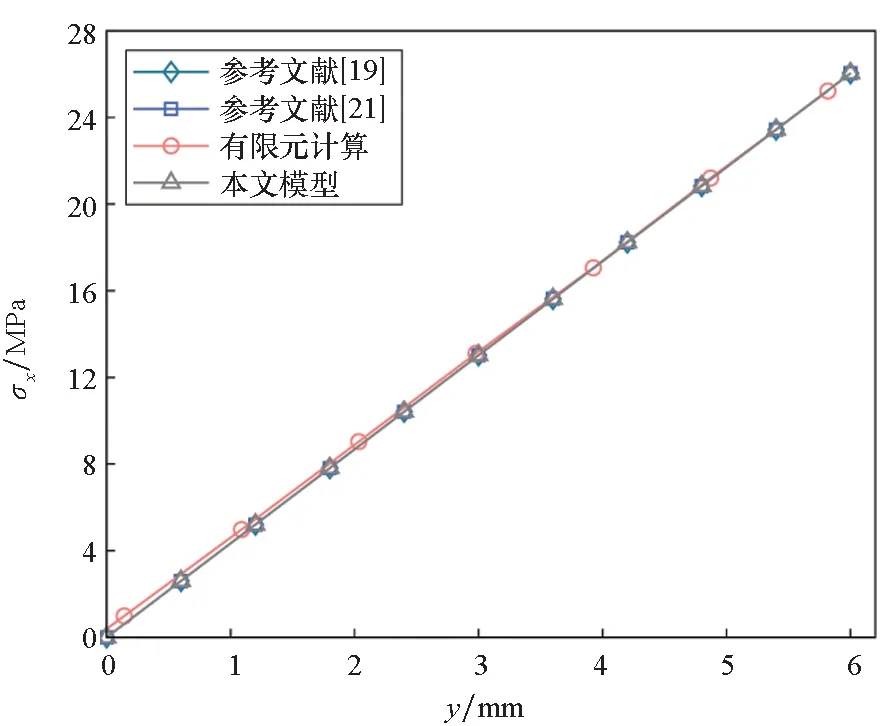
(a) 不考虑塑性(a) Not considering plasticity

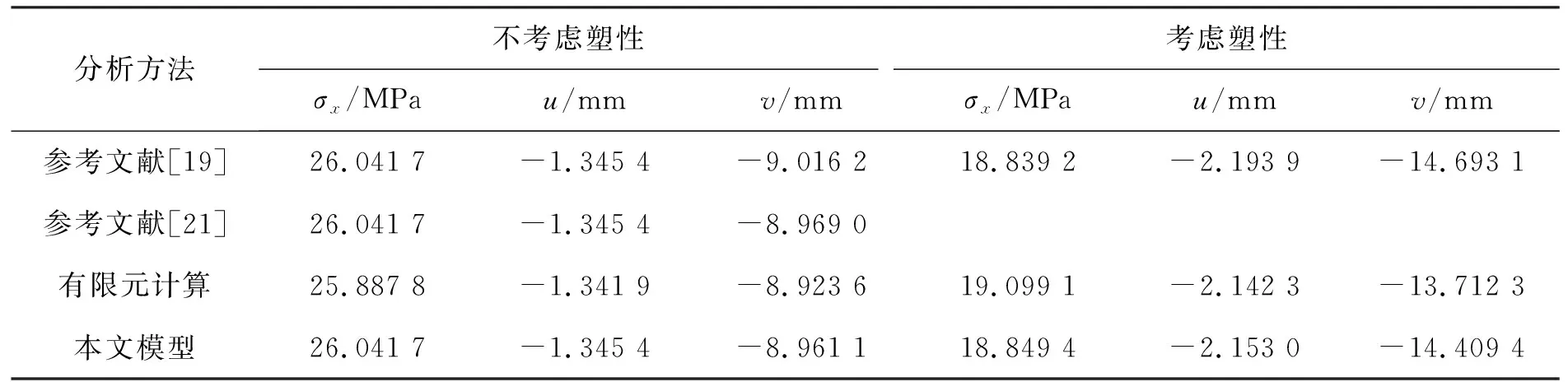
表 2 参考点(0 mm，6 mm)应力、位移

2.2 影响因素分析

2.2.1 纤维方向角对悬臂梁弹塑应力和位移的影响

图3分别给出了纤维方向角θ对弹塑性区域参数h、梁自由端下表面点应力σx、轴向位移u以及横向位移v的影响情况。在本算例中，梁的几何参数和弹塑性力学参数同2.1节。

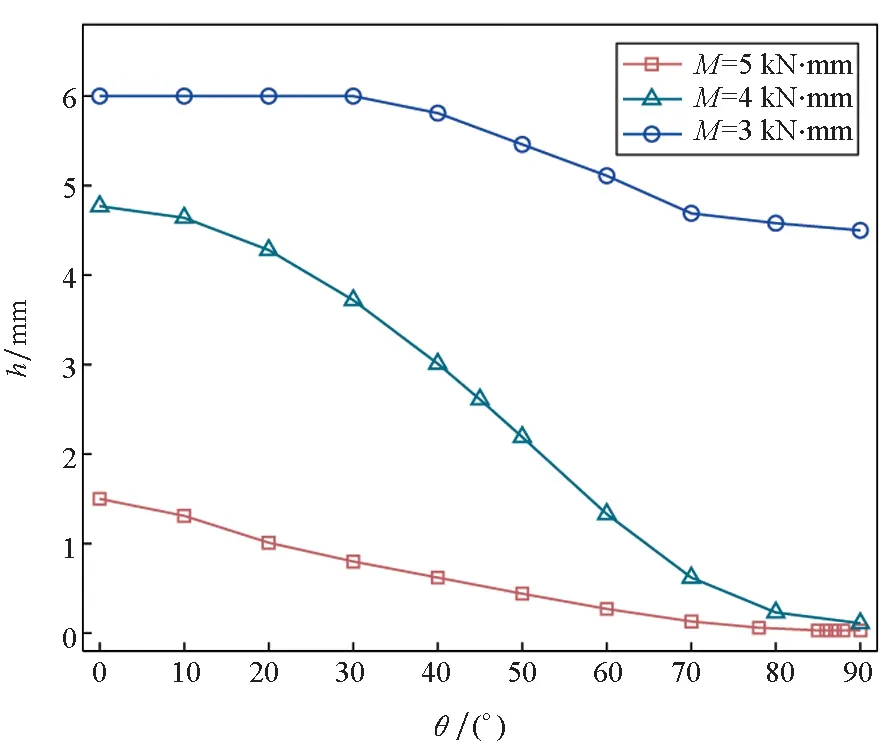
(a) 参数h随纤维方向角θ的变化曲线(a) Relation of parameter h and fiber orientation angle θ

由图3(a)可知，在不同M作用下，h均随着θ增大而减小，h越小表明梁处于塑性的区域范围越大，这说明增大θ会显著降低梁的刚度，且该影响随着M的增大而增强。

由图3(b)可知，当M为3 kN·mm且θ不超过30°时，σx几乎不受θ的影响。在此条件下参考点处于弹性状态，由式(12)可知该状态下应力大小与纤维方向角无关。当参考点处于塑性状态时，参考点应力与纤维方向角的关系分两种情况：当M较小时，σx随θ增大而减小；当M较大时，σx随θ的增大而先增大后减小。塑性应力σx的解析表达式(26)可对上述变化做出解释。由式(26)可知，塑性应力σx与塑性各向异性参数N成反比而与等效塑性应变εp成正比，又由N的表达式可知N随θ的增大而增大，式(25)表明εp与h成反比，h随θ的增大而减小。

由图3(c)和图3(d)可知，当M为3 kN·mm且θ小于30°时，参考点的位移随θ增大而增大，注意在此情况下，参考点处于弹性状态。当参考点进入塑性状态后，不同弯矩作用下的位移随纤维方向角的变化表现出不同的规律，位移解析式可对此做出合理解释。以轴向位移u为例，由式(28)可知，轴向位移u与弹塑性区域参数h成反比、与X1成正比，结合式(18)，X1与参数N成反比，由此可知轴向位移u与h和N的乘积成反比。下面结合图3(c)中M为5 kN·mm的情况做进一步解释，由图可知u随θ增大而先增大后减小，这是由于参数N与参数h的乘积随θ增大而先减小后增大。横向位移v的分析也如此，在此不做过多赘述。

2.2.2 弯矩对悬臂梁弹塑应力和位移的影响

为进一步分析弯矩M和纤维方向角θ对梁应力和位移的影响，在本算例中，θ分别为0°、30°和60°，梁的其他几何参数和材料参数同2.1节。图4分别给出了在给定纤维方向角下，梁弹塑性区域参数h、梁自由端下表面点应力σx、轴向位移u和横向位移v与弯矩M之间的关系。

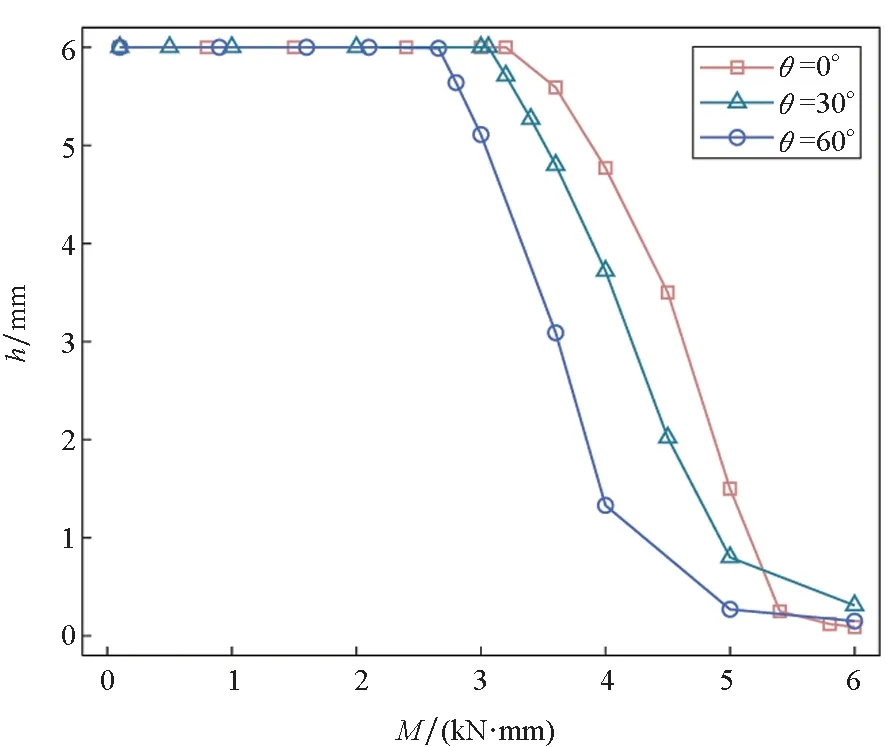
(a) 参数h随弯矩M的变化曲线(a) Relation of parameter h and moment M

由图4(a)可知，h随着M的增大先保持不变后快速减小。当M较小时，梁并未出现屈服，h大小始终为梁高的一半，随着M增大，梁上各点逐渐屈服，导致h显著减小。

由图4(b)可知，在梁截面出现屈服前，σx随着M增大而线性增大，在屈服后，σx随着M先缓慢增大后快速增大。由式(26)可知，σx与h成反比，当梁刚屈服时，h值较大因而σx增加缓慢，随着M继续增大，梁截面塑性区域面积增加，h显著减小，从而导致σx迅速增大。

由图4(c)和图4(d)可知，当M较小时，参考点处于弹性状态，此时位移随M增大而缓慢增大，当参考点屈服以后，其位移随着M增大而迅速增大。此外，从图中可以看出当θ为60°且M超过4 kN·mm时，参考点的位移尤其是横向位移v已经很大，此时已不满足小变形假设。

2.2.3 跨高比对悬臂梁弹塑应力和位移的影响

在分析跨高比l/(2c)对梁应力和位移的影响时，用h/c表征弹性区域占整个截面面积的比例，h/c的值越接近1，说明梁截面弹性区域面积越大。图5分别给出了在不同载荷下h/c以及梁自由端下表面参考点的应力σx、轴向位移u、横向位移v与跨高比l/(2c)的关系。在本算例中，通过改变梁高度2c来改变梁跨高比，纤维方向角θ固定为30°，梁其他几何参数和材料参数同2.1节。

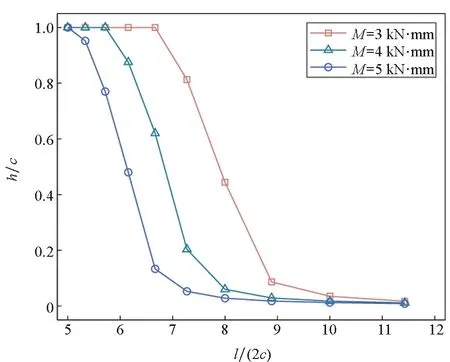
(a) 参数h/c随跨高比l/(2c)的变化曲线(a) Relation of parameter h/c and aspect ratio l/(2c)

由图5(a)可知，随着跨高比l/(2c)增大，h/c的值从1逐渐减小至0，且跨高比l/(2c)大于9时，梁截面已完全进入塑性状态。这说明在梁长度一定的情况下，梁的高度越小，梁更易屈服。由图5(b)可知，跨高比l/(2c)越大，σx值越大，而且M越大，σx随跨高比l/(2c)增加得越快。参考点的变形情况与跨高比l/(2c)的关系如图5(c)和图5(d)所示，无论是轴向位移还是横向位移，当跨高比l/(2c)较小时，其随跨高比l/(2c)的增加而增加缓慢，当跨高比l/(2c)较大时，其随跨高比l/(2c)的增加而增加迅速。由以上分析可知大跨高比梁结构偏柔，更易屈服。由图可以看到，当跨高比l/(2c)大于8时，参考点的变形量已超出小变形假定的范围。

2.2.4 纤维体积分数对悬臂梁弹塑性区域分布和应力的影响

本小节分析纤维体积分数vf对悬臂梁应力和弹塑性区域分布的影响。在本算例中悬臂梁材料为芳纶纤维增强聚丙烯复合材料，其力学参数同文献[26]一致，详细如表3所示，梁其他几何参数和材料参数同2.1节，设置两种工况：①外载荷M=3 kN·mm、纤维方向角θ=30°；②外载荷M=2 kN·mm、纤维方向角θ=45°。图6给出了当vf在10%至25%之间时，梁自由端下表面点应力σx和弹塑性区域参数h随其的变化曲线。

表3 芳纶纤维增强聚丙烯复合材料力学参数

由图6(a)可知，vf越大，σx越小。由表3可知，随着vf增加，复合材料弹性力学性能均提高，相同弯矩作用下，σx越小。由图6(b)可知，随着vf增加，两种工况下参数h均逐渐减小。当vf=10%时，h接近于6 mm，整个梁截面处于弹性状态；当vf=25%时，h接近于0，整个梁截面处于塑性状态。由表3可知，在塑性力学参数方面，随着vf增加，纤维方向屈服强度增大，但垂直纤维方向以及面内剪切屈服强度显著降低。根据Tsai-Hill屈服准则，复合材料整体更易屈服，因此在相同弯矩作用下，纤维体积分数越大，梁截面塑性区域面积越大。

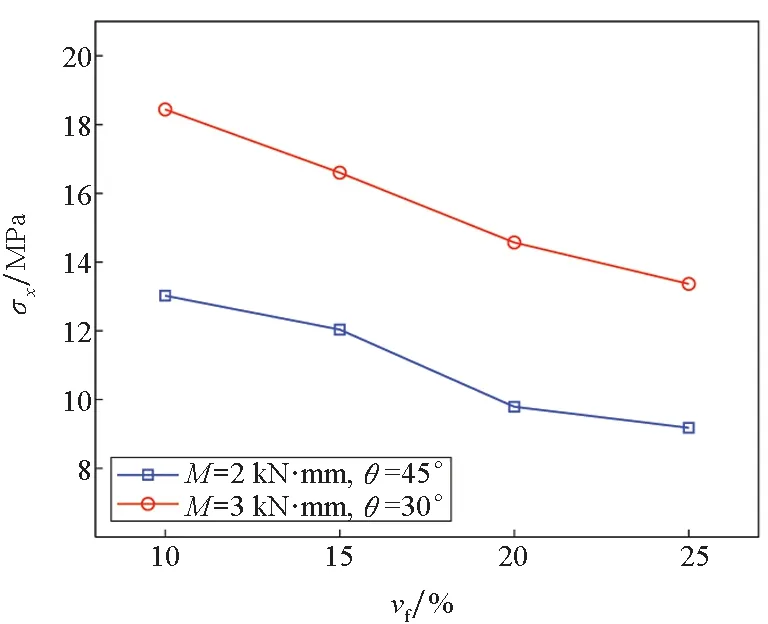
(a) 应力σx随纤维体积分数vf的变化曲线(a) Relation of stress σxand fiber volume fraction vf

3 结论

本文基于Timoshenko梁理论和Tsai-Hill屈服准则建立了弯矩作用下热塑性复合材料悬臂梁弹塑性分析模型，得到了应力和位移的解析解，并对梁截面弹塑性应力和变形的影响因素进行了分析，主要结论包括：

1)在热塑性复合材料悬臂梁弹塑性特性分析中，基于Timoshenko梁理论得到的应力和位移精度更高。对于编织钢纤维增强热塑性复合材料，本文模型所得轴向位移和横向位移分别比Euler-Bernoulli梁理论提高了1.81%和2.03%。

2)纤维方向角θ和弯矩M综合影响热塑性复合材料悬臂梁力学特性，当M较大时，截面最大应力和位移随着θ增大而增大；当M较小时，截面最大应力随着θ增大而减小，位移随着θ增大而先增大后减小。

3)跨高比l/(2c)显著影响热塑性复合材料悬臂梁弹塑性力学特性，在相同弯矩作用下，跨高比l/(2c)越大，截面最大应力和位移越大，梁截面塑性区域面积相对越大，且当跨高比l/(2c)超过9时，热塑性复合材料悬臂梁已完全进入塑性状态。

4)当单向纤维增强聚丙烯复合材料纤维体积分数由10%增加至25%时，悬臂梁由弹性状态进入完全塑性状态，且随着纤维体积分数增加，悬臂梁截面最大应力逐渐减小。

以上结论可为热塑性复合材料悬臂梁设计应用提供参考，在后续研究中，将进一步考虑热塑性复合材料拉压异性的力学特性建立相关结构的力学模型。