含气膜孔涡轮叶片寿命可靠性设计优化中的网格参数化方法*

雷婧宇，吕震宙，贾贝熙

(西北工业大学 航空学院， 陕西 西安 710072)

涡轮叶片长期承受着多种载荷的复合作用[1-3]。叶片气膜孔的位置和形状往往会影响其局部应力，进而对寿命造成影响。气膜孔的几何尺寸、叶片承受的载荷以及叶片材料属性等都具有不确定性，因此，十分有必要研究含气膜孔涡轮叶片寿命的可靠性设计优化[4-7]。

在可靠性设计优化的数值仿真中，由于气膜孔几何参数的改变，有限元分析的实现需要网格自动随几何构型参数化改变。叶片结构分析中，其加强肋、绕流柱等都对结构响应有影响，因而对真实几何结构不能作过多化简。由于气膜孔的几何参数存在变异性，其数值仿真需要大量的样本模拟，与之相应的有限元分析过程也需要多次调用。因此，针对含气膜孔涡轮叶片寿命可靠性设计优化的网格提出了以下几点要求：

1)对真实几何构型的简化处理不能过多；

2)网格随几何构型参数化改变；

3)在保证计算精度的前提下，网格数量尽量少，以减少有限元分析的耗时。

已有的文献中，周正贵[8]对叶片翼型进行了二维参数化网格设计；李立州等[9]利用网格变形技术，采用含翼型截面的实心叶片模型，实现了多学科设计优化中结构变形向气动网格的变形传递；史振[10]对叶片整体结构分解，实现了参数化几何设计，其中叶片结构包含冷却通道、绕流柱、气膜孔等基本特征，网格采用了非结构化的四面体网格划分，网格数量达3 600万左右；杨帆[11]利用自由网格变形技术和边界网格变形方法，实现了不同学科分析网格的协调变形，该叶片构型比较简单，不包含气膜孔结构，采用结构化网格，对叶片壁厚进行了可靠性多学科设计优化；李磊等[12]利用自由变形技术发展了协调流场与结构分析网格的参数化变形方法，实现了对叶片翼型的多学科设计优化，该叶片不包含冷却通道、气膜孔等结构；岳孟赫等[13]实现了涡轮冷却叶片的参数化控制分析，其叶片结构包含了气膜孔、绕流柱、加强肋、尾缘劈缝等，与真实叶片构型十分接近，采用结构化网格，网格总数为459万。

由此可见，目前针对涡轮叶片可靠性设计优化的网格参数化方法分为两类：一类为以叶片翼型为代表的外形优化，采用结构化网格实现网格参数化，对叶片真实构型的简化较多，且不包含气膜孔结构，无法用于气膜孔的设计优化中；另外一类以叶片真实构型为基础，对叶片进行几何、网格参数化，但最终生成的网格数量庞大，单次有限元分析耗时长，在需要多次调用有限元分析的可靠性设计优化中，耗费时间无法接受。

结构化的网格虽然协调变形方便，但其在前期画网格十分费时，且对操作人员的技术要求和经验要求非常高。相比结构化网格，非结构化的网格在适应复杂外形、实现网格分块等方面更具优势[14-15]。因此，针对含气膜孔涡轮叶片的局部几何优化，本文提出了非结构局部网格参数化方法，实现了其可靠性优化设计。由于局部参数化的方法对非参数化区域的网格没有限制，其网格灵活性更强，这样一方面能适应复杂的边界外形，另一方面方便调整非参数化区域的网格数量。相比结构化网格，该方法的网格更加灵活，能够在保证计算精度的同时极大地减少网格总数量，减小有限元的计算时间成本。

1 涡轮叶片的网格参数化变形

涡轮叶片几何构型复杂，有限元分析的整个过程需要分别在几何建模软件、网格划分软件以及有限元后处理软件(如CATIA、HYPERMESH、ANSYS)中完成。由于气膜孔位置和形状参数改变后，叶片中远离气膜孔的大部分几何构型并未改变，可利用CATIA构建不含气膜孔的叶片几何模型，在HYPERMESH软件中完成气膜孔及网格划分。气膜孔位置和形状参数更新后，使用不含气膜孔的几何构型、非参数化区域的网格模型作为初始模型，重构气膜孔以及参数化区域的网格。该方法不再需要使用CATIA进行几何重构，因而减少了多个软件联合带来的信息误差或者失真。

1.1 涡轮叶片的几何模型

依据某型号高压涡轮一级转子叶片，对其进行适当简化处理，得到如图1所示的叶片几何模型。叶片由叶身、挡板和榫头组成，含冷气通道，由榫头底部通入冷气。叶身由8个叶型剖面扭转变形获得，内部空心含加强肋，尾部分布有绕流柱，尾缘劈缝。以发动机轴向为x轴，顺气流方向为正；发动机径向为z轴，离心方向为正；y轴由右手螺旋法则确定。气膜孔分布于两个加强肋之间，呈一列形式。

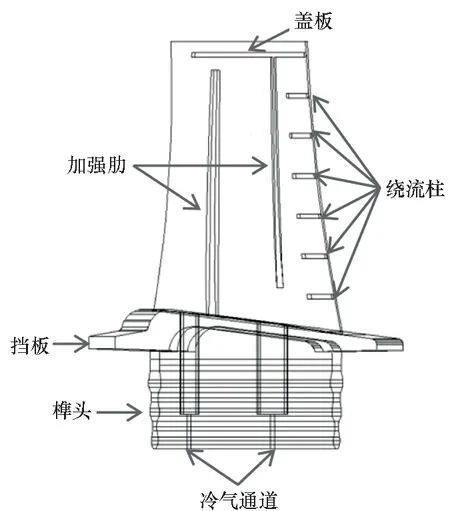
图1 叶片几何模型Fig.1 Geometric graph of turbine blade

1.2 网格模型

1.2.1 参数化网格与非参数化网格的区域划分

鉴于非结构化网格的灵活性更强，为了减少网格的数量、缩短整个网格划分工作的时间成本，采用非结构化网格对含气膜孔涡轮叶片进行网格划分。但是，如果在每一次更新几何模型后重构所有网格，必然会导致网格模型的生成周期变长。对于涡轮叶片气膜孔的局部优化问题，由于气膜孔位置和形状改变只会对附近的网格造成影响，远端的网格基本不受影响，保持距离气膜孔较远的几何模型以及网格模型不变，在每次迭代中更新气膜孔的几何构型以及气膜孔周围的网格，则可以极大地减少几何更新以及网格重构的工作量，提高生成网格模型的效率。考虑气膜孔变化后对网格形状影响大的区域，将叶片的网格模型分为参数化区域和非参数化区域，以xz平面为基准面，设计矩形交界线，沿y轴方向切割形成交界面，如图2所示。

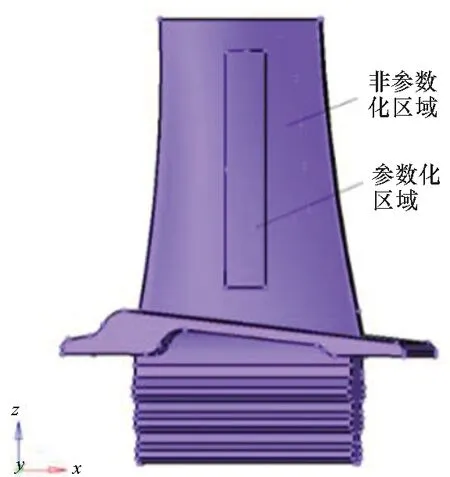
图2 叶片区域划分示意Fig.2 Region separation of turbine blade

1.2.2 非参数化区域的网格

参数化区域与非参数化区域在同一个结构中，在交界面必须保持节点一致，因此，在交界面上二者共用控制点。要确定非参数化区域的网格，必须首先确定其与参数化区域交界面上的控制点。

确定交界面上控制点的步骤如下：

1)根据气膜孔的初始半径和位置，以气膜孔圆心在xz基准面的投影为正方形的中心点，x轴、z轴方向分别为正方形四条边的两个矢量方向，在xz基准面设计包络气膜孔应力集中区域的正方形；

2)在xz基准面延长步骤1中正方形的各边边长；

3)将正方形各边边长的延长线与矩形交界线的交点作为非参数化区域保持不动的控制点，如图3所示。

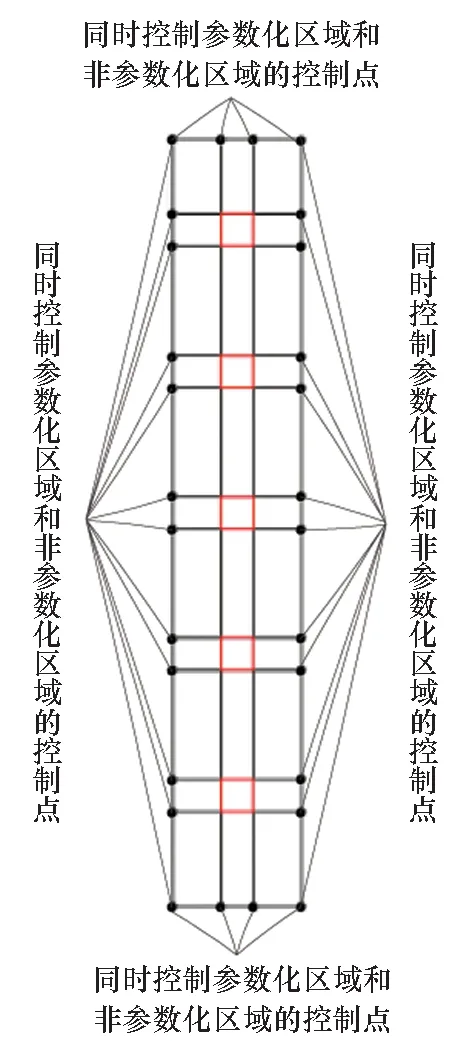
图3 交界面处的控制点示意Fig.3 Control points on the interface

对叶片的非参数化区域进行划分，以参数化和非参数化区域的交界面为起点划分网格，依次向周围扩展，最终在叶片非参数化区域生成以六面体为主的网格模型。非参数化区域的块划分如图4所示，网格模型如图5所示。将网格模型导入ANSYS有限元分析软件中，对其网格质量进行评估，结果如表1所示。

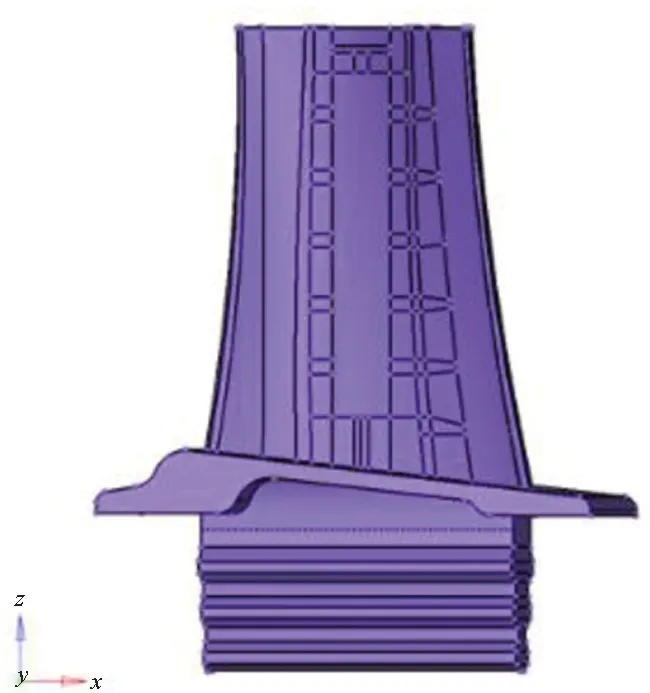
图4 非参数化区域划分Fig.4 Blocks in non-parameterized region

图5 非参数化区域网格Fig.5 Meshes of non-parameterized region

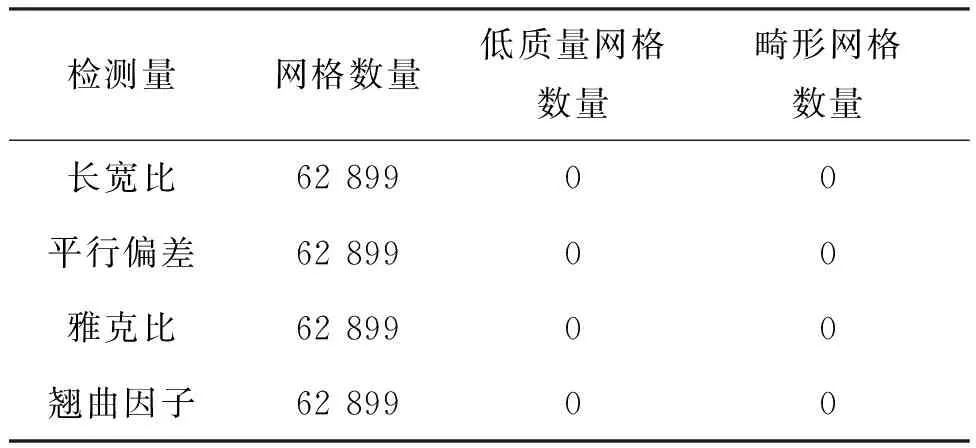
表1 非参数化区域网格质量检测

1.2.3 参数化区域的网格

参数化区域包络了气膜孔以及气膜孔变化后网格变形较大的区域。在有限元分析中需要对孔周围的结构响应重点关注，因此孔周围网格相对于结构其他部分更密。确定参数化区域控制点的步骤如下：

1)根据气膜孔的初始半径和位置，以气膜孔圆心在xz基准面的投影为正方形的中心点，x轴、z轴方向分别为正方形四条边的两个矢量方向，在xz基准面设计包络气膜孔应力集中区域的正方形；

2)在xz基准面画正方形的对角线，作为辅助线设计气膜孔应力集中区域的网格；

3)在xz基准面延长正方形的各边边长作为辅助线；

4)将正方形对角线与圆的交点以及正方形的四个顶点作为随设计参数移动的控制点；

5)正方形各边边长的延长线与矩形交界线的交点作为保持不动的控制点，这些控制点即是参数化区域与非参数化区域交界面的控制点。

随设计参数移动的控制点坐标通过几何关系来确定。设气膜孔的半径为r，孔间距为D，孔相对于初始位置的左右移动距离和上下移动距离分别为L和M，xz基准面上定位孔的圆心坐标为Cm(xm,0,zm)，确定随设计参数关联移动控制点的过程如下：

1)根据定位孔的圆心坐标以及孔间距D，计算得到其他各个定位孔的圆心坐标Ci(xi,0,zi)(i=1,2,…，n)，其中i为孔编号，n为一列气膜孔的个数。

2)第i个孔随设计参数关联移动的控制点中，正方形对角线与圆的交点di1、di2、di3、di4的坐标分别为：

3)第i个孔随设计参数关联移动的控制点中，正方形四个顶点ddi1、ddi2、ddi3、ddi4的坐标分别为：

ddi1(xi+L+4×r,0,zi+M+4×r)

ddi2(xi+L+4×r,0,zi+M-4×r)

ddi3(xi+L-4×r,0,zi+M-4×r)

ddi4(xi+L-4×r,0,zi+M+4×r)

随设计参数关联移动的控制点示意如图6所示。

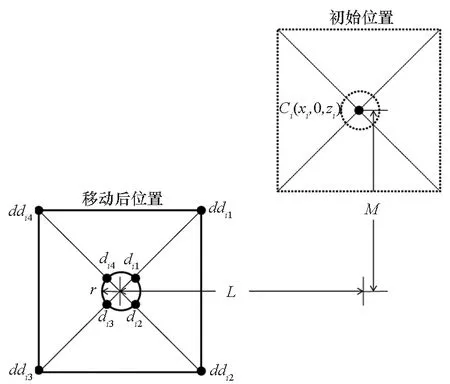
图6 随设计参数关联移动的控制点的示意Fig.6 Schematic diagram of control points moving with design parameters

1.3 网格验证

在每次更新气膜孔的半径及位置后，依据参数化的控制点生成辅助线，对叶片的参数化区域进行面分割，生成二维网格，以二维网格映射获得三维的六面体网格。以孔间距D=10.5 mm、孔的初始半径r0=0.3 mm，孔半径增加0.1 mm,相对于初始位置上移0.1 mm、左移0.3 mm为例，其网格的变形如图7所示。雅克比能够表示网格偏离理想形状的程度，是衡量网格质量最重要的参数。取参数化变形前后的网格，其雅克比如表2所示，可以看出变形前后网格质量良好。

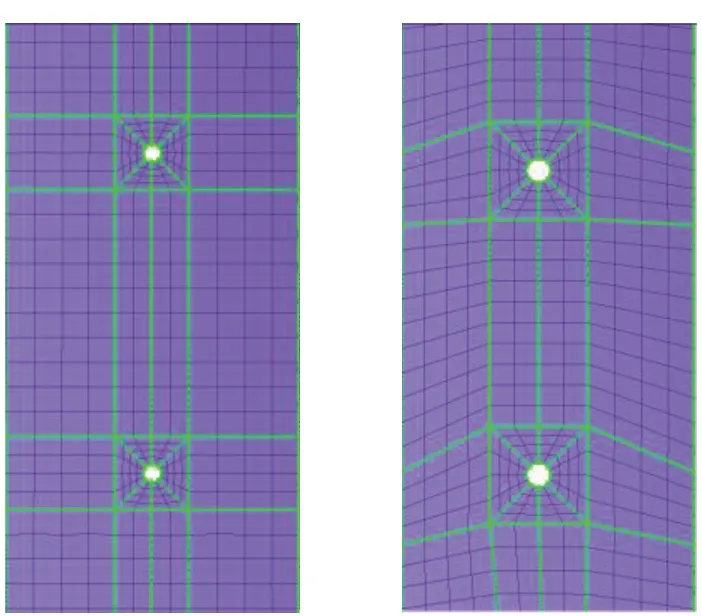
(a) 变形前(a) Before deformation (b) 变形后(b) After deformation

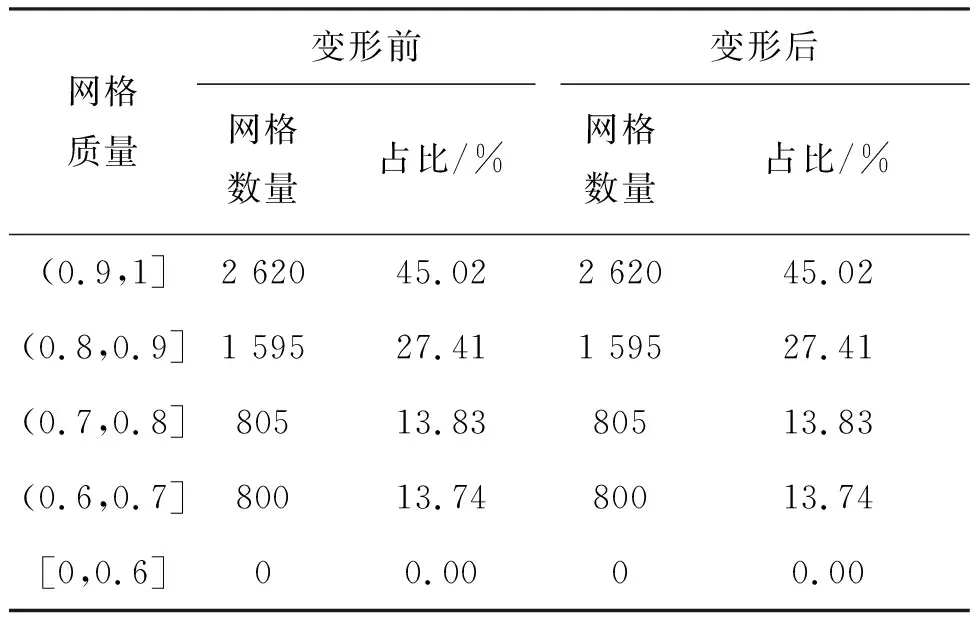
表2 变形前后雅克比检测

在每次优化迭代中，以不含气膜孔的几何构型、非参数化区域的网格模型作为初始模型，在HYPERMESH软件中根据气膜孔的半径和位置参数完成气膜孔的几何结构以及参数化区域的网格，最终生成的网格模型如图8所示。其中，叶身部分以六面体单元为主，榫头采用六面体单元；挡板由于形状不规则，且作为叶身和榫头网格的过渡，采用节点和形状适应性更好的四面体单元。共计68 719个单元。

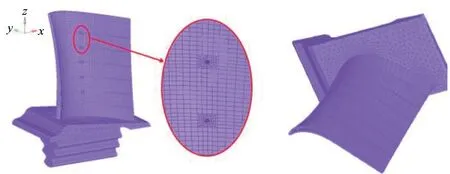
图8 叶片网格模型Fig.8 Meshes of turbine blade

在ANSYS有限元软件中，选取涡轮叶片的三个典型工作状态——最大状态、慢车状态、巡航状态，根据对应的工作载荷对涡轮叶片在三种工作状态下进行加载。为了简化有限元分析过程，将流场视为稳态场并简化为等效力和力矩，对叶片施加温度载荷、气动力载荷、离心载荷，进行热力耦合分析，获得叶片校核点处的结构响应。图9为叶片在最大工作状态下分别利用结构化网格(共计964 141个单元)与局部参数化方法所生成的非结构化网格(共计68 719个单元)获得的有限元应力云图，表3～5为三个典型工作状态下的计算结果。可以看出，在最大工作状态下，叶片的最高应力值出现在最底部孔的应力集中区域，局部参数化方法所生成网格的计算结果与结构化网格的计算结果基本一致，而计算时间相比结构化网格大大减少。结构化网格模型在有限元中对计算机内存要求很高，且单次有限元计算耗时长，在需要多次调用有限元计算的可靠性设计优化中难以被接受。此外，结构化网格前期拓扑块划分十分费时费力，整个网格划分工作时间成本高。

(a) 结构化网格的叶身应力云图(a) Contour plot of the blade by structured mesh

表3 最大状态下结构化网格与局部参数化法网格的计算结果

表4 慢车状态下结构化网格与局部参数化法网格的计算结果

表5 巡航状态下结构化网格与局部参数化法网格的计算结果

文献[16]中提到，可以通过与两倍数量的网格计算结果进行比较来检验网格尺寸是否合理，若结果没有显著差别，则当前网格划分尺寸是合适的。为了进一步检验网格的有限元计算精度，对不同数量的网格模型进行有限元分析，其结果如表6～8所示。由表6～8可见，数量为68 719的网格模型计算精度与数量为125 387和207 270的网格模型结果基本一致，而计算时间则显著减少；数量为39 974、52 549的网格虽然计算时间少，但其最大状态下应变的计算误差较大。因此，综合考虑计算误差和计算时间，选择数量为68 719的网格作为可靠性优化网格模型。非结构局部网格参数化方法在保证有限元计算精度的同时，极大缩减了有限元模型的网格数量，该方法可以有效提高可靠性设计优化的效率。

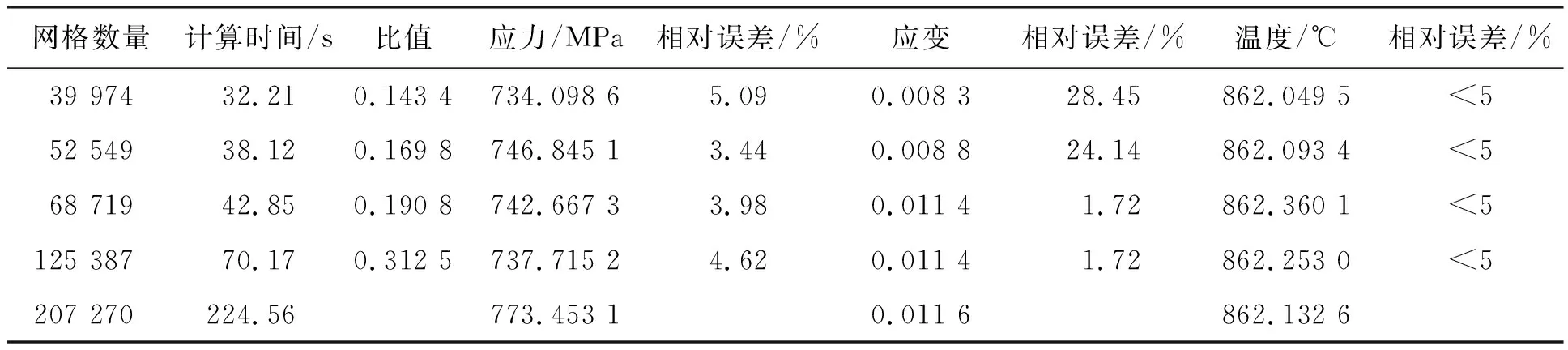
表6 最大状态下不同数量网格的计算结果

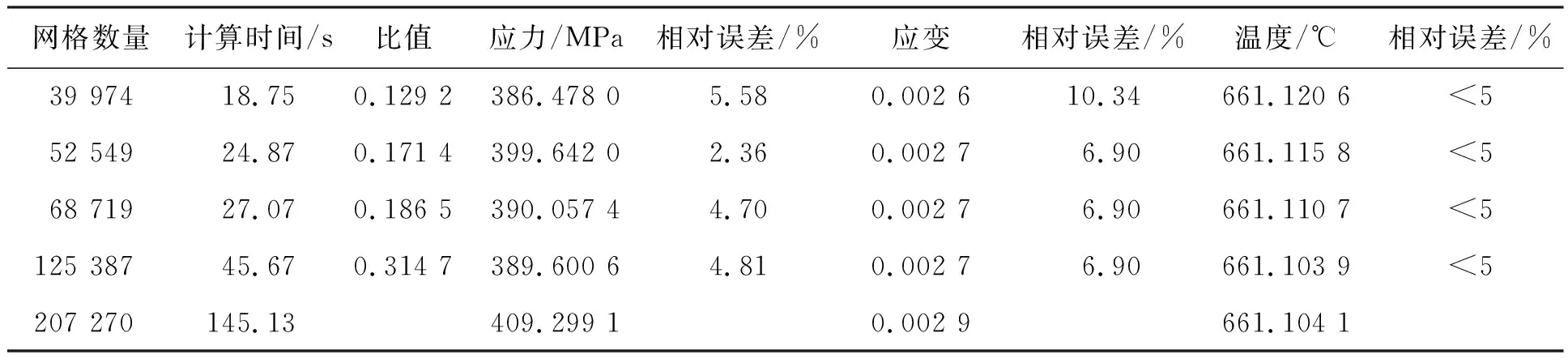
表7 慢车状态下不同数量网格的计算结果

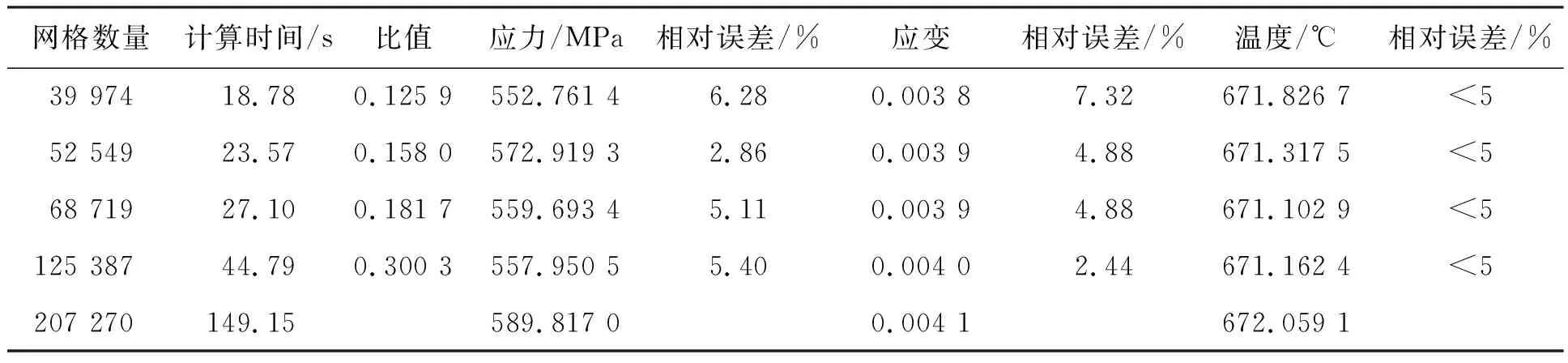
表8 巡航状态下不同数量网格的计算结果

2 可靠性设计优化

选取航空发动机的三个典型工况(零—最大—零、慢车—最大—慢车、巡航—最大—巡航)，根据三个工况中的载荷条件对含气膜孔涡轮叶片进行蠕变-疲劳以及高周-低周复合寿命预测。考虑到寿命的不确定性，以寿命均值μ(N)最大为优化目标，寿命大于1 000次循环的概率大于98%作为可靠度约束，建立优化模型，设计气膜孔半径的均值μ(r)、相对于初始位置的上下移动距离M、相对于初始位置的左右移动距离L。优化模型如下所示：

其中，NLC为涡轮叶片的蠕变-疲劳复合寿命，NLH为高周-低周复合寿命，Pr(·)表示概率算子。

从涡轮叶片的材料性能和工作载荷来考虑不确定性变量对寿命的影响，其中工作载荷与发动机的工作状态相关，而叶片的材料性能与温度相关。选取对叶片寿命影响较大的载荷与材料参数作为随机变量，假设各变量服从正态分布，变异系数为1%，其均值参数如表9和表10所示。

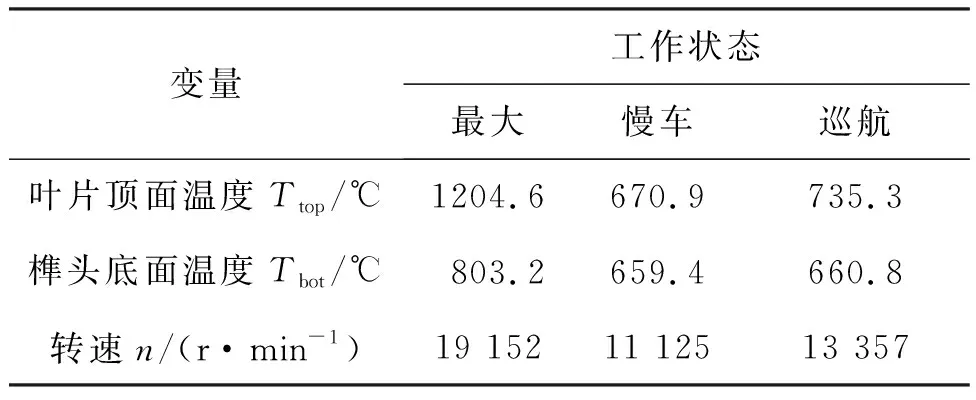
表9 与工作状态相关的不确定性变量的均值参数

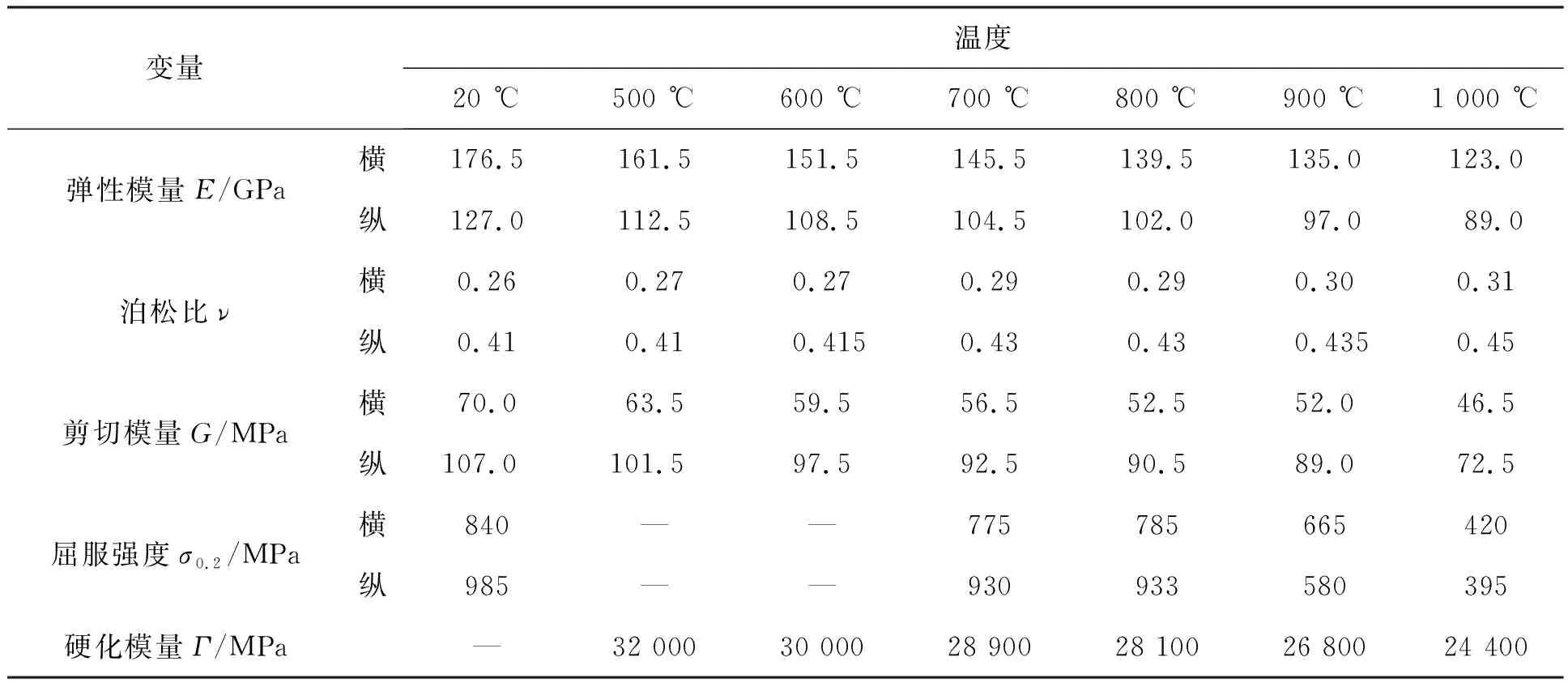
表10 与温度相关的不确定性变量的均值参数

分别建立目标函数与设计变量之间的关系以及约束函数与设计变量之间的关系[17-18]，解除优化求解和可靠性分析求解的嵌套耦合，对涡轮叶片的寿命进行可靠性设计优化，其流程如图10所示。为了进一步提高优化的效率，引入Kriging代理模型[19]减少调用网格模型及有限元模型的次数。具体过程如下：

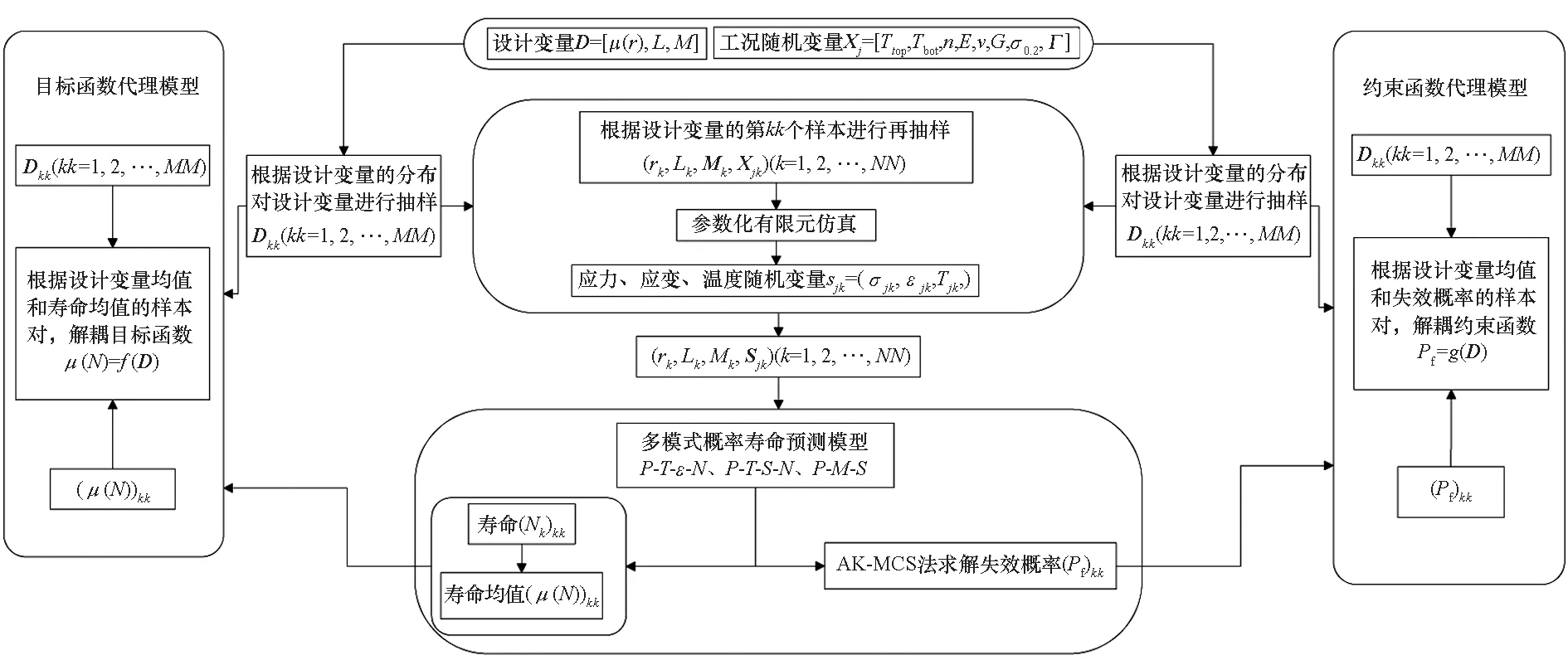
图10 含气膜孔涡轮叶片不确定性多学科设计优化流程Fig.10 Flow chart of reliability-based design optimization for the life of turbine blade with film hole

1)根据所提出的参数化方法，构建参数化的网格模型；

2)对参数化的网格模型加载，进行热力耦合分析以及振动分析，构建参数化的有限元分析模型；

3)根据设计变量以及不确定性变量，生成样本池，选取初始样本点，调用网格模型及有限元模型，将有限元计算结果代入多模式概率寿命预测模型进行寿命估计，分别构建并更新目标函数和约束函数的Kriging代理模型直至收敛；

4)利用解耦法[20]调用Kriging模型进行可靠性设计优化，直至结果收敛。

表11给出了优化前后的设计变量取值对比、寿命可靠度以及均值。优化后气膜孔的半径均值为0.3 mm，相对于初始位置上移0.6 mm，左移0.6 mm；相比优化前的气膜孔几何参数，涡轮叶片的寿命均值提高了10.40%。

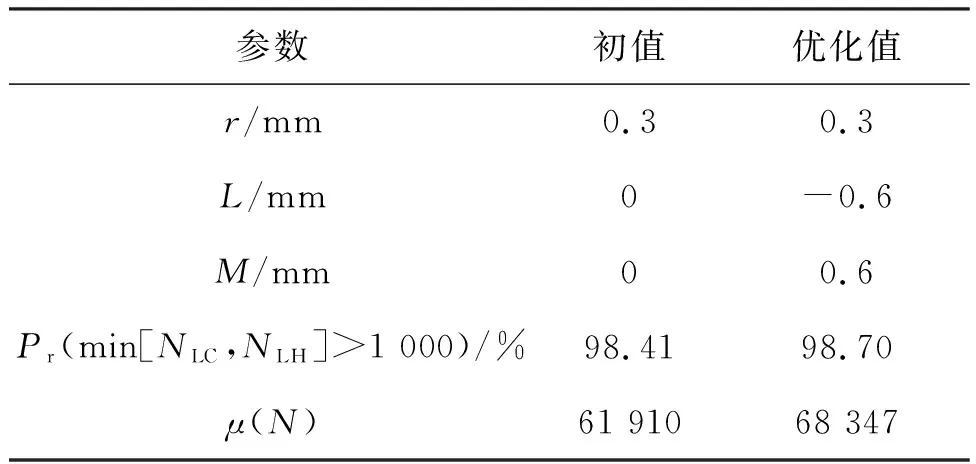
表11 可靠性设计优化结果

在上述优化问题中，由于目标函数与可靠性约束函数的寻优方向一致，即寿命均值增大的寻优方向与可靠性提高的方向一致，因此最优值位于设计变量的几何约束边界，且位于可靠性约束的可行域内部。由于气膜孔的几何参数受到叶片构型的限制，在满足可靠度的约束下，提高寿命均值的最优值位于气膜孔的几何边界。

3 结论

本文提出了含气膜孔涡轮叶片的非结构局部网格参数化方法，该方法通过划分参数化区域和非参数化区域，对涡轮叶片建立局部参数化的网格模型，减少了叶片的网格总数量，从而很大程度上缩减了有限元分析的计算时间，非结构化网格的使用也使得整个画网格的工作时间成本降低。所提方法生成的网格模型质量良好，与结构化网格计算结果一致，能够保证有限元的计算精度。通过该方法可以自动且高效地实现含气膜孔涡轮叶片寿命可靠性设计优化。利用所提网格参数化方法建立网格模型及有限元分析模型，获得不确定性条件下的叶片寿命，通过解耦法对含气膜孔涡轮叶片进行设计优化，使得寿命相比初始几何构型提高10.40%。由于重在实现可靠性设计优化数值仿真过程中的网格参数化过程，对于优化结果与试验结果的对比未做深究。所提方法同样适用于其他复杂几何结构在可靠性优化设计数值计算中的局部优化问题。该局部参数化方法能够保证一定数量的气膜冷却孔结构的网格参数化的效率，随着气膜孔数量的增多，重构网格的耗费时间也随之增加，因此，在优化的气膜孔数量较多时，需要考虑整个网格划分工作的时间成本以及优化过程中网格模型生成的时间成本之间的平衡。