反无人机绳网捕获系统的动力学建模与仿真*
陈青全,丰志伟,张国斌,王 星,张青斌
(国防科技大学 空天科学学院, 湖南 长沙 410073)
无人机技术的发展使得其在生活、工作[1-7]中发挥着愈发重要的作用,无人机具有的体积小、飞行空域低和雷达难以探测等特性[8],使得其可能被不法分子利用从而造成各种破坏,如非法进入敏感空域、贩毒、走私等,给社会稳定带来重大安全隐患,因此反无人机技术成为近几年来世界各国关注的热点研究领域之一[9-12]。
绳网捕获作为一种新兴的反无人机模式,其具有的高容差、低要求和低成本等特性,使其迅速得到发展。按照发射位置的不同分类,反无人机绳网捕获模式分为地面发射捕获和空中发射捕获。地面捕获为地面瞄准和发射,例如英国OpenWorks公司研发出的肩扛式发射器SkyWall。空中捕获是利用装载有绳网的无人机在空中瞄准和发射,捕获目标无人机并运送至指定区域,例如美国密歇根理工大学研制的无人机捕获系统。
尽管各组织研究了各类反无人机绳网捕获武器,但从公开文献上看,对无人机的拦截过程以及拦截之后的回收着陆过程尚无深入和全面的动力学建模,也无较为完整的全过程仿真分析。事实上,国内外对柔性绳网的应用及理论分析主要集中在空间清除太空垃圾方面。如欧空局名为ROGER的地球静止轨道废弃卫星绳网抓捕项目[13-16];美国NASA名为GRASP[17-18]的绳网捕获项目等。动力学研究方面,Gärdsback等[19]建立了空间飞网旋转展开模型,利用商业软件进行了仿真模拟;Hobbs[20]研究了绳索的弹性和疲劳断裂,初步分析了绳索的自接触机理;于洋等[21-23]利用商业软件分析了空间柔性绳网的展开;张青斌等[24-29]研制了地面试验样机,进行了绳网地面试验,并基于离散化模型,研究了空间绳网展开过程的动力学特性,进行了天地差异性分析。
相比于空间碎片捕获任务,地面反无人机绳网捕获任务最大的不同就在于绳网受到不可忽视的重力和空气作用力。在上述力的作用下,绳网的网形变化与在空间环境中的相差甚远。前期的试验和仿真研究表明,重力和空气作用力可能使得绳网不能完全展开,或者提前收拢,导致反无人机抓捕任务失败。因此,有必要进行反无人机绳网捕获任务的全过程动力学分析,并以此指导实际任务。
本文在项目组前期空间绳网和降落伞的研究基础上,结合“低、慢、小”无人机的任务特征,阐述了平台发射、绳网展开以及目标捕获后降落伞回收的无人机捕获过程;建立了捕获平台的六自由度刚体动力学模型;基于离散化的策略,采用绳索有限段的半阻尼弹簧模型分析了绳网展开过程的位置和形状变化特性;采用九自由度物-伞多体动力学模型分析了绳网捕获目标后的坠落过程。然后以某网捕系统为例,进行了全过程的仿真分析,并利用部分飞行试验数据验证校核了模型,研究反无人机绳网捕获过程的特性。
1 无人机捕获过程描述
图1给出了绳网捕获无人机的三个大体阶段:①通过火箭或其他形式动力以一定初速度v0和角度α0发射总质量为m0的捕获平台;②当平台飞行至目标空域时,二次发射绳网抓捕目标;③展开降落伞,完成目标无人机的捕获回收。

图1 无人机捕获过程示意Fig.1 Schematic diagram of the capture process of the UAV
2 动力学建模
分别对捕获平台飞行、绳网展开捕获和降落伞回收进行动力学建模。
2.1 捕获平台飞行动力学建模
采用六自由度刚体模型建立捕获平台的轨迹动力学模型,如图1所示。以地面发射点为原点oD建立右手直角坐标系oD-xDyDzD,其中oDxD轴方向为发射时刻平行于地面且指向目标无人机的方向,oDyD轴垂直大地竖直向上;以捕获平台质心为原点ob建立右手直角坐标系ob-xbybzb,obxb轴沿捕获平台纵轴指向头部,obyb轴在平台纵向对称面内垂直于obxb轴向上;以ob为原点建立右手直角坐标系ob-xvyvzv,obxv轴为沿平台速度方向,obyv轴竖直向上。
捕获平台在飞行过程中,受到重力、气动力和推力作用。不考虑有推力情况,则在不考虑地球自转的情况下,捕获平台质心的动力学方程为
(1)

在ob-xbybzb中建立其绕质心转动的动力学方程为
(2)
其中:ωx、ωy和ωz为捕获平台的角速度,Ix、Iy和Iz为转动惯量,Mq.xt、Mq.yt和Mq.zt为ob-xbybzb中的气动力矩分量。联立式(1)和式(2)即可求解平台的运动特性。
2.2 绳网发射展开动力学建模
采用质量块牵引的方式展开绳网,装置如图2所示。发射时抛掉前罩,质量块以发射速度vnet和角度βnet牵引展开绳网。

图2 绳网发射装置示意Fig.2 Schematic diagram of the tethered-net launching device
在柔性绳网多体动力学模型的基础之上,考虑重力和空气阻力的影响,建立低空条件下绳网展开过程的动力学模型[26-29]。如图3所示,采用离散化的建模思路,将绳网划分为若干绳段,各绳段可受拉不可受压,质量集中于两端点。

图3 绳网的“半弹簧阻尼”模型Fig.3 Semi-spring damper model of the tethered-net
绳段单元sij的内力方向沿着单元径向,大小近似为线弹性与线性阻尼之和,即
(3)
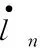
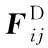
(4)

图4 绳段sij所受外力Fig.4 External force acting on the segment sij
考虑绳索的透气性,采用Paul Williams[28]经验公式得到阻力系数CD和升力系数CL分别为
CD≈0.022+1.1sin3αn
(5)
CL≈1.1sin2αncosαn
(6)
其中,αn为绳段的攻角,其余弦cosαn可以表示为
(7)
(8)
(9)
其中,ρair为空气密度,d为绳子的直径,eD和eL分别为空气阻力和空气升力的单位方向向量。
(10)
(11)
根据牛顿第二定律,节点i的动力学方程可以表示为
(12)

(13)
(14)
(15)
(16)
其中,R(i)为与节点i存在连接关系的节点集合。
初始时刻绳网折叠封贮于网舱内,但是由于相关的弹射展开过程十分复杂,需另行详细论述。结合前期试验与仿真结果,为简单起见,假定绳网初始状态为原绳网的等比例缩小版,且不考虑网舱对绳网的作用。
2.3 捕获后的无人机-降落伞动力学模型
绳网抓捕目标无人机后,降落伞拉出回收。为了简化问题,忽略绳网碰撞过程和降落伞充气过程。
参考文献[29-30],本节建立如图5所示的九自由度多体动力学模型,其中oc为物-伞铰接点。以oc为原点建立固连的右手直角坐标系oc-xpypzp和oc-xtytzt,ocxp轴沿降落伞对称轴向下,ocxt轴定义为降落伞展开时刻网和无人机组合体过oc竖直向下的体轴。参考文献[31-32],得到物-伞九自由度力学方程为

(17)
(18)
(19)


图5 物-伞多体系统示意Fig.5 Parachute-payload multi-body system
3 仿真与试验分析
对平台飞行、绳网捕获和降落伞回收全过程进行数值仿真分析,并基于试验数据,分别对平台飞行和绳网展开模型进行验证。
3.1 试验及仿真工况
结合网捕系统试验,令质量为5 kg的无人机以40 km/h的速度平行于发射坐标系oDxD轴飞行,主要参数见表1。

表1 主要系统参数
3.2 结果与分析
图6为捕获平台的飞行仿真结果与试验数据对比图。图中曲线吻合较好,最大的高度偏差约为17.2 m,对应偏差百分比约为4.6%,满足工程任务要求,验证了捕获平台仿真模型的有效性。

图6 捕获平台飞行轨道试验与仿真结果对比Fig.6 Comparison of test and simulation results of the flight path of the platform
图7为绳网发射展开过程中网口直径的仿真结果与高速图像试验测量数据对比图。图8为仿真得到的部分时刻绳网形状变化图。从图7中可以看出,试验与仿真的网口直径随时间的变化较为符合。且从图8中可以看出,仿真中绳网先呈束状牵引随后网面迅速展开,通过定性地对比试验图像,吻合度较好,这验证了绳网展开动力学模型的有效性。

图7 网口直径的试验与仿真结果对比图Fig.7 Comparison of the test and the of the diagonal length simulation results

(a) 0.03 s
忽略降落伞与绳网-无人机组合体的碰撞和碰撞之后的平衡过程,由动量定理计算得到状态平衡之后的系统速度约为0.9 m/s,俯仰角约为83.3°。由于试验测量条件限制,未能收集得到系统下落过程数据。
图9为无人机捕获全过程高度随相对飞行时间的变化图。第一阶段,捕获平台以v0=100 m/s 和α0=73°的初始条件从地面发射,经过9.0 s飞行后升高到约435.1 m,此时捕获平台的俯仰角约为6.5°,速度约为27.3 m/s;第二阶段,绳网质量块以vnet=70 m/s 和βnet=40° 初始条件发射,在绳网展开过程中,向前飞行了约4.8 m,向上飞行了约0.5 m;第三阶段,降落伞-绳网-无人机系统的下落时间约为69.4 s,着陆速度约为7.2 m/s[33]。

图9 系统运动过程飞行高度随时间的变化Fig.9 Flight altitude variation with time during system motion process
4 结论
本文针对无人机“黑飞”问题,基于项目组空间绳网和降落伞研究基础,结合无人机“低、慢、小”等特点:提出了一种基于无人机绳网抓捕和降落伞回收的总体方案;建立了捕获平台的六自由度刚体动力学模型、绳网有限段的半阻尼弹簧模型和九自由度的降落伞-绳网-无人机动力学模型;进行全过程仿真,并通过部分系统试验,对模型进行了验证。仿真结果表明,绳网无人机捕获系统方案可行,动力学模型有效。为绳网无人机捕获系统的设计提供了理论依据。

