亚音速轴流风扇静转子相互作用线谱噪声预报*
武星宇,魏应三,靳栓宝,王 东,祝 昊,胡鹏飞,孙方旭
(海军工程大学 舰船综合电力技术国防科技重点试验室, 湖北 武汉 430033)
轴流风扇被广泛应用于民用和军用航空领域,例如涡扇发动机,其低噪声设计一直以来都受到国内外许多学者的关注和研究[1]。从频谱上看,风扇气动噪声包含线谱噪声和宽带噪声。其中,宽带噪声源于风扇静转子叶片与随机湍流脉动的相互作用,线谱噪声主要源于周期性转子尾流与下游静子的相互作用[2-3]。对于大涵道比航空发动机,线谱噪声为其主要噪声源,因此深入研究转子尾流与下游静子相互作用产生的线谱噪声对抑制风扇噪声具有重要意义。
随着计算机技术的快速发展,数值分析法开始广泛用于轴流机械非定常气动特性和噪声机理的研究,Verdon等[4]通过数值法求解三维线性欧拉方程,得到轴流涡轮机械静子叶栅叶频和倍叶频下叶片表面非定常脉动压力的分布。Elhadidi等[5]采用线性的欧拉方程和片条理论,计算分析了叶片弯掠设计对风扇线谱噪声的影响。为考虑流体黏性和静子对转子尾流的影响,Rumsey等[6]通过数值法求解非定常雷诺平均N-S方程,计算分析了风扇静转子相互作用噪声。Grace等[7]通过三维非定常雷诺平均N-S方程模拟计算静子表面的非定常压力,并据此预测叶栅出口线谱辐射声功率。通过数值法可较准确地预报轴流风扇的气动噪声[8-9],但数值法建模时间和计算时间较长,在风扇初期选型与参数设计时不适宜采用数值法。相对于数值计算方法,解析法在计算时间上具有很大的优势,适用于风扇初期的低噪声设计。
通过升力面理论计算流场与风扇叶片相互作用产生的表面压力脉动,结合声类比方程可进一步计算得到风扇的辐射噪声。张伟光等[10]利用三维升力面理论计算转子尾流与静子叶片相互作用产生的线谱噪声,并分析叶片弯掠设计对风扇线谱噪声的影响,但是升力面理论不能考虑风扇静子的安装角[11]。为此,Carazo等[12]采用数值法模拟转子尾流,结合Amiet[13]叶片非定常响应理论模型,计算得到对转螺旋桨线谱声压值,计算结果与试验结果相近,但是该模型未考虑叶片之间的相互作用。Posson等[14]在Glegg[15]叶栅响应函数的基础上,推导得到叶片表面压力脉动分布解析表达式。在此基础上,de Laborderie等[16-17]推导出风扇线谱噪声计算公式,结合试验得到的转子叶片尾流参数,得到的风扇辐射声功率级计算值与试验值在一倍叶频处相近。此外,Rozenberg[18]、Sanjosé[19]、Magne[20]等也采用解析的叶栅非定常响应模型计算风扇线谱噪声,但上述研究需要先计算叶片的非定常响应,然后通过声类比方程计算风扇辐射噪声,且需要数值法或试验法提供的转子尾流场参数。Philbrick等[21]试验测量了叶片尾流参数,拟合曲线得到叶片经验尾流模型,并通过该模型预报风扇线谱噪声,发现采用试验尾流数据和采用经验尾流模型得到的风扇线谱噪声结果相近。
本文将针对风扇静转子叶栅相互作用线谱辐射噪声进行研究。在文献[15]中的简谐湍流波作用下叶栅散射场速度势解析表达式的基础上,考虑风扇转子尾流的作用,通过傅里叶分解将转子尾流分解为若干简谐湍流波的叠加[21],从而推导得到转子尾流作用下静子叶栅散射场的速度势计算表达式,通过声强与速度势以及辐射声功率与声强的关系进一步推导得到了静子叶栅线谱噪声计算公式,并通过与NASA风扇试验模型和后掠、倾斜静子升力面计算模型对比验证了该公式的适用范围。并在此基础上分析静转子间距、静子叶片参数等对风扇线谱噪声的影响。
1 叶栅线谱噪声公式推导
1.1 转子叶栅尾流模型
忽略叶片厚度,在半径r处截取风扇静转子叶片并展开,可得到如图1所示的静转子叶栅。图1中:Ω为转子的转速,Sr为转子叶栅栅距,αr为转子叶栅安装角,L为转子尾流半尾迹宽度,DS为转子后缘流向距离,(x,y)为固定在转子叶栅上的坐标系;αs为静子叶栅的安装角,(xs,ys)为固定在静子叶栅上的坐标系。

图1 静转子叶栅示意Fig.1 Schematic diagram of stator and rotor cascades
大量试验表明,单个叶片尾流可用高斯分布描述,在图1中的o-xy坐标系下其表达式[21-23]为
(1)
式中,w0(x,y)为叶片尾流场速度梯度分布,wr为转子中心尾迹区轴向速度亏损。
对于转子叶栅,转子尾流场为单个叶片尾流场的叠加,即
(2)
式中,wR(x,y)为转子尾流场速度梯度分布,表示的是转子尾流场中某位置的流速与平均流速的差值,Z为整数。
以T=Srcosαr为周期将式(2)傅里叶级数展开,得
(3)
式中,xr·nr=ycosαr+xsinαr,F为xr·nr的函数。
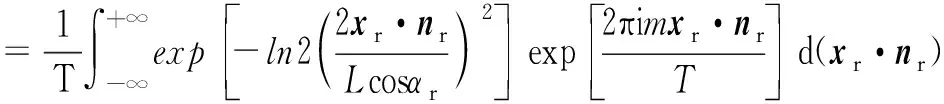
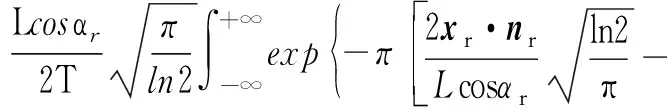
(4)

(5)
由于式(4)中的半尾迹宽度L与DS有关,为此F可改写为F′(DS)。 结合式(3)得到

Philbrick等[21]给出转子中心尾迹区轴向速度亏损wr和半尾迹宽L经验计算公式。
(6)
(7)
其中:W0为转子尾流平均速度;cr为转子叶片弦长;Cd为转子叶片阻尼系数,根据经验[21]有
(8)
式中,κ为叶片稠度,α1为进口相对气流角,α2为出口相对气流角,λ为压力损失系数。
考虑转子与静子坐标变换,在y方向上有
ys=y+Ωrt
(9)
得到周期性转子尾流垂直于静子叶栅的速度分量为

(10)
式中,B为转子叶片数。
1.2 叶栅线谱辐射声功率
Glegg[15]针对图2所示叶栅模型提出叶栅响应函数理论,该理论通过Wiener-Holf方法求解叶栅散射场速度势函数积分表达式,最后得到简谐湍流脉动作用下叶栅散射场的速度势函数解析表达式,推导得到的表达式可由式(11)表示。
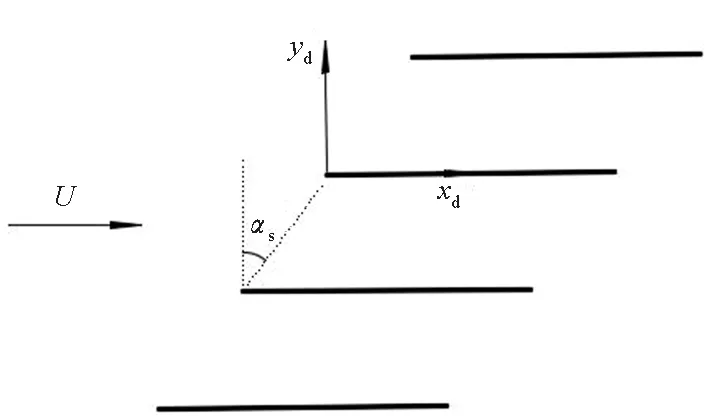
图2 平面叶栅结构示意Fig.2 Schematic diagram of plane cascade structure

ikzzd-iωt]
(11)

通过片条理论,在半径r处截取环形风扇中Δr段,假设在分段内的流体入流参数一致[16],考虑叶栅入流为转子尾流,叶栅的速度势函数解析表达式可改写为
i(σ-2πq)yd/h+ikzzd-imBΩt]
(12)
声强与速度势的关系[15]为
(13)
式中,“*”表示共轭,I为声强。
代入速度势函数,可得到

(14)

辐射声功率Π与声强的关系[15]为
(15)
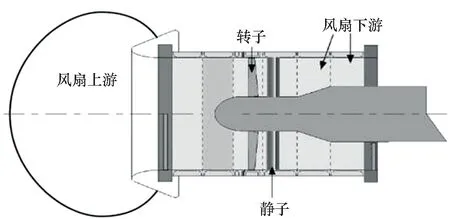
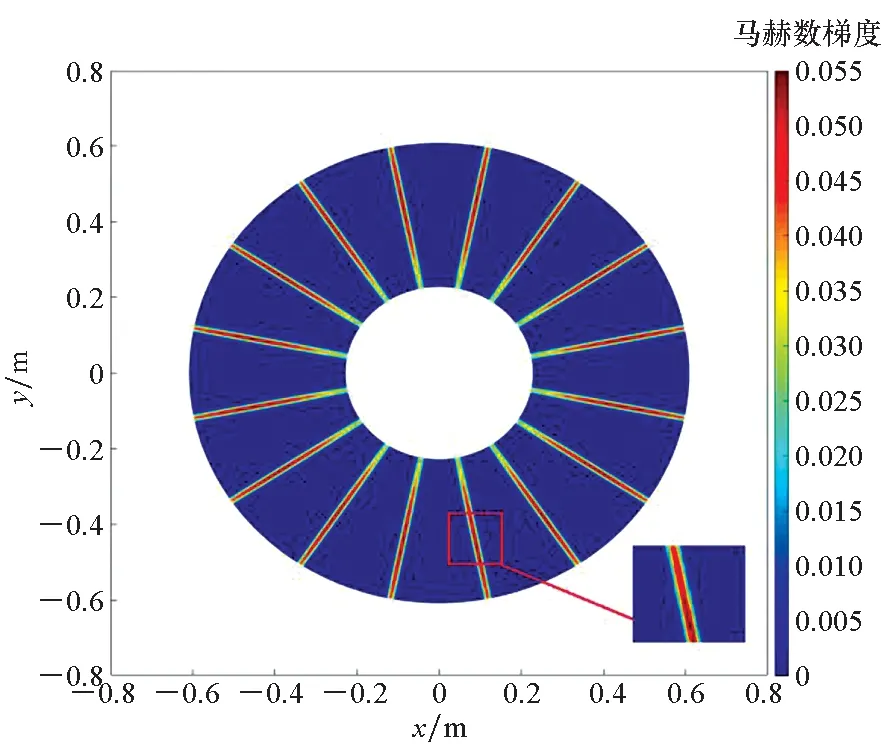
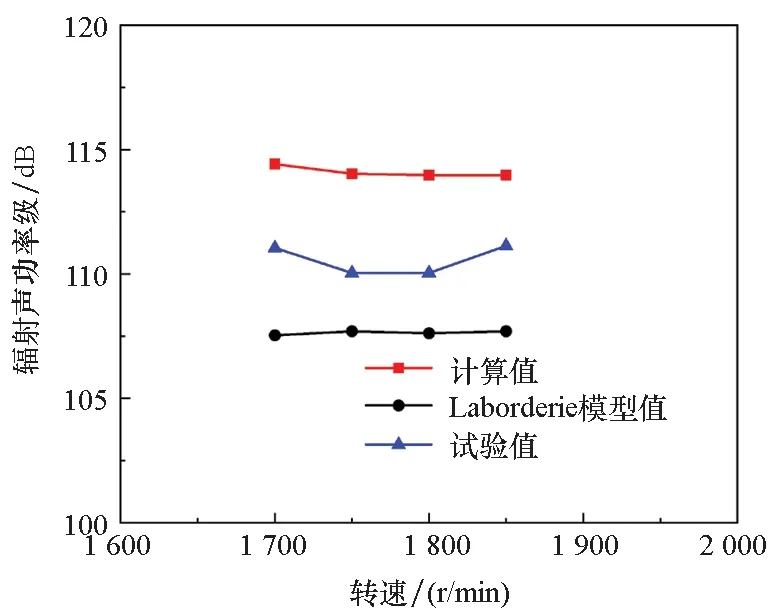
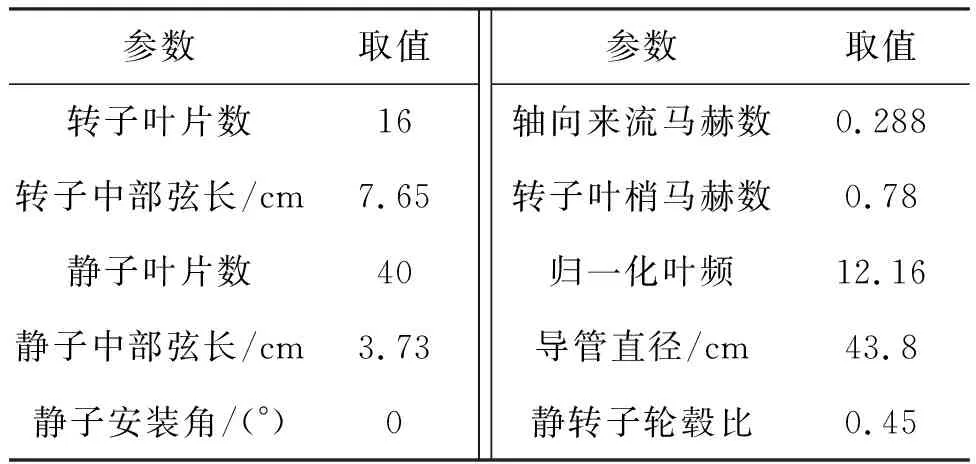
对于图1所示的叶栅结构,其积分曲面定义在曲线x-yd/h=const和r (16) 式中,Re表示取实部,这是由于辐射声功率为实数时才能辐射出来。 通过式(16)可得到静子第m阶辐射声功率计算表达式,即 (17) 相邻叶片间湍流相位差角σ=kxdd+kydh,其中kxd为Glegg坐标系下的轴向波数,kyd为侧向波数。不考虑叶片后掠和倾斜,波数在Glegg坐标系od-xdyd与坐标系os-xsys之间的转换关系[16]为 (18) 图3为后掠和倾斜叶片示意图。图3(a)中φ为后掠角,可表示为沿叶片径向的函数φ(z)。图3(b)中ψ为后掠角,可表示为沿叶片径向的函数ψ(z)。此时固定在静子叶片前缘的坐标系os-xsyszs与Glegg坐标系od-xdydzd之间的转换关系如式(19)所示。 (a) 后掠(a) Swept (b) 倾斜(b) Lean图3 后掠与倾斜叶片示意Fig.3 Schematic diagram of swept and lean blade (xd,yd,zd)T=Q×(xs,ys,zs)T (19) 式中,Q为转换矩阵,其定义[16]为 (20) 通过Q可得到坐标系od-xdydzd下的叶栅入流参数。 (21) 其中,[U0,Uyd,Uzd]T为od-xdydzd坐标下的入流速度,[Uxs,Uys,Uzs]T为os-xsyszs坐标下的入流速度,kzd为od-xdydzd坐标下z向入流波数,kzs为os-xsyszs坐标下z向入流波数。静子叶栅来流波数K=[kxs,kys,kzs]T与流速U=[Uxs,Uys,Uzs]T满足如式(22)所示关系[16]。 K·U=mBΩ (22) 考虑叶片在zs方向上波数的变化,在坐标系os-xsyszs下的波数为 (23) 其中,p为整数,Rt为叶梢半径,Rh为轮毂半径。通过式(21)可得到Glegg定义坐标系下的叶栅入流参数。此外,由于倾斜和后掠角的影响,静子在Glegg坐标系下的弦长c、垂向间距h和轴向间距d也发生了变化。 (24) 其中,cs为os-xsyszs坐标系下的弦长,Ss为静子叶栅栅距。 NASA[22]在半消声室中测量了不同转速和静子叶片数下风扇的线谱噪声,其试验模型如图4所示,主要参数如表1所示。试验测量了转子转速分别为1 700 r/min,1 750 r/min,1 800 r/min,1 850 r/min和1 887 r/min时的风扇线谱噪声,在转速为1 800 r/min时,转子叶片叶梢马赫数为0.34,轴向马赫数为0.15。 图4 NASA试验风扇结构[22]Fig. 4 NASA′s fan test structure[22] 表1 NASA风扇试验参数 Sutliff等[24]给出了转子流场参数试验测量结果,通过转子入流流速,图5给出了转速为1 850 r/min时的转子尾流场马赫数梯度经验公式计算云图。通过经验公式计算得到,在叶片中部转子尾流中心线速度亏损约为18 m/s,Sutliff试验测量的结果约为20 m/s,经验结果与试验结果相近。 图5 周期性转子经验尾流公式计算云图Fig.5 Cloud diagram of periodic rotor wake by empirical 假设导管壁面为硬壁面,即不考虑导管的吸声作用,通过式(17)即可得到风扇静子的线谱辐射声功率。图6、图7分别给出13叶静子和14叶静子的线谱辐射声功率级(参考声压级为10-12W)试验值与计算值对比曲线图,计算值包括本文公式计算值与Laborderie[16]模型计算值,式(18)中的m=1时可得到叶频处的辐射声功率,m=2时可得2倍叶频处的辐射声功率。图6(a)与图6(b)分别为叶频处风扇上游和下游线谱辐射声功率级,图6(c)与图6(d)分别为风扇上游和下游2倍叶频处线谱辐射声功率级。 (a) 风扇上游辐射声功率级(叶频)(a) Sound power level of the fan′s upstream in BPF 通过图6可得,当静子叶片数为13、转子转速为1 700~1 887 r/min范围时,在叶频处本文公式计算得到的风扇线谱辐射声功率级与试验值相差2~4 dB,特别是在叶频下游工况,本文公式计算结果与试验值相近。 通过图7对比14叶静子的线谱辐射声功率级可得,在叶频下游本文公式计算得到的辐射声功率级与试验值相差3 dB以内;但是在2倍叶频处,计算值与试验值相差较大,接近10 dB。总体而言,在上述计算工况,相比于Laborderie模型,本文公式在叶频下游处的预报结果与试验值更加接近,但是在2倍的叶频处,本文的计算结果偏大,这是由于使用经验模型预报转子尾流参数时时未考虑转子尾流沿静子弦长的变化,导致傅里叶分解后2倍叶频处的速度梯度偏大;而在叶频处,本身速度梯度基数较大,弦长对转子尾流速度梯度的影响较小。 (a) 风扇上游辐射声功率级(叶频)(a) Sound power level of the fan′s upstream in BPF Schulten[25]采用升力面法分析了后掠叶片对风扇线谱噪声的影响,模型参数如表2所示。 表2 Schulten后掠静子风扇模型主要参数 表2中,归一化叶频为转子叶梢马赫数与转子叶片数的乘积。此外,转子阻尼系数为0.01,静转子间距在叶中位置保持2.6倍的静子弦长。在采用经验公式计算转子尾流参数时,考虑后掠角导致的静转子间距的变化。图8给出静子的线谱辐射声功率级本文公式计算值与Schulten升力面理论计算值对比曲线图,由于风扇叶频噪声被截止,因此图中计算频率为2倍的叶片通过频率。 由图8可得,在当后掠角小于8°时,本文公式计算得到的辐射声功率与Schulten升力面计算模型计算得到的辐射声功率相近,但是当后掠角大于8°时,本文公式计算得到的辐射声功率快速下降,与Schulten计算模型得到的结果相差较大。这是由于本文公式基于平面叶栅推导而来,在大后掠角下,轴向波数变小,叶栅部分模态的辐射噪声被“截止”,但对于环形叶栅,在平面叶栅中被“截止”的辐射模态不一定会在环形叶栅中被“截止”,这导致本文计算得到的结果与Schulten计算得到的结果相差较大。 (a) 静子上游辐射声功率(a) Sound power level of the stator′s upstream 张伟光等[10]采用升力面法分析了倾斜角对风扇线谱噪声的影响,计算参数如表3所示,其中弦长与静转子间距参数通过导管直径做归一化处理,导管直径为0.4 m。 表3 Schulten倾斜静子风扇模型主要参数 图9给出静子线谱辐射声功率级本文公式计算值与文献[10]升力面理论计算值对比曲线图,计算频率为1倍的叶片通过频率,其中纵坐标为计算结果与上游0°倾斜角的辐射声级计算结果相对值。 (a) 静子上游辐射声功率(a) Sound power level of the stator′s upstream 由图9可得,当倾斜角在0°~10°范围内变化时,本文公式计算值与升力面计算值相差5 dB以内,且两者发展趋势一致。对于上述模型,叶片的倾斜设计反而使静子的线谱噪声变大。 在2.1节NASA 13叶静子风扇试验模型的基础上,图10给出了静转子间距、静子弦长、静子倾斜角和静子叶片数等参数变化对静子辐射噪声的影响。 (a) 静转子间距的影响(a) Influence of the stator-rotor space 考虑到下游叶频噪声为主要噪声贡献量,图10计算的均是下游叶频噪声,图10(a)为静转子间距变化对静子线谱噪声的影响曲线图,由图可得,静转子间距对静子线谱噪声影响较大,随着静转子间距增大,风扇线谱噪声降低,但同时降低的幅值越来越小。 图10(b)为弦长变化对静子线谱噪声的影响曲线图,由图可得,弦长变化对NASA试验模型的线谱噪声影响较小。 图10(c)为倾斜角变化对静子线谱噪声的影响曲线图,由图可得,当倾斜角小于4°时,风扇线谱噪声变化较小,当倾斜角大于4°时,倾斜角越大,风扇线谱噪声越小。 图10(d)为叶片数变化对静子线谱噪声的影响图,由图可得,15叶静子的线谱噪声最小,其次是17静子,20叶静子的线谱噪声最大。此外,在图10(d)中16叶静子由于与转子叶片数相等,导致计算中出现奇点;当叶片数大于21时,叶频噪声被“截止”。 本文在叶栅响应函数的基础上推导了风扇静转子相互作用线谱辐射声功率预报公式,通过转子经验尾流模型为该公式提供入流参数,并考虑静子叶片后掠和倾斜设计对线谱噪声的影响。通过与NASA试验模型和升力面计算模型对比,验证了本文公式适用性和适用范围,得到如下结论: 1)本文公式能够较准确地预报风扇线谱噪声,但是本文公式不适用于后掠叶片线谱噪声的计算,这是因为平面叶栅中被“截止”的声辐射模态在环形叶栅中不一定会被“截止”。 2)叶片的倾斜设计并非都能抑制线谱噪声,对于部分模型叶片的倾斜设计反而会增大线谱噪声。 3)针对NASA风扇试验模型,增大静转子间距和倾斜设计能够抑制线谱噪声,但是静子叶片弦长对线谱噪声影响很小;此外,叶片数对风扇的线谱噪声影响较大,特别是可通过增加叶片数的方式来“截止”静子叶频噪声。因此,合理的静转子叶片数匹配设计对风扇噪声被动抑制具有重要意义。 综上所述,本文解析公式可预报风扇静转子相互作用线谱噪声,相对于常用的数值法,在计算时间上具有一定的优势,适用于风扇叶片的初期选型和低噪声设计。与升力面理论相比,本文公式直接通过速度势函数计算得到风扇线谱噪声,无须先求解叶片表面的非定常压力脉动,其物理意义更加清晰,计算过程更加简单。此外,升力面法无法考虑安装角的影响。本文公式则可考虑安装角和倾斜角对风扇线谱噪声的影响,但是也存在一定的缺陷,对于后掠角过大的模型其预报结果不是很准确,还需要进一步优化本文公式。 致谢 清华大学黄振卫博士和海军潜艇学院段嘉希博士在数据处理提供了帮助和指导,谨致谢意!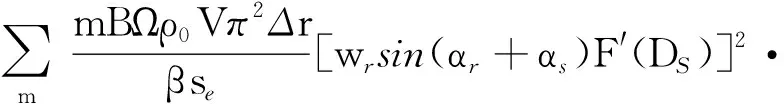
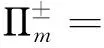

1.3 叶片后掠和倾斜的影响

2 结果和讨论
2.1 不考虑叶片后掠与倾斜


2.2 考虑叶片后掠

2.3 考虑叶片倾斜


3 参数影响分析

4 结论

