双高速摄像机交汇的高旋弹丸位姿估计算法及误差分析*
杨志伟,王良明,张喜峰,王 垚
(1. 南京理工大学 能源与动力工程学院, 江苏 南京 210094; 2. 北方华安工业集团有限公司, 黑龙江 齐齐哈尔 161046)
弹丸的炮口信息(如初速、跳角、起始攻角等)对研究弹丸飞行稳定性、初始扰动和着靶姿态等方面都有着十分重要的意义[1]。尾翼稳定弹丸在外弹道上的速度、飞行轨迹可由弹道雷达测得,姿态则可借助于一些弹载传感器测得[2]。然而对于高旋弹丸,由于其膛内大过载、膛外高转速的复杂弹道环境,很多传感器在炮口处甚至全弹道上都无法正常工作。所以高旋弹丸的炮口信息测量一直是一项意义重大且充满挑战的课题。
基于电荷耦合器件(Charge Coupled Device, CCD)的测量技术是一种非接触式的测量技术,很早便运用于靶场测量弹丸的飞行姿态。姜寿山等[3]采用多镜头方案,解决了早期线阵CCD扫描速度不够的问题,理论上给出了一种弹丸姿态测量方法。高昕等[4]、王小力[5]和孙磊[6]均基于双CCD交汇测量系统,先后提出了弹丸炮口处章动角测量方法和CCD弹丸图像抗干扰处理方法。利用弹丸穿过纸靶后留下的弹孔信息进行弹丸姿态测量也是靶场常用的一种测量方法。文献[7]和文献[8]分别给出了这种测量方法的原理和数据处理方法。赵竹新等[9]提出了基于线阵摄像机的数字狭缝摄像技术,克服了传统胶片式狭缝摄影技术的缺点,通过试验获得了弹丸速度和攻角。总结以上弹丸姿态测量方法发现,这些方法数据量少,难以描述弹丸周期性的章动和进动。王宝元等[10]提出了基于弹道跟踪原理的弹丸姿态测量方法,可以测量一段时间内连续的弹丸姿态。然而该方法受测量原理和设备的约束,目前只能用于平射弹丸姿态测量,且忽略了弹丸的进动运动,测量误差较大。
受益于近年来高速摄像技术的发展,无论是采用高速CCD摄像头,还是高速互补金属氧化物半导体[11](Complementary Metal Oxide Semiconductor,CMOS)摄像管为探测器件的高速摄像机,都能拍摄到高频率、高像素的弹丸运动视频。弹丸的位置和姿态测量似乎可以简化成基于图像的物体位姿估计问题,其实不然。图像位姿处理方法分为两种,一种是基于2D像素图像的位姿估计方法,另一种是基于3D深度图像的位姿估计方法[12]。为了满足大射角、高初速的测量需求,需要尽可能长时间地记录弹丸的运动,所以摄像机的架设位置必需远离弹道线。这样一来,弹体表面的深度差异就可忽略,基于3D深度图像的位姿估计方法就无法使用。此外,很多基于2D像素图像的位姿估计方法需要物体的纹理清晰[13]或是几何特征明显。然而旋转弹丸是旋成体,不同于尾翼稳定弹丸,几何特征较弱。弹丸在炮膛内会受到火药气体的烧蚀和冲刷,表面纹理也会发生改变。所以基于2D像素图像的位姿估计方法也很难获得理想的结果。观察所拍摄的弹丸图像可知,除有以上各类缺点外,弹丸图像的轮廓也有着不同程度的缺失。
虽然存在着各种不足,但是弹丸的轴线可根据两条平行边线和弹丸顶点准确提取。因此本文利用弹丸图像的这一特点,结合高旋弹丸在炮口处的弹道特性,提出一种基于双高速摄像机交汇测量方法的位姿估计算法,并进行了误差分析。将所提取的信息与其他测量设备的测量结果进行比较,验证了该位姿估计算法的测量精度,为靶场测试、验收等工作提供了一种高精度的炮口信息测量方法。
1 测量方法设计
1.1 坐标系介绍
为了便于描述真实弹丸和图像中弹丸之间的关系,不仅要用到一些弹道所必需的坐标系,还需要引入一些和图像表示相关的坐标系。
图像坐标系OFxFyF是一个二维平面坐标系,以像素点为单位,坐标原点在图像的左上角,OFxF和OFyF轴的指向如图1所示。

图1 图像坐标系和摄像机坐标系Fig.1 Figure coordinate system and camera coordinate system
摄像机坐标系OMxMyMzM的原点在屏幕的中心,OMxM和OMyM轴分别与图像坐标系的OFxF和OFyF平行,OMzM轴由右手定则确定。根据该定义可知,摄像机坐标系的OMzM轴和摄像机的光轴重合。
由摄像机坐标系中的点(xM,yM,zM)转化到图像坐标系中的坐标(xF,yF),其转化关系式为
(1)
其中
(2)
式中,Nx、Ny分别表示图像在OFxF和OFyF方向上的像素点数,L和H分别表示图像的物理长度和宽度,u0、v0表示屏幕平面中心点坐标,fx、fy分别表示在OFxF和OFyF方向上的摄像机焦距。经过标定后的fx、fy应该是相等的,且与摄像机的给定焦距f相等,故本文取fx=fy=f=zM。
由式(1)可知,若获得了某点在一张图像上的像素坐标(xF,yF)和摄像机的全部参数,则可以得到摄像机坐标系中的一条直线。如果有两台摄像机,那么根据两条直线求出交点就能获得点在摄像机坐标系中的值,这样两台摄像机就组成了一个测量系统。
测量系统坐标系ONxNyNzN的原点在任意一台高速摄像机屏幕的中心,ONxN轴为两台高速摄像机屏幕中心的连线且在水平面内,ONzN轴在竖直平面内朝上,ONyN轴由右手定则确定。本文定义,沿射击方向看,布置在射击平面左侧的高速摄像机屏幕中心为测量系统坐标系的原点,如图2所示。

图2 测量系统坐标系Fig.2 Measurement system coordinate system
弹丸的空间位置由弹丸质心在地面坐标系O1xyz中的坐标来描述。弹丸的姿态由弹轴与基准坐标系之间的两个欧拉角(弹轴高低角、弹轴方向角)描述。因为弹丸为旋成体,本文对滚转角不做描述。速度矢量由速度大小和速度轴与基准坐标系之间的两个欧拉角(速度高低角、速度方向角)来描述。弹轴与速度矢量之间的关系直接由二者之间的夹角描述,即总攻角δ,亦可称为章动角。
另外,本文还需用到一些外弹道中常用的坐标系和角度定义。地面坐标系O1xyz,原点在炮口断面中心,O1x轴沿水平线指向射击方向,O1y轴垂直向上,O1z轴可由右手定则确定。基准坐标系与地面坐标系完全平行,原点在弹丸质心,随质心一起平动。弹轴高低角和速度高低角分别为弹轴和速度轴在基准坐标系Oxy面内的投影与Ox轴之间的夹角,弹轴方向角和速度方向角分别为弹轴和速度轴与基准坐标系Oxy面之间的夹角。
1.2 测量原理介绍
如图3所示,两台高速摄像机布置在射击平面两侧,高速摄像机的光轴相交于射击平面,且光轴所组成的平面与射击平面垂直。其中,θ为射角,Lx为高速摄像机光轴交点相对于炮口的水平距离,h为高速摄像机光轴交点相对于炮口的高度,L1和L2均为高速摄像机与射击面的距离,α1和α2均为高速摄像机的高低角。

图3 测量原理示意Fig.3 Measurement principle diagram
图4表示双高速摄像机交汇测量系统的有效视场。四边形ABCD表示有效视场在沿射击方向上的截面。

图4 测量系统有效视场示意Fig.4 Effective viewing field of measurement system diagram
当弹丸通过有效视场区域时,分别在两个高速摄像机的图像平面上留下一系列的图像,根据这些图像和已知的几何关系就能提取弹丸的各种信息。
2 弹丸位姿估计算法
2.1 POSIT算法
POSIT(pose from orthography and scaling with iteration)是1992年首次被提出的、利用物体的二维图像计算物体姿态和位置坐标的一种算法。该算法基于“弱透视近似”假设,即物体距离摄像机足够远时,可以忽略物体内部各点的深度差异[14]。由前文可知,弹丸的图像满足该假设。
POSIT算法要求在物体表面至少找到4个非共面点,利用这4个点在二维图像上的像素坐标经过正交投影和尺寸变化提取姿态。对于已经给定参数的摄像机,可求取物体的透视缩放比例,从而获得物体的近似姿态和位置。然而,这样计算的精度并不高。如果真实的三维物体位于通过前面所算得的近似位置,可以将4个点投影到预期的位置上,再用这些新的像素坐标重新运行算法。如此反复迭代,四五次后算法便可收敛到真实的物体姿态。因此,POSIT算法也被称为“迭代POS”算法。
POSIT算法基于单张图像就能估计出弹丸的姿态和位置,方法简单但也存在缺点。该算法的缺点就在于4个非共面点的选取。弹丸在出炮口时处于高速、高旋转的动态环境中,高速摄像机能否捕捉到这4个非共面的标记点将是一大问题。因为算法要满足“弱透视近似”假设,所以弹丸的图像肯定很小,这样4个标记点的提取也会是一大难题。
开源代码OpenCV中提供了实现POSIT算法的全部代码,并且代码允许跟踪4个以上的非共面点,从而提高姿态估计的精度。
2.2 双高速摄像交汇算法
2.2.1 质心运动轨迹和初速估计计算
选取一侧高速摄像机的视频,逐帧转化为图像格式。将图像中的弹丸提取轮廓并拼接在一张图中。对另一侧的图像进行相同操作,并保证所选取的两侧图像是同一时刻的图像。图5为一侧图像拼接后的结果。

图5 弹丸图像拼接Fig.5 Image splice of projectile
根据弹丸静测结果,确定弹丸质心所在位置,再按比例投影至所绘制的弹丸轴线上去,这样就获得了弹丸质心的像素坐标。两个像素坐标的连线就是速度矢量在该侧图像平面上的投影,也是弹丸质心运动轨迹在该侧图像平面上的投影。
如图6所示,在同一时刻,弹丸质心在两侧图像坐标系内的像素点值分别为P1(x1,y1) 和P2(x2,y2)。根据式(1)将两点分别转化到各自摄像机坐标系中,即PM1(xM1,yM1,f)和PM2(xM2,yM2,f)。由于直线PP1和PP2都经过各自摄像机坐标系的原点,那么可分别求出两条直线在各自摄像机坐标系下的表达式。将两条直线的表达式都转化到测量系统坐标系内,联立求解便可获得质心在测量系统坐标系中的值。

图6 点在图像坐标中的投影Fig.6 Projection of point in picture coordinate system
直线PP1和PP2都经过各自摄像机坐标系的原点,其在各自摄像机坐标系的表达式为
(3)
式中,a、b、c为直线方程的待定参数,根据前文叙述可知c=f,a、b的值可由点P在摄像机坐标系中的坐标PM(xM,yM,f)确定。
根据两台高速摄像机的布置关系,在射击平面左侧的摄像机坐标系先绕OMxM轴逆时针旋转π/2-α1角度,再绕OMzM轴逆时针旋转π/2角度,就与测量系统坐标系重合,二者之间的转化关系为
(4)
对于在射击平面右侧的摄像机坐标系,先绕OMxM轴逆时针旋转π/2-α2角度,再绕OMzM轴顺时针旋转π/2角度,最后向OMxM轴平移L1+L2距离就与测量系统坐标系重合,二者之间的转化关系为
(5)
测量系统坐标系先绕ONzN轴逆时针旋转π/2角度,再绕ONxN轴逆时针旋转π/2角度,再沿ONzN轴正向平移L1距离,沿ONxN轴负向平移Lx距离,就可与弹道中的地面坐标系O1xyz重合,二者之间的转化关系为
(6)
这样就可由图像上的两点像素坐标获得弹丸质心在地面坐标系中的坐标值。将所有的弹丸质心连接起来,就获得了质心的移动轨迹。速度可由两时刻弹丸在空间中运动的距离除以时间获得,即
(7)
2.2.2 总攻角计算方法
在获得了弹丸质心、弹轴和速度矢量在图像平面上的投影后,就获得了总攻角在图像平面的投影。为每台高速摄影定义一个摄影屏幕面,该面与各自的图像平面平行且包含弹丸的质心,如图7所示。
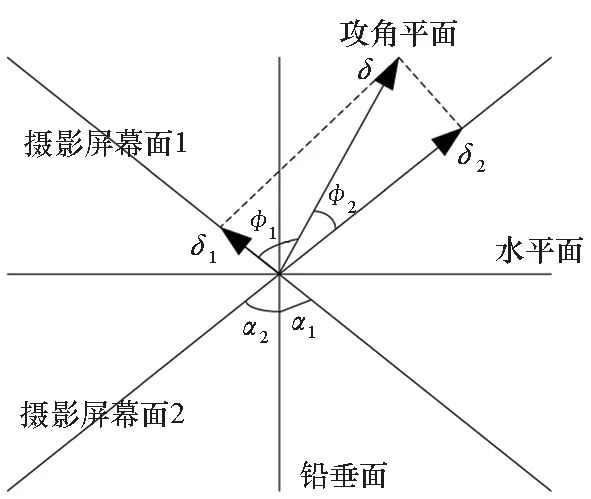
图7 摄影屏幕面示意Fig.7 Photography screen diagram
图7表示从炮位往射击方向看时各平面之间的位置关系。攻角平面是由弹轴和速度矢量组成的平面。为了便于描述角度在各平面之间的投影关系,这里引入一种角度的矢量表示方法。角度矢量方向表示该角度所在平面在空间中的位置,角度矢量的模长表示角度的大小。如图7所示,角度矢量δ的方向表示攻角平面在空间的位置,角度矢量δ的模长表示总攻角的大小。根据矢量投影关系有如下关系式
(8)
式中:φ1、φ2分别表示攻角平面与摄影屏幕面1、摄影屏幕面2之间的夹角,也是攻角平面的方位角;δ1、δ2分别表示总攻角在摄影屏幕面1、摄影屏幕面2上的投影分量。根据已知量δ1、δ2、α1和α2可得
(9)
φ2=α-φ1
(10)
(11)
至此,弹丸的总攻角和攻角平面的方位角都已获得。由式(11)可知,总攻角可由两个表达式求得。这里定义式(11)中的第一式为δ1的表达式,第二式为δ2的表达式。理论上,两个表达式是等效的,但实际测量时总会存在误差,此时两个表达式对总攻角的测量误差影响是不一样的。
3 总攻角误差分析
由式(8)~(11)可得,总攻角的表达式为
(12)
由式(12)可以看出,δ1、δ2和α为直接测量量,总攻角δ为间接测量量,且只与这三个量有关。根据式(12)可得出总攻角函数的系统误差和随机误差。根据误差传递理论[15]可知,总攻角函数的系统误差为
(13)
式中,Δδ1、Δδ2和Δα分别表示三个直接测量量的系统误差,∂δ/∂δ1、∂δ/∂δ2和∂δ/∂α分别表示三个直接测量量的误差传递系数。
随机误差是用表征其取值分散程度的标准差来评定的,对于函数的随机误差,也是用函数的标准差来进行评定。假设δ1、δ2和α的随机误差是相互独立的,那么总攻角函数的随机误差为
(14)
式中,σδ1、σδ2和σα分别表示三个直接测量量的标准差。
分析式(13)~(14)可知,总攻角的误差和直接测量量的误差传递系数相关,所以必须控制这些系数的大小。直接测量量δ1、δ2的大小无法控制,而α的大小可以通过改变两台高速摄像机之间的位置关系进行控制,从而达到控制∂δ/∂δ1、∂δ/∂δ2和∂δ/∂α大小的目的。此外,由式(11)可知,总攻角可由两个式子求得,可以通过选择不同的表达式控制三个直接测量量的误差传递系数。由式(12)可知,求解总攻角的两个表达式虽然不同,但在形式上完全相同,因此可以只研究其中一个表达式,探究表达式对误差的影响。选式(12)中的第一个表达式,可得
(15)
(16)
(17)
其中
(18)
式(17)比较复杂,求使得∂δ/∂α取最小值的α比较困难。可以通过编程,直接求得不同范围所对应的∂δ/∂α值,然后通过比较选择合适的α即可。
当δ2/δ1=1时,α值与∂δ/∂α之间的关系如图8所示。

图8 ∂δ/∂α与α的对应关系Fig.8 Relationship between ∂δ/∂α and α
从图8中可以看出,当δ2/δ1=1时(即不存在进动运动),α取越小越好,这表明高速摄像机的光轴垂直于攻角平面时由α引起的误差最小。当α接近180°时,∂δ/∂α趋于无穷大,这表明高速摄像机的光轴越接近平行于攻角平面时,由α引起的测量误差越大。
α的理论取值范围为0°~180°。若α取太小,此时有效视场大,存在总攻角平面与两个光轴都接近平行的情况;若α取太大,此时有效视场小,也存在总攻角平面与两个光轴都接近平行的情况。总结以上分析可知,实际测量时将α设置为90°是最利于减小测量误差的,因为总攻角平面与一台高速摄像机的光轴平行时,与另一个光轴肯定是垂直的。
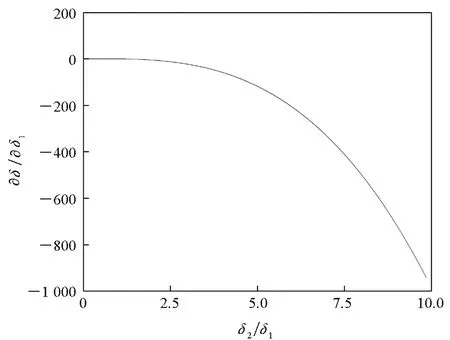
弹丸实际运动时肯定是有进动存在的,攻角平面也时刻在变化,所以无法保证高速摄像机的光轴垂直于攻角平面。不仅如此,由于弹丸的进动是一个圆运动,进动角的取值可以是0°~360°。在测量的时间段内,弹丸的攻角平面完全有可能和其中一台高速摄像机的光轴平行。所以在实际测量过程中,无法保证δ2/δ1=1,该比值可能取很大,也可能取很小。图9给出了∂δ/∂δ1和∂δ/∂δ2随δ2/δ1的变化关系。
(a) ∂δ/∂δ1与δ2/δ1的对应关系(a) Relationship between ∂δ/∂δ1 and δ2/δ1
由图9可知,当δ2/δ1很大时,∂δ/∂δ1和∂δ/∂δ2的值也很大,这对误差的抑制是不利的。此时,对于总攻角的δ2表达式,δ1/δ2很小,对应的∂δ/∂δ1和∂δ/∂δ2值也很小。所以在选取总攻角表达式时,应选取δ1和δ2中较大的那个量所对应的表达式。这样就可保证δ1和δ2的比值始终小于1,从而使三个直接测量量的误差传递系数都较小。
4 靶场实验验证
为验证该测量方法,进行了靶场实验。实验的射角是51°,初速大约为930 m/s。为了不受炮口烟雾影响且尽可能多地捕捉弹丸的飞行并拍摄到清晰的图像,Lx设为75 m,L1和L2均设为92 m。由前文的分析和几何关系可知,当前实验条件下两台高速摄像机的仰角均设置为45°。靶场布置以及参数设置分别如图10所示。

图10 靶场实验布置示意Fig.10 Diagram of shooting range experiment layout
实验获取了发射瞬间炮口左右两侧的高速摄像机视频。将视频逐帧转化成图像,并对图像进行弹丸轮廓提取和弹轴绘制。为了便于显示处理过程,选取了5张图像中的弹丸绘制在同一张图像中,并绘制了弹丸的轴线和质心连线。图11显示了射击平面左右两侧视频处理的结果。

(a) 左侧(a) Left side
图12表示POSIT算法和本文算法处理的弹丸速度测量结果。由POSIT算法外推得到的弹丸初速为925.4 m/s,本文方法外推获得的弹丸初速为930.2 m/s,初速雷达测得的弹丸初速为930.8 m/s。线性外推会将测量误差放大,以初速雷达测量值为参考,本文算法外推得到的初速结果误差为0.6 m/s,那么在弹道中速度的测量误差不会大于该值。

图12 速度测量结果Fig.12 Velocity measurement results
图13表示POSIT算法和本文算法处理的弹丸质心位置测量结果。由图13可知,POSIT算法外推得到的炮位在地面坐标系中的坐标为(12,7,0.6) m,本文方法外推得到的炮位相应坐标为(0.3,0.1,0.02) m。根据前文对测量系统的介绍可知,理论的炮位坐标应该为地面坐标系的原点。本文外推得到的炮位坐标应该是测量误差最大的点,所以该测量方法对弹丸质心位置的测量误差不超过0.3 m。

图13 位置测量结果Fig.13 Position measurement results
结合图12和图13可知,本文所提出的双高速摄像机交汇算法在弹丸炮口信息处理方面要优于POSIT算法。
图14表示POSIT算法和本文算法处理的弹丸总攻角测量结果。从图14可以看出,本文算法很好地测出了总攻角的摆动过程,但测量时间较短,不足一个周期。相较于POSIT算法,本文算法优势明显,POSIT算法几乎没能捕捉到弹丸的摆动过程。

图14 总攻角测量结果Fig.14 Measurement results of total angle of attack
对于图14的第一个时刻点,δ2/δ1为9.8,此时选择δ1表达式计算总攻角的结果为0.31°,而选择δ2表达式计算总攻角的结果为3.2°,二者相差一个数量级。结合整段攻角变化曲线和POSIT算法的结果可知,3.2°应该更为准确。因此可以认为前文的误差分析结论是正确的,即选取总攻角表达式时,应选取δ1和δ2中较大的那个量所对应的表达式。
5 结论
本文提出了一种双高速摄像机交汇测量弹丸炮口信息的方法,推导了炮口信息数据处理的公式,并在靶场实验中对该方法进行验证,得出以下主要结论:
1)实验表明,本文所提出的测量方法速度测量误差不超过0.6 m/s,弹丸质心位置测量误差不超过0.3 m。
2)通过对总攻角函数的误差建模与分析可知, 取90°时,整体误差较小,选取总攻角函数表达式时,应取δ1和δ2中较大的那个量所对应的表达式。
3)本文所提位置、姿态数据处理算法要优于POSIT算法,测量精度更高。
4)本文所提的测量方法简单易行,便于靶场实施,不受射击条件限制,可用于靶场实验、验收等工作中。

