多窗口谱图分析的低截获概率雷达信号识别*
刘鲁涛,陈林军,李 品
(1. 哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001; 2. 南京电子技术研究所, 江苏 南京 210000)
自从雷达技术问世以来,由于其重要的检测应用,该技术取得了非凡的成就[1]。同时,雷达对抗技术也在逐渐发展,对抗系统能够在雷达发现目标之前截获信号并进行干扰。而低截获概率(Low Probability of Intercept, LPI)雷达具有良好的隐身效果,这对侦收到的雷达辐射源信号识别提出了巨大的挑战[2-3]。因此,在现代雷达电子对抗系统中,LPI雷达信号识别已成为研究热点之一[4]。现有的文献中,有一些LPI雷达信号识别技术首先对雷达信号进行特征提取,然后将提取的特征送入分类器中进行分类识别。
对于特征提取,一般采用时频分析将一维的雷达信号转换到时频域,得到时频图像,常见的时频分析算法有短时傅里叶变换(Short-Time Fourier Transform, STFT)、维格纳分布(Wigner-Ville Distribution, WVD)[5-6],平滑伪维格纳分布(Smoothing Pseudo-Wigner-Ville Distribution, SPWVD)[7]和崔威廉姆斯分布(Choi-William Distribution, CWD)[2-3]。另一方面,对于分类识别部分,由于卷积神经网络(Convolutional Neural Networks, CNN)在图像识别领域[8]内极高的识别准确率,不少学者将CNN与LPI雷达信号识别相结合:文献[9]将信号的脉宽、载频和脉冲重复间隔作为特征空间,形成三维图像,输入到CNN中实现58个独立辐射源的识别;文献[10]利用CWD时频变换和进化神经网络(Evolutionary Neural Networks, ENN)进行辐射源信号的识别,在信噪比-2 dB条件下,对8种辐射源信号的识别率达到94.7%;文献[11]将时频图像和图像形态学操作相结合,利用图像形态学操作消除时频图像中的部分噪声,并将时频图像送入CNN,实现了8种辐射源信号的识别。
针对低信噪比条件下多种类辐射源信号识别率低的问题,本文提出基于多窗口谱图(Multi Window SPectrogram, MWSP)分析与迁移学习ImageNet-VGG-f网络相结合的LPI雷达信号识别算法,即MWSP-ImageNet-VGG-f。多窗口谱图算法采用Hermite函数作为窗口函数进行谱图分析,通过不断改变Hermite多项式得到一系列窗函数,利用它们进行谱图分析,使得有效信号得到了好的聚集而分散了噪声的干扰聚集。该方法首先利用多窗口谱图变换对辐射源信号进行时频变换,转换为时频域的时频图像,再将时频图像送入VGG-f网络中进行分类识别。
1 LPI雷达信号模型与识别流程
侦察接收机的截获作用范围小于雷达对目标的探测范围,这说明此时雷达能够探测目标但是侦察接收机无法作用于雷达,这种雷达辐射的信号称为“低截获概率雷达信号”。脉冲压缩技术能够使雷达信号满足低截获概率特性,常见的脉冲压缩方法有频率调制、相位调制等。
LPI雷达信号调制类型识别流程一般由时频变换和分类识别组成,首先将时域信号进行时频分析以得到时频域的图像,再将时频图像进行一系列预处理,最后送入分类网络中进行识别。
1.1 信号模型
雷达接收机侦收到的信号由信号和噪声构成,它的数学模型为:
s(t)=x(t)+n(t)
(1)
(2)
其中:s(t)表示接收的雷达信号;x(t)表示调制信号;n(t)表示高斯白噪声;A表示幅度,因为雷达信号一般不采用幅度调制,A是常数;T,fc和φ0分别是脉冲宽度、载频和初始相位;φ(t)是相位调制函数。
(3)
后续仿真中出现的含噪信号是通过先计算信号的功率,然后根据信噪比来计算噪声功率以得到噪声后再与原始信号相加而得。
常见的LPI雷达信号调制方式包括频率调制和相位调制,例如,线性调频信号是一种频率调制信号,频率随时间线性变化,其信号表达式为:
(4)
非线性调频信号也是一种频率调制信号,频率随时间非线性变化,常见的非线性调频信号有正弦调频信号、三次调频信号和任意频率调频信号等。下面主要介绍正弦调频信号(Sinusoidal Frequency Modulation, SFM),其信号表达式为:
(5)
上述信号和其他LPI雷达信号的参数设置在后续调制方式识别仿真研究过程中给出。
1.2 调制信号特征提取与识别流程
LPI雷达信号调制识别过程主要分为两个过程,首先通过时频分析算法产生时频图像;然后对时频分布图像进行预处理,如:二值化、调整图像大小等,调整图像使其满足分类网络的输入条件;最后将预处理过的时频图像送入分类网络进行调制方式识别。具体分类识别流程如图1所示。
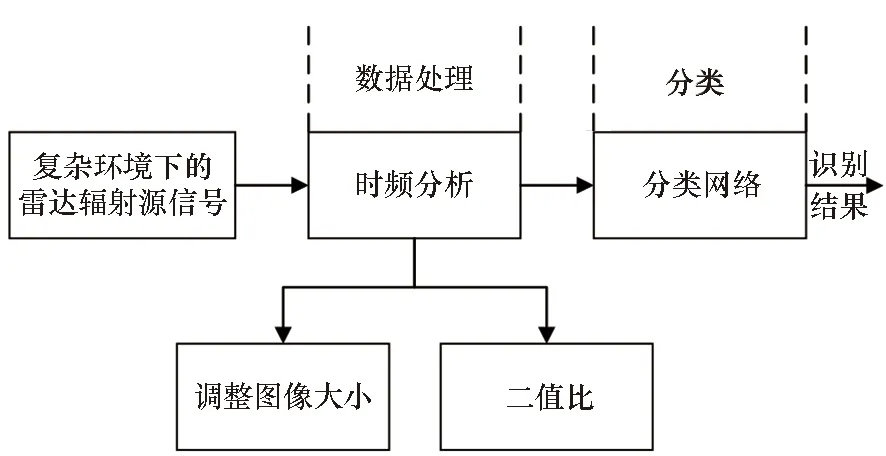
图1 LPI雷达信号调制识别流程Fig.1 LPI radar signal modulation recognition process
2 MWSP时频分析算法
时频分析是处理诸如雷达信号等非平稳信号的有效工具,时频图像的形状有助于显示不同类型的雷达信号之间的差异。常用的时频分析方法有STFT、WVD、CWD变换等。WVD定义为:
(6)
WVD虽然具有良好的时频分辨率,但是由于交叉项的存在,WVD对噪声非常敏感。
STFT是最常用的一种时频分析方法,该方法通过时间窗口内的截取信号来表示某一时刻的信号特征,定义为:
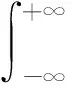
(7)
而谱图[12]是由STFT得到的,其定义式为:
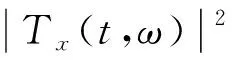
(8)
多窗口时频谱图算法是多窗口理论结合谱图的时频分析方法,多窗口思想首次由Thomson提出,利用多个正交窗口求各自的谱估计[13],再综合在一起,用来增加谱估计的精度和减少谱估计的振荡,而Bayram等应用Hermite函数将Thomson提出的多窗口方法扩展到时间-频率平面[14]。
(9)
将多窗口和谱图分析结合,采用Hermite函数作为窗口函数进行时频谱图分析,在低信噪比条件下,达到良好的抗噪性能。Hermite函数具有正交性,在时间-频率平面具有良好的时频聚集性,图2是Hermite函数时域图(图中坐标无实际单位,仅表示关系)。
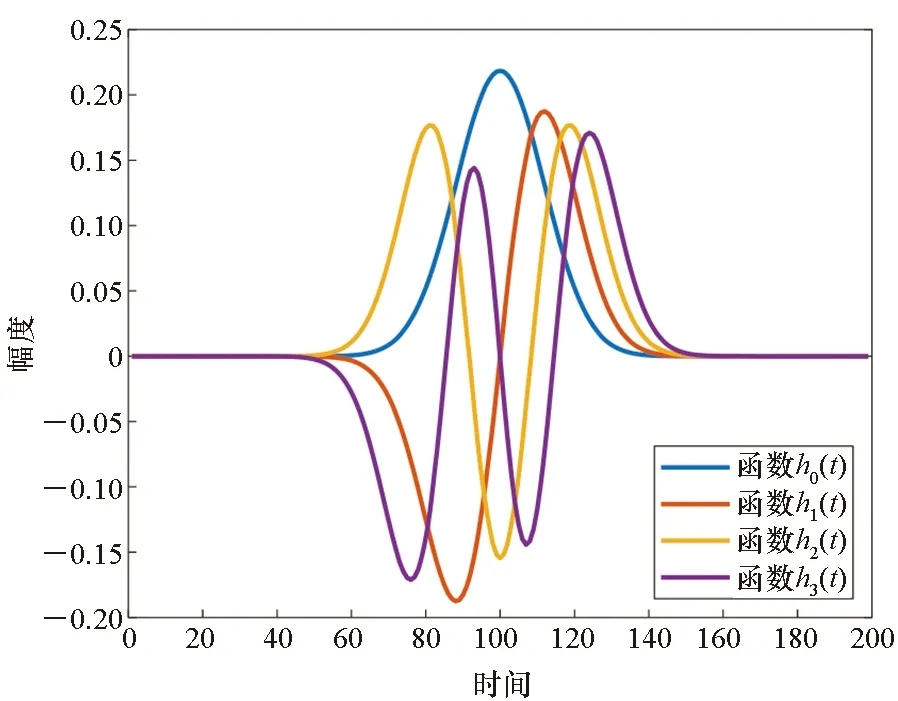
图2 Hermite函数时域图(k=0,1,2,3)Fig.2 Hermite function time domain diagram(k=0,1,2,3)
k次Hermite函数[15]定义为:
(10)
式中,Hk(t)(k∈N)是k次Hermite多项式。
(11)
容易看出:H0(t)=1,H1(t)=2t,H2(t)=4t2-2,H3(t)=8t2-12t,…。
多窗口谱图算法定义如下:
(12)
式中,dk是加权系数,且∑dk=1。
采用MWSP和CWD算法分别对典型的LFM信号进行信噪比对比仿真实验,信噪比范围设定为[-8,-2] dB,步进为2 dB,对比MWSP算法、CWD算法进行全局阈值二值化后的时频分布图像。仿真结果如图3所示。
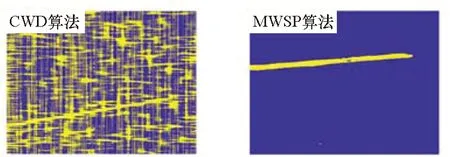
(a) SNR=-8 dB
仿真结果表明:MWSP算法对比CWD算法具有良好的抗噪性能,在信噪比低于-6 dB时,CWD算法产生的时频分布图像已经完全被噪声淹没,无法正常分辨;而MWSP算法产生的时频分布图像具有良好的抗噪性能。
3 ImageNet-VGG-f网络
深度卷积神经网络模型具有良好的分类效果,但需要经过上百万个参数的训练,所以Deep-CNN在训练的时候需要大量的有标签样本和时间才能够得到具有良好泛化能力的模型。在训练样本不足、训练时间有限的条件下,可以利用预训练好的模型来迁移到新的数据中,将训练数据送入预训练的网络中进行训练,在短时间内达到良好的分类识别的效果。
预训练ImageNet-VGG-f网络通过ImageNet数据集完成训练[16],ImageNet任务包含1 000类图像的分类与定位。VGG网络模型采用3×3的卷积核,2×2的池化核,用2个3×3的卷积核堆叠等同5×5的感受野,用3个3×3的卷积核堆叠等同7×7的感受野。虽然采用的是小卷积核,在相同步长情况下,产生的特征图跟大卷积核相差不大,但是计算量小了很多。VGG网络结构虽深但比较简单,因为只有CNN足够深,才能够更好地表达图像特征。
采用ImageNet-VGG-f网络模型进行调制类型识别[17],对于该网络结构的研究可以对Deep-CNN网络迁移到调制识别的有效性进行深入了解,为进一步识别分类奠定理论基础。ImageNet-VGG-f网络结构如表1所示。
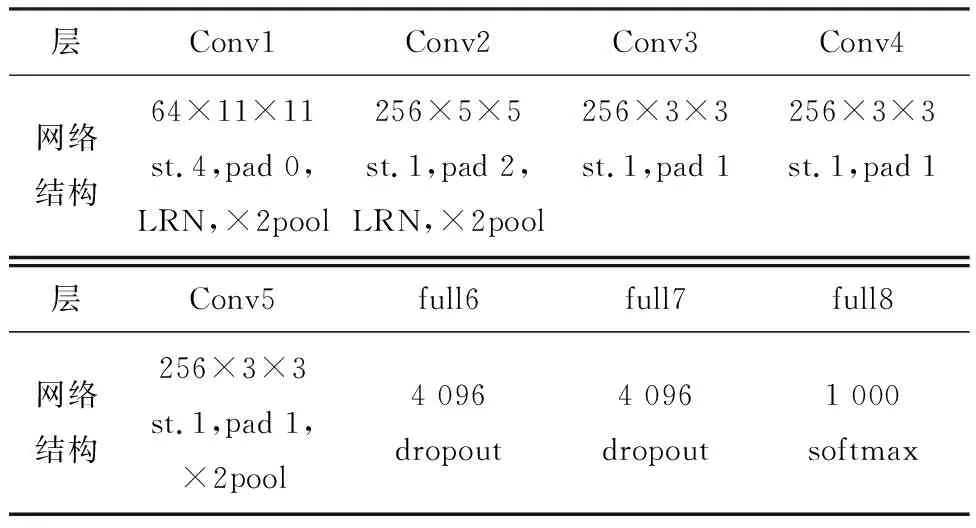
表1 ImageNet-VGG-f网络结构
ImageNet-VGG-f网络调制识别步骤如下。
步骤1:根据仿真参数产生LPI雷达信号集;
步骤2:利用MWSP、CWD、SPWVD算法对雷达信号进行时频变换,产生时频图像,并对时频图像进行预处理,产生224×224×3大小的RGB图像集;
步骤3:构建迁移网络模型,保持预训练的ImageNet-VGG-f网络参数和网络结构不变,组成VGG-f迁移网络模型;
步骤4:将步骤2的图像集送入VGG-f迁移网络模型,经过特征提取后,full8层得到的特征图大小为1×1 000;
步骤5:利用softmax对时频图像的数据集进行分类,并验证SPWVD、CWD和MWSP算法产生的时频图像的识别率。
4 实验结果与分析
4.1 MWSP算法仿真分析
采用MWSP算法对常见的LPI雷达信号进行时频分析,观察各个信号的时频图像。
实验1通过AWGN信道,信噪比SNR=0 dB,MWSP算法对LFM、QFM、Costas、SFM、EQFM、T1这6种常见的LPI雷达信号进行时频变换,如图4所示。可以看出,在低信噪比0 dB条件下,采用MWSP算法产生的六种时频图像依旧有良好的可分辨性。

(a) LFM (b) QFM
4.2 调制识别仿真分析
采用MATLAB仿真环境产生7种常见的LPI雷达信号进行调制识别仿真实验,进一步验证MWSP算法对识别性能的影响。这7种LPI雷达信号分别为LFM、QFM、Costas、EQFM、SFM、T1和ANYFM。
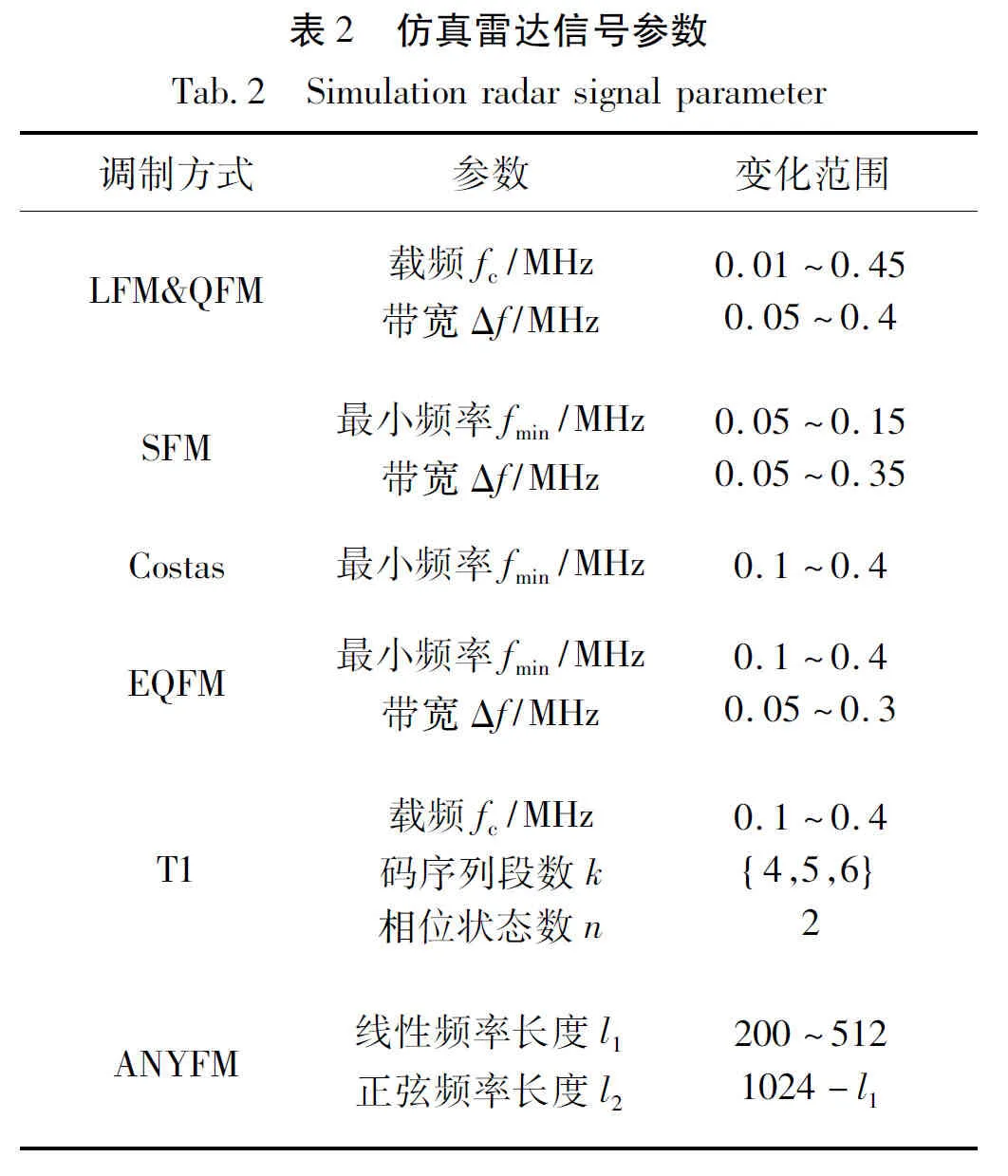
仿真参数设置:为了在时频分析中使用快速傅里叶变换(Fast Fourier Transform, FFT),将信号时域采样点数目统一为1 024。在实际情况中,存在不同载频的信号,接收机接收到的信号也是不同载频的,对信号参数设置载频范围,调整时频图像的位置,具体的参数设置如表2所示。每种信号随机产生500个作为训练数据,共3 500个训练信号,加入不同信噪比的高斯白噪声,分别利用MWSP算法、CWD算法和SPWVD算法产生每种信号100个作为测试信号。
根据表2的仿真参数,对测试信号进行随机添加噪声,信噪比范围从-8 dB到8 dB,利用SPWVD、CWD和MWSP算法产生时频图像,经过时频变换后产生的是1 024×1 024大小的时频矩阵,然后经过全局阈值二值化处理得到二值图像。在测试部分,一共设置9个测试集,他们的信噪比分别是-8 dB、-6 dB、-4 dB、-2 dB、0 dB、2 dB、4 dB、6 dB和8 dB,每个测试集包含700个测试样本,随机产生不同参数的信号,参数范围如表2所示。
ImageNet-VGG-f预训练网络模型输入要求为224×224×3的RGB图像,在送入网络训练和测试之前,采用图像处理中的双三次插值算法将时频图像的维度压缩至224×224,并且通过拼接将二值图像拼接成三维图像,满足网络输入要求。
实验2高斯白噪声环境下,信噪比为0 dB,对MWSP算法产生的测试集进行仿真实验,观察每种信号的识别率。
当SNR=0 dB时,对于本文生成的7种LPI雷达信号都能够正确识别,平均识别正确率达到99%,T1信号识别正确率为94%,且LFM、QFM、Costas、ANYFM、SFM、EQFM信号识别正确率均为100%。可以得到结论,MWSP算法产生的时频图像具有良好的抗噪性能,在低信噪比条件下依旧有很好的表现,为低信噪比情况下的LPI雷达信号调制识别研究提供了新思路。
实验3对三种算法产生的9种测试集进行对比实验,信噪比从-8 dB到8 dB,步进为2 dB,实验过程中,分别对三种算法产生的时频图像进行训练和测试。
三种算法在不同信噪比条件下的平均识别正确率如图5所示,从图中可以看出,在SNR<0 dB时,MWSP算法明显优于另外两种算法,CWD和SPWVD时频分析方法受噪声干扰严重,无法对LPI雷达信号进行有效的分析,识别正确率低;随着信噪比逐渐增加,大于0 dB之后三种算法的识别正确率趋于平滑,基本保持很高的正确率。仿真结果证明了MWSP算法良好的抗噪性能,为低信噪比环境下的LPI雷达信号调制识别提供了可行性。
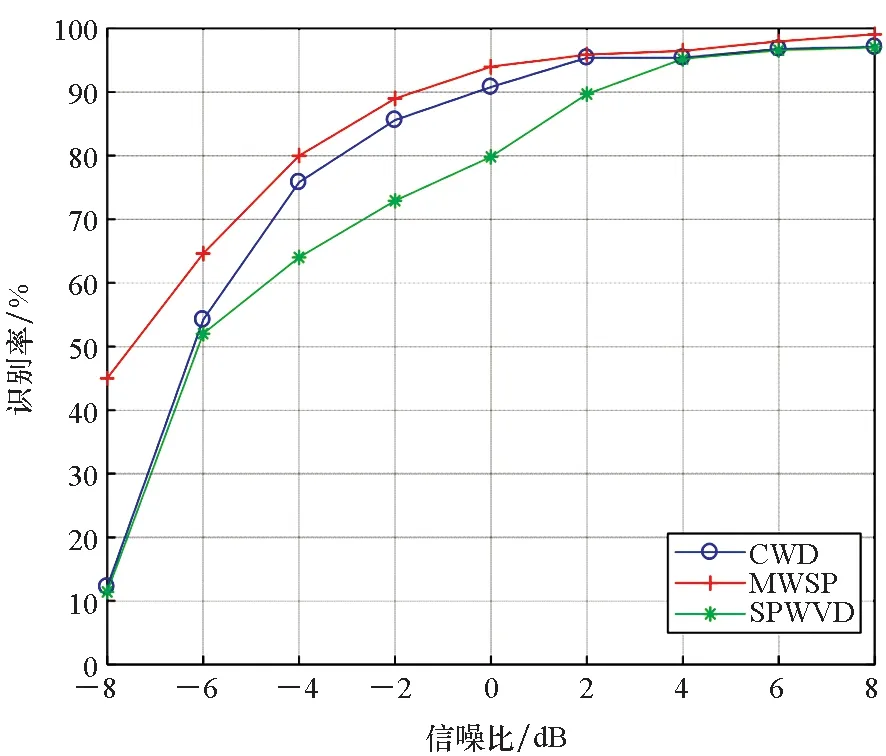
图5 三种算法识别准确率对比Fig.5 Comparison of recognition accuracy of three algorithms
5 结论
本文针对LPI雷达信号常规时频分析方法产生的时频图像受噪声干扰严重的问题,使用MWSP算法产生时频分布图像,有效地降低噪声干扰,在低信噪比条件下,使不同LPI雷达信号的时频图像具有良好的可辨识性。产生时频图像之后,经过全局阈值二值化、双三次插值压缩和拼接,利用ImageNet-VGG-f迁移神经网络完成了LPI雷达信号分类识别。仿真条件相同时,将MWSP算法与传统的CWD和SPWVD算法进行对比实验,将三种时频分析方法产生的图像分别送入ImageNet-VGG-f迁移神经网络中进行识别,实验结果表明MWSP算法具有更佳的抗噪性能,产生的时频图像噪声干扰少,在低信噪比情况下,MWSP算法的LPI雷达信号识别正确率明显高于另外两种算法。

