微型桥梁索力测量毫米波雷达*
王 建,王 翔,周智敏
(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 中铁大桥科学研究院有限公司, 湖北 武汉 430034)
中国在国家基础建设上的大力持续投入,各类桥梁在2018年已超100万座[1],每年开工建筑的桥梁约为1万余座,中国正由世界“桥梁大国”向“桥梁强国”迈进。斜拉桥、悬索桥应是大跨度桥梁的首选结构形式,拉索是这类大型桥梁的关键承力构件,直接影响桥梁结构的内力分布和桥面线形,索力的绝对量、动态改变量和索力的分布是评价桥梁健康状态的核心指标,因此拉索索力的快速高精度测量具有十分重要的意义[2]。目前索力测试的方法较多,其中包括压力表测定法、压力传感器测定法、电磁测量法等,这些技术均存在各种不足,或者仅在特定场合适用,因此没有广泛采用。目前在实际工程应用中频率法使用广泛,具有快速、方便、实用、可重复测试的特点,可靠性较好,且精度在允许的范围内[3]。频率法索力测量的常规传感器是加速度计,它存在的不足:传感器难以固定至拉索跨中,测量数据受到端部拉索减振器的干扰;经常出现无法直接测到基频的情况,需采用高阶频率推算基频,进而造成一定的测量误差。
干涉形变雷达是一种新型位移测量传感器,相对于常规加速度计、高清视频等传感器,具有精确、非接触、实时连续、作用距离远、多点同时探测、环境适应性强等优点[4]。本文设计实现了一种K波段24 GHz形变测量雷达,具有优良的探测性能,但存在结构复杂、成本高、集成度低等问题[5]。提高干涉雷达形变测量精度对雷达体制、高稳定信号源、系统误差补偿、雷达信号处理、大气干扰抑制等均提出较高的要求[5]。
毫米波(MilliMeter Wave, MMW)雷达工作于30~300 GHz,具有分辨率高、体积小、功耗低等优势,但商用MMW雷达普遍存在相噪大、作用距离近等问题。本文针对这些问题,研制了一个MMW雷达试验系统,建立了一套控制MMW雷达性能的参数集,并与某实用K波段索力测量雷达进行性能对比分析,验证了新雷达的有效性。
1 形变雷达索力测量原理分析
1.1 频率法索力测量原理
假设拉索静力平衡位置微幅振动方程为[6]:
(1)
式中,EI为抗弯刚度,v=v(x,t)为拉索振动产生的竖向位移,y=y(x)为拉索自重产生的竖向位移,T为水平拉索索力,h为由于振动所产生的水平附加索力,k′为单位长度的弹性参数,c′为单位长度的阻尼参数,m为单位长度的质量,t为振动对应的时间,x为拉索横向坐标值。
实际施工测量过程中,一般假设拉索为张紧的弦,不考虑其抗弯刚度、垂度和阻尼,并忽略其他边界条件,可得到简化索力估计为[4]:
(2)
其中:l是拉索长度;fn为拉索的n阶自振频率,一般具有f1=fn/n的关系。
1.2 拉索的雷达散射特性分析
桥梁拉索为多芯钢缆编绕结构,在裸露状态下拉索的周期结构容易引起Bragg散射,为了增加钢缆的使用寿命,拉索外部通常会套上一层保护套。此时钢缆可建模为圆柱体,圆柱体后向散射(Radar Cross Section, RCS)的公式为[7]:
(3)
其中,H表示圆柱体长度D为圆柱体的直径。仿真结果表明,桥梁拉索仅在θ=0°入射角(法向)存在散射峰,其他位置RCS逐渐衰减[8]。
拉索的目标散射特性要求使用雷达进行索力测量时,雷达到拉索的垂线方向应当在雷达波束范围内。
1.3 形变雷达位移测量原理
线性调频信号(Linear Frequency Modulation, LFM)是近程高分辨雷达最常用的信号体制,其频率随时间连续线性变化,假设发射LFM信号为:
(4)
其中:f0为信号的起始频率;Tp为扫频周期(Pulse Repetition Interval, PRI);k为调频斜率;t为一个调制周期内的时间,忽略信号幅度A的影响。对于距离为R的目标,其接收信号为:
Sr(t)=St(t-τ)
(5)
其中,τ=2R/c表示目标双程传输时延。形变测量雷达带宽大,一般采用去调频接收体制以降低数模转换(Analog to Digital, AD)采集单元的成本。将回波信号与发射信号混频,并经过低通滤波后的中频信号为:
SIF(t)=exp(j2πf0τ)exp(j2πkτt)exp(-jπkτ2)
(6)
式中,第一项为目标引起的相位延迟,第二项为线性相位,决定了目标所在距离,第三项是去调频引起的二次相位误差。对中频信号进行傅里叶变换即可实现脉冲压缩[5]:
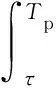
=exp(-jπkτ2)exp[j2π(f0+f)τ]·
sinc[π(kτ+f)(Tp-τ)]
(7)
可见脉冲压缩后,距离为R的目标其峰值出现在f=-kτ处,其分辨率(频率分辨率)由时长Tp-τ决定。形变测量雷达利用宽带信号对空中的拉索进行照射,获取高分辨率一维距离图像,然后根据脉冲压缩波峰f=-kτ确认拉索位置,以一定的重复频率(Pulse Repetition Frequency, PRF)记录波峰位置处的相位φ(ts)=2πf0τ(ts)+πkτ(ts)2≈2πf0τ(ts),因此可得目标位移量与相位导数的关系为:
(8)
由于桥梁形变缓慢并且幅度较小,因此当雷达的PRF较大,可用数字差分替代导数,可得:
(9)
因此,雷达通过时间差分干涉相位可以推算拉索位置的微小变化。由于相位测量仅能获得相位主值,应当设计PRF以保证无相位模糊[5]。
随后对ΔR积分可得到振动形变量d,最后对d做傅里叶变换可得到拉索的振动频谱,更高的形变精度对准确提取振动基频更加有利,工程经验表明形变精度优于0.1 mm即可基本满足应用要求[2]。
2 MMW 77 GHz雷达系统参数设计
本文研究的77 GHz MMW雷达面向未来无人驾驶和智能交通等应用领域,国内外77 GHz毫米波雷达芯片产品较多,其中以美国TI公司的AWR系列芯片为代表。AWR芯片采用互补金属氧化物半导体(Complementary Metal Oxide Semiconductor, CMOS)工艺,将雷达系统中的信号源、混频器、倍频器、低噪声放大器(Low Noise Amplifier, LNA)、滤波器、AD采集、存储器、信号处理和控制单元等集成在一个芯片内,可显著降低雷达系统成本[9]。雷达芯片的高集成带来的问题包括:发射功率低、系统隔离度降低、相位噪声增大、信号处理能力受限等。
干涉形变测量雷达形变测量精度与外部环境、系统稳定度和目标回波强度相关,其中外部大气和振动环境误差在后端抑制;单芯片MMW雷达系统稳定度可通过温补高稳晶振设计保证;回波强度决定了目标信噪比(Signal Noise Ratio, SNR),而SNR与干涉测量相位误差成反比[10],可得形变精度为:
(10)
根据MMW雷达特性分析,制约作用距离的两个主要因素为中频带宽和功率孔径积。
根据式(6)中的关系,最大作用距离Rmax1与最大中频频率fIFmax的关系为Rmax1=cfIFmax/2k。为了防止信号混叠,AD复数采样频率fAD≥fIFmax,因此可得:
(11)
此外,根据雷达方程,在发射功率Pt、发射天线增益Gt、接收天线增益Gr、系统损耗Ls、最小可检测信号功率Smin已知的情况下,最大作用距离可表示为:
(12)
从式(10)可知,改善形变精度与提高SNR和发射功率是一致的。利用集成MMW芯片设计雷达系统,最大作用距离的设计余地较小,其中可变参数为k、Gt、Gr,根据它们得到Rmax1和Rmax2的最小值,即为雷达系统的最大作用距离。
此外,考虑到防止相位模糊的因素,MMW索力测量雷达的参数约束集为PRF、k、Gt、Gr。
3 MMW雷达与K波段雷达性能对比分析
基于TI公司AWR1642设计MMW雷达,重点优化了发射和接收天线增益,由参考设计10 dBi[9]提高到18 dBi以上,雷达的工作参数如表1所示。AWR1642具有2个发射和4个接收通道,收发天线线性排列,接收天线间距为λ/2,发射天线间距为2λ,可形成8个间距为λ/4的等效收发共用天线。为了提高形变测量精度,从提高通道隔离度的角度,选择间隔最大的T2和R1天线组合工作。该MMW雷达(见图1)通过转接板固定于三脚架之上,尺寸约88 mm×58 mm×15 mm,质量约39 g。
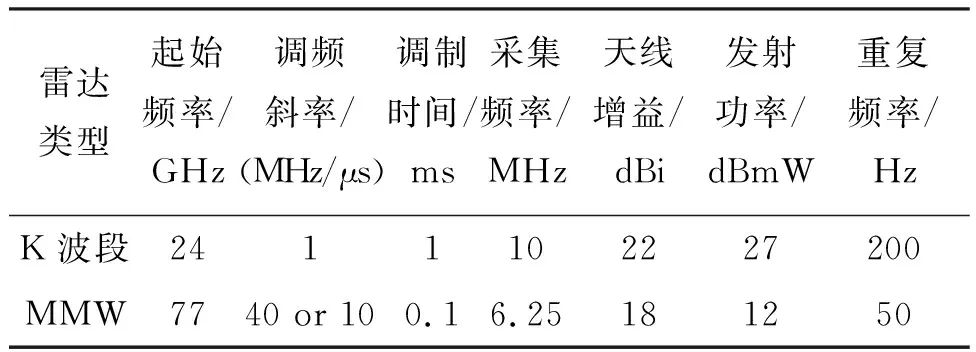
表1 两个雷达的工作参数
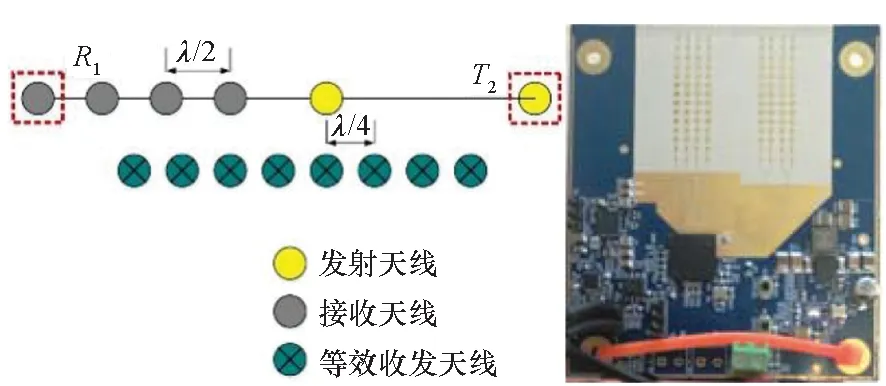
图1 MMW雷达阵列模型与照片Fig.1 Antenna array model and a picture of the MMW radar
3.1 形变测量精度对比分析
测试目标为0.2 m三面角,距离雷达约2.5 m,MMW雷达的调频斜率40 MHz/μs,有效信号带宽约为3.3 GHz,K波段雷达有效信号带宽约1 GHz。两种雷达的脉冲压缩结果如图2所示,由于MMW雷达信号带宽更大,距离分辨率为K波段雷达的3倍,距离分辨率更优,因此对区分邻近拉索时更具优势。三面角在MMW雷达图像的位置为2.58 m,SNR约为35 dB,在K波段雷达中位置为2.56 m,SNR约为51 dB。
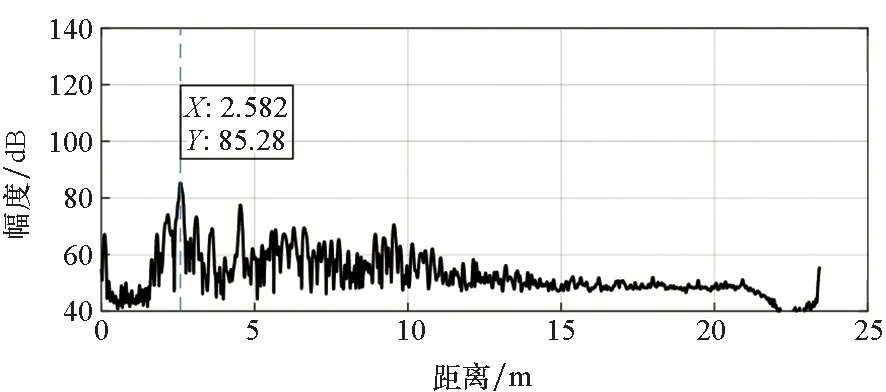
(a) 三面角的MMW雷达一维距离像 (a) One dimensional MMW radar image of a trihedral
时间差分干涉得到三面角的形变曲线如图3所示,其中MMW雷达的形变测量方差(STandard Deviation, STD)可为0.001 45 mm,K波段雷达下的方差为0.000 61 mm,两者相差7.5 dB。由于两种雷达波长相差10.1 dB,SNR相差16 dB,根据式(10)计算的形变精度相差约5.9 dB,实测和理论值基本相符。
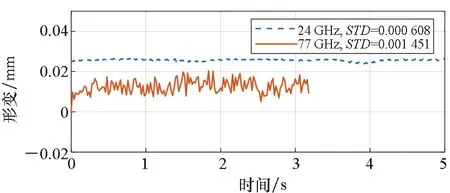
图3 三面角形变曲线和形变方差Fig.3 Displacement curves and STDs of the trihedral
3.2 实际拉索探测试验对比分析
根据式(11),可以计算得到,当调频斜率k=40 MHz/μs时,最大不模糊作用距离为Rmax1=23.44 m,作用距离偏小,难以满足野外实际桥梁拉索测试要求,因此将k降低至10 MHz/μs,最大距离增加到93.75 m。测试桥梁为长沙市二环跨浏阳河的洪山桥,该桥是跨径超过200 m的特大型斜拉桥,桥中心东西两面各有13根拉索,试验照片如图4所示,两种雷达获得一维距离像如图5所示,可见拉索的SNR在MMW雷达中多为10~20 dB,而在K波段雷达中多为20~40 dB,两种雷达在相同距离上拉索的信噪比差异与三面角试验相近。
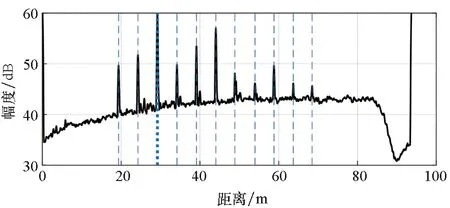
(a) 拉索的MMW雷达图像(a) MMW radar image of a group of cables
取第5根拉索进行分析,可得其形变曲线和振动频谱如图6所示。两次试验时刻不同,桥上交通不同,因此形变曲线存在差异,然而通过频谱分析可知,两种雷达均能够准确获取拉索的基频。需要注意的是:MMW雷达波长更短,更容易产生相位模糊,当相邻时刻形变量超过λ/4时就会出现形变跳变,如图6(a)所示:形变曲线在6.4 s时刻出现了由相位模糊造成的跳变。
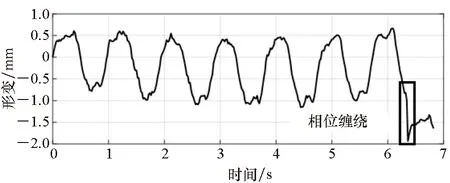
(a) MMW雷达测量的形变曲线(a) Displacement curve measured by the MMW radar
对所有拉索均按照类似方法计算基频后,得到的基频曲线如图7所示,可知MMW雷达的测量结果与K波段一致性良好。虽然MMW形变数据精度比K波段雷达稍差,但基频计算中的傅里叶变换对测量噪声具有一定的容忍度,因此可推测MMW能够测量更远距离或更低散射拉索的索力,能够满足实际工程测量应用需求。
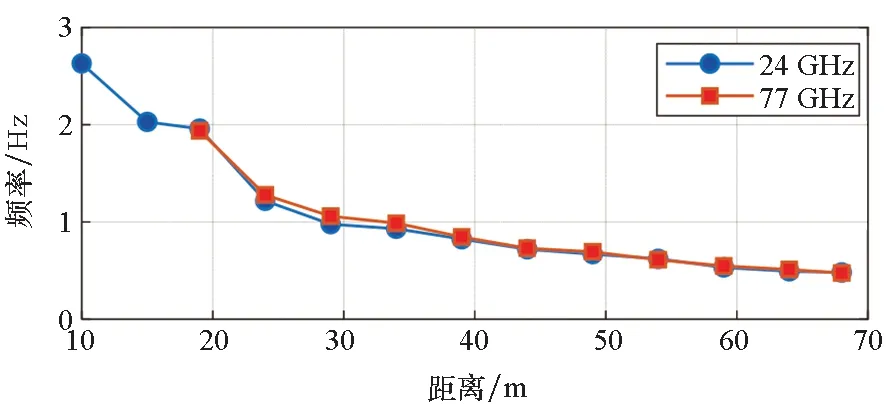
图7 西面11根拉索的基频对比Fig.7 Comparison of base frequencies of the 11 west cables
4 结论
本文从频率法索力测量、拉索雷达散射响应、差分干涉拉索形变测量等方面详细描述了形变雷达索力测量的基本原理,设计了一种实用的MMW索力测量雷达,并与常规24 GHz索力测量雷达进行了性能对比,主要结论如下:
1)所设计的MMW雷达虽然体积功耗小,但是测量精度高,当SNR>35 dB时,形变精度优于0.01 mm;在参数集组合配置下,作用距离可达100 m以上,可满足大型桥梁拉索测量要求。
2)MMW雷达有效工作带宽更大,与K波段雷达相比,具有对近距离密集拉索测量的优势。
3)所研制的MMW雷达由于基于集成芯片设计,系统隔离度和发射功率受限,因此形变精度略低于24 GHz雷达,进而也限制了MMW雷达作用距离的进一步提升。
4)MMW雷达波长短,差分干涉测量容易造成相位模糊,需要以较高重复频率工作。
本文研究可为MMW雷达形变测量系统的设计、试验和性能优化提供参考,具有较大的工程实用价值。

