针对自适应滤波的组网雷达欺骗干扰优化策略*

王布宏，黄天奇，田继伟

(空军工程大学 信息与导航学院， 陕西 西安 710077)

空天非合作目标的多样性、复杂性与作战使用的灵活性，预警探测环境的综合性、快变性与难以预测性，情报保障需求的实时性、连续性与高精度性，给以单雷达探测为主体的预警探测系统提出了严峻的挑战，另外传统雷达所面临的“四大威胁”(电子干扰、隐身目标、反辐射摧毁和低空突防)也促使组网雷达成为现今雷达的发展热点[1-3]。组网雷达系统是对异地部署的，不同体制、功能、频段、精度和数据率的单一雷达进行实时远程控制和点迹集中融合处理，将指定区域雷达群的多部雷达装备以组网探测模式进行资源整合，形成一部具有高精度和高数据率的“可编程大雷达”，实现探测效能的综合集成[4-5]。它可以提高在复杂实战环境中对空中非合作目标的集群探测能力，增强雷达情报的准确性、连续性和时效性，因而组网区域整体抗电子干扰能力显著提升[6-7]。

因此，如何对组网雷达进行有效的欺骗干扰，成为当今研究的热点问题[8-10]。文献[11]按照视线法则推导了多架电子战飞机(Electronic Combat Air Vehicles，ECAV)编队飞行的一般运动学模型，提出了把ECAV从给定的任意初始状态转换到欺骗干扰队形的控制方法。文献[12]提出了按照比例导引法生成虚假航迹的方法，并建立了一个新的性能指标来评估虚假航迹的一致性。文献[13]在多站雷达中各雷达站相距不远的条件下，从空间分辨单元的物理含义入手，推导出了多站雷达在一定空间分辨率下，转发式干扰能对其进行有效干扰的条件。文献[14]研究了雷达位置侦测误差和ECAV预设位置误差对欺骗干扰的影响，提出了一种针对组网雷达航迹关联检测的偏差补偿机制。文献[15]针对现有研究的主瓣航迹欺骗干扰技术进行航迹规划时只考虑了运动参数限制和以单部干扰机为主的情况，提出以航迹关联准则为参考设定虚假航迹的方法，在此基础上推导ECAV运动参数和干扰信号调制参数。文献[16]通过分析ECAV路径控制参数的动态约束条件，将产生虚假航迹的动力学模型状态和控制矢量替换为一个单自由度向量，提出了产生有限时间和无限时间的虚假航迹欺骗干扰方法。

然而现有的研究工作成果缺乏考虑欺骗干扰产生的虚假目标发生机动时对于组网雷达系统滤波估计的影响分析，以及相应的欺骗干扰优化策略。ECAV编队对组网雷达实施迫近式支援欺骗干扰的目的在于产生虚假目标，诱使雷达对其进行测量和跟踪，在组网雷达融合中心形成稳定虚假航迹，维持较高的航迹精度，保证航迹不被撤销，以制造虚假空情，迷惑或误导敌方，为我方飞机突防行动创造条件。为此，本文从理论上推导了在目标机动检测约束下，虚假目标欺骗干扰对集中式组网雷达自适应滤波估计误差协方差的影响关系式，用误差协方差矩阵的迹来量化欺骗干扰效果，并以此为优化的目标函数，使用矩阵Schur补理论把约束条件转换为线性矩阵不等式，将欺骗干扰优化策略转化为求解半定规划凸优化问题。

1 组网雷达系统模型

1.1 标状态和量测方程

点迹融合数据处理结构的组网雷达基于状态变量法跟踪运动目标的状态方程[17-18]为：

Xk+1=FkXk+Vk

(1)

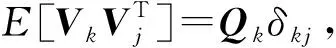
(2)

因此过程噪声在不同时刻是相互独立的。假定组网雷达系统中有N部雷达跟踪同一目标，第i部雷达在k时刻的量测方程[19-20]为：

(3)

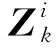
1.2 适应滤波

记N部集中式组网雷达总的量测[21]为：

(4)

其中

(5)

组网雷达系统跟踪机动目标的自适应卡尔曼滤波基本方程[22-23]如下所示。

状态预测方程：

(6)

预测估计值协方差矩阵：

(7)

增益矩阵：

(8)

滤波估计值：

(9)

滤波估计值协方差矩阵：

Pk|k=Pk|k-1-KkHkPk|k-1

(10)

残差向量：

(11)

其均值E[dk]=0。

协方差矩阵：

(12)

为便于分析，引入Lyapunov和Riccati运算符f1，f2。

f1(X)=FXFT+Q

(13)

f2(X)=X-XHT(HXHT+R)-1HX

(14)

滤波误差协方差稳态值表示为：

(15)

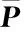
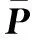
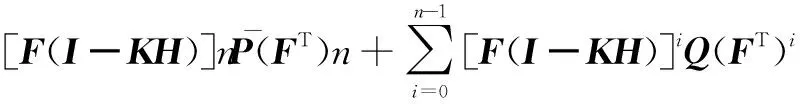
(16)

相应地，滤波估计增益稳态值为：

(17)

机动检测自适应算法不依赖于目标机动的先验假设，机动看成是目标动态特性的内部变化，而不是状态噪声方差的加入。由于残差序列dk是零均值和协方差为Sk的独立同分布高斯随机变量，所以检测手段采用基于残差的χ2检测器。

检测器基于稳态残差协方差矩阵Sk归一化的残差平方和距离函数，在k时刻，检测准则[26]为：

(18)

其中：L为检测窗口大小；ε为阈值大小；原假设H0表示目标没有机动；备择假设H1表示目标发生机动；μk满足自由度为m的χ2分布。如果μk大于等于阈值ε，则认为目标发生了机动。

2 欺骗干扰原理、模型及影响分析

2.1 欺骗干扰原理

ECAV编队对组网雷达实施欺骗干扰的原理如图1所示，每架ECAV配备的数字射频存储器(Digital Radio Frequency Memory，DRFM)可以接收、调制并转发雷达的发射信号，ECAV截获雷达发射的脉冲信号，对其进行调制延迟转发，使得欺骗干扰信号进入雷达并形成虚假目标点。通过控制虚假目标相对于雷达的回波时延，就可以在雷达与ECAV连线的延长线上指定位置产生虚假目标，随着ECAV以一定方式运动，雷达探测到的虚假目标也随之发生运动，累积的虚假目标点迹形成虚假目标航迹[27]。

由图1可知，ECAV编队对组网雷达实施欺骗干扰还需要满足以下前提条件：①ECAV必须处在雷达与虚假目标的连接视线(Line Of Sight, LOS)上，保证每架ECAV对一部雷达实施欺骗干扰；②ECAV平台小型化，不易被敌方雷达侦察到，确保完成整个干扰流程；③ECAV侦察引导设备灵敏度使其足以接收到雷达信号并精确测量其参数，ECAV装备的DRFM可以快速识别调制转发所接收的雷达信号[11]。

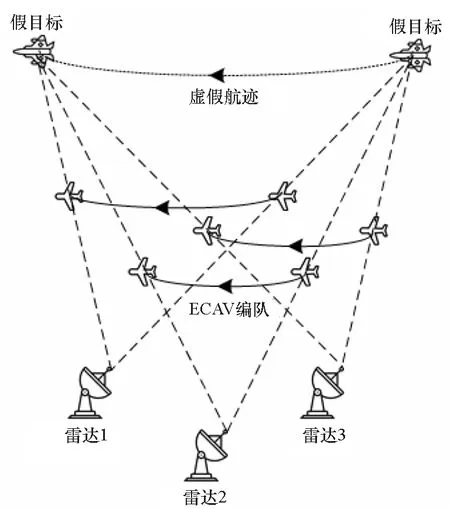
图1 对组网雷达实施航迹欺骗干扰Fig.1 Phantom track deception jamming against netted radar

雷达、ECAV和假目标的空间位置关系如图2所示。图2中：点O表示雷达的位置；点A和点B表示ECAV和假目标的当前位置；点C和D表示ECAV和假目标的下一位置；α为假目标运动方向与雷达和假目标连线方向的夹角；β为ECAV运动方向与雷达和假目标连线方向的夹角。

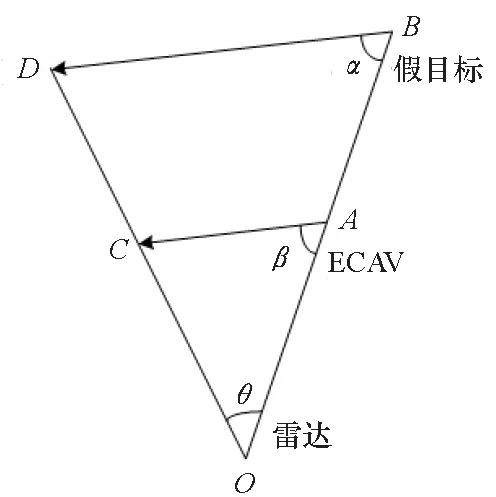
图2 位置关系Fig.2 Position relation

2.1.1 距离时延

假设ECAV与雷达的距离为r0，设定比该ECAV径向距离更远的虚假目标与雷达的距离为rf，那么虚假目标较ECAV的回波时延为:

τ=2(rf-r0)/c

(19)

式中，c为光速。由ECAV编队对组网雷达实施欺骗干扰的原理可知，在整个过程中首先得到的是假目标点迹的参数和ECAV的当前位置，即图2中OA、OB和BD是已知的，需要求解的是ECAV的下一位置OC。如图2所示，在△OBD中，根据余弦定理可以求得：

(20)

在△OAC中，根据正弦定理可以求得：

(21)

将式(21)代入式(1)可得：

(22)

从上述计算过程可以得知，在给定虚假目标航迹后，能够通过递推计算得到ECAV的运动特征参数，只要ECAV按此方式运动并逐步实施欺骗干扰就能形成相应的虚假航迹[15]。

2.1.2 多普勒频移

雷达系统有很多方法对跟踪目标进行测速，最常用的就是脉冲多普勒频移测速法，它测量雷达发射信号频率与回波信号频率的差值fd，该频率差值即为多普勒频率。相邻两次欺骗干扰之间的时间间隔设为Δt0，假定ECAV在干扰点处的速度为其在间隔Δt0内匀速运动的速度，则可以求出假目标和ECAV的运动速度为:

(23)

(24)

虚假目标应有的多普勒频率为：

(25)

式中，λ为雷达发射信号的波长。

对于位置固定式雷达，ECAV的多普勒频率为f0。如果要产生指定速度大小的虚假目标，既要给虚假目标设定相应的多普勒频率fd，也要抵消ECAV自身的多普勒频率。所以ECAV需要调制的多普勒频率参数为：

(26)

2.2 欺骗干扰模型

假设ECAV编队对组网雷达系统发起欺骗干扰，其目标是降低雷达组网系统对于运动目标的滤波估计性能。受攻击的雷达接收到一个时延发生改变的虚假回波信号，从而得到有偏差的量测数据[28-29]：

(27)

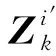
于是量测变为：

(28)

式中，i∈u为未受到欺骗攻击的雷达，i∈υ为受到欺骗攻击的雷达。

此时残差可以写为：

d′k=Gkdk+ak

(29)

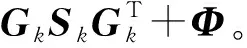
(30)

(31)

2.3 欺骗干扰影响分析

组网雷达系统的状态预测方程和滤波估计在受到欺骗干扰后变为：

X′k|k-1=FkX′k-1

(32)

X′k=X′k|k-1+Kkd′k

(33)

因为满足式(31)约束的欺骗干扰产生的残差可以通过机动检测，所以滤波估计值会显著偏离真实值。根据欺骗干扰前后的目标状态方程和滤波估计可得：

Xk-X′k|k-1=Fk(Xk-1-X′k-1)+Wk-1

(34)

Xk-X′k=Xk-X′k|k-1-Kkd′k

(35)

进而滤波估计的误差协方差变为：

P′k|k-1=E[(Xk-X′k|k-1)(Xk-X′k|k-1)T]

(36)

P′k=E[(Xk-X′k)(Xk-X′k)T]

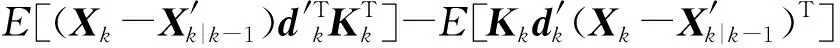
(37)

为计算式(37)的最后两项，首先计算：

Xk-X′k|k-1=FXk-1+Wk-1-F(X′k-1|k-2+Kd′k-1)

(38)

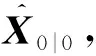
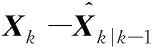
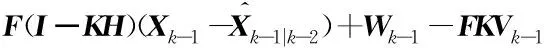
(39)

于是d′k可表示为：

d′k=Gkdk+ak

GkHwk-1-GkHFKVk-1+GkVk+ak

(40)

此时式(37)的倒数第二项可以写为：

E[(Xk-X′k|k-1)d′TkKT]

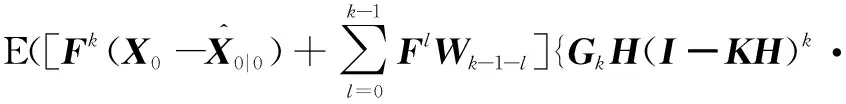
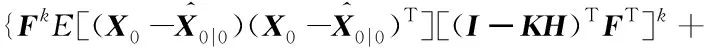
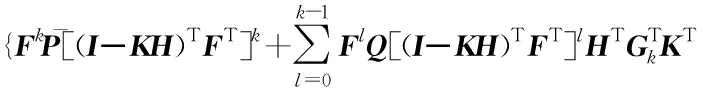
(41)

同理可得：

(42)

综上所述，将式(41)和式(42)代入式(37)中，可得欺骗干扰后的滤波估计误差协方差为：

(43)

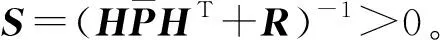
3 欺骗干扰优化策略

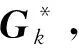
(44)

由tr(A+B)=tr(A)+tr(B)，tr(ABCD)=tr(DABC)和tr(XTY)=tr(XYT)，可得：

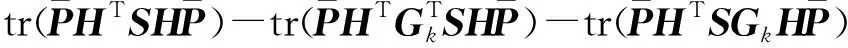
(45)

其中，S和P为半正定矩阵。

忽略式(45)最后一个等式中的常量，最优欺骗干扰策略等价于求解以下最优化问题。

(46)

为求解上述优化问题，使用矩阵Schur补理论来把约束条件转换为线性矩阵不等式。

(47)

这样欺骗干扰优化策略就转化为求解半定规划凸优化问题。基于前文的分析推导，针对自适应滤波的组网雷达欺骗干扰优化策略实施过程为：

1)干扰侦察，获得敌方雷达的发射信号波形、信号强度和脉冲重复周期等先验信息；

2)设定虚假航迹信息，设计出满足组网雷达点迹关联准则的虚假目标，对组网雷达实施航迹欺骗干扰的ECAV编队在满足基本的空间几何约束和动力学约束条件[11,15]的同时，转发的虚假目标信号量测的残差还应该满足式(47)求解出的线性系数矩阵；

3)在对ECAV自身状态进行测量的基础上，依据第2节分析的欺骗干扰原理递推计算ECAV自身运动参数，并逐步实施干扰；

4)干扰任务结束。

4 仿真分析

假设有3部雷达进行组网，其中雷达1作为坐标原点，以此建立笛卡尔直角坐标系，存在3架ECAV在组网雷达探测范围内飞行。仿真时间长度为300 s，ECAV分别对每一部雷达发起假目标欺骗干扰，欺骗干扰参数根据上文所述凸优化问题，利用MATLAB中的CVX工具箱进行求解。其中，3部组网雷达的各项参数见表1。

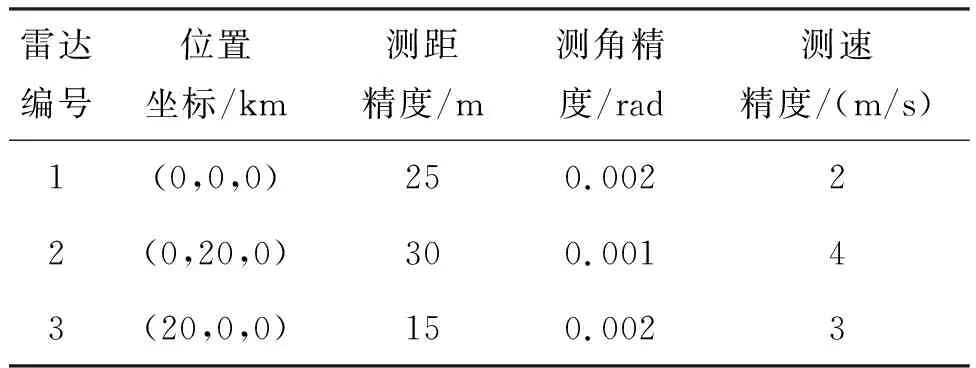
表1 组网雷达参数

每一部雷达独立进行信号处理和点迹录取，然后将数据传送给组网雷达融合中心。融合中心首先进行误差配准，对不同的雷达进行系统误差校正；然后进行坐标变换，将来源于不同雷达的量测数据转换到同一个坐标系下(数据融合处理中心坐标系)，并采用概率数据互联算法进行数据关联、同源检验；最后进行自适应滤波估计，实现对目标的跟踪。

4.1 虚假目标不发生机动

在本节的仿真情景下，3架ECAV分别对3部组网雷达进行欺骗干扰，产生的虚假目标不发生机动且做匀速运动，此时的状态转移矩阵[30]为：

Fcv=diag(Acv,Acv,Acv)

(48)

(49)

式中，ΔT为雷达采样时间间隔，取为1 s；设定的虚假目标航迹和欺骗干扰优化前后分别产生的虚假目标滤波航迹如图3所示。组网雷达融合中心在欺骗干扰优化前后的滤波估计误差协方差矩阵的迹如图4所示。

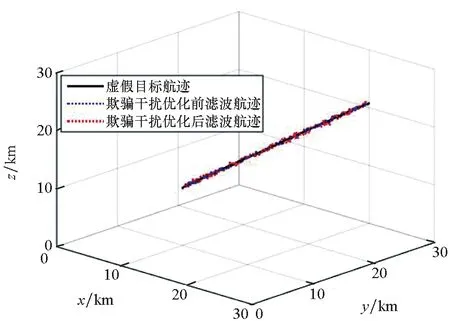
图3 匀速虚假目标的航迹Fig.3 Flight path of false target with constant velocity

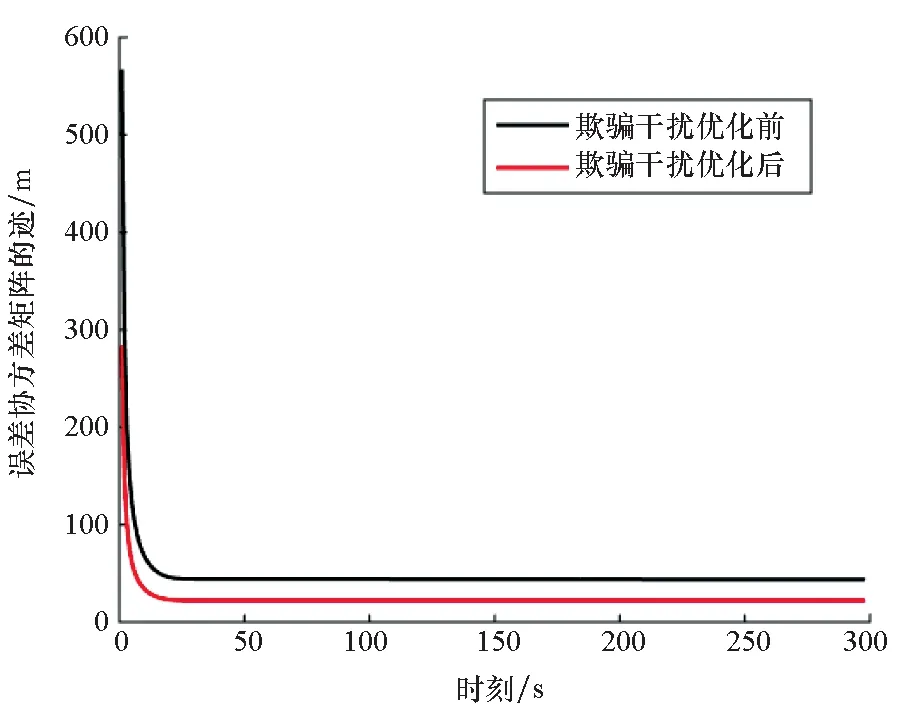
图4 误差协方差矩阵的迹(虚假目标不发生机动)Fig.4 Trace of error covariance matrix(false targets don′t occur in manoeuvres)

当虚假目标不发生机动且做匀速运动时，采用优化后的欺骗干扰策略对组网雷达进行干扰后，滤波估计误差协方差矩阵的迹小于优化前的迹，即虚假航迹精度更高，欺骗干扰效果更好。误差协方差收敛速度基本不受影响，本文所提的欺骗干扰优化策略在产生的虚假目标不发生机动时也有效。

4.2 虚假目标发生机动

在本节的仿真情景下，3架ECAV分别对3部组网雷达进行欺骗干扰，产生的虚假目标发生机动且做匀加速运动，此时的状态转移矩阵[30]为：

Fca=diag(Aca,Aca,Aca)

(50)

(51)

式中，ΔT为雷达采样时间间隔，取为1 s。设定的虚假目标航迹和欺骗干扰优化前后分别产生的虚假目标滤波航迹如图5所示。

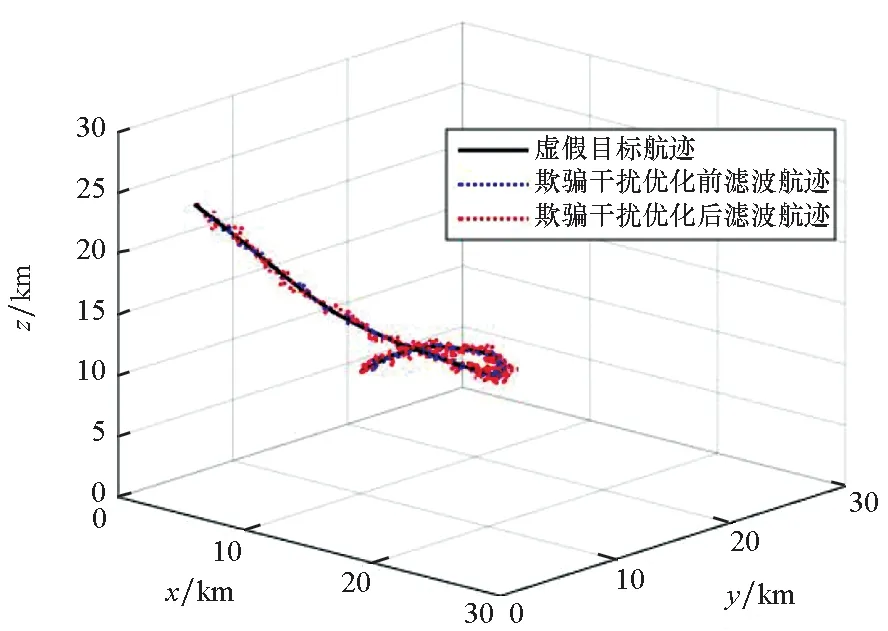
图5 匀加速虚假目标的航迹Fig.5 Flight path of false target with constant acceleration

当虚假目标发生机动且做匀加速运动时，欺骗干扰优化前后的残差平方和距离函数值如图6和图7所示。采用优化前的欺骗干扰策略产生的机动虚假目标残差平方和距离函数值μk多数大于机动检测阈值，被组网雷达检测出机动状态；而优化后的欺骗干扰策略产生的机动虚假目标残差平方和距离函数值基本小于机动检测阈值，没有被组网雷达检测出机动状态。

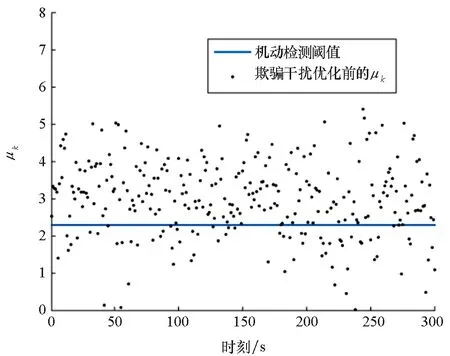
图6 欺骗干扰优化前的μkFig.6 μk before optimized deception jamming

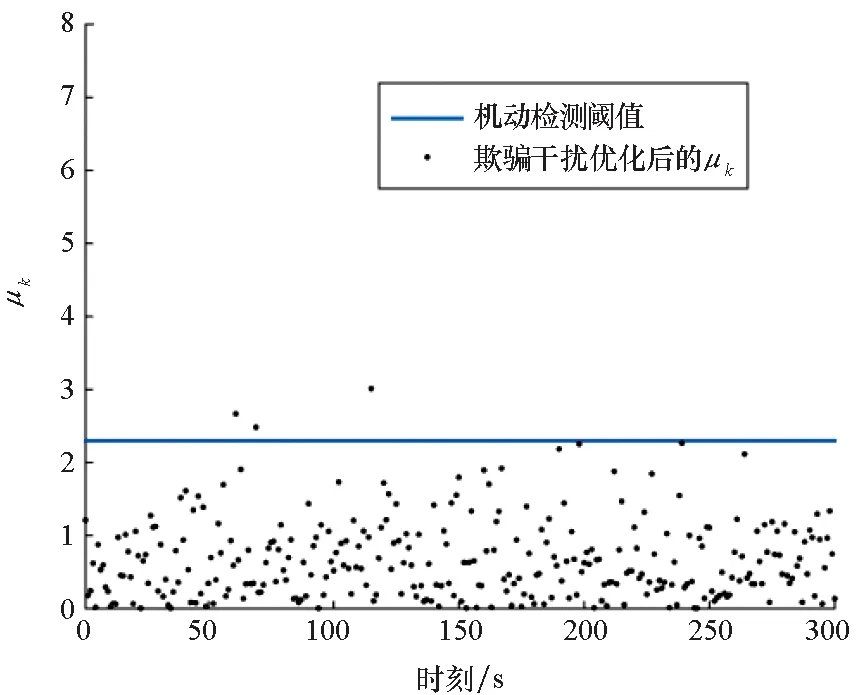
图7 欺骗干扰优化后的μkFig.7 μk after optimized deception jamming

组网雷达融合中心在欺骗干扰优化前后的滤波估计误差协方差矩阵的迹如图8所示。当虚假目标发生机动且做匀加速运动时，采用优化后的欺骗干扰策略对组网雷达进行干扰后，滤波估计误差协方差矩阵的迹小于优化前的迹，即虚假航迹精度更高，欺骗干扰效果更好。并且在收敛后要大于非机动时的迹，这是因为组网雷达未检测出优化后欺骗干扰策略产生的虚假目标机动状态，而仍然采用匀速模型滤波，仿真结果证明了欺骗干扰优化策略的有效性。

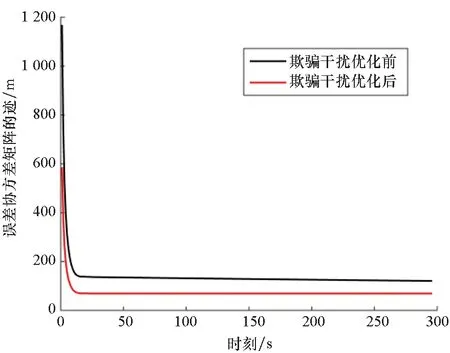
图8 误差协方差矩阵的迹(虚假目标发生机动)Fig.8 Trace of error covariance matrix(false target maneuvers)

5 结论

在组网雷达对抗中，能够产生稳定航迹的欺骗干扰策略是一种有力的干扰手段。本文从理论上推导了在目标机动检测约束下，虚假目标欺骗干扰对集中式组网雷达自适应滤波估计误差协方差的影响关系式，然后用误差协方差矩阵的迹来量化欺骗干扰效果，将欺骗干扰优化策略转化为求解半定规划凸优化问题。对于分布式和混合式结构组网雷达系统的欺骗干扰优化策略还需要进一步的研究。