湘教版与人教A版高中数学建模内容比较研究
吴文斌 王洁 张炳意
【摘要】文章采用内容分析法和比较法,分析比较了湘教版和人教A版高中数学建模内容的异同,发现湘教版注重函数模型的综合应用,数学建模专题注重建模活动的逐次开展,人教A版注重函数模型的直接应用,数学建模专题注重建模活动的整体开展;湘教版侧重选择与学生联系密切的生活问题情境,人教A版侧重选择与数学联系密切的科学问题情境;湘教版注重陈述句与开放式相结合的问题表述形式,人教A版注重疑问句与封闭式相结合的形式;湘教版重视自主发现问题和选择数学模型解决问题,人教A版注重分析问题和应用已给模型解决问题。基于此,对湘教版建模内容提出整体把握数学建模活动的不同侧重点,统整资源,选择适合数学建模活动的情境与问题,整体设计突出数学建模活动的层次性,注重数学建模过程的完整性与活动性的使用建议。
【关键词】湘教版;人教A版;数学建模;框架;分析建议
【中图分类号】G633.6【文献标志码】A【文章编号】1004—0463(2022)05—0066—06
《普通高中数学课程标准》(2017年版)指出,数学建模能力是六大核心素养之一,并提倡教师要将数学建模活动与数学探究活动确定为高中数学课程内容的一条主线。依据《普通高中数学课程标准》(2017年版)编写的高中数学教科书已经投入使用,数学建模内容的体例结构、编写特色等是数学教师关注的问题,因此,有必要深入比较研究数学建模内容,为一线教师解读建模内容、整合建模资源、开展建模教学提供参考。
选取2019年湖南教育出版社出版的普通高中数学必修教科书(简称湘教版)和人民教育出版社出版的普通高中数学必修教科书(简称人教 A版)为研究文本,以两版教科书中数学建模内容为研究对象。
课程标准将数学建模素养定义为“对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养”,数学建模过程主要包括“在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型。”理解数学建模要把握三大要义,一是解决现实问题;二是将现实问题通过数学抽象转化为数学问题;三是要经历完整的建模过程。基于已有研究的分析框架,依据课程标准提出的概念框架,将数学建模内容分析框架确定为:内容分布、情境类型、问题表述、建模过程。
(一)内容分布
为了便于研究,只选取显性形式呈现的建模内容进行分析,也就是教科书中带有明显的“模型”或“建模”文字表述的章节,从数学建模内容的呈现位置、建模问题数量、建议课时和页数四个指标进行统计,其中建模问题是指教科书中符合数学建模要求的现实问题,这些问题通常以案例、例题、练习、习题、阅读的形式呈现。内容分布情况如表1所示。
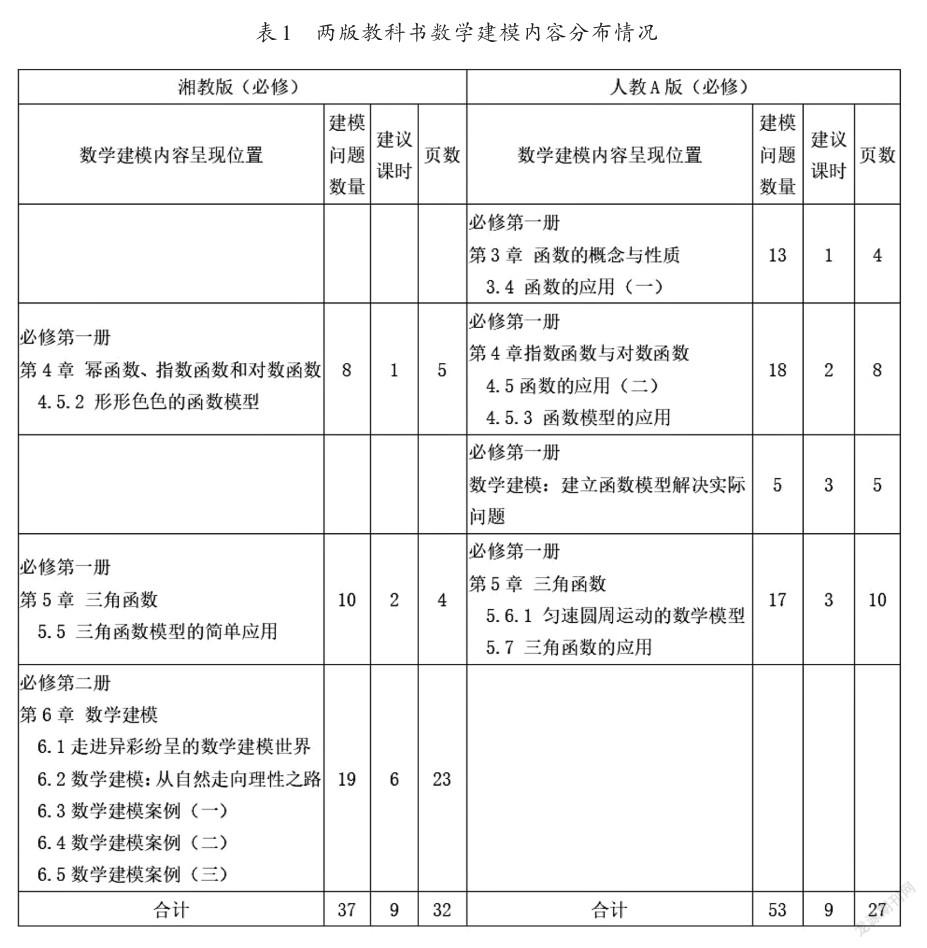
由表1可知,两版教科书都在必修第一册函数主题部分设置了“函数模型应用”,但在内容呈现位置、课时方面均有差异。湘教版“函数模型应用”分布在第4、5章,有9页内容,共包含18个建模问题,计划3课时。其中“4.5.2形形色色的函数模型”先给出了数学建模的定义和数学建模的四个步骤,然后通过实例,让学生学会选择合适的函数模型刻画现实问题的变化规律;“4.5.5节三角函数模型的简单应用”,选用简谐振动(单摆)和匀速圆周运动两个实例说明三角函数模型在实际问题中的应用。人教A版“函数模型应用”分布在第3、4、5章,有19页内容,共包含48个建模问题,计划6课时。其中“3.4函数的应用(一)”通过一些实例学习一次函数、二次函数、幂函数模型解决实际问题的过程和方法;“4.5.3函数模型的应用”结合四个实例,学习运用模型思想选择恰当的函数模型刻画不同的变化规律;5.6节学习利用三角函数知识刻画“匀速圆周运动的数学模型”,“5.7节三角函数的应用”选用简谐振动(弹簧振子)和交变电流两个具体实例,说明三角函数模型的简单应用。
两版教科书都设置了“数学建模专题”,但在内容呈现位置、建模问题数量方面均有差异。湘教版“数学建模专题”安排在必修第二册中,独立成章,包括5小节内容,有23页共19个建模问题,计划6课时。5节内容主要包括数学模型及其作用、数学建模活动的基本过程、建立数学模型解决现实问题的全过程等。人教A版“数学建模专题”安排在必修第一册中,没有独立设章,有5页内容含5个建模问题,计划3课时。内容以函数建模实例展现了构建数学模型解决实际问题的过程,给出了数学建模活动指导。
由以上梳理可知,湘教版与人教A版均在函数主题中设置了“函数模型应用”渗透建模思想,单独设置了“数学建模专题”开展数学建模活动。两版教科书在内容编排上各有特点,在“函数模型应用”上,湘教版注重渗透数学建模过程,强调函数模型的综合应用;人教A版注重渗透数学建模思想,强调函数模型的直接应用。在“数学建模专题”上,湘教版注重数学建模活动的逐次开展,内容编排系统完整、案例丰富;人教A版注重数学建模活动的整体开展,内容编排紧凑、选题丰富。
(二)情境类型
“情境类型”是指教科书在组织和呈现数学建模问题时所使用的现实情境类型,依其来源可分为个人情境、社会情境、职业情境和科学情境。统计两版教科书中数学建模问题情境类型,如表2所示。
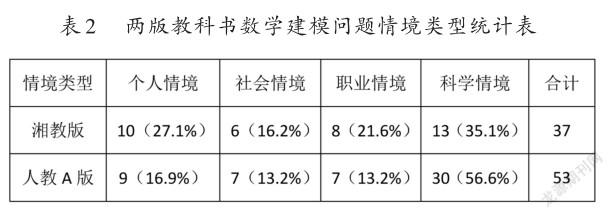
由表2可知,两版教科书建模问题选用科學情境的比例最大,而且人教A版高于湘教版。进一步分析发现,两版教科书在科学情境选材上有差异:湘教版科学情境选材主要集中在物理情境上,重视数学与物理学的联系,如单摆运动、匀速圆周运动、交变电流、万有引力定律、自由落体运动等,让学生体会用数学解决物理问题的实质;人教A版科学情境选材涉及学科较多,包括物理学、化学、生物学、医学、天文学、心理学、环境科学、计算机科学情境,这表明人教A版建模问题情境类型多样,注重数学与其他科学的联系,能较好地体现数学的广泛应用性。另外,湘教版设计的个人情境、社会情境、职业情境建模问题比例均高于人教A版,表明湘教版教科书注重选择与学生实际生活密切相关的情境,如最佳射门、蜂房结构、估计产量等案例。
以上分析表明,虽然两版教科书建模问题情境以科学情境为主,但在情境选择上各有侧重,湘教版侧重选择与学生联系密切的生活问题情境,而人教A版侧重选择与数学联系密切的科学问题情境。
(三)问题表述
现实问题的不同表述形式影响数学建模活动的开放程度。问题表述包括提出问题时所用的句式和所提问题的类型。其中,问题句式包括陈述句和疑问句,陈述句是直接陈述一个数学事实、任务或活动要求,句末一般用句号表示;疑问句用询问或者反问等方式表述数学任务或活动要求,句末一般用问号表示。问题类型分为封闭式和开放式,封闭式的答案和解答方法唯一,开放式没有预设的结论,所得结论是多元的,或者没有规定学生使用某种方法或策略解决问题,其过程是多元的[1]。统计两版教科书建模问题的表述形式,如表3所示。
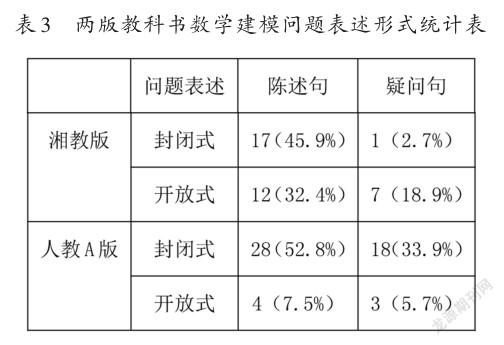
由表3可知,从单一维度看,两版教科书建模问题以陈述句为主,但湘教版建模问题的陈述句表述比例高于人教A版;湘教版开放式建模问题比例远高于人教A版,人教A版封闭式建模问题比例远高于湘教版。从双重维度看,湘教版建模问题以“陈述句+开放式”形式表述的比例明显高于人教A版,人教A版建模问题以“疑问句+封闭式”形式表述的比例明显高于湘教版。
以上分析表明,湘教版建模问题表述形式注重“陈述句”与“开放式”的结合,这种表述形式使建模问题的条件和结论比较隐蔽,更符合数学建模的特征。人教A版建模问题表述形式注重“疑问句”与“封闭式”的结合,这种表述使数学问题更加明确,突出数学应用的特征。
(四)建模过程
建模过程是把现实世界中的实际问题提炼、抽象为数学模型,求出数学模型的解,验证数学模型的合理性,并用数学模型提供的结论揭示实际问题的一种数学应用过程[2]。过程性是数学建模活动的核心要义,完整的数学建模过程包括五步:实际情境—提出问题与分析问题—建立模型与求解模型—检验结果—模型修正。本研究将这五步作为建模过程要素分析的步骤。第一步从情境的现实性进行分析;第二步从提出问题的方式和是否有详细分析过程进行分析;第三步从数学模型是否已知进行分析;第四步从是否有模型检验过程进行分析;第五步从是否有模型修正过程进行分析。
本研究只选取“建立模型与求解模型”过程的建模问题为研究对象,比较分析两版教科书筛选出23个建模问题,其中湘教版有10个,人教A版有13個。数学建模过程要素分析如表4所示。
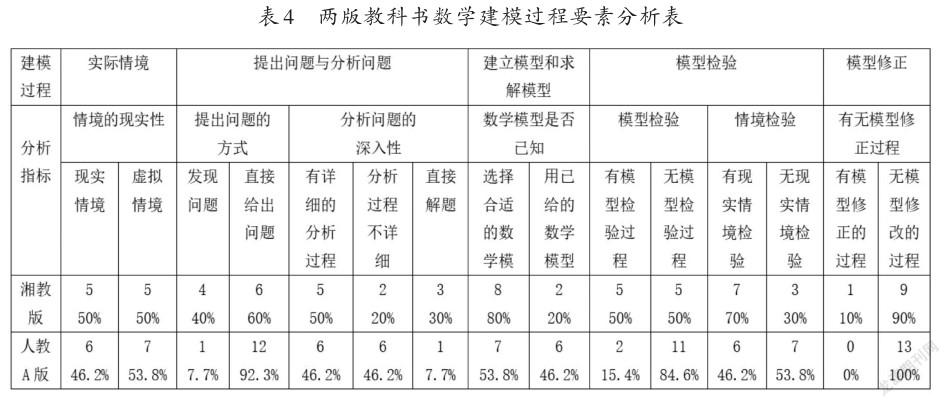
由表4可知,湘教版建模问题的现实情境与虚拟情境数量比例均为50%,人教A版建模问题虚拟情境比例略高于现实情境;湘教版采用发现问题方式的比例高于人教A版,人教A版采用直接给出问题方式的比例明显高于湘教版;湘教版有详细分析过程的建模问题比例略高于人教A版,有分析过程但不详细的建模问题比例人教A版高于湘教版;两版教科书半数以上的建模问题需要选择合适的数学模型,湘教版与人教A版的比例分别为80%、53.8%,但人教A版有46.2%的建模问题是用已给的数学模型解决问题,湘教版这一比例仅为20%;湘教版有50%的建模问题有模型检验过程,且有70%的建模问题将结论带入现实情境以检验模型的合理性,人教A版84.6%的建模问题无模型检验过程,且53.8%的建模问题无现实情境的分析;两版教科书中只有湘教版有一个建模问题有模型修正,其余建模问题均无模型修正过程。
此外,课程标准强调数学建模活动以课题研究的形式开展,但两版教科书只在数学建模专题部分提到了课题研究,其他建模问题几乎没有提及课题研究。进一步对比发现,人教A版课题研究过程包括选题、开题、做题、结题,与课程标准要求一致,湘教版课题研究出现在练习题中,但无选题、开题的过程。
从以上分析可以看出,两版教科书建模问题过程要素基本齐全,但在具体过程中处理方式有差异。湘教版比较重视以发现的方式提出问题,绝大多数建模问题需要学生自主选择合适的数学模型解决问题,半数以上的建模问题有模型检验的过程且关注到模型修正过程;人教A版直接给出问题提出的主要方式,绝大多数建模问题有分析过程,40%以上建模问题是用已给的数学模型解决问题,半数以上的建模问题无模型检验过程,模型修正过程关注不够,课题研究过程相对完整。
(一)结论
1.内容分布。湘教版“函数模型应用”注重渗透数学建模过程,强调函数模型的综合应用,“数学建模专题”注重数学建模活动的逐次开展,内容编排系统完整、案例丰富;人教A版“函数模型应用”注重渗透数学建模思想,强调函数模型的直接应用,“数学建模专题”注重数学建模活动的整体开展,内容编排紧凑、选题丰富。
2.情境类型。湘教版侧重选择与学生联系密切的生活问题情境;人教A版侧重选择与数学联系密切的科学问题情境。
3.问题表述。湘教版注重“陈述句”与“开放式”相结合的表述形式,符合数学建模特征,注重发展学生的“四能”;人教A版注重“疑问句”与“封闭式”相结合的表述形式,突出数学应用特征,强化学生的“双能”。
4.建模过程。湘教版比较重视以发现的方式提出问题,注重学生自主选择合适的数学模型解决问题,关注模型检验与修正过程;人教A版主要采用直接给出问题的方式,注重建模问题的分析过程,主要用已给的数学模型解决问题,对模型检验修正过程关注不够。
(二)建议
基于上述分析与结论,对湘教版教科书使用提出以下建议。
1.整体把握不同类型数学建模活动的目标要求。函数模型应用侧重于局部的数学建模活动,重在数学应用意识的渗透,数学建模专题要突出运用数学知识解决现实问题的过程,侧重建模过程的体验。教学中应整体把握不同类建模活动的目标要求,力争重要的概念有背景,重要的结果有应用,让学生从模仿应用到自主参与数学建模活动全过程。
2.选择适合数学建模活动的情境与问题。建模问题不同于应用题,建模问题情境选择应尽量保留其“现实性”和“多样性”,不易做过多的简化与假设,否则学生缺乏对问题的分析和假设过程的经历,数学建模水平很难得到提高。建模问题的选择要贴近学生生活和实际,条件和结论应该隐蔽在背景中,可用信息和最终结论让学生自己去挖掘。因此,教师需要统整不同版本教科书内容,为学生选择适合的数学建模情境与问题。
3.整体设计数学建模活动的教学。数学建模素养的养成需要一个渐进的过程,湘教版在各章内容中均渗透数学建模活动。教学中要依据单元教学理论,以数学建模素养发展的三级水平为依据,整体地、有层次地、逐步地深入开展数学建模活动。要将教学重点放在数学建模专题上,为学生创造有利的时空条件,真正开展完整的数学建模活动。
4.注重数学建模过程的完整性与活动性。数学建模专题活动的开展,应选择建模过程相对完整的问题情境,重视学生自己发现问题和提出问题的过程,自主选择合适的数学模型解决问题的过程以及模型检验与模型修正的过程。数学建模活动应以课题研究的形式开展,让学生经历从选题、开题、做题到结题的完整过程,注重培养学生的建模素养及团队合作能力。
[1]徐斌艳.高中数学教科书探究内容的分析指标体系及比较研究[J].课程·教材·教法,2012(10):36.
[2]邵光华,蒋周渠.数学建模素养评价模型与案例分析[J].中国数学教育,2020(08):4.
编辑:徐春霞

