十种方法求角的内角平分线所在直线方程

钟建新

(浙江省春晖中学 312300)

题目已知△ABC三个顶点A(2,5)，B(6,8)，C(8,-3)，求∠A的内角平分线所在的直线方程.

解法1由题意得，∠A的内角平分线所在的直线有斜率，下设∠A的内角平分线所在的直线l方程为

y-5=k(x-2)，

点B(6,8)关于l的对称点为B′(a,b)，

则点B′(a,b)在直线

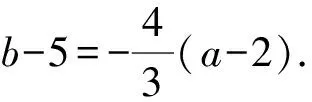
①

又线段BB′中点在l上，

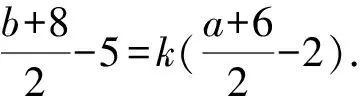
②

且kBB′·kl=-1，

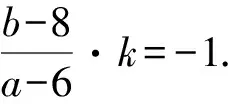
③

以上三式联立可解得

所以直线l方程为

即∠A的内角平分线所在的直线方程为

x+7y-37=0.

解法2设点B(6,8)关于∠A的内角平分线所在直线l的对称点为B′(a,b)，

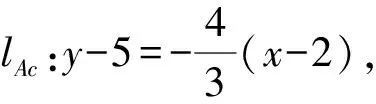
④

又|AB′|=|AB|，

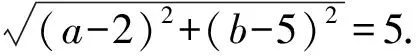
⑤

以上两式联立可解得

a=5,b=1.

所以B′(5,1)，kBB′=7.

又kBB′·kl=-1，

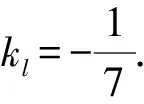
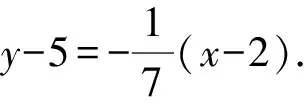
即∠A的内角平分线所在的直线方程为

x+7y-37=0.

解法3设点P(x,y)为∠A的内角平分线所在的直线上任意一点，则点P到边AB和边AC的距离相等.

即lAB:3x-4y+14=0.

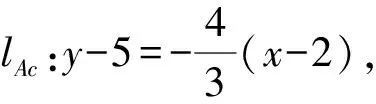
即lAc:4x+3y-23=0.

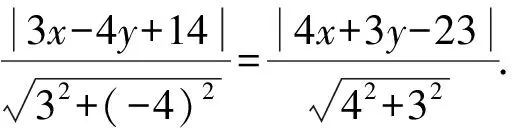
所以3x-4y+14=4x+3y-23，

或3x-4y+14=-(4x+3y-23).

即x+7y-37=0，或7x-y-9=0.

因为直线7x-y-9=0为∠A的外角平分线所在的直线，故舍去.

所以∠A的内角平分线所在的直线方程为

x+7y-37=0.

设∠A的内角平分线所在的直线的斜率为k，则用到角公式得

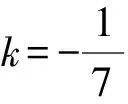
所以∠A的内角平分线所在的直线方程为

x+7y-37=0.

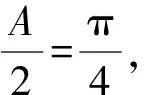
下设∠A的内角平分线所在的直线的斜率为k，则用到角公式得：

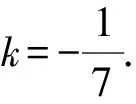
所以∠A的内角平分线所在的直线方程为

x+7y-37=0.

解法6 若lAB:A1x+B1y+C1=0，

lAc:A2x+B2y+C2=0，

则∠A的内角平分线和其外角平分线所在的直线方程各为以下之一：

(A1x+B1y+C1)-λ(A2x+B2y+C2)=0,

或(A1x+B1y+C1)+λ(A2x+B2y+C2)=0，

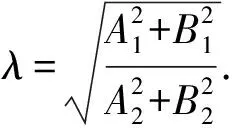
该结论可通过点线距相等来证明.

结合本题题意，因为

lAB:3x-4y+14=0，

lAc:4x+3y-23=0，

所以∠A的内角平分线和其外角平分线所在的直线方程各为以下之一：

(3x-4y+14)-λ(4x+3y-23)=0,或

(3x-4y+14)+λ(4x+3y-23)=0，

所以整理，得

x+7y-37=0，或

7x-y-9=0(舍去).

所以∠A的内角平分线所在的直线方程为

x+7y-37=0.

解法7 因为

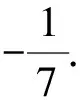
所以∠A的内角平分线所在的直线方程为

x+7y-37=0.

解法8 由题意，|AB|=5，|AC|=10.

设∠A的内角平分线与边BC的交点为D，

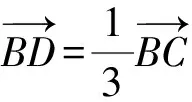
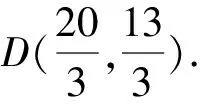
又A(2,5)，

直线AD的方程为x+7y-37=0.

即∠A的内角平分线所在的直线方程为

x+7y-37=0.

解法9 设点P(x,y)为∠A的内角平分线所在的直线上任意一点，则

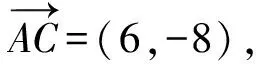
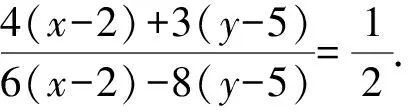
化简,得x+7y-37=0.

所以∠A的内角平分线所在的直线方程为

x+7y-37=0.

化简,得x+7y-37=0.

所以∠A的内角平分线所在的直线方程为

x+7y-37=0.

一题多解，能提升学生的解题能力，达到事半功倍的效果，这也是培养、发展其核心素养的重要路经.通过对以上10种解法的探析比较，可以巩固学生所学知识，扩展数学思维，开拓数学视野，最终达到提升其自身数学核心素养的目的.