新高考数学多选题的知识点分析与解题策略

张诗萍 谢加良 李 凤

(福建省集美大学 361021)

谢加良(1981-)，教授,从事数据分析与挖掘、数学教育学等.

李凤(1980-)，副教授，从事不确定性的数学理论、数学建模研究.

新课标下的高考以立德树人为根本任务，以科学评价人才为主要使命，实现全面发展的育人目标.新高考实行文理不分科的改革措施，并对统考科目提出了新定位和区分选拔的要求.因此，为了突出数学考试的新定位和科学评价功能，实现区分考生的目的，新高考数学增加了多选题这一创新题型.新高考数学多选题虽然不需要学生写出解题步骤，但是考查知识点众多，需要考生具备良好的数学逻辑和清晰的解题思路，以此实现多层次区分的目的.因此，多选题对学生的数学双基能力考查更加深入，对学生的数学思维、数学逻辑要求也更严格.

本文在研究数学新高考与旧高考的过程中，发现最大的区分点是新高考增加了多项选择题部分，由12道单选题，变成“8+4”(8道单选与4道多选)模式.学生做答多选题会形成两极分化，成绩优异的学生能做出来，成绩一般的学生不容易做出来；新高考增加的多选题能大幅度地照顾到中间层次的学生，不但有利于区分学生的学习水平，而且能提高学生的整体得分率.本文对高考卷多选题进行分析，并依次从知识点的考查，命题难度、核心素养这三个方面来分析这些多选题.根据多年解题经验总结出排除法、特殊值赋值法、保守得分法等解题策略，能为考生的复习和教师授课提供一些建议.

1 新高考多选题分析

表1

由于多选题构成要素复杂，对于运算能力、推理等方面都可能会考查.所以多选题对学生综合能力要求更高,要求考生耐心对待.通过对以上多选题试题分析，我们可以得到以下结论：

知识点的考查：多选题涉及的题型广泛，如函数与三角函数、函数与导数、立体几何、解析几何、统计与概率等类型的题型都有可能出现在多选题.函数与解析几何结合在一起考查是数学多选题的常考点，其中把它们放在最后两题考查的可能性较大.

命题难度：由于多选题涉及的知识点广泛，学生不仅需要具备分析问题、解决问题的能力，且需要对必备知识点的概念掌握透彻才能正确解答.由此可见，多选题命题的重点变化不大，但总体难度在降低.

核心素养：多选题一题对应多个正确选项，考查多个知识点且考查学生对知识点的储备广度，对学科基础的掌握程度要求也很高，可以集中体现新高考对培养学生核心素养方面上的重视.

通过对知识点的考查，命题难度，核心素养三方面的分析可知，新高考下的多选题知识点变得更为广泛，考查难度下降，更加强调培养学生的核心素养.

2 多选题应考策略

针对八省联考以及新高考Ⅰ卷(山东)中多选题的具体选项进行分析，并根据多年解题经验针对多选题的解题方法提出以下三个策略：

2.1 特殊值赋值法

根据题干或者选项要求对变量进行特殊值赋值，从而帮助选出正确选项，也可以得到错误选项；特别地，根据多选题设置的答案个数(至少存在两个正确答案)，考生可以赋特殊值代入选项，得到错误选项，这样可以缩小范围，节约解题时间.以例1为例进行说明.

例1(2020年新高考全国Ⅰ卷(山东)9题) 已知曲线C:mx2+ny2=1,则( ).

A.若m>n>0,则C是椭圆，其焦点在y轴上

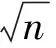
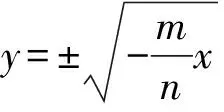
D.若m=0,n>0,则C是两条直线

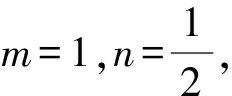
2.2 排除法

排除法指的是可以通过排除错误选项，节省学生推导和计算时间.特别地，如果考生能排除掉两个错误选项或者部分错误选项，再根据多选题设置的要求(至少存在两个正确答案)，剩下两个选项即为本题答案或者缩小解题范围，这可以提高正确率.以例2为例进行说明.

例2(2020年新高考全国Ⅰ卷(山东)10题) 图1是函数y=sin(ωx+φ)的部分图象，则y=sin(ωx+φ)等于( ).

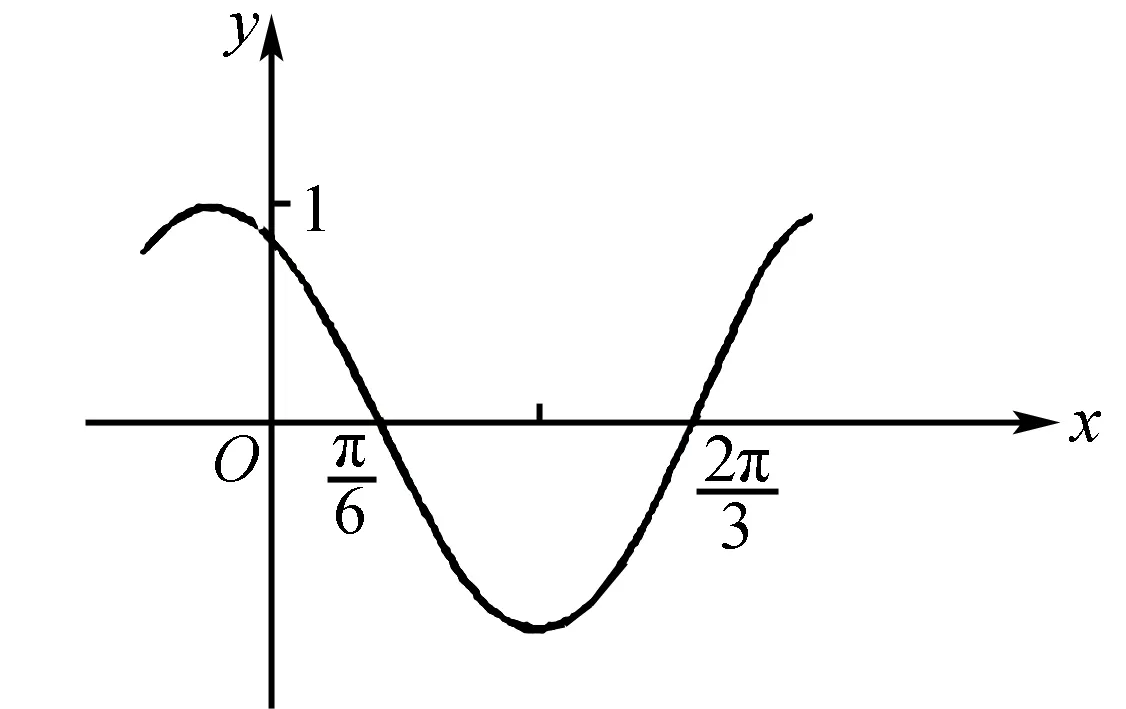
图1

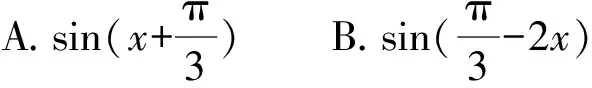
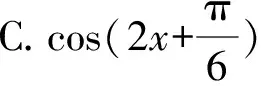
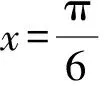
2.3 保守得分法

所谓保守得分法即根据多选题选项得分要求，全部选对的得5分，部分选对的得2分，有选错的得0分，因此，学生在没有把握的情况下可以选一个最有把握的选项，耗时少又能得到2分，即在保守情况下得到基础分；根据多年解题经验可知，多选题的答案在2至3个选项的情况下居多，因此保守得分法能保证学生拿到全部基础分.以例3为例进行说明.

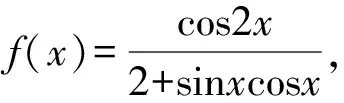
A.f(x)=f(x+π)

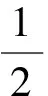
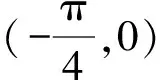
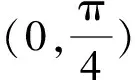
分析本题考查三角函数的性质，难度偏上，考生要得满分相对较难.但是，基础一般的同学通过计算很容易得到f(x)=f(x+π)，故知A选项正确，因此，本题运用保守得分法选A,即可得到基础分数.

由以上分析可知，作答多选题总体上如果采取保守得分法、排除法、特殊值赋值法不仅可以缩短解题时间，还可以在保证不失基础分的情况下，提高学生成绩.其中，特殊值赋值法跟排除法结合使用也是一个较好的得分策略.

3 总结与建议

新高考中的数学多选题对考生来说既是挑战也是机遇，多选题有利于区分学生的学习水平，给高校的择优提供一定的借鉴.但多个正确选项需要学生有较强的综合能力，用常规方法解答多选题，正确率要达到百分百存在一定的难度.如果适当运用多选题的解题策略就能在短时间内选出正确选项且不失基础分.因此，对学生的学习以及教师授课提出以下建议:

3.1 对于学生学习而言

掌握基础是重点，学生在备考时应该着重复习基础知识，强化计算能力；其次是整理错题、易错点，反思做错的原因；最后是研究自己的强项所在，攻薄弱的知识点，在碰到自己强项的题型务必做对，如若碰到薄弱的地方可以降低要求拿到基础分.

3.2 对于教师授课而言

教师在教学中应多给学生巩固基础，注重概念讲解，平日教学中要灌输学生数形结合、分类讨论等解题方法，在此基础上提高学生的数学成绩；在讲课过程中应多渗透数学核心素养，让学生充分了解数学建模、数学运算能力等对学好数学的重要性；培养学生良好的解题习惯，适当地运用解题策略.