与圆有关的那些“最”

南京师范大学附属中学树人学校(210000)姜红

苏科版初中教材,九年级上学期第2 章“对称图形——圆”中,有多个最值问题,值得探究.学生对此类问题的认识往往只流于浅表,未经深刻思考和推理论证,不利于思维的深度发展.针对于此,在此探究一二.

问题1 定点与定圆上点距离的最值

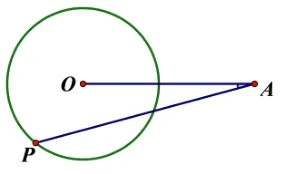
如图1,圆外点P到⊙O半径为2,OP=3,则点P到⊙O上点的最大距离为____,最小距离为____.

图1

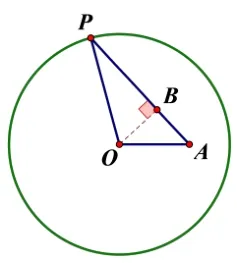
从直观上,容易意识到此问题中当点P、圆心O与圆上的点共线时,P与该点的距离取得最值.即图2 中,点P与点A距离最大,为3+2=5,与点B距离最小,为3−2=1.

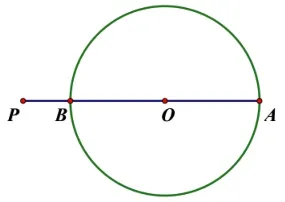
图2

但是,理由何在?

对初学者来说,还有个问题,如何证明P到某点的距离是最大的?

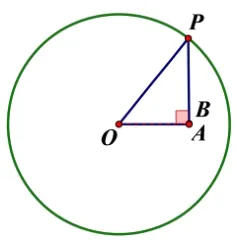
证明“P到某点的距离是最大”,即证明“P到某点的距离比P到其他点的距离都大”.故而方法可以是:在⊙O上任取另外不同于A的点A′,证明PA >PA′(如图3).具体如下:

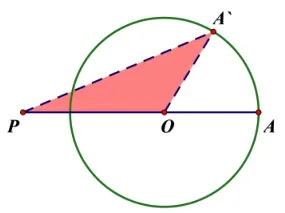
图3

在⊙O上任取另外不同于A的点A′,连接PA′、OA′.若P、O、A′三点不共线,在∆POA′中,OP+OA′ >PA′,又∵OA=OA′,∴OP+OA >PA′,即:PA >PA′.若A′在OP与⊙O的交点B处,则PA′=OP −OB=OP −OAPA′

综上,对于任意不同于A的点A′,都有PA >PA′.故点P与⊙O上点A的距离最大,为3+2=5.

同理可证,点P与⊙O上点B的距离最小,为3−2=1.故答案为:5,1

问题一般化:平面内点P到圆心O的距离为d,⊙O的半径为r.当点P在⊙O外,P到圆上点距离的最大值为d+r,最小值为d −r.当点P在⊙O内,P到圆上点距离的最大值为d+r,最小值为r −d.当点P在⊙O上,P到圆上点距离的最大值为d+r=r+r=2r,最小值为0.

综上,平面内点P到圆上点距离的最大值为d+r,最小值为|d −r|.

问题1 的变式:平面内,点P到⊙O上点的最长距离为m,最短距离为n,则此圆的半径为.

问题2 直径是圆中最长的弦

我们可以直接用上述方法加以证明.

如图4,AB为⊙O的直径,CD为任意一条非直径弦,求证:AB >CD.

图4

证明:连接OC、OD(如图5),在∆COD中,OC+OD >CD,即r+r >CD,即直径d>CD,∴直径AB >非直径弦CD.

图5

本质上讲,以上问题都是转化为“三角形的三边关系”.

问题3 过圆内定点弦长的最值

如图6,点P在⊙O内,画出过点P的最长弦、最短弦,并证明你的结论.

图6

在问题1 中已经讨论过,过点P的最长弦是直径AB.直觉感受,最短弦是跟最长弦垂直的弦CD(如图7).这个结论同样需要进行论证.以下从不同角度进行论证.

图7

方法1:垂径定理+ 勾股定理:如图8,过点P任画另一条与AB不垂直的弦EF,过点O作OG⊥EF,垂足为G,连接OC、OF.∵CD⊥AB,CD=2CP,在Rt∆OPC中,同理可得,EF=2FG,又∵OP >OG,且OC=OF,∴CP

图8

方法2:圆幂定理+基本不等式:如图9,任作弦EF与直径AB相交于点P,∴EP·FP=AP·BP=(r+d)·(r−d)=r2−d2为定值,当且仅当EP=FP时取等号.此时EF⊥AB.

图9

事实上,图7 中线段半径r(即OC)是AP与BP的算术平均数,也是Rt∆COP的斜边,而CP是AP与BP的几何平均数,也是Rt∆COP的直角边.故此图也用作对命题“两正数的算术平均数不小于其几何平均数”的证明.

问题4 定点、圆心及圆上点张角的最值

其一,定点在圆外.如图10,点A在半径为1 的⊙O外,OA=2,点B在⊙O上,则∠OAP的最大值为____.

图10

从直观上讲,当直线AP与⊙O相交时(如图11)则在上必然存在点P′使得∠OAP更大,故仅当直线AP与⊙O相切时,∠OAP最大,此时Rt∆AOP′中,sin ∠OAP=,所以∠OAP的最大值为30◦.

图11

论证起来,考虑∠OAP的邻边OA为定长,可以作OB⊥AP于点B(如图12),考察Rt∆AOB中,sinA=(仅当B与P重合时取等),所以∠OAP≤30◦.

图12

此时问题可一般化为:半径为r的⊙O外有一点A,OA=d(d >r),P为⊙O上一点,则∠OAP的最大值为.

其二,定点在圆内.如图13,点A在半径为3的⊙O内,点P在⊙O上,当∠OPA最大时,S∆AOP=____.

图13

同上,考虑∠OPA的邻边OP为定长,可以作OB⊥AP于点B(如图14),考察Rt∆POB中,仅当B与A重合时取等,此时OA⊥AP(如图15),AP=此时.

图14

图15

此中的角度最大值问题,亦可一般化为:半径为r的⊙O内有一点A,OA=d(d