巧设题·重联想·散思维——一道中考复习题的解法探究

江苏省南京市金陵中学仙林分校中学部(210000)孔伟伟

1 原题呈现

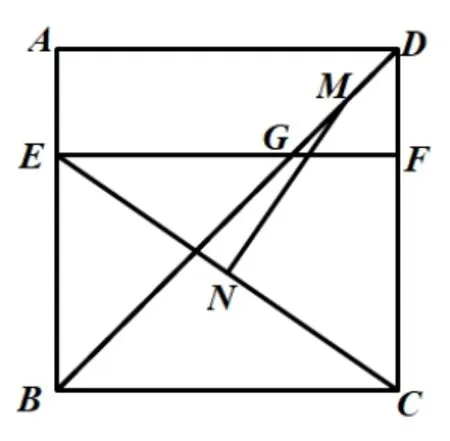
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF//BC,分别交BD、CD于点G、F两点,若M、N分别是DG、CE的中点,求MN的长.

2 试题评价

此题为2017年浙江宁波市第10 题,本题虽以选择的形式考察,但方法多样,题目中蕴含正方形、矩形的多个性质,考察中位线定理、直角三角形斜边中线定理、等腰三角形三线合一、勾股定理等知识点,因此可以从不同的角度分析和挖掘题目.同时需要学生借助基本模型灵活运用知识,对学生思维水平要求较高,同时进行细致的观察、合理的联想、严谨的推理,能够较好地考察学生数学抽象、逻辑推理、数学建模、数学运算等素养.

3 解法探究

3.1 利用三角形中位线

解法1:看如图1所示,取DF、CF的中点H、K,连接MH、NK;∵MH、NK分别为∆DGF和∆CEF的中位线,易证四边形HMRK为矩形,∴MR=HK=HF+FK=3,∵∆DMH为等腰直角三角形,∴MH=DH=1,RK=1,NR=2,∴在Rt∆MRN中,.

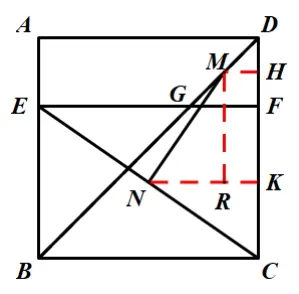
图1

解法2:如图2,连接FM并延长交AD于点Q,连接QG、BQ、BF,∵四边形BECF为矩形,且N为CE中点,∴BN=NF,易证四边形DQGF为正方形,∴MN是∆BFQ的中位线,.

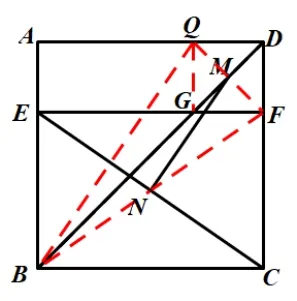
图2

解法3:如图3,延长GN交BC于点H,易证∆EGN∽=∆CHN,∴N为GH的中点,∴MN为∆GHD的中位线;∵∆DFG为等腰直角三角形,DF=FG=2,.

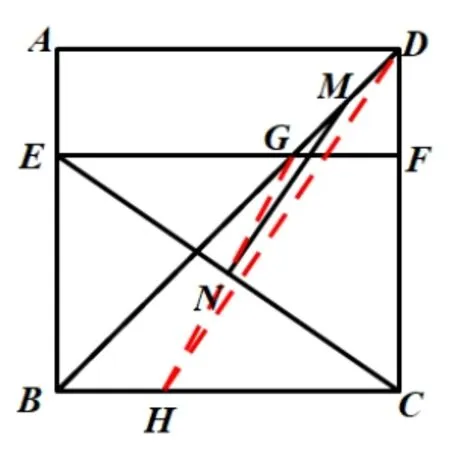
图3

3.2 利用等腰三角形三线合一

解法4:如图4,连接CM、EM,取DF中点P,连接MP,延长PM交AB于点H;由正方形的对称性易证∆HEM∽=∆PMC,∴MC=ME,∵∠EMC=90◦,.

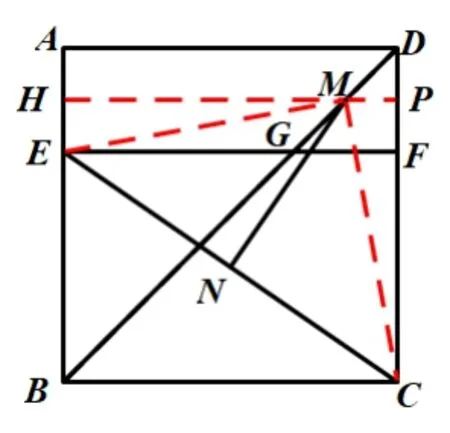
图4

3.3 利用直角三角形性质:“斜边中线等于斜边一半”

解法5:如图5,连接MF,BF,∵四边形BECF为矩形,且N为CE中点,∴BN=NF,易证∆DFG为等腰直角三角形,∵M为DG中点,∴FM⊥DG,在Rt∆BFM中,.

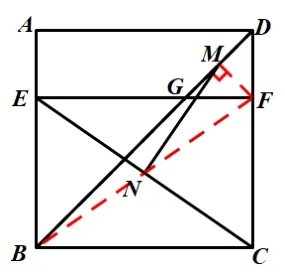
图5

3.4 利用平面直角坐标系

解法6:如图6,建立如下平面直角坐标系,由题可知设:C(6,0),E(0,4),D(6,6),G(4,4),由中点坐标公式可得:.

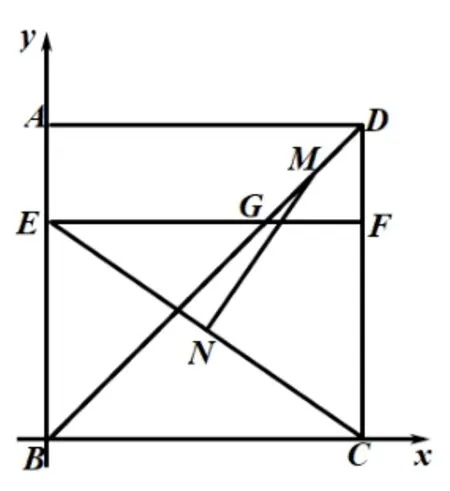
图6

3.5 利用梯形中位线

解法7:如图,取AE的中点K,BE的中点H,连接MK、NH,作NJ⊥KM,∵MK为梯形AEGD的中位线,∴5,∵N、H分别是BE、CE的中点,易证四边形KJNH为正方形,∴KJ=HN=NJ=3,.

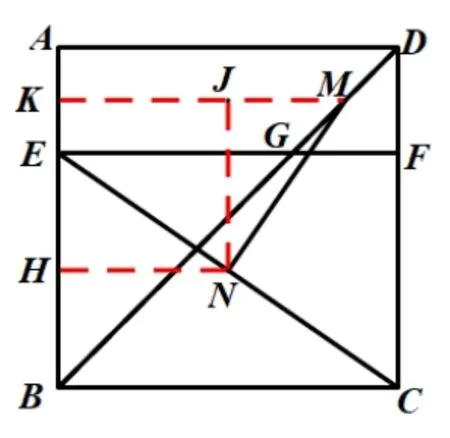
图7

4 解后反思

4.1 体验联想,唤醒自我认知

解题教学,教师应该尽可能引导将数学知识按照一定的逻辑进行联结,避免“碎片化”学习,注重开发学生联想思维,从“想不到”到“能想到”,甚至想到更多的“巧法”.此题中的关键元素是中点,看到中点首先可以想到三角形中位线定理;看到等腰和中点,想到等腰三角形三线合一;看到特殊四边形对角线中点,想到连接另一条对角线;看到直角三角形和斜边中点,想到“直角三角形斜边中线等于斜边一半”;看到平行和中点,想到倍长中线构造全等;在平面直角坐标系中,看到中点想到中点坐标公式,化形为数.数学中很多复杂的问题都是由熟悉的、基本的几何模型演变而来,引导学生产生联想,有助于唤醒学生已有的认知,对问题产生新的想法,找到解题思路.

本题中的条件“四边形ABCD是边长为6 的正方形”若变成“四边形ABCD为矩形,AB=6,∠ABD=60◦”,仍然可以求出MN的长度;当然条件可以更一般化为:四边形ABCD为平行四边形,AB=a,BC=b,∠BAD=α,∠ABD=β,AE=c,如图8所示,通过解三角形和三角形中位线定理即可得MN的长.解题教学不是简单的解决一道题,更多地关注重要结论性质的拓展与推广.在变式教学中,学生可以从多角度、多层面、多结论去认识,从“变”的现象中发现“不变”的本质,有效提高学生的学习效率和探索能力,提升思维层次,发展学生的数学学科素养.

图8

4.2 分析问题,拓展思维深度

波利亚说:掌握数学就意味着善于解题.教师在解题教学中,既要分析题目中的显性和隐性的条件,也要分析题目条件与结论得内在逻辑结构,深度挖掘题目中的基本几何模型、蕴含的数学方法和数学的本质,从而培养学生思维的发散性、条理性和融合性.本题充分利用中点这个元素,通过对中点的联想,从不同的切入点思考,帮助学生巩固所学知识,提高知识应用能力,实现深度学习.