扇形面积公式与三角形面积公式的内在联系

上海市宝山区上海新闻出版职业技术学校(200431)有四普

1 引言

初中阶段学生已经学习了扇形面积公式和弧长公式,在高中阶段学习弧度制的时候,又学习了在弧度制下的扇形面积公式.然而就是在这一新的公式形式的学习过程中,学生发现扇形的面积公式和弧长公式识记比较困难,公式的规律性不太明显.出现这种情况的原因有三:一是由于初中阶段教材内容安排以及教师指导学生学习过程中使用了传统的教学过程;二是高中阶段教师未对公式进行深层次的处理和解释,学生未能完全理解扇形面积公式的实质;再者还有部分学生处于“尽信书”的状态,不对公式的来龙去脉进行一番思考和求证.

2 初中阶段的教学过程

“弧长和扇形面积”的教材编写过程和一般的教学过程大致经历这样几个阶段:问题情境→思考并得出公式→用公式解决问题情境中的问题→公式的再应用[1-2].传统的教学过程也会让学生经历从特殊到一般的过程,从而来推导出扇形的面积公式,培养学生的探究意识和归纳能力.在经历这一过程后学生也基本能够做到识记和推导扇形面积公式,但是作为教育来说,这是远远不够的.

在传统的推导扇形面积公式的过程中,教师一般会创设情境让学生经历从特殊到一般的过程,从而来推导出扇形面积公式.这个过程一般是这样的:给出一个半径为R的圆和一组半径都为r扇形,这些扇形的圆心角分别是270◦,180◦,90◦,60◦,30◦,1◦,n◦(此处仅为举例,与教学过程采用数据并非严格一致),如下表1所示:

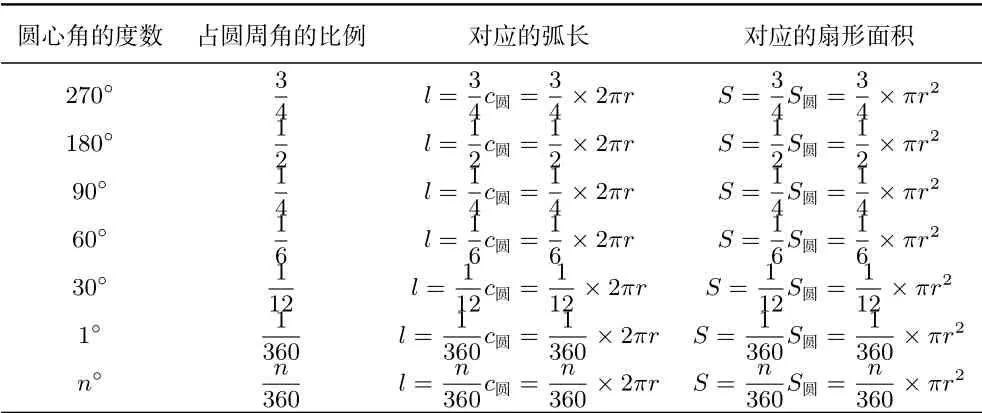
表1 扇形面积变化与圆心角度数变化之间的规律

在这里采用的是部分与整体,由特殊到一般的归纳方法,从而推导出扇形面积公式[3].学生们在初中学习的时候大致就是经历的这样一个过程,老师们也基本上采用的是这一教学设计思路,出现这样的情况主要和我们学生初中阶段的学情和教材安排有关.

3 高中阶段的教学过程

高中阶段的扇形面积公式是在学习弧度制时提出来的,在这一学习阶段,学生学习了弧度制,弧度制下的弧长公式:

在这里l表示弧长,α表示弧所对应的圆心角的弧度数,r表示扇形所在圆的半径,根据任意角的角度制与弧度制之间的转换关系:

初中给出的角度制下扇形面积公式为:

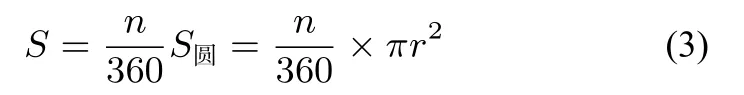
将公式(1),(2)代入(3)即得弧度制下的扇形面积:

高中阶段的弧度制下的扇形面积公式也就这样给出了,这样给出的公式(4)使学生感觉像是一种推导式,不便于学生们的理解与识记.于是在学生们对新的公式的记忆变得模糊时,又得从初中所学的公式里面推导出来,且不说这里面无法保证所有的学生都能完成推导,更有一个重要原因是无法让学生去真正理解知识、领悟知识、收获知识从而实现自我的发展,这也不是我们愿意看到的教育[4-5].

也正是因为学生们在初中学习的时候采用的学习方法再加上高中阶段给出的弧度制下的扇形面积公式的导出式,从而导致学生在后面的学习过程中对扇形面积公式产生了困惑与识记困难.

4 三角形面积公式与扇形面积公式的内在统一性

笔者在设计和教授本节课时采用了支架式教学法[6],前面的教学过程和传统的教学过程也比较类似,但是在导出公式(4)之后笔者会让学生们观察公式(4),并且在这里设置了一个探索环节:a.公式(4)和我们以往学习的什么公式比较类似;b.出现这一现象是巧合吗,请分析原因.

学生们在观察之后发现公式(4)与三角形的面积公式在形式上高度相似,几乎可以认为是一样的,但是对于问题b的回答却始终得不到一个圆满的结果,有的同学认为此时可以把扇形认为是一个三角形,但是就是说不出具体的原因.

笔者为了让学生们清楚知道出现这一现象的原因,给同学们渗透了极限的思维,让同学们观察下图1:

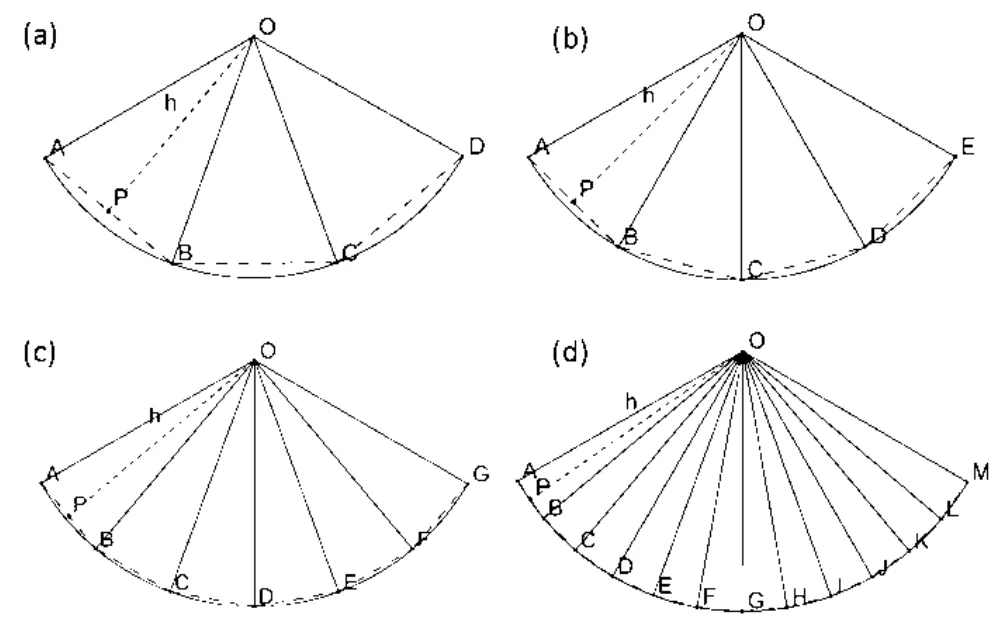
图1

为什么会出现这种情况呢?笔者在教学的过程中前半部分也采用了上文中高中阶段学习的框架,只不过笔者在此基础上进行了内容的拓展,让同学们观察上图的变化,体会三角形与扇形之间的形态变化.

观察发现,我们把一个扇形分割成若干个全等三角形时,随着分割次数的增加,分割出来的小扇形越来越近似三角形,它的面积也越来越接近于小三角形的面积,当分割次数n趋近于无穷大时必然有扇形的面积等于三角形的面积,即:

当n趋近于无穷大时,三角形的高h∆AOB与扇形的半径r相等,三角形的底边AB的长等于小扇形的弧长lAB,nlAB就等于大扇形的弧长l,于是有:

从公式(6)中可以发现,求解扇形的面积是通过求三角形的面积来实现的,也就是说扇形的面积出自于三角形的面积.

因为扇形可以看成是无数个全等的底边无限小的等腰三角形组成的,因此扇形的面积才会与三角形的面积出奇的相似,也就是说扇形的面积公式与三角形的面积公式具有内在统一性.如果我们把扇形的弧看成是“底”,半径看成“高”的话,则扇形就可以看成一个特殊的三角形了,其面积公式和三角形的面积公式那就是一样的了,这也就很好地解释了为什么扇形的面积公式会与三角形的面积公式很相似.

经过上述解释,学生对扇形的理解更加深刻.同样的方法也可以应用到弧长公式上,学生们对于扇形的面积公式以及弧长公式的认识也更加深刻,也解决了学生在学习扇形时遇到的公式识记困难以及对公式形式的困惑,并且在探讨的过程中有效拓宽了学生的数学思维,促进了学生对极限思想的理解.

5 结论

扇形的面积公式与三角形的面积公式具有内在统一性,可以用一个统一的形式表示出来.数学中有许多图形的面积公式可以用一个统一的形式表示出来[7],因此在教学过程中我们需要把公式的来龙去脉弄清楚[8],看清各个公式之间的内在联系,这样既有利于提升我们课堂的效果,同时也有助于实现对学生的真正教育,促进学生的发展.