全站仪悬高测量功能应用研究

邵禹铮 SHAO Yu-zheng

（中铁十二局集团国际工程有限公司，天津300308）

0 引言

当今先进科技的飞速发展，随之测绘仪器也不断更新，全站仪是工程测量中被常用的高精度仪器，并且向半智能、全（半）自动化的方向发展。为了更好的发挥全站仪的测量功能，熟悉全站仪的内部的测量程序功能是必不可少的，如悬高测量、后方交会、对边测量、面积测量的程序功能。针对于悬空的构筑物或线路（如高耸的烟囱或高压线等），当测量规范精确要求测量其悬高时，鉴于不能够（或不方便）在悬高物体的天底点处安置反光棱镜，尽管具有免棱镜测量功能的全站仪，同样具有条件满足不了情况。这时候一般利用全站仪的其他程序进行间接测量的方法，通过间接测量方法测得悬高。传统的方法，首先要准确的找到悬空点的垂线与地面点的交点，人为的在投影点处立反射棱镜，按测距键测出竖直角与斜距，之后利用数学函数关系计算出目标点的高度，悬高测量时使用全站仪不常用的测量程序功能。可易测出架空物体的悬高，但是要精确的找到架空目标在地面的铅垂投影点的点位并不容易。对传统单向悬高测量的方法和计算公式进行改进，可测出较为准确架空物体的悬高。

1 全站仪悬高测量功能

1.1 悬高测量基本原理与方法

悬高测量是指测量悬空中的某点（如高压线、烟塔等）垂直于某平面（一般指地面为多）的高度。全站仪进行悬高测量，首先把全站仪安置在到建筑物距离约为目标高度的3倍。假设测站点为O，悬空点为A，全站仪对中整平安置好后，把反射棱镜立在欲测悬空点A与地面的垂足点A′、上（即过欲测点A的铅垂线与地面的交点），然后读取此时的棱镜高V记录下来，并将棱镜高值输入全站仪中，在用全站仪的望远镜照准反射棱镜，按下测距键，把水平制动，竖直转动望远镜直至照准要测量的目标点A，这时全站仪屏幕上显示的数值就是悬空点至地面的高度H，其计算公式：

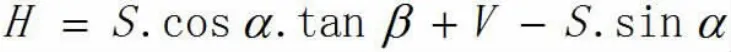
其原理图如图1。

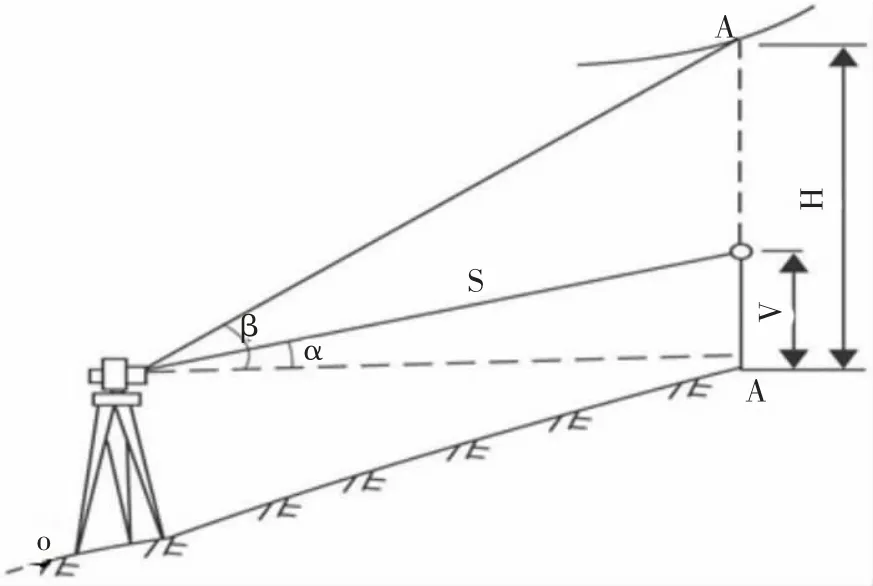
图1 悬高测量的原理

1.2 精度分析

根据误差传播定律，可得上式的误差公式为：

①对测角α求中误差：

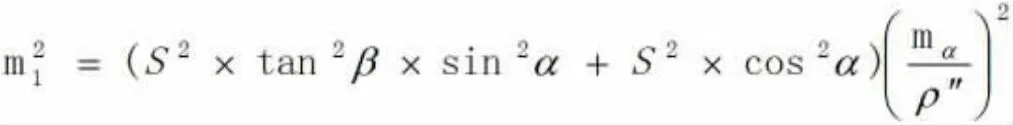
②对测角β求中误差：

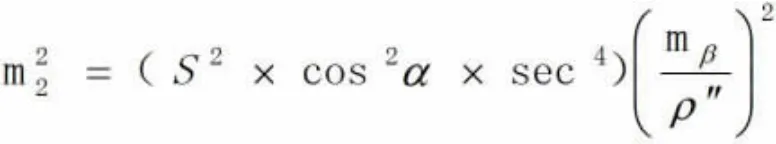
③对斜距S求中误差：

对镜高V求中误差：

则悬高的中误差为：mH2=m12+m22+m32+m42，令mα=mβ=m仪器，则：

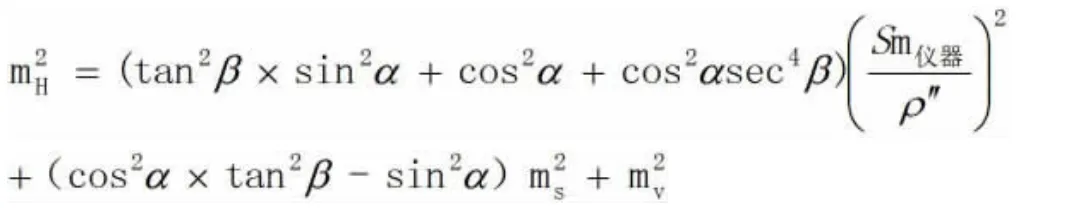
有上式分析可知，我们可以有目的性的根据测站点的位置控制仪器至棱镜的竖直角α，令α为零，因此有：

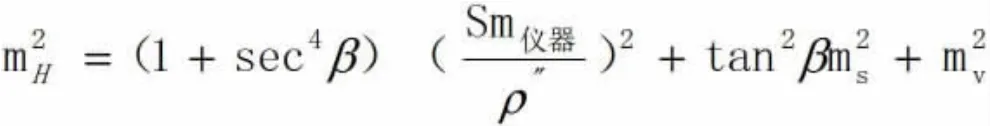
由此公式可以看出影响悬高测量的主要误差是仪器至待测点的竖直角β，全站仪半测回的测角误差，全站仪至棱镜的斜距S，全站仪的测距误差，棱镜高的读取误差。在实际测量中，测角和测距误差是属于仪器本身的误差，不可避免的误差，我们实际能控制的是仪器至棱镜的斜距以及仪器至目标点的竖直角。现令：

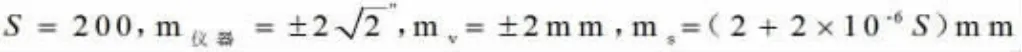
得出表1。

表1 数据分析

由表中的数据分析可知，当全站仪与待测点的竖直角β≤45°时，其求得的中误差较小，能满足工程测量的需求，因此，当我们在野外应用全站仪进行悬高测量时可以控制竖直角来减小误差的出现。

1.3 悬高测量存在的不足之处

由上面推导可知，其原理比较简单，实际操作也是很便捷，在工程施工测量中我们利用该项特殊的程序功能，就能快速的测定出高压线、悬空物体的高度。但是在一些高精度的测量工作中，由于要求的精度较高，这时就需要我们将反射棱镜准确无误的安置在被测目标点与地面的垂足点上，在实际的野外测量中，这些垂足点A′不能准确的找到或者有些垂足点就不能放置棱镜，如垂足点在河道、深谷或待测点为塔的塔尖，这时传统的悬高测量就不能使用。

2 单向观测法的原理与方法

首先在距离目标点到地面点高度的3倍处A点安置全站仪，量取全站仪的仪器高iA，对中整平后，照准目标点D，测得竖直角为α，将全站仪的水平制动，调节竖直制动螺旋，在与目标点与测站点同一铅垂面内合适的位置选定一个地面点B，以及水涯线上一点C，在A点按距离键测得A、B间的斜距SAB。然后在B点安置全站仪，在A点置反射棱镜，此时为了计算的方便令棱镜高竖直角β，倒转全站仪的望远镜照准目标点D，测得竖直角γ1，在照准棱镜点C，棱镜高VA等于iA，之后先照准后视点A，测量出为VC，测得竖直角为γ2，在测得B、C间的斜距SBC。

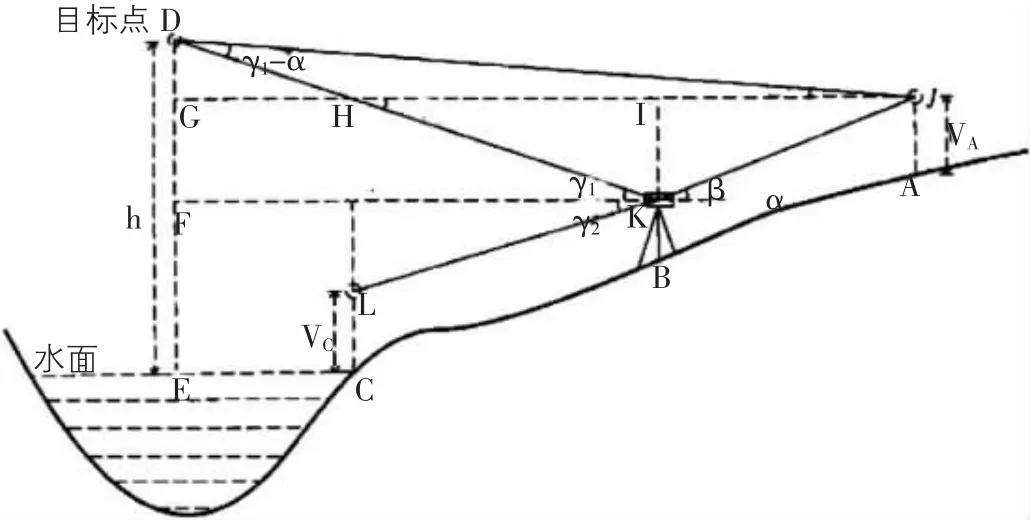
图2 单向观测法原理

故悬高为：

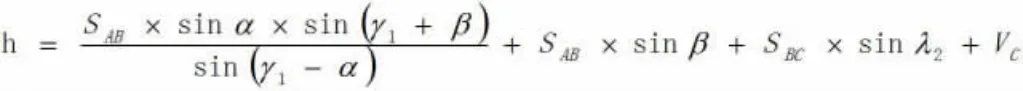
单向观测法存在的问题，操作比较繁琐，此过程需要立三次反射棱镜，设两次站，因而会存在系统误差，过程越繁琐传播的误差就越大。还需保证A、B、C点以及目标点D在同一铅垂面内。在实际操作过程中很难保证四点在同一铅垂面内。此法的计算公式较复杂，需要的测量的已知数据较多，还需应用多个三角形，每个测得的数据都会带有误差，多个带有误差的数据最终汇集在一起，代入公式，最后计算的结果产生的误差越大。

3 单向观测法的原理的改进方法

3.1 设计方案

将全站仪置于距目标点至底高度的约1.5倍处，标记后对中整平；瞄准目标点，读竖直角记录并量仪高；全站仪的水平制动，倒转望远镜，下俯望远镜视准轴，在同一铅垂面内选定一个适合的A点，在A点设站对中整平；在水洼岸边的合适位置选一个点D，保证所选的点与水静止的平面在同一个水平面上，在该点上立反射棱镜，此时的镜高，全站仪照准反射棱镜，得A、D间的斜距及竖直角；全站仪瞄准目标点C，记录竖直角。在B点立反射棱镜，镜高为前次仪器高，得A、B之间的斜距及竖直角。改进公式推导及原理如图3所示。

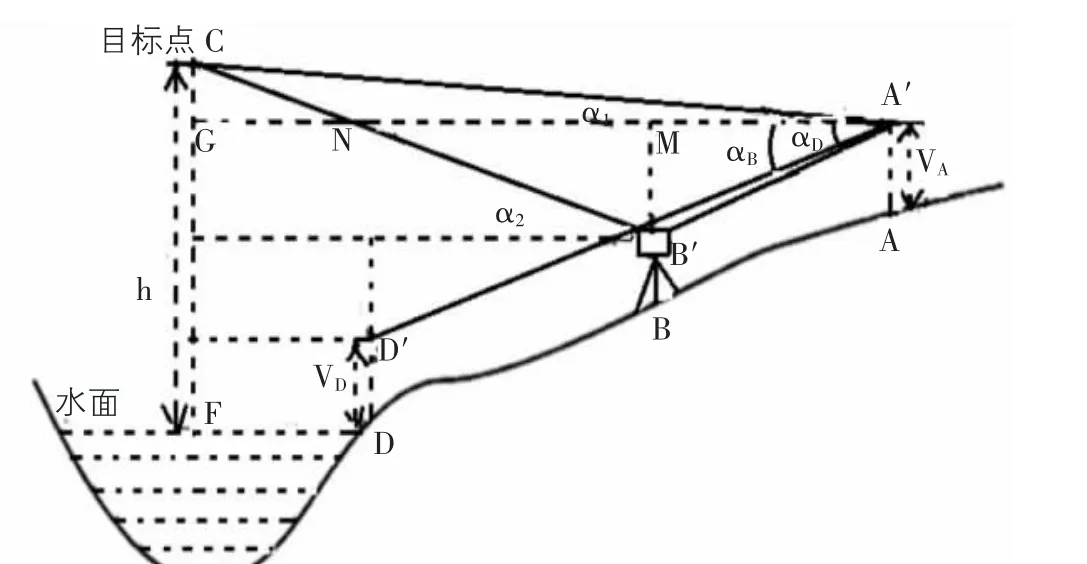
图3 改进单向观测法后的原理

故所求的悬高为：

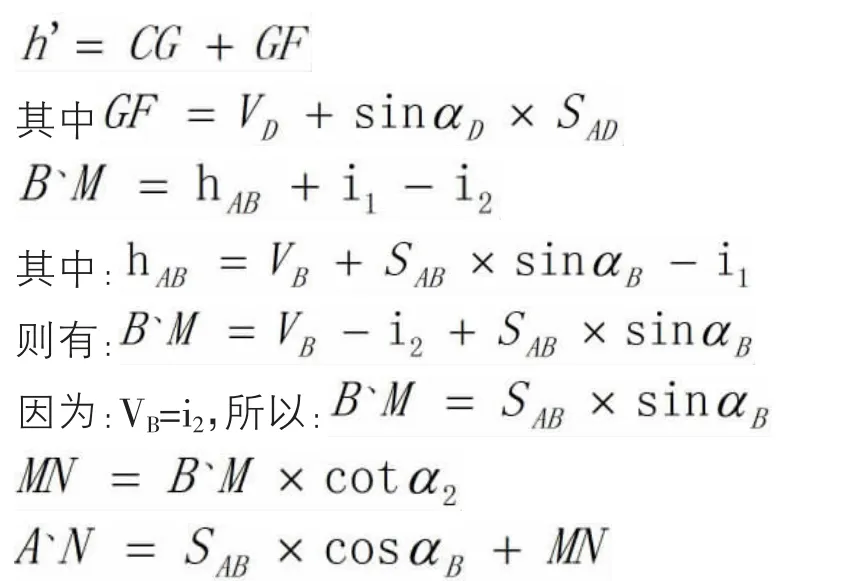
逐次代入最后求得的悬高为：

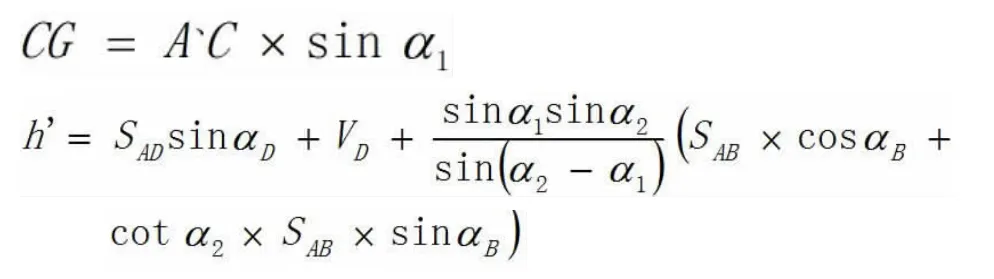
3.2 对改进后悬高测量进行精度分析

根据误差传播定律对悬高H，即，求中误差：

①对SAD求中误差：m12=sin2αDmS2

②对斜距SAB求中误差：

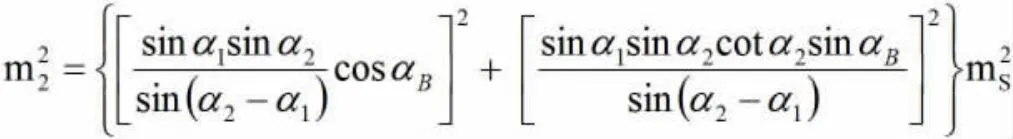
③对VD求中误差：m32=mD2

④对竖直角α1求中误差：

⑤对竖直角α2求中误差：

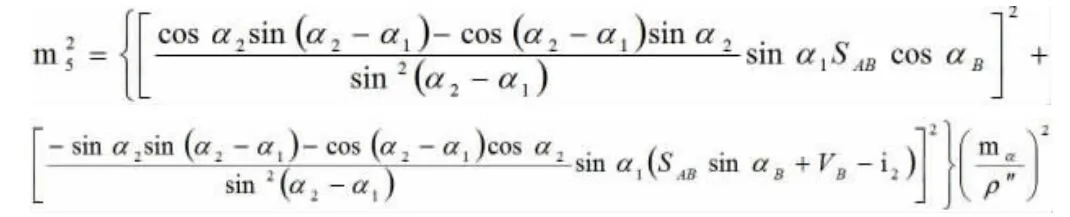
⑥对竖直角αB求中误差：

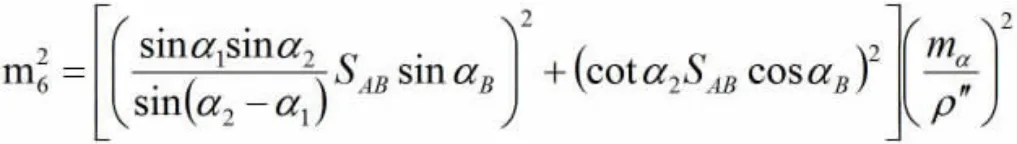
⑦对竖直角αD求中误差：

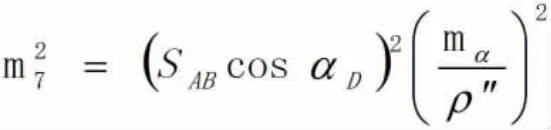
则悬高的中误差为：

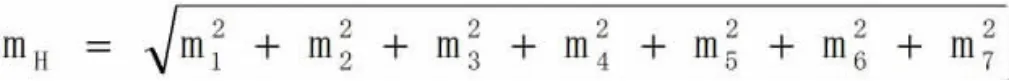
其中令：

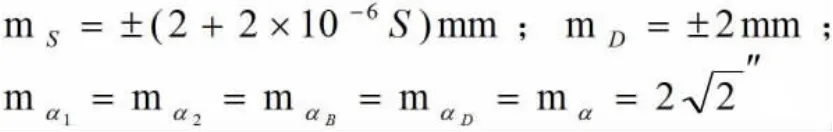
4 实际应用

4.1 数据采集以及数据处理分析

4.1.1 第一组测量数据

传统单向观测法测量三次路灯的高度分别为12.699米、12.695米、12.697米，三次取平均值的路灯高H=12.697米。

间接法测得的数据为：α1=9°28’28”；α1=19°21’43”；VB=i1=1.532；VD=1.9

D：αD=1°33’07”，SD=48.535，HD=48.510；B：αB=1°20’52”，SD=27.212，HD=27.203

最后用这个公式间接求得悬高和精度：h’=12.690；ΔX=|h’-H|=0.007

由误差传播定律得悬高的中误差：mH=0.049，由ΔX=0.007＜0.049，得此方法满足工程。

4.1.2 第二组测量数据

传统单向观测法测量建筑物的高度分别为41.86米、41.84米、41.87米，三次取平均值的建筑物高H=41.856米。

间接法测得的数据为：α1=14°19’37”；α1=17°25’07”；VB=i1=1.468；VD=1.6

D：αD=-1°1’24”，SD=162.317；B：αB=-0°25’58”，SD=22.724，

最后用这个公式间接求得悬高和精度：h’=41.87；ΔX=|h’-H|=0.013

由误差传播定律得悬高的中误差：mH=0.05，由ΔX=0.013＜0.05，得此方法满足工程。

通过两组数据充分验证了该方法能在保证精度的条件下更好地进行操作，能很好地在工程实际中应用。

4.2 程序的编写

上述算法计算过程通过C++编程实现，代码如下：

5 结束语

在工程施工测量中利用该悬高测量程序功能，就能快速的测定出高压线、悬空物体的高度。在一些高精度的测量工作中，这时就需要我们将反射棱镜准确无误的安置在被测目标点与地面的垂足点上，但是在实际的野外测量中，这些垂足点不能准确的找到或者有些垂足点就无法到达（如垂足点在河道、深谷或待测点为电视塔的塔尖），这时传统的悬高测量就不能使用。对间接的悬高测量的单向观测方法存在的不足进行改进，得到更适合操作的悬高测量方法，其方法实用性强，可以使普通型全站仪的功能得到更全面的发挥。