经管类微积分中一阶微分方程的教学设计

◇上海立信会计金融学院统计与数学学院 杨 瑜 魏贺杰

本文将经典的SIR模型引入到经管类微积分的一阶微分方程的教学内容中，并给出Matlab程序，对培养学生的好奇心和提高编程的能力有良好的效果。

1 引言

2020年9月11日习近平总书记在科学家座谈会的讲话中指出要把教育摆在更加重要位置，全面提高教育质量，注重培养学生创新意识和创新能力。笔者所在的学校是一所会计、金融特色鲜明的公办全日制普通高等学校。每学年很多专业的学生要主修经管类的微积分课程，采用的教材是吴传生教授编写的《经济数学-微积分(第三版)》。注意到教材中第十章第二节有关一阶微分方程的平衡解及其稳定性的内容偏少而且不涉及编程方面的教学内容。2018年4月，教育部印发了《教育信息化2.0行动计划》将信息技术纳入初、高中学业水平考试。如何将高中数学与大学的微积分课程进行较好的衔接以及更好的培养学生的好奇心？这是一个非常值得去思考的问题。根据笔者多年的教学经验，将自身的专业知识以及Matlab编程融入到教学中，这样能更好的激发学生的学习兴趣。本文将以SIR模型为教学切入点，介绍一阶微分方程的相关概念并给出相应的Matlab程序。

2 教学案例设计

2020年9月8日在全国抗击新冠肺炎疫情表彰大会上习近平总书记指出新冠肺炎疫情是百年来全球发生的最严重的传染病大流行。为了让学生理解传染病的传播规律以及如何科学的采取措施进行预防和控制，本文将经典的SIR模型融入到一阶微分方程的教学中。

2.1 案例引入

传染病动力学中经典的SIR模型[1]如下：

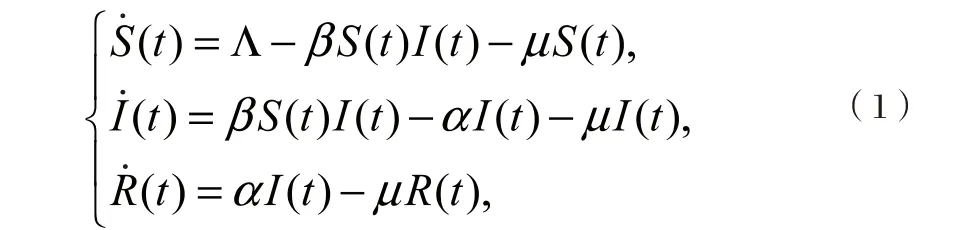
关于模型（1），我们重点考虑以下三个问题：(i) 它的平衡点有几个？(ii) 它们的稳定性如何；(iii) 基本再生数与哪些参数有关。

2.2 案例分析

根据实际的意义，只在第一卦限对模型（1）进行讨论。模型（1）的平衡点满足

如下的代数方程组：

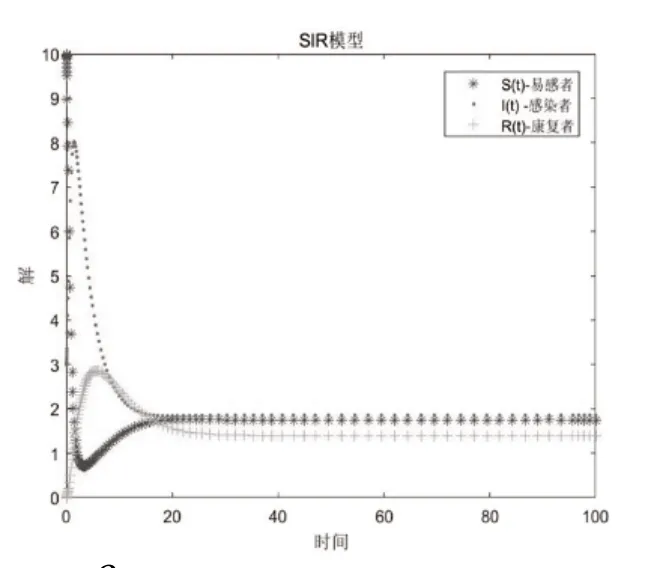
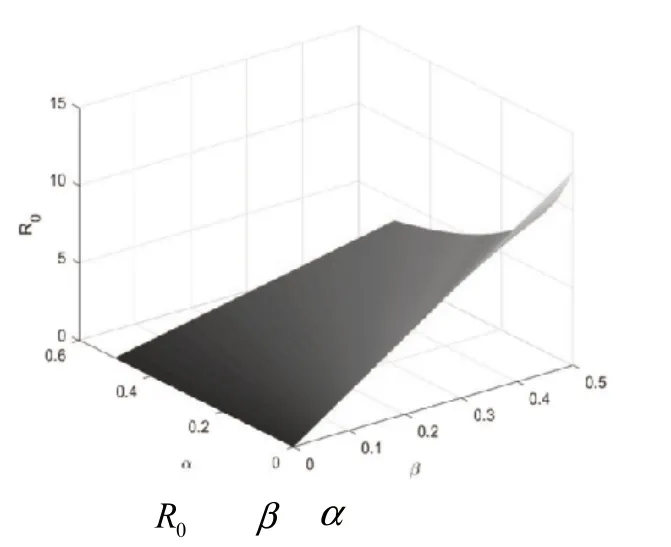
微分方程可用来描述物质的运动，而稳定性有明显的物理意义。如果描述质点运动的微分方程的特解是不稳定的，那么初值的微小干扰将导致“差之毫厘，谬以千里”[7]。由文献5知，当时，模型（1）只有无病平衡点且是全局渐近稳定的；当时，无病平衡点是不稳定的，而唯一的地方病平衡点是全局渐近稳定的。由基本再生数的表达式知，接触率的减少或者感染者恢复率的增加将使其值减小。故传染病暴发时，人们可以采取居家隔离、出门时佩戴口罩、注意个人卫生习惯及提高公共的卫生设施和医疗水平等措施切断传染病的传播途径，从而使传染病更好的得到控制，缓解大众的恐慌和焦虑情绪。

2.3 Matlab程序

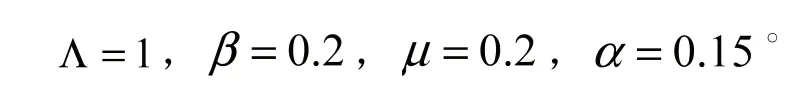
选取如下参数[8]：可得，故（1）的无病平衡点是不稳定的，唯一的地方病平衡点是全局渐近稳定的。

地方病平衡点稳定性的Matlab代码如下：

2.4 知识延伸

现实生活中有些传染病的发病具有明显的季节性，如流感和登革热；有些传染病只针对某个年龄段的人群，如手足口病。因此，在建模过程中须考虑如周期、年龄和时滞等因素的影响。故原来的常微分方程就要变为相应的周期微分方程、年龄结构方程和时滞微分方程等来刻画传染病的传播规律。

3 结束语

本文将专业知识融入到一阶微分方程的教学内容中，培养了学生的创新思维和意识，提高了应用数学理论解决实际问题的能力。作为专业教师如何将专业的前沿知识更好的融入到教学中，我们的工作任重而道远。