基于时间序列分析法的种群动态变化研究

高继文

(合肥财经职业学院 现代服务业学院,安徽 合肥 230601)

0 引言

种群动态变化是生态学研究的重点,通过对种群数量的预测可以更好地了解群落结构的稳定性,科学把握生态系统的变化规律。例如,近年普林顿珠研究了藏羚羊种群数量动态变化问题,指出藏羚羊种群数量呈现出先减少后增加的趋势,其在时间尺度和空间格局上具有显著差异,且人为因素是影响藏羚羊种群数量的主要因素[1]。李维根研究了辽宁省榛黄达瘿蚊种群数量动态变化问题,指出瘿蚊种群数量先增加后下降,前期种群数量呈稀疏泊松分布,后期呈不均匀核心分布[2]。张真研究了马尾松毛虫种群动态变化问题,采用时间序列的自相关函数来分析马尾松毛虫的时间动态,指出马尾松毛虫种群数量的变化是平稳的,但周期性不显著,种群数量动态变化不存在混沌现象[3]。时间序列分析法是通过对序列历史的分析来把握序列变化规律,包括自回归模型、移动平均模型、自回归移动平均模型、求和自回归移动平均模型、季节模型等,在经济学、社会学、生态学等许多领域具有十分广泛的应用[4]。本文采用时间序列分析法对捕食者和猎物两类种群动态变化进行研究,期待对更好地把握捕食者种群和猎物种群动态变化规律提供参考。

1 时间序列分析模型

1.1 ARMA模型

自回归滑动平均模型(auto regressive moving average mode,ARMA)是对平稳随机过程分析的典型方法[5]。伴随着时间的推移,种群数量也将产生变化,种群数量形成一个随机序列,预测种群数量的随机序列和原始种群数量在时间上存在连续性。种群数量序列的变化受到两个方面的影响,即影响因素和自身变化规律。设x1,x2,…,xp为影响因素,根据回归分析可得:

yt=β1x1+β2x2+…+βpxp+Z

(1)

式中:yt为预测对象观测值;βi,i=1,2,…,p为回归系数;Z为误差。

预测对象观测值yt受自身变化规律的影响,即

yt=β1yt-1+β2yt-2+…+βpyt-p+Zt

(2)

对于种群的变化,误差项在种群变化的不同阶段具有不同的依存关系,即

Zt=εt+α1εt-1+α2εt-2+…+αqεt-q

(3)

因此,ARMA模型的表达式可以表示为:

yt=β1yt-1+β2yt-2+…+βpyt-p+εt+α1εt-1+α2εt-2+…+αqεt-q

(4)

式中:β为自回归系数;α为滑动平滑系数;p为自回归滞后阶数;q为滑动平均滞后阶数;ε为白噪声序列。

从ARMA模型的建模过程可知,采用ARMA模型对种群动态变化进行预测,不仅考虑了种群数量对时间序列的依赖,同时也考虑了随机波动的干扰,能够有效地对种群短期的动态变化进行高精度的预测。

1.2 NLAR模型

非线性自回归模型(nonlinear auto regressive,NLAR)是对非平稳随机过程分析的典型方法[6]。设函数φ为Rp到R1的可测函数,{εt}均值为0,标准差σ为白噪声序列,那么随机序列{xt}可以表示为:

xt=φ(xt-1,…,xt-p)+εt

(5)

式中:p为模型阶数。

NLAR模型阶数p的确定往往采用AIC准则,该准则是衡量统计模型拟合优劣性的重要标准,其建立在熵概念基础之上,可以有效地权衡模型的复杂度。AIC的计算公式为:

AIC=2k-2Ln(L)

(6)

式中:k为参数数量;L为似然函数。

1.3 GM(1,1)模型

GM(1,1)模型是通过对时间序列累加生成趋势明显的序列,通过对趋势明显的序列建立预测模型,同时通过累减的方式获得原始数据序列,进而实现预测的灰色模型。GM(1,1)模型对种群数量动态变化预测的流程如图1所示[7]。

图1 GM(1,1)预测模型流程

不妨设原始数据为x(0)=(x(0)(1),x(0)(2),…,x(0)(n)).考虑到种群数量原始数据存在比较大的随机波动性,对原始数据进行累加得到新的序列x(1),即

(7)

由新序列x(1)按照等权方式来构造邻均值等权序列z(1),即

z(1)=(z(1)(2),z(1)(3),…,z(1)(n))

z(1)(k)=0.5x(1)(k-1)+0.5x(1)(k)

(8)

由灰色理论建立序列x(1)的一阶一元微分方程,即

(9)

式中:a为发展系数;u为灰色作用量。

(10)

其中,

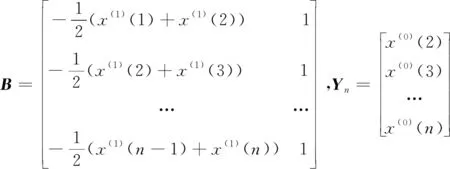
(11)

(12)

将预测结果进行累减还原,便可以得到种群动态变化预测值。

2 实例分析

2.1 数据来源

自然界包含捕食者和猎物种群,捕食者和猎物之间处于相对平衡的状态,从而维持整个生态环境的平衡。本文的数据为一个双变量的时间序列,即捕食者种群数量时间序列和猎物种群数量时间序列。对捕食者和猎物种群数量每年收集10次,共收集20 a的数据。图2给出了捕食者种群数量和猎物种群数量变化情况。

图2 种群数量动态变化情况

由图2可知,猎物数量减少导致捕食者种群数量出现拥挤,最终使得捕食者种群的数量减少。本文选择捕食者种群数量和猎物种群数量的前半部分作为进行模型参数估计的数据,从而求得捕食者和猎物种群数量变化的预测模型。采用剩余的后半部分数据来验证所建立预测模型的精度。

2.2 结果分析

捕食者-猎物模型是简单且具有使用价值的例子,通过对捕食者以及猎物种群数量建立预测模型,可以更好地了解种群的变化情况。捕食者和猎物之间是一种相互依存的关系,伴随着捕食者数量的下降,猎物的数量就会上升,一旦超过了极限值,就会破坏生态平衡;伴随着捕食者数量的增加,猎物的数量就会下降,一旦低于极限值,捕食者的数量也会因为没有食物而下降,导致生态平衡的破坏。分别采用ARMA模型、NLAR模型以及GM(1,1)模型对捕食者种群以及猎物种群数量的变化进行动态预测,捕食者种群动态变化预测结果如图3所示,猎物种群动态变化预测结果如图4所示。

图3 捕食者种群动态预测

图4 猎物种群动态预测

由图3可知,采用GM(1,1)模型对捕食者种群动态预测的结果精度最高,采用ARMA模型对捕食者种群动态预测的结果精度最低,采用NLAR模型对捕食者种群动态预测的结果精度居中。

由图4可知,三种预测模型对猎物种群动态预测的结果表明:依旧是GM(1,1)模型精度最高,ARMA模型最差,NLAR模型居中。捕食者以及猎物种群数量的动态变化是非平稳随机过程,而ARMA模型对平稳随机过程的预测精度较高,在处理非平稳过程时性能比差。NLAR是典型的非平稳随机过程处理方法,在对捕食者以及猎物种群动态变化预测方面的性能优于ARMA模型。GM(1,1)通过累加消除了捕食者以及猎物种群动态变化的随机波动性,对种群动态预测的精度更高。

3 结论

种群动态变化是典型的时间序列,通过时间序列分析法对种群动态变化进行预测,能更好地确保群落结构的稳定性,维持生态平衡。本文建立了ARMA、NLAR以及GM(1,1)预测模型,并将其应用于实际的捕食者和猎物种群动态变化预测中。预测结果表明,GM(1,1)模型的预测精度最高,ARMA模型的预测精度最差,这对种群数量动态变化的预测具有一定的参考价值。