气固流化床中介尺度流动结构研究进展

牛 犁，刘梦溪，王海北，刘贺磊

(1.矿冶科技集团有限公司 冶金研究设计所，北京 100160；2.中国石油大学(北京) 化学工程与环境学院，北京 102249；3.北京理工大学 化学与化工学院，北京 100081)

0 引言

气固流化床反应器是一种在石油化工行业中被广泛应用的反应器，具有结构简单、流化颗粒尺寸分布范围广、传质和传热效率高等优点，同时也普遍存在相间接触效率低下、传递受限或传递与反应不匹配等问题。流化床内气体与固体颗粒间的流动结构、相间接触等对流化床反应器的性能及产品的收率具有重要的影响，前人已对此开展了大量研究。气固两相流是一种复杂的动态时空多尺度结构，从单颗粒到宏观流动都表现为非线性、非平衡的特性。比如，单个催化剂颗粒内部孔道、催化剂表面等的流动，被界定为微尺度的流动，在设备尺度的宏观流动则被定义为宏尺度[1]，而气泡和聚团则是典型的介尺度结构。介尺度是介乎于微观和宏观之间的尺度，它的流体力学特性对传质、传热甚至流动等过程都有重要的影响。实现介尺度结构的识别与定量表征，建立准确的流体力学模型并对其进行预测具有重要意义。

1 介尺度流动结构

1.1 稀疏气固流中的介尺度结构

稀疏气固流中的介尺度结构出现在循环流化床、稀相空间、快速床和输送床中，主要以松散的颗粒聚团(cluster)形式存在。Chen等[2]发现，气固两相流之间之所以会产生高速滑落、固体混合以及向下流动等现象，是由于颗粒聚团一直在不断地形成和解体。Bi[3]对文献中报导的颗粒聚团进行了总结，提出共存在4种颗粒聚团，分别是cluster，streamers/strands，swarms和sheet。

Soong等[4-5]初次提出了稀相气固流中聚团的判别准则：①聚团内的颗粒固含率显著高于该处的时均颗粒固含率；②聚团的存在时间显著高于颗粒的随机波动；③聚团体积大于单颗粒体积的一到两个数量级，但远小于床层尺寸。对于此方法，当瞬时颗粒浓度大于临界浓度εpcr时，就认为在探头测试区域范围内出现了聚团。其具体的判断标准为:

(1)

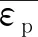
小波变换通过伸缩、平移运算功能可以对信号进行多尺度的细化分析，得到更准确的时频分辨率。随着计算科学的发展，小波分析在动态信号处理领域有了广泛的应用。在小波变换分析中，两个互补的滤波器可以产生A和D两个信号。A代表的是动态信号的近似值，是大缩放因子产生的系数，代表了信号的低频分量；而D则代表细节值，表示了小波分析中动态信号的高频分量，即小缩放因子所产生的系数。任意一个离散信号x(t) (t=1,…,N)，都是由小波基函数φj,k(t)和ψj,k(t)组成。其中的小波基函数是由尺度函数φ和母小波函数ψ通过伸缩变换和平移得到的，如式(2)、式(3)。

(2)

(3)

式中:k=1,2,…,N/2j，代表时间移位；j=1,2,…,J，代表转换层数。进一步，由式(2)、式(3)可以得到离散信号x(t)的近似系数和细节系数：

(4)

(5)

在此基础上，可以得到近似信号，其分解过程如图1。

(6)

(7)

其中，细节信号代表的频率范围是(fs/2j+1～fs/2j) Hz，近似信号代表的频率范围是 (0～fs/2J+1) Hz，如图1所示。

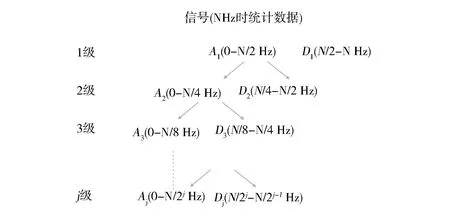
图1 小波分解过程示意图

Guenther等[10]和Afsahi等[11]对原始颗粒浓度信号进行小波分解的同时，还结合了50百分位标准，提出了提升管内颗粒聚团的确定方法；Yang等[12]采用小波分解方法，利用不同阶数细节近似信号包含的气固流动特征，区分提升管内的聚团和稀相；Chew等[13]在提升管中对B类颗粒的光纤信号进行了小波分解，发现聚团出现概率主要受位置影响，聚团持续时间和频率取决于颗粒性质和操作条件；Yan等[14]通过将小波分解与灵敏度分析法进行结合，将光纤信号进行解耦，并对聚团进行识别；Breault等[15]通过对原始电压信号进行小波分解，提出D3-D5可以表征介尺度。小波分析法本质上是将颗粒浓度信号解耦后，人为规定某个频段代表颗粒聚团，但目前尚未见到将解耦信号和聚团直接一一对应起来的直接证据。

1.2 稠密气固流中的介尺度结构及其识别方法

Toomey等[16]最早准确地概括出气固流化床的复杂流动情况，提出鼓泡流化床是由几乎不含固相颗粒的气泡相和处于起始流化状态的颗粒组成的乳化相所组成，即两相流动模型，如图2所示。该理论认为维持颗粒处于流态化状态所需的最小气体量为Qmf，此时所对应表观气速为umf，所有多余气体(Qg-Qmf)在通过床层的时候都是作为“气泡”的形式，并且该理论假设气固间相互独立、均匀分布且不存在相互作用。

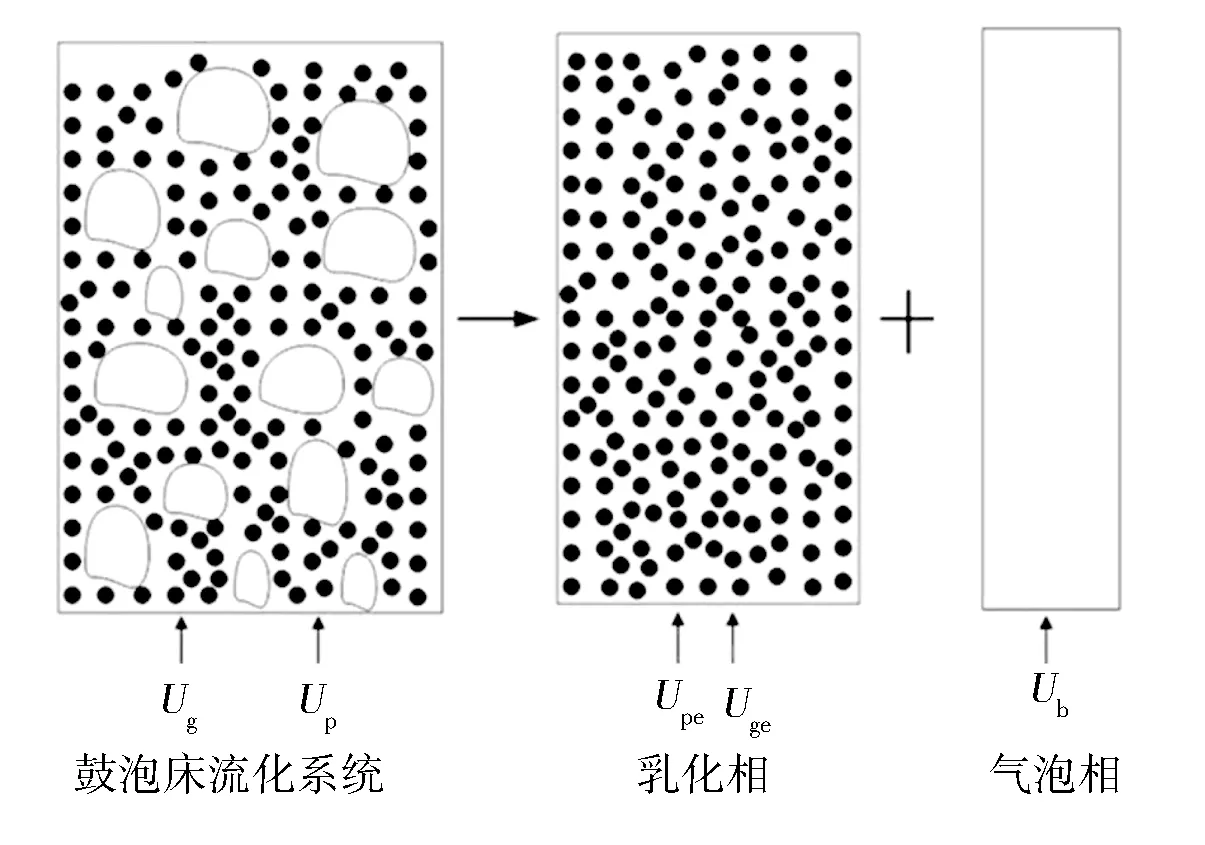
图2 经典两相流动结构示意图

研究结果表明[17-18]，这种假设与实际情况并不相符。气泡内不仅存在固体颗粒，并且颗粒浓度的分布是不均匀的，同时乳化相的固含率也并不完全等同于起始流化床层的固含率(εs,mf)，而是在其附近波动。Grace等[19]从能量的角度证实了处于均匀起始流化状态的乳化相是一个不稳定的系统；Lettieri[20]发现FCC颗粒流化床的带出速度远远大于单颗粒的自由沉降速度；Mostoufi和Chaouki[21]等人利用放射性粒子发现，鼓泡床中存在着颗粒聚团。根据以往的经验，研究者们只有在采用基于聚团的曳力模型对密相流化床进行数值模拟时，才能取得与实验结果更为接近的模拟结果[22]。在密相床，如鼓泡床和湍流床中，应用能量最小化多尺度模型可以将非均相流动结构分为3部分：乳化相，气泡相和介于两者之间的相[23]。Sun等[24]提出在密相流化床中存颗粒涡。颗粒涡是由气泡运动诱发的颗粒湍流结构。Sun等[24]使用连续小波变换方法分析颗粒涡的流动行为。结果表明，颗粒涡的时间尺度与小波尺度呈现线性关系。在气固流化床中，两相滑移速度会导致涡的运动、拟自由剪切效应以及循环流型，如气泡引发的相干结构和颗粒聚团。上述的各种事实，都间接表明了聚团的存在。但是到目前为止，鲜有对乳化相中颗粒聚团的直接测量结果的报道。

Liu等[18]分析了光纤脉动信号的概率密度分布曲线，发现空气-FCC催化剂流化床中密相的固含率在0.50～0.75范围内波动。因此根据颗粒流化的状态，提出乳化相中固含率高于εs,mf的部分为颗粒聚团(agglomerate)。颗粒聚团的体积分率随局部时均固含率的改变而改变。稠密气固流中的介尺度结构可以通过3结构模型来表述：含有颗粒的气泡、处于起始流化状态的乳化相和颗粒聚团。其中的乳化相代表的是除去气泡和颗粒聚团外的悬浮颗粒。颗粒聚团的内部处于未流化状态，但作为一个聚团和乳化相一同被流化。稠密气固流的介尺度流动结构如图3所示。

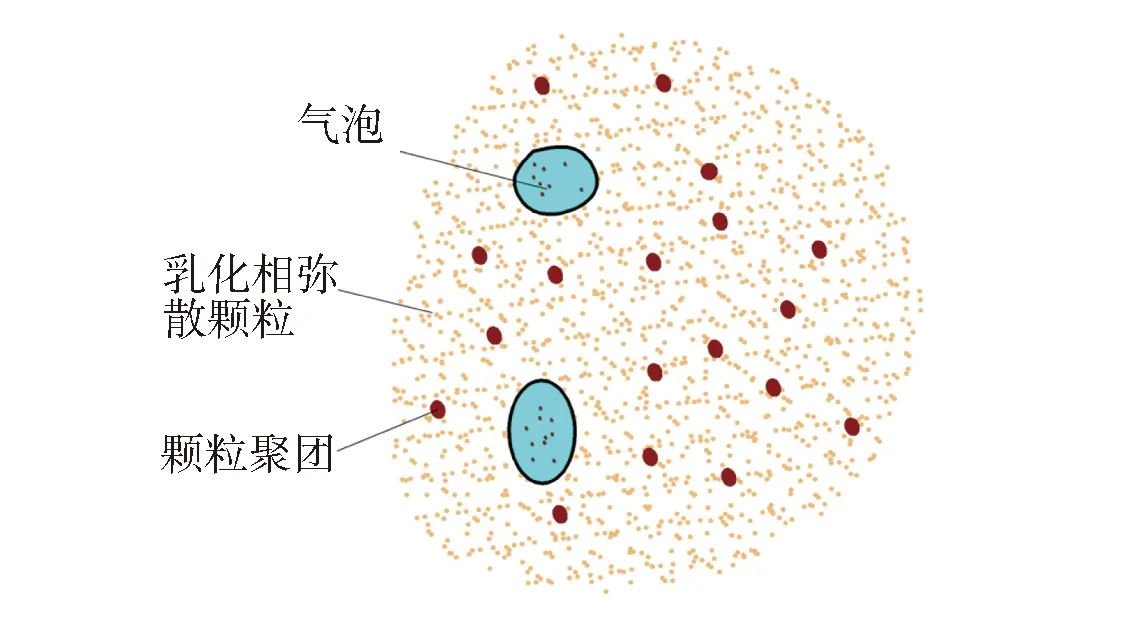
图3 稠密气固流的介尺度流动结构

由于实验技术的局限，尽管人们已经意识到稠密气固流中普遍存在介尺度的不均匀流动结构，但却难以对其中大量的气泡、颗粒及聚团的动态变化进行直接测量，因而也难以对介尺度结构动态变化有全面、直观的描述[25]。目前，气固流化床中介尺度流动结构的测量方法有：激光多普勒测速仪(laser doppler anemometer,LDA)[26]、相位多普勒颗粒分析仪(phase doppler particle analyzer,PDPA)[27]、高速摄影[28]及激光成像[29]、颗粒成像测速仪[30]、光纤测量法[13,31-32]等等。

LDA与PDPA法可以测量颗粒的浓度和速度，但是由于稠密气固流中大量存在的非测量颗粒目标会对测量结果产生极大的干扰，因而这两种方法仅适用于极稀的流场[26]。Lackermeier和Werther等[29]首次尝试通过使用内窥镜的方法，将激光引入床层内部，拍摄到了床层内部的影像。但是内窥镜本身尺寸较大，会对流场造成了一定的干扰。此外，该方法只能测量团聚物的表观行为，无法定量获得聚团内部的颗粒浓度等参数。高速摄影[28]、激光成像[29]、颗粒成像测速仪[30]等摄像类测量方法的优点是测量结果直观，并且通过二值化处理，可以将聚团与本底区别开，但是该类方法只能获得床层表面附近的流体力学参数，无法获得床层内部颗粒聚团的动态演变。由于多相流的非均匀非线性特征，流动结构不能仅通过时间或体积平均参数进行表征。目前，用来分析瞬态信号的方法已经有很多。Bai等[33]使用统计法和混沌分析法来研究流动结构；Liu等[34]使用电容层析成像(ECT)技术测量气体-颗粒间相互作用，颗粒边界相互作用以及气体对固体流动的影响，但其需要较高的空间分辨率；Roy[35], Kalo[36]， Larachi[37]和Jain等[38]使用放射性粒子追踪研究了多相流(RPT)技术，但它一次只能跟踪一个放射性粒子并且需要很长时间才能获得完整的流场。

与上述技术相比，光纤探针在研究气固流化床中的局部流动结构方面得到了越来越多的应用。通过显著缩小光纤探针的尺寸，尤其是探针尖端的尺寸，可以将其对流场的干扰减小到忽略不计[31-32]。Wang等[39]通过光纤探针测量，得到了在鼓泡床与湍流床中固含率时间序列信号，并对信号的概率密度曲线进行了统计分析，发现其为双峰分布，气泡相对应固含率较小的峰；乳化相对应固含率较大的峰。此后，研究人员开始尝试用不同的模型去拟合固含率概率密度曲线来得到稀相和乳化相的流体力学参数，并且从中分析两相所占的比率随着空间位置、操作条件等变化而产生的变化规律。比如：Cui等[40]通过Gamma分布函数对其变化曲线进行了拟合，发现在峰值处的拟合值与实验值吻合较好；Wang[39]等尝试对两相分别进行拟合，分别对气泡相进行了对数正态分布函数拟合，对乳化相进行了正态分布函数拟合；Cui等[40]针对其变化归路进行分析，提出了一个概率模型，用于描述气泡相和乳化相，为之后研究两相结构做出了理论铺垫。

对于确定气固流化床中稀相、密相的分界标准，定义方法有很多，主要可以分为以下几种：

1)中点法[41]：将两峰的中点设置为稀相、密相的分界点，这种方法的优点是操作简单，缺点是误差相对较大。

2)最小值法[41]：找到两峰间的最低点，将其设为稀相、密相的分界点，这种方法的缺点是当曲线较平缓时，很难通过观察找到最小值。

3)插值法[42]：这种方法的分界标准是将最大振幅与最小振幅之差的0.05倍定作分界点，缺点是在取值上没有一定的标准，因此可能并不适用于其他流化床的光纤测量。

4)半峰法[43]：假设峰值两侧的曲线是呈对称分布的，因此可以通过映射找分界点。具体计算方法如图4(d)所示。

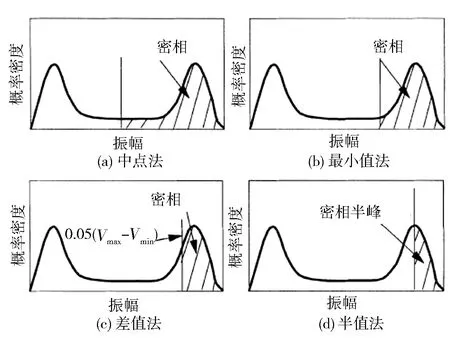
图4 流化床内区分密相与稀相的方法[41]

5)3倍标准差法[18]：认为密相峰符合高斯分布，并以均值加3倍标准差为分界点。

Bi等[41]采用的实验介质是FCC颗粒，分别采用5种方法分析实验数据，在同一套直径为100 mm的流化床中进行实验，并通过数据得到相对应的阈值，计算了稀相的体积分率，结果如图5所示。虽然是同一组数据，但是使用不同的分析方法，得到的稀相体积分率结果也会相差很大。因此，有必要找到一个能准确估计稀疏、稠密两相流动参数的模型。

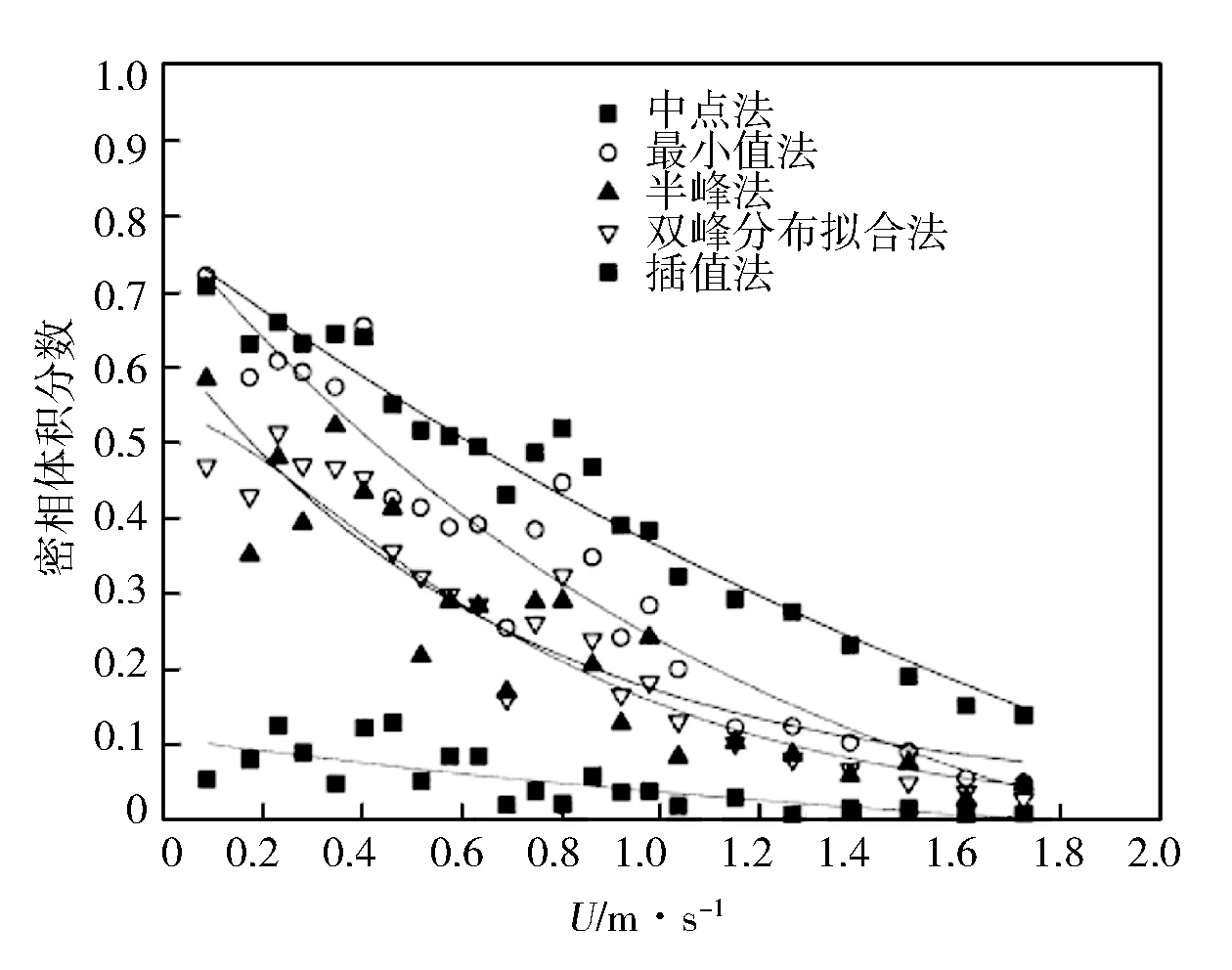
图5 基于不同阈值方法得到的稀相体积分率对比[41]

Bi等[44]为了解决这一矛盾，提出了一个对循环流化床、鼓泡床和湍流床均适用的两相结构的理论模型，如式(8)-式(13)所示：

εs=f1εsb+(1-f1)εsd

(8)

(9)

(10)

(11)

εsb=S×Sk+2εs-εsd

(12)

f1=(εs-εsd)/(εsb-εsd)

(13)

式中：εs，εsb及εsd代表局部固含率以及稀密相的平均固含率；f1代表稀相所占分率；S和Sk分别代表瞬时固含率标准偏差及其偏斜度。

Zhu等[45]发现Bi的模型使用4个统计矩来计算3个流体动力学参数，这可能导致两种方法计算得到不同的结果。因此，提出了一种选择统计矩的方法，即当|S|<1.5或K<4.5时，平均固体含量εs，标准偏差σ，偏度S的统计矩组合会得到最优结果。这种方法避免了任意选择阈值并且可以精确计算3个流体动力学参数。

由式(8)-式(13)可以发现，此模型可以经过计算得到稀密两相的平均固含率以及各自所占的体积分率，因此不需要人为选定阈值，因此很好地解决了使用不同方法所带来的巨大差异的问题。但是通过此模型无法得到其他流体力学参数，包括气泡的尺寸分布、出现频率及运动速度、稀密两相的固含率分布等。

2 流化床中气泡行为的研究

气固流化床中气泡的特性是气固流化床反应器设计、操作和放大的重要参数之一，可以反映床层的流型结构和气固间的接触效果，并且直接影响着流化床的传递特性，例如颗粒的混合、传热和传质等。因此，认识气固流化床内流动特性和流化质量的基础和前提是深入了解气泡行为。

2.1 气泡的特征

经典理论认为，在鼓泡床中，气泡一般是椭球形或者为球形。气泡上半部分为球冠形空穴，其内几乎不含固体颗粒，而下半球则为尾涡，包含着大量固体颗粒。尾涡是位于气泡底部并且随气泡一起上升的颗粒群，对流化床中颗粒的运动和稀相自由空域的行为有着重要的作用，它是流化床内颗粒循环的主要动力。气泡的特征参数与流化气体的气速有着直接的关系。当最小流化速度或最小鼓泡速度小于流化气速时，部分“多余”的气体就会以气泡的形式穿过床层，因此形成了鼓泡流化床。

气体示踪实验表明，流化床反应器中气泡的结构除了尾涡和球冠空穴，还会在特定情况下在气泡外形成一层气晕，也称为气泡晕。这是一层包围气泡的气膜，当气泡周围的颗粒在气泡的上升速度高于乳相中气体的速度时，就会夹带部分气体，沿气泡边界迅速向下流动，重新返回到气泡底部，形成气泡晕。气泡晕的存在使气泡相的识别变得非常困难，由于气泡晕的固含率介于气泡和乳化相之间，由气泡到周围的乳化相，固含率的变化较为平缓，往往找不到清晰的分界点或阈值将气泡相和乳化相分隔开来。文献中很少见到关于气泡阈值或其与气泡尺寸等参数关系的报道，这导致在数值模拟研究中，人们往往只能人为设置气泡阈值。例如：Kuiper等[46]将气泡阈值设定为0.15；Witt等[47]认为气泡的阈值为0.20；Halow等[48]设置气泡阈值为0.25～ 0.30；McKeen[49]将气泡阈值定为0.15～0.30。

气泡的形状并非一成不变，在上升过程中，气泡之间会相互碰撞，形成气泡聚并生成大气泡或是破碎成小气泡。与此同时，气泡的形状也可能发生变化。气泡破碎与聚并之间的动态平衡将决定流化床中气泡平均尺寸和最大稳定气泡尺寸。

2.2 气泡的尺寸

流化床内的气泡尺寸是决定流化床反应器内气固接触面积的重要参数，但由于实验条件和床层结构存在差异，很多研究气泡聚并的机理和气泡聚并后得到的气泡尺寸也各不相同。测量气固流化床内气泡尺寸的测量方法主要有两种，一种是如光纤探针法的侵入式(Intrusive technique)；另一种是如压力脉动法的非侵入式(Non-intrusive technique)。

图6给出了光纤探针法测量流化床内气泡尺寸的原理：当气泡从下到上依次经过两根平行光纤探针的探头时，所产生的两组信号间存在一定的时间延迟。Liu等[50]曾给出计算气泡弦长db的公式：

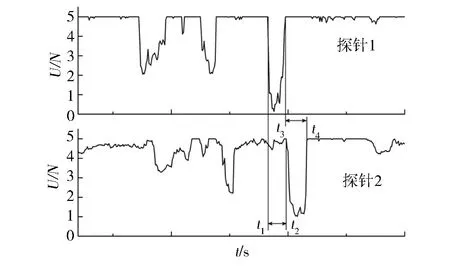
图6 气泡通过光纤探头时产生的信号[50]

(14)

(15)

式中：d表示两根平行的光纤探针探头的间距；ub表示气泡通过光纤探针的平均速度。由式(14)、式(15)可知，通过延迟的时间、两探头之间的距离和气泡的持续时间就可以计算出气泡的尺寸。

20世纪50年代，Yasui和Johanson[51]就已经通过光导探针对气泡的流动特性进行了研究，并根据实验数据回归了计算气泡尺寸的经验式。而后，Werther等[52]在实验时固定了光纤探针探头的测量高度，发现随着床层直径的减小，床层内的气泡尺寸会随之增大。根据实验测量的结果，他们提出：气泡尺寸的增大是由于气泡的聚并造成的假设，与此同时还回归模拟了大直径流化床反应器床层内的气泡尺寸关联式。Darton等[53]基于这一假设，得到了气泡尺寸的经典关联式：

(16)

此模型假设气泡在流化床内的上升过程中只存在聚并增大的现象，并且忽略了气泡与气泡之间的相互碰撞和分裂。而后，Choi等[54]在碰撞理论的基础上，对气泡尺寸关联式进行了进一步改进，使其可用于各类颗粒，修正后的关联式为

(17)

Horio等[55]认为在Geldart A类床中气泡稳定的尺寸是由于连续的聚并和破裂而形成的，并在此假设基础上推导出气泡直径关联式：

(18)

流化床内压力脉动信号包含差压压力脉动信号和绝压压力脉动信号。为比较两种压力信号，Roy等[56]分别测量了在流化床反应器内同一个位置处的差压压力脉动信号和绝压压力脉动信号的振幅，发现在相同的测量频率下，压力脉动的幅值差异很大。经过分析，Roy认为差压压力脉动信号只能反映测量间距内压力脉动的特性，而绝压压力脉动信号则反映的是全床所有压力脉动源的特性。

Bi等[41]在进行大量的研究后，发现压力测点间气泡的平均尺寸与压力测点间差压压力脉动信号标准偏差存在以下关联：

(19)

通过进一步分析，发现在小间距(0～200 mm)测量范围内测量得到的差压脉动信号过滤掉了大量的压缩波信号，使得局部气泡波信号保留了下来。

Van der Schaaf等[57]通过比较床层内某处的绝压信号和分布器风室中的不含有气泡波组分的绝压信号的频谱特征的相干性，将床层内测量得到的绝压信号分为不相干部分(IOP)和相干部分(COP)两部分。而气泡波组分更多地被保留在了不相干部分。因此，可以通过对绝压压力脉动信号中的不相干部分进行计算来确定气泡的平均尺寸：

(20)

综上所述，式(19)和式(20)都可以通过压力脉动信号来计算床层内气泡的平均尺寸。但式(19)和式(20)都没有给出比例系数，因而难以根据压力脉动信号定量计算气泡的尺寸。Liu等[50]在内径为0.29 m的流化床内对压力脉动进行了测量，并将式(19)和式(20)两种方法得到的气泡尺寸与光纤探针测得的气泡尺寸进行了比较，发现采用不相干分析方法得到的气泡尺寸比绝压分析法得到的大。

3 流化床中颗粒聚团的行为研究

流化床内形成的颗粒聚团会对反应器中的一些关键操作特性参数例如床层密度、传热和传质、压降、反应的动力学以及轴向的气固混合[58]等产生重大的影响。通过对颗粒聚团特性的研究，不仅可以更加深入地理解流化床反应器中的传质、传热与反应规律，而且有助于预测流化床内轴、径向气固流动形式，从而提高反应器的反应效率、预测和消除工业装置中的腐蚀。因此，对颗粒聚团的研究尤为重要。

3.1 颗粒聚团的形成机理

流体流化是颗粒间作用力与两相曳力共同作用平衡的结果。颗粒聚团并非一种单一的力作用的结果，而是几种力及环境共同作用的结果。对于A类颗粒来说，两相间的曳力和颗粒间作用力占主导时均可形成颗粒聚团。其中颗粒间作用力包括非弹性颗粒碰撞力、静电力、毛细管力以及范德华力等[59]。范德华力是较为主要的颗粒间作用力，两个球形颗粒间的范德华力可表示为[60]：

(21)

式中：a为颗粒表面之间的间距，其值在1.65 A°～4.00 A°之间变化；R为颗粒的半径。Seville[60]和Molerus[61]认为R并不是简单地等于颗粒的半径，而是与颗粒表面的粗糙度或接触点局部曲率密切相关。Seville[60]计算了一种密度为3 000 kg/m3的颗粒，发现若取R为颗粒半径，当颗粒半径为0.5 mm时其所受到的范德华力约等于自身的重力，这显然是不合理的。若采用Krupp[62]的测量结果，R的取值应在0.1 μm左右，计算得出，当颗粒半径为50 μm左右时，颗粒所受到的范德华力约等于自身的重力。其他颗粒间作用力的相对大小可见图7。

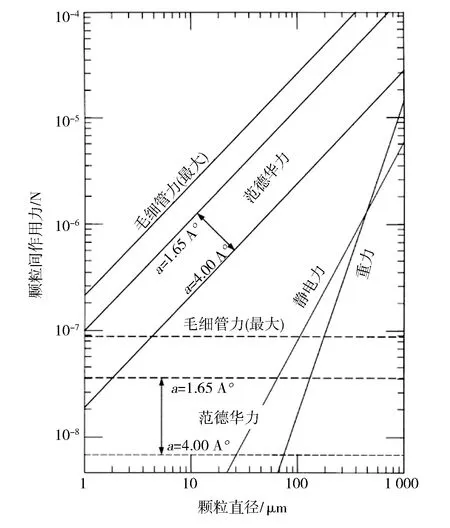
图7 颗粒间作用力大小的比较[60]

3.2 稀疏气固流中的颗粒聚团

Horio等[63]使用高速摄像机在循环流化床反应器中的床层截面拍摄到了颜色较深的团聚物，因此他用“denser islands of particles”和“cluster”等词语来定义颗粒聚团。Yerushalmi等[64]使用“streamer”，“strand”，“ribbon”和“dense packet”来表述提升管中的颗粒聚团，此后还使用了“swarm”和“sheet”。Bi等[3]对二维循环流化床反应器的提升管中的颗粒聚团进行了归纳总结，按照颗粒聚团的尺寸、形状和存在位置的不同分成了以下几类，如表1[3]所示。

表1 提升管反应器中的颗粒聚团的分类

在稀相流化床中，聚团的特征为连续固相，所以其平均固含率受到气固两相互相作用的影响很大。Chen[65]认为颗粒聚团的固含率不是一个定值，而应该随着空间位置和气固流速的变化呈现概率分布，并且操作气速的增大会使固含率显著降低。根据Soong等[4]总结的经验数据，提出了一个在预测提升管中聚团固含率轴向分布时适用的模型：

εsc=εmf[1-(1-εs/εmf)3.4]

(22)

式中：εs代表局部的时均固含率，εmf代表起始流化固含率。

Lin等[17]通过研究观察得到，近壁区处εsc在同样的表观气速下越接近壁面处，其数值越大，然而在FCC提升管内的横截面的其它位置处，εsc都近似为常数。当临界输送速度utr大于表观气速时，εsc近似等于起始鼓泡乳化相的固含率，为0.68，此时，不管在何种操作条件和任意径向位置上，颗粒团都可通过传统两相理论中的起始鼓泡乳化相来表征；但是在高速提升管中，只有在近壁区存在颗粒团，因为只有在近壁区，局部气速才非常小，颗粒团才能保持稳定状态。因此，可以认为起始鼓泡乳化相是一种稳定的固体聚团的形态。

表2[9]给出了研究者们关于聚团内固含率的研究数据，从表2中可以看出，颗粒聚团的固含率范围为0.05～0.50。

表2 文献中聚团内平均固含率数据

Matsen[68]发现聚团尺寸依赖于颗粒性质。表3给出了文献中关于聚团尺寸研究的结果。

表3 文献中关于聚团尺寸的研究结果

除了上述实验的测量结果，研究者还总结了一些其他经验关联式并进行了系统分析。邹斌等[73]通过对实验数据进行拟合得到了一个经验关联式，即用局部颗粒浓度与初始流化空隙率构成的函数来表示团聚物的直径，关联结果和实验结果的误差在10%以内；白丁荣等[74]用半理论半经验方法提出了一个可以用于计算团聚物直径的关联式；Gu和Chen[75]基于Yerushalmi的理论研究，用聚团物公式进一步拟合，得到了一个简易的表达式；而后，Gu等[72]假设固相压力等于聚团物重力，并推导出一个用于描述聚团物直径的模型；Harris等[58]综合前人的研究结果，通过关联得到了一个公式，用于代表截面平均颗粒浓度，但其缺点是此公式只能预测边壁附近的聚团物直径。表4给出了5种经验关联式：

表4 文献中聚团物的直径关联式

3.3 稠密气固流中的颗粒聚团

Liu等[18]采用光纤探针，在一套直径为300 mm的环流反应器中对FCC颗粒在操作气速ug=0.10～0.54 m/s范围内进行了测量。如图8所示，根据颗粒流化的状态，以起始流化时的固含率εs,mf为分界点，将密相进一步分为较稀和较密两个部分。较稀的部分代表气泡顶部、分散的悬浮颗粒和尾涡，他们都处于流化状态，实际上，就是经典两相理论中所定义的乳化相；较密的部分代表颗粒聚团，处于未流化状态。在光纤脉动信号中，聚团的识别判据如下：

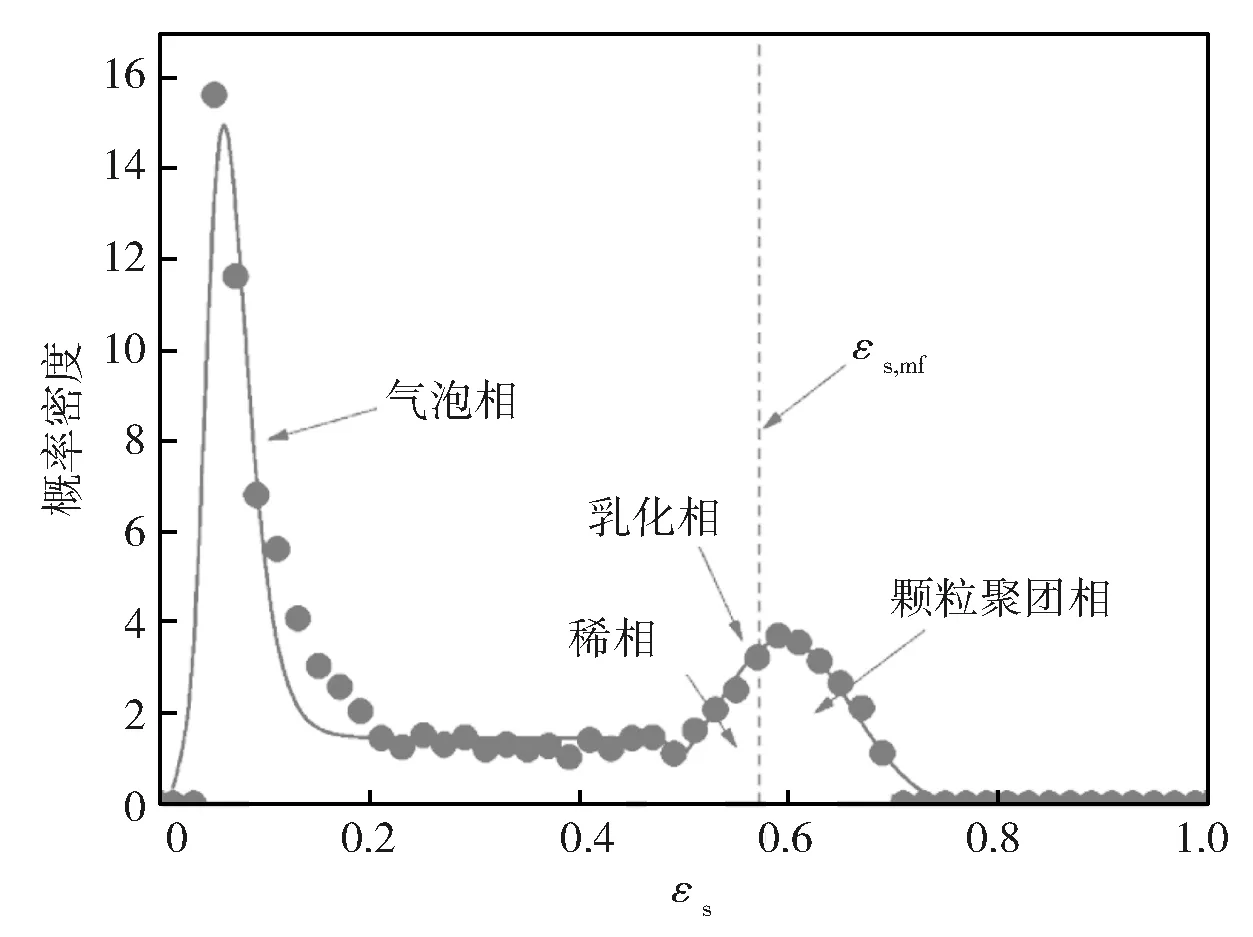
图8 稠密气固流中光纤脉动信号的概率密度曲线

1)聚团的固含率大于起始流化状态下的固含率εs,mf；

2)密相的固含率脉动幅值大于背景颗粒的随机脉动幅值；

3)在采集空间内固含率有明显的增加。

经测定，颗粒聚团直径为1.19 mm，是颗粒平均粒径的18倍。Cocco等[76]用高速摄像机分别在聚乙烯颗粒 (ρp=400 kg/m3) 和FCC催化剂颗粒 (ρp=1 500 kg/m3) 流化床中进行拍摄，发现流化床中41%的FCC催化剂作为颗粒聚团存在，平均聚团尺寸为21±1.7个颗粒。在自由空间中，聚乙烯颗粒的聚团浓度可以达到FCC催化剂颗粒聚团浓度的两倍，且聚团尺寸大约也比FCC催化剂颗粒聚团的尺寸大一倍。由此可以看出，聚团的形成不仅取决于颗粒的量，还跟颗粒密度等本身的性质有密切关联。同时，采用高速摄像机及内窥镜拍到流化床中心处的颗粒聚团(如图9)，这无疑为稠密气固流中颗粒聚团的存在提供了直接证据。

图9 流化床内FCC催化剂颗粒图 (16 cm，0.61 m/s)

McMillan[77]等在Cocco的基础上发现颗粒聚团更多地由细颗粒组成(小于44 μm)，或者细颗粒吸附在大颗粒上，几乎没有大颗粒单独组成聚团。流化床中的颗粒聚团尺寸远大于自由空间内的聚团尺寸，如图10。

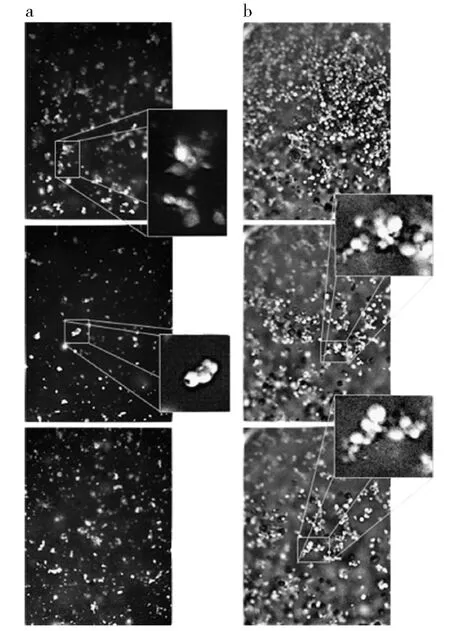
图10 颗粒聚团在(a)自由空间及(b)流化床中

Duan等[78]将FCC颗粒添加到纳米颗粒中，发现粗颗粒会发生碰撞并进入颗粒聚团，导致聚团更松散、更小，进而提高了流化性能。Chavan[79]发现在液固系统中，颗粒聚团的当量直径和输入的能量成反比，其形式可表示为：

(23)

式中:dagg1为颗粒聚团直径；Ninput为气体穿过颗粒组成床层的单位质量总能耗，可表示为Nst和Nd的和。其中Nst为悬浮和输送单位质量颗粒的总能量；Nd为颗粒、聚团碰撞、加速、摩擦以及气泡的破碎、加速等消耗的能量[78]。在此基础上，石战胜[80]提出了基于EMMS 方法的 EMMS / bubbling 稳态模型应用于气固鼓泡流化床，此模型没有原 EMMS 模型里面的聚团来作为介尺度结构，而是用气泡替代，因此，鼓泡流化床也相应地分成了3个子相，即乳化相、气泡相以及相间相。基于子相动力学的方程可以用悬浮和耗散能量的子系统，悬浮颗粒消耗的能量趋于最小(Ns→min)的稳定性条件进行封闭。

3.4 颗粒聚团尺寸预测模型的研究

聚团尺寸是气固流化床中关键的流体动力学特征参数之一，对流化质量有重要影响。已经提出的各种用于计算粘性颗粒流化时聚团平衡尺寸的模型大多是基于力平衡。

Chaouki等[81]遵循Molerus[61]的理论，并提出由流体施加的力(近似为净重力)等于颗粒间作用力，如：范德华力；类似地，Iwadate等[82]基于由气泡和聚团-聚团内聚破裂力引起的床膨胀力平衡来预测平衡聚团尺寸；Turki等[83]假设凝聚力主要为范德华力，并且考虑了控制聚团形成的各种力来估算团聚体的大小；Zhou等[84-85]考虑了气泡的流体力学特性，并根据作用在聚团上的力进行分析，提出了力平衡模型，建立了颗粒聚团的作用力平衡模型：

(24)

式中：Fy为曳力；Fva为粘性力；Fg为重力-浮力作用力；Fc为碰撞力。通过建立二元方程对平衡模型进行求解，此模型得到的平均聚团尺寸与实验结果相一致，证明了模型的可靠性。此外，他们还研究了影响聚团尺寸的参数，发现较高的气速和流体密度，较小的聚团间粘附力和碰撞力可以有效减小聚团尺寸。然而，他们假设两个聚团之间的碰撞是完全弹性的，忽略了碰撞的能量损失。

另一方面，能量平衡模型也被用于估计聚团的大小。Morooka等[86]首先提出了能量平衡模型来确定平衡聚团尺寸，假设当流体剪切能Edrag和碰撞能Ecoll产生能量的总能量大于粘附能Ecoh时，聚团倾向于破裂。因此，由能量平衡确定的临界聚并点为：

Ecoll+Edrag=Ecoh

(25)

然而，能源损耗仅局限于特定聚团的破碎。Matsuda[87]为聚团的破碎提出了一个改进的能量损耗模型，该模型提出颗粒的破碎能耗应考虑单位重量聚团所需的能量。Xu等[88]基于聚团碰撞能、粘附能和振动能之间的能量平衡来预测聚团尺寸。但是，他们的模型忽略了流体剪切产生的能量影响。Zhou等[89]根据聚团碰撞能、振动波产生的有效能、流体力学剪切产生的能量和粘附能之间的能量平衡，提出了一个用来预测聚团尺寸的模型。

1)碰撞能

Xu[88]假设碰撞过程中碰撞力保持不变，当Φ=1时碰撞能

(26)

Xu[88]定义相对速度

(27)

通过比较预测结果和实验结果，在Xu的模型中λ经验假设为0.1。

Zhou[89]认为碰撞的聚团在运动中可能加速或减速，碰撞能

(28)

2)剪切能

聚团的剪切力已由方程 (24) 给出，由剪切力得到的剪切能

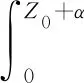
(29)

将方程 (24) 代入方程 (29) 得

(30)

3)粘附能

由于存在像范德华力这样的颗粒间作用力，颗粒很容易团聚。同时，当聚团相互碰撞时，也可能分裂成较小的部分。聚团破碎时需克服聚团内部粘附能Ecoh。假设破碎过程中粘附力恒定，粘附能[89]

(31)

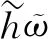
在研究两种粘性颗粒的碰撞动力学时，Yang[90]提出了团聚或分离的准则和碰撞后颗粒速度的关联式；Moseley等[91]提出了一个应用于表面粘附弹性颗粒的双颗粒碰撞模型；Gidaspow[92]也对两个颗粒的碰撞动力学进行了研究，并且给出了碰撞前后颗粒速度的关系。但是，他们的研究仅限于颗粒间的碰撞，并不包括聚团间的碰撞动力学。

4 结论

本文对近年来气固流化床中介尺度流动结构的基础研究进行回顾，分别阐述了稀疏气固流和稠密气固流中介尺度流动结构的识别方法，重点阐述了典型介尺度流动结构气泡和聚团的形成机理、流动特性、特征尺寸和预测模型。前人对稀疏相流化床中介尺度流动结构的研究已较为深入，但对稠密气固流中聚团的研究大多局限于定性的研究，鲜有对稠密相流化床中介尺度流动结构的直接测量结果的报道，因此难以定量获得介尺度流动结构如气泡和颗粒聚团的流体力学特性参数。在今后的工作中，需要在稠密气固流化床中介尺度流动结构的识别与表征、定量测量等方面进一步展开研究。