让“规律”教学充满数学的魅力

张新培

【摘 要】“探索规律”是小学数学教材中重要的教学内容之一，涉及数、式、形等方面的内容，对学生的思维能力要求较高。在数学课堂教学中，教师应以相关内容为载体，让好奇成为探索规律的引擎，引导学生探索;让深度思考解开规律之谜，挖掘知识中隐含的规律与变化趋势;在多元表征中，体会规律之美，变传统的单向思维为双向的思考，实现规律的吸纳、理解和应用，建立良好的数学认知结构;在变与不变中，体会规律之魅，真正让数学课堂彰显生命的活力和精彩。

【关键词】小学数学 课堂教学 探索规律

苏教版小学数学教材对“探索规律”的内容进行了合理选择和精心设计，让学生经历发现规律、探索规律、理解规律、运用规律的全过程。何为规律？就数学知识而言，主要是数和形在变化过程中，始终保持不变的特征或关系，规律往往存在于变化之中。在课堂教学的过程中，教师应从变化的角度，引领学生研究数量关系和图形特征，掌握知识的本质内涵，培养学生抽象、概括、推理的能力，不断提升其思维品质，建构有“经历”的数学课堂，让学生在有趣中体会数学知识，在探究中感受数学的魅力。下面笔者结合四年级上册《商不变规律》一课的课堂教学，探讨“规律”教学的策略。

一、让好奇成为探索规律的引擎

梁晓声说，儿童的学习，先要“有意思”，再求“有意义”。学生喜欢的数学课堂也一定是充满趣味的课堂，而好奇最能激发学生对未知探索的趣味。

在教学《商不变规律》一课时，教师创设了这样的情境：学校准备进行团体比赛，体操队有40人，舞蹈队有20人，体操队的人数是舞蹈队人数的几倍？[40÷20=2。]在进行表演时，每个队员要举两面彩旗，体操队准备的彩旗是舞蹈队彩旗的多少倍？[（40×2）÷（20×2）=2。]每个队员要准备4个气球，体操队准备的气球是舞蹈队气球的多少倍？[（40×4）÷（20×4）=2。]在进行队形变化时，每4个同学拉成一个心形，体操队拉成的心形是舞蹈队心形的多少倍？[（40÷4）÷（20÷4）=2。]如果时间许可，教师还可以举出很多的算式，结果都是2。既然结果都是2，那是偶然，还是其中藏着秘密呢？学生的好奇油然而生。

上述过程，不露痕迹地把学习藏在“饶有趣味”之中。教师从学生的生活入手，精心创设情境，放大“冲突”，40÷20=2，很正常;（40×2）÷（20×2）=2，两个算式答案一样也是常有的事;（40×4）÷（20×4）=2，（40÷4）÷（20÷4）=2……好多好多的算式都可以是2，这里面一定有规律可循。这样的设计大大激起了学生的好奇心，将他们的注意力引向规律探索，并使学生产生探索规律的强烈期待，就像好的引擎一样，将澎湃发力。

二、让深度思考解开规律之谜

数学教学一定要有数学的味道，要体现数学的本质。要在揭示规律的过程中，让学生较为深入地领悟数学的内涵，体会数学的魅力。在这样的理念指导下，在《商不变规律》一课的教学中，教师同样不能“和盘托出”，应让出课堂的时间和空间，让学生的思维深度参与，进行自主探索，在学生获得“现实”与“直观”的支撑后，教师应引导学生尝试探索规律，解开规律的秘密。

师：同学们，刚才我们觉得很好奇，为什么这么多算式答案都是2呢？我们应该如何开启探索之旅呢？

生1：刚才那么多算式，我发现了他们都有40和2。

生2：我发现这些算式最后都是做的除法。

生3：那么多算式有没有什么办法让我们看得清楚一些呢？

師：同学们的想法都很好，都是在用数学的方法来探索其中的秘密，那我们能把刚才的算式列成表整理出来吗？

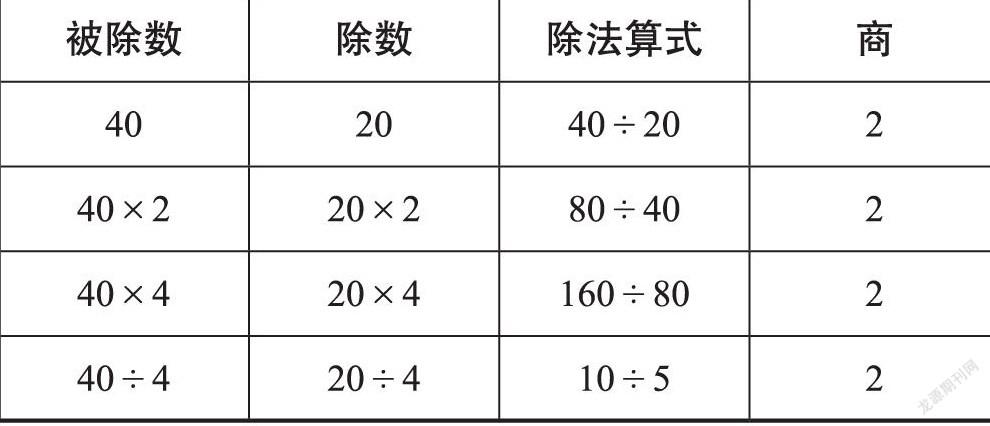
在师生的共同交流下，整理出如下表格：

被除数 除数 除法算式 商

40 20 40÷20 2

40×2 20×2 80÷40 2

40×4 20×4 160÷80 2

40÷4 20÷4 10÷5 2

师：整理到表格中，然后看看有什么发现。

在学生们整理好表格后，教师让学生观察表格，说一说有什么发现。学生们发现表格中的第三、四行，被除数和除数都是同时乘一个数，而第五行是被除数和除数同时除以4。在此基础上，学生们提出了猜想：在除法算式中，被除数和除数，同时乘以或者除以同一个数，商不变。

上述环节，因好奇，学生主动投入探索规律中，他们自觉运用比较来发现算式的相同和不同之处，用表格来整理信息。在此基础上，让学生再进一步观察、猜想，使规律变得具体化、直观化。在这过程中，学生深度思考着，不断演绎、推理着。这样的数学课堂可以充分挖掘教材中隐含的深层次的目标，激发学生的学习兴趣和学习主动性，启迪发展学生的数学思维，促使学生形成牢固、完善的认知结构，让学生在潜移默化中去领悟并内化为数学思维的品质。数学特有的味道彰显其中。

三、在多元表征中，体会规律之美

在学生经历探索发现规律后，学生对规律的理解常常是很有个性化的。因此，在课堂教学中，教师不要忙于归纳、总结，应让学生运用自己的方式表达对这个规律的理解，这种表达既是个性化的，更是多元化的。

下面四幅图是在课堂中收集到的。图1和图2具有普遍意义，学生模仿了探索过程中的表格呈现，虽然看起来没有个性，但也让学生感受到所发现的规律具有普遍的意义。图3中，学生通过倍数的比较，发现3组图中一组的方块个数是另一组方块个数的2倍。图4中，学生通过画长方形图发现，当长÷宽都等于3时，虽然图形在变化，但形状不变。这些多元的表达和交流，大大丰富了学生对这个规律的理解。从中，也让学生深深体会到了“商不变规律”内在的结构美，渗透了变与不变的辩证思想，也使所学规律真正在学生的头脑中扎根生长。

四、在变与不变中，体会规律之魅

学生掌握所学规律后，并不是学习过程的结束，教师应为学生引入实际问题，让学生在运用知识的过程中，展开深层次发展的学习活动，升华对所学规律的认知。然后，通过一些变式性训练，让学生形成结构化的认识。在这样的过程中，不仅可以帮助学生提升学习的境界，进一步提升归纳演绎、猜想验证的能力，还可以帮助学生感受商不变规律与数学应用的关系，形成各种有价值的感悟，体验所学规律的价值。

在探索出商不变规律后，笔者为学生设计了这样的练习：

540÷30=54÷（ ）=（ ）

6000÷60=（ ）÷6=（ ）

a÷b=3      （a×__）÷（b×__）=3

在学生充分交流后，讨论：这里可以填任何数吗？为什么？

一石激起千层浪，这个问题立即引发了学生的思考，学生认为：如果被除数或除数同时乘0，被除数或除数就都变成了0，而被除数或除数同时除以0，就没有意义了。此时，学生刚刚以为对规律的认识已经到位，通过这个问题的讨论发现，原来这个规律还有限制条件。

那么这个规律仅限于此吗？这时教师出示下面两组题：

根据每一组第一题的得数，直接写出每一组下面两题的得数。

（1）80÷4=20         （2）77÷3=25……2

800÷40=                 770÷30=

8000÷400=                7700÷300=

第一組题目，学生直接运用商不变规律作答，强化学生对所学知识的理解。在解答第二组题目的过程中，学生们认为第一组3道题目的商都是20，第二组3道算式的商自然应该都是25……2。显然，770÷30和7700÷300这两道算式的这种结果是不对的，教师没有直接指出，而是让学生通过验算发现错误，也引发了学生的认知冲突：这是什么原因呢？学生们一探究竟，最终得出了错误的根源：被除数和除数同时乘或者除以一个相同的数（0除外），如出现不完全商，它的余数是变化的，余数也要乘（或除以）这个数。

上述环节，在学生们探索出规律后，教师为学生设计了富有针对性的练习，故意让学生在变式练习中出错，并让学生自省、顿悟，探寻知识的内涵，提升思维的深刻性，帮助学生形成体系化的认知网络，促进课堂教学效益最大化。

总之，规律探索是小学数学课堂的重要教学内容，也是培养学生归纳推理能力的有效途径。在课堂教学中，教师应根据教学内容，精心设计探索规律的活动过程，体现探索规律的教学价值，真正让学生享受有味、有度、有质的数学学习过程，实现智慧生长，演绎出别样的精彩。

【参考文献】

[1]邱晓军.小学数学“探索规律”的教学价值解读[J].河北教育（教学版），2007（10）.

[2]刘久成.小学数学“探索规律”的内容设计[J].小学教学研究（教学版），2010（10）.