创新应用巧建模 回归基础探本质

孔繁晶

摘  要：2021年全国新高考Ⅰ卷第16题以“新、巧、活”的特征引起广泛关注. 针对这道“材料在外、考点在内、考查思维、体现能力”的数列创新题，以“读—探—猜—定—求”五步，探究其建模、解模的过程，并结合学生在答题中的困境，评析试题考查的重点与难点，提出相应的教学建议.

关键词：数列;创新试题;教学建议

作为一类离散函数，数列是刻画离散过程的重要模型. 它既是高中数学中的主干知识，又是高等数学的研究对象，其中蕴含了丰富的数学思想与方法，是培养学生数学学科核心素养的重要载体. 因此，成为历年高考的重要考点之一.

近年来，数学学科高考命题工作一直坚持“重思维、重应用、重创新”的思路与方向. 2021年全国新高考Ⅰ卷第16题是一道数列创新题，秉承这一理念命制，引起了广大数学教育工作者的关注.

一、试题呈现

此题以传统文化中的剪纸艺术为材料，背景新颖，蕴含丰富的人文价值;题干设置和问题提出简洁不冗长，方便阅读;因是折纸要求，可操作性较强，学生可以动手尝试、寻找思路;通过特例启发学生构建适合的数学模型，解决求和问题，综合考查学生数学阅读、逻辑推理、数学建模和数学运算等素养. 综上，确定此题是一道内涵丰富的优质试题.

二、解法探究

针对这道“材料在外、考点在内、考查思维、体现能力”的试题，笔者结合学生答题中的困境，以“读—探—猜—定—求”五步，探究其建模、解模的过程.

1. 读

拨开背景材料的层层迷雾是发现数学问题、寻求解决办法的关键. 因此，读懂题意就是踏上解题征程的第一步.

首先，粗读. 确定此题的核心是折纸问题，折纸的方式是依次对折，研究对象是对折多次后形成的不同规格图形的种数和面积总和. 猜测种数与面积之间存在规律，可能是数列问题.

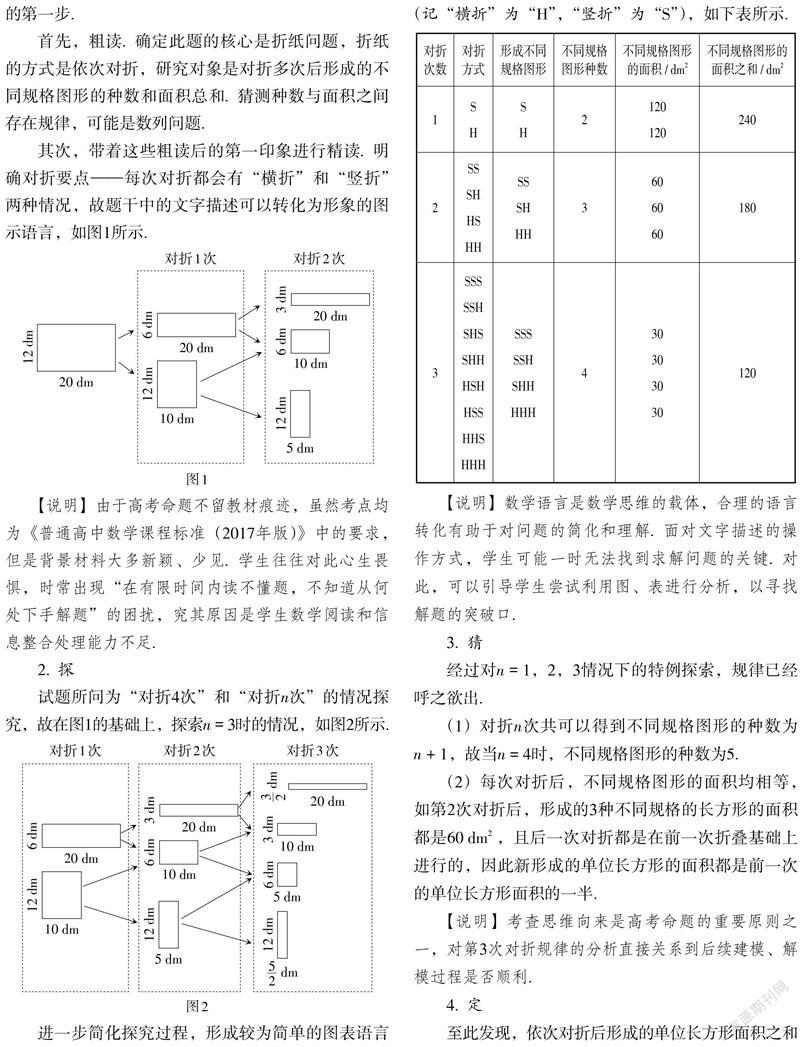
其次，带着这些粗读后的第一印象进行精读. 明确对折要点——每次对折都会有“横折”和“竖折”两种情况，故题干中的文字描述可以转化为形象的图示语言，如图1所示.

【说明】由于高考命题不留教材痕迹，虽然考点均为《普通高中数学课程标准（2017年版）》中的要求，但是背景材料大多新颖、少见. 学生往往对此心生畏惧，时常出现“在有限时间内读不懂题，不知道从何处下手解题”的困扰，究其原因是学生数学阅读和信息整合处理能力不足.

2. 探

试题所问为“对折4次”和“对折n次”的情况探究，故在图1的基础上，探索n = 3时的情况，如图2所示.

进一步简化探究过程，形成较为简单的图表语言（记“横折”为“H”，“竖折”为“S”），如下表所示.

【说明】数学语言是数学思维的载体，合理的语言转化有助于对问题的简化和理解. 面对文字描述的操作方式，学生可能一时无法找到求解问题的关键. 对此，可以引导学生尝试利用图、表进行分析，以寻找解题的突破口.

3. 猜

经过对n = 1，2，3情况下的特例探索，规律已经呼之欲出.

（1）对折n次共可以得到不同规格图形的种数为n + 1，故当n = 4时，不同规格图形的种数为5.

（2）每次对折后，不同规格图形的面积均相等，如第2次对折后，形成的3种不同规格的长方形的面积都是60[dm2]，且后一次对折都是在前一次折叠基础上进行的，因此新形成的单位长方形的面积都是前一次的单位长方形面积的一半.

【说明】考查思维向来是高考命题的重要原则之一，对第3次对折规律的分析直接关系到后续建模、解模过程是否顺利.

4. 定

至此发现，依次对折后形成的单位长方形面积之和是按照一定规律排列的一列数，故确定建立数列模型.

设对折k次，记单位长方形的面积之和为[Sk，] 即依次形成的单位长方形的面积之和为数列[Sk.]

【说明】数学建模是高中数学学科六大核心素养之一，亦是高考常见的考查方向，重在对学生数学思维的穿透力和深刻性的考查. 此题通过特例分析、推理构建数列模型. 在确定通项时，方法1侧重归纳推理，方法2则通过递推关系推导通项，体现了“以生考熟”，鼓励学生通过多种途径进行思维创新，突出了对数学本质的考查.

【说明】解决这一特定数列前n项求和问题体现了回归基础，强调了对通性、通法的考查. 方法1以“列、乘、减”求和，关键在于“错位”相减构造等比数列;方法2将[Tn]分解为一个等比数列和一个与自身相似的数列进行求和，难点在于转化时需要进行“添项”处理. 这两种方法殊途同归，都是考查学生数学运算能力的重要载体.

问题延伸：若将题中长方形纸的规格改为20 dm × 10 dm，情况如何呢？若将题中长方形纸的规格改为a dm × b dm，情况又如何呢？

三、教学启示

一道精彩的高考试题中蕴含着丰富的教育内涵，基于这道数列创新题的命题与解答分析，笔者总结出“两回归，两重视”教学建议.

1. 回归基础，重视通性、通法训练

九层之台，起于累土. 高考历來重视对基础知识和基本技能的考查，注重对通性、通法的研究. 分解此道试题，不难发现所考查的数列概念、等比数列概念、递推数列求通项，以及特殊数列求和等考点均是高中数学中的主干知识或重点知识，无论从内容上还是难度上来看，均属于高考数学中的稳定考查对象. 因此，在高三复习中，要注意回归基础、追根溯源，对于基础知识、基本方法的巩固与提升要做到稳扎稳打，切不可求快、求偏，根深才能叶茂，只有基石稳固，才能求突破、求发展.

2. 回归本质，重视数学学科核心素养生成

在高考命题坚持“信息切入，能力考查”的大背景下，回归数学本质是从命题到教学的强烈呼声. 回顾此道试题，对于数学抽象、逻辑推理、数学建模等素养的综合考查突出了从知识立意到能力立意，再到学科素养立意的评价核心. 因此，在高三复习中，教师要宁心静气、精选精练，敢于留白，敢于利用充足的时间引导学生进行深度思考，并且启发学生抓住数学本质，关注一题多解、多题一解，学会探究、学会思考、学会总结，从而实现数学学科核心素养的生成.

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[2]任子朝，赵轩. 基于高考评价体系的数学科考试内容改革实施路径[J]. 中国考试，2019（12）：27-32.

[3]曾荣，渠东剑. 回归数学本真，关注新颖题型：比较视角下的“八省联考”数学卷特点及教学建议[J]. 教育研究与评论（中学教育教学），2021（2）：37-41.