中国巨灾保险基金规模测算研究

杨 亮,孟生旺,徐婷婷

(1.西南财经大学 金融学院,四川 成都 611130;2.中国人民大学 统计学院,北京 100872;3.西安财经大学 经济学院,陕西 西安 710100)

一、引言

巨灾保险是世界性难题,中国巨灾保险虽历经多年探索与实践但仍发展缓慢。近年来,自然灾害频发,一次次为我们敲响警钟:面对灾害,我们缺乏的不仅仅是减灾救灾的自然科学知识,更缺乏防灾减损的经济学意识尤其是巨灾保险意识。以“5.12”汶川特大地震为例:地震造成直接经济损失8 500亿元,但保险赔偿金额仅20亿元,占比约0.25%。据瑞士再保险的统计,2015年全球保险理赔占自然灾害损失的平均比例是35%,发达国家这一比例甚至超过80%。这意味着中国保险的社会治理职能尤其是防灾减损职能未充分发挥,巨灾保险职能缺位问题突显。近年来,中共中央和各部委多次出台决定或意见,落实推动中国巨灾保险制度的建立与完善:2013年《中共中央关于全面深化改革若干重大问题的决定》明确提出“完善保险经济补偿机制,建立巨灾保险制度”;2014年《国务院关于加快发展现代保险服务业的若干意见》(保险业“新国十条”)中提出“建立巨灾保险制度。研究建立巨灾保险基金、巨灾再保险等制度,逐步形成财政支持下的多层次巨灾风险分散机制”;2016年《中国保险业发展“十三五”规划纲要》中提出“研究建立地震巨灾保险基金,研究建立覆盖洪水、台风等多灾因巨灾保险制度”;2016年《建立城乡居民住宅地震巨灾保险制度实施方案》中提出建立“地震巨灾保险专项准备金”。目前,中国已逐步建立起了以党中央为主导、以地方政府为支撑的多层次巨灾风险分散机制。各级政府以地震巨灾保险为契机,积极推动中国巨灾保险体系构建,相继开展了省级财政支持的巨灾保险试点。如四川省住宅地震巨灾保险试点、云南省政策性地震指数保险等。

巨灾保险基金是巨灾风险管理体系的核心与基础。将传统的中央政府灾害救济基金转变为巨灾保险基金,可以缓解财政压力,提高灾害救济效率[1]。巨灾保险基金的核心问题是基金规模测算[2-3]。研究如何改进中国巨灾保险基金规模测算方法,提高基金规模测算精度,更好地发挥巨灾保险的风险分散及损失补偿作用,具有重要的理论与现实意义。

二、文献综述

中国对建立巨灾保险基金的探讨始于20世纪80年代,工作核心是建立巨灾保险基金的必要性及其筹资模式、运营机制等问题。受到精算技术、巨灾保险意识、国民经济和社会发展等现实条件的制约,早期对巨灾保险及巨灾保险基金的研究主要集中于巨灾保险制度构建、多层次巨灾保险体系构建、巨灾风险分散机制以及巨灾保险产品定价等方面[4-7]。2008年后,由于“5·12”汶川特大地震给国民经济带来了巨大损失,巨灾保险尤其是地震巨灾保险得到了充分重视,学界对建立巨灾保险基金的探讨不断深入,总结起来,主要包括三个方面。(1)巨灾保险基金在巨灾保险制度中的作用和地位。巨灾风险具有可保性,对其进行保费补贴、再保险以及通过资本市场和公共部门进行融资有助于扩大巨灾风险的可保性[2,8]。建立巨灾保险基金无疑是扩大巨灾风险可保性的有效方法之一。(2)巨灾保险基金的运作模式研究。中国巨灾保险基金的运作,是政府主导与市场辅助相结合的模式。其中,巨灾证券化研究是巨灾保险基金运作模式的新动向[9]。(3)巨灾保险基金规模测算。对巨灾保险基金规模进行测算是巨灾保险基金研究的核心问题,如地震巨灾保险基金规模的测算研究等[2-3,10]。

保险基金规模的测算是巨灾保险体系构建的重要环节,也是学界研究的热点和重点问题。按照保障范围的不同,巨灾保险基金可以被划分为专项巨灾保险基金和综合性巨灾保险基金两类。对于专项巨灾风险基金规模测算的研究文献有:采用VaR方法对中国地震保险基金规模进行测算,结果表明:地震保险基金规模与风险容忍度和再保险附加费率相关,基金规模从8.56亿元到216亿元不等[10];采用CVaR方法再次对中国地震巨灾保险基金规模进行测算,结果表明:基于CVaR方法测算的基金规模高于VaR方法下的基金规模,且CVaR对超大规模的地震损失更敏感[11];探讨Mixed Erlang-Pareto组合分布在VaR、TVaR和地震巨灾保险定价等方面的具体应用,对中国1990—2018年4.5级以上地震所造成的直接经济损失数据进行组合分布建模[12];注重巨灾损失后尾特征的研究,研究发现:在偿付能力为0.99水平下,地震死亡保险基金规模为77亿元至206亿元不等[3]。综合性巨灾保险基金通过对所有的巨灾风险建立一个基金,并按照一定规则进行统一测算。譬如,以地震和洪水两种巨灾为研究对象,发现在相同风险容忍度下,联合巨灾保险基金的规模不大于分别建立巨灾保险基金的规模之和[2]。

国外对巨灾保险基金规模的测算,主要集中于最大承保能力的研究,譬如,以市场容量和破产理论为基础,基于大数法则测算保险公司的承保能力[13]。建立最优分保比例模型,提出当每一个再保险人持有的风险与其市场占有率相对应时,再保险市场风险配置将达到均衡状态[14]。结合期货合约和衍生工具的估值理论,并将其应用于巨灾保险领域,采用Markov模型对巨灾保险进行定价[15]。在赔付支出最大化和赔付不足最小化的限制条件下构建函数,进行数学推导并测算巨灾保险基金规模[16]。以美国的192起巨灾损失为研究对象,发现其中75%的巨灾发生后会产生“需求激增”效应,因此保险人在对巨灾保险进行定价时应当考虑风险溢价和经济成本[17]。计算美国巨灾超赔再保险价格,研究表明:在巨灾损失服从对数正态分布条件下,起赔点为250亿美元、保额为500亿美元的超赔再保险价格为3.7亿美元;若巨灾保险基金的作用是提供再保险,则每年需要筹集3.7亿美元的资金以应对巨灾风险损失[18]。

巨灾保险基金规模的测算结果与使用的风险度量工具和保费准则密切相关,在不同的风险度量工具或保费准则下探讨最优再保险策略的文献可以参考Chi等人的研究[19-21]。巨灾保险基金规模是指在一定的风险容忍度下,能够维持巨灾保险市场稳定运行且能覆盖巨灾损失赔偿的最小基金规模。现有文献将巨灾保险基金定位于再保险性质,根据优化目标的不同,选择VaR、CVaR等指标作为风险度量工具,考虑不同的再保险策略,实现对巨灾保险基金规模的测算。现有文献大多只讨论了再保险策略的选择问题,忽略了保费准则在基金测算过程中的作用,比如保费函数中参数的人为设定问题,使得测算结果可能存在偏差。为此,本文同时考虑再保险策略和保费准则的影响,在风险度量最小化目标下寻找最优分保函数,进一步提高基金规模的测算精度。

本文的主要贡献如下:第一,突破单一再保险策略的限制,在广义再保险策略下,探讨最优再保险策略的求解问题,在全局最优意义下选择最优再保险策略;第二,克服人为设定保费准则参数的弊端,基于再保险费最小化目标实现对保费准则参数的求解,为进一步的巨灾保险基金规模测算奠定基础;第三,给出经验期及未来年份巨灾保险基金规模理论表达式,并基于1980—2020年中国自然灾害巨灾损失数据进行实证研究,验证了理论结果的合理性;第四,基于该基金规模的测算结果,进一步探究保险公司的风险容忍度对再保险价格以及分出额函数的影响,为保险公司在风险转移过程中选择最优再保策略提供理论支撑。

三、扭曲测度下的最优再保险策略

再保险也称“分保”,是原保险人在原保险合同的基础上,通过签订分保合同,将其承保的部分风险和责任转移给其他保险公司的行为。再保险通过将风险控制在一定范围内的同时,寻找损失赔付额和再保险费之间的平衡点,实现公司经营目标的最大化。

(一)保费准则与再保险策略

在购买再保险时,需要根据一定的准则计算再保险保费,该准则即为保费准则。设Y为原保险人承保的巨灾责任风险;f(x)为分出额函数,即原保险人转移给再保险人的风险;If(x)为原保险人自留风险额函数,则:

If(Y)=Y-f(Y)

(1)

此时,巨灾保险的再保险费可以表示为:

(2)

其中,r(x|θ)为在给定参数θ条件下的保费函数,是一个有界的左连续增函数,且满足r(0|θ)=0以及r(x|θ)>0,x>0[22]。再保险费是原保险人向再保险人转移风险时缴纳的成本。常见的保费准则及其函数形式如表1所示。基于式(1)与式(2),原保险公司的总支出可以表示为自留损失和再保险费之和:

表1 常见的保费准则

Tf(Y)=If(Y)+ur[f(Y)|θ]

(3)

再保险通过对分出额函数f(x)设置不同的限制,形成不同的再保险策略。在一定限制条件下,确定分出额函数f(x)的方法就是再保险策略。譬如,成数再保险策略就是通过合同约定的比例确定分出额和自留额,并按照该比例分配保费、摊付赔款。表2为常见的再保险策略及其函数形式。

表2 常见的再保险策略

(二)扭曲风险度量

扭曲概率从最早思想的提出,到随后首次将扭曲概率应用于保险精算领域,通过定义扭曲函数改变原有的概率分布,并采用变换后的概率分布来度量风险,这种方法称作扭曲风险度量(Distortion Risk Measure)方法[23-24]。对于非负的损失随机变量X,扭曲风险度量的一般表达式如下:

(4)

在式(4)中,g(x)为扭曲函数,是定义在[0,1]上且满足g(0)=0和g(1)=1的增函数;S(x)=Pr(X>x),为随机变量X的生存函数。

表3是常见扭曲风险度量及其对应的扭曲函数。可以证明,在式(4)中,当且仅当扭曲函数g(x)为凹函数时,即g′(x)≥0且g″(x)≤0,扭曲风险度量ρg(X)具有次可加性。

表3 常见的扭曲风险度量及其扭曲函数

对于非负随机变量X,经过扭曲变换之后的随机变量记为X*,则有如下关系:

fX*(x)=g′[1-FX(x)]fX(x)

(5)

式(5)表明,经过扭曲变换之后的随机变量X*的密度函数,是在原有随机变量X密度函数基础上进行了加权变换,由于g′[1-FX(x)]关于x为单调递增函数,使得扭曲变换后的随机变量X*的右尾被赋予了较大的权重。该特征能较好地捕捉巨灾损失分布所包含的信息,因此在巨灾风险度量方面具有广阔的应用空间。

(三)无保费约束时的最优再保险策略

在再保险实务中,根据是否对再保险费进行限制,再保险问题可以分为有保费约束的最优再保险和无保费约束的最优再保险。本文只讨论无约束的最优再保险策略问题。为了有效地避免道德风险,假设分出额函数f(x)和自留函数If(x)均为单调递增函数,即原保险人的自留额If(x)与再保险人的承保额f(x)都随着实际损失X的增大而增加。因此,对于式(3)中原保险人的总赔付额Tf(x),在扭曲风险度量ρg(x)下,无保费约束的最优再保险问题可以表示为:

(6)

其中,F为f(x)的可行函数域,F中所有的f(x)均满足0≤f(x)≤x,且f(x)与If(x)都是单调增函数。根据已有研究结果[22],式(6)可以进一步表示为:

(7)

其中,SX(t)=Pr(X>t)表示随机变量X的生存函数;r(x)为式(2)中的保费函数;g(x)为式(4)中的扭曲函数。在原保险人的风险度量值最小化的条件下,根据式(7)可求出最优分出额函数f*(x)。

(四)求解保费准则参数

原保险人将风险转移给再保险人时,需要缴纳一定数额的再保险费。在原保险人承担的风险最小化的条件下,为使得原保险人缴纳的再保险费达到最低,应满足如下方程组:

(8)

其中,θ为参数θ的可行域。利用方程(8)求解保费函数r(x|θ)中的参数θ,摆脱人为给定保费准则的主观影响,提高再保险费的准确性,从而为巨灾保险基金规模测算奠定基础。

(9)

这里,不妨假设巨灾损失X服从对数正态分布,其分布函数可以表示为:

其中,μ和σ分别为对数正态分布的位置和尺度参数。令

则有:

故有:

(10)

将式(10)中的α替换为1/(1+β),可得:

(11)

将式(10)、(11)带入到式(9),可得:

(12)

其中,

将式(12)带入到方程(8),则有:

(13)

方程(13)中,分位数水平α可根据原保险人对风险的厌恶程度来选择。根据方程(13),应用数值算法求得保险费准则参数β。将参数α和β,以及式(12)带入式(3),即可得到在最优再保险策略下保险公司的总赔付额,即:

(14)

(五)巨灾保险基金规模测算

巨灾保险基金规模是指在可接受的风险控制范围内,能够维持巨灾保险市场正常运行所需的最小规模的损失赔偿金额。由式(7)可以求出最优分出额函数f*(x),使得原保险人承担的风险最小;将最优分出额函数f*(x)带入式(4)可得巨灾保险基金规模(Scale of the Catastrophe Insurance Fund,SCIF)为[2]:

(15)

以下考虑VaR风险度量和期望保费准则,基于最优分出额函数式(7),分别采用精算中的个体风险模型(Individual Risk Model)和聚合风险模型(Collective Risk Model),测算经验期巨灾保险基金的总规模,以及未来各个年份巨灾保险基金的年规模。

在经验期,假设第i次灾害的损失金额为随机变量Zi,各个巨灾损失之间相互独立。在给定风险度量方法、保费准则以及最优再保险策略条件下,进一步假设保险公司对每次巨灾的总赔付金额相互独立,则保险公司在经验期的巨灾赔付金额可以表示为:

(16)

将式(16)带入式(15),则基于VaR风险度量条件下经验期的巨灾风险PMLα可表示为:

(17)

式(17)中,n表示经验期内灾害的总次数;q为分位数水平,表示对风险的容忍最高限度,即实际损失超过巨灾保险基金的概率不会超过q。q与α类似,两者均表示对风险的容忍程度。与α不同的是,q是原保险人对所有业务线的总风险控制水平,α则是原保险人对单个业务线的风险控制水平。为了区别q与α之间整体和部分的关系,这里我们将q表述为风险阈值,α为风险容忍度。

将未来某一年的巨灾保险基金规模视为一个整体,Zi表示该年份发生的第i次巨灾损失额,N表示该年份发生的巨灾总次数。假设Zi、N均为随机变量,Z1,Z2,…,ZN之间独立同分布,且独立于随机变量N。在给定风险度量工具、保费准则以及最优再保险策略条件下,进一步假设保险公司对每次巨灾的赔付金额相互独立,则未来某一年份的巨灾损失额可以表示为:

(18)

类比式(17),基于VaR风险度量,可得到未来一个年份的巨灾风险PMLα:

(19)

其中,

C·[1-F(A+C)]

最终,将式(17)与(19)带入式(15),可得到经验期和未来某一年的巨灾保险基金规模。

四、实证研究

本文数据来源于紧急灾难数据库(Emergency Events Database,EM-DAT),该数据库于1988年由世界卫生组织与比利时灾后流行病灾害研究中心(Centre for Research on the Epidemiology of Disasters,CRED)共同创建,是全球范围内灾害数据权威数据库之一。EM-DAT灾害数据库可以查询到1900年至今的已发生灾害数据,考虑到数据库1980年之前数据质量不高的问题,最终选取了中国1980—2020年发生的自然灾害损失数据进行建模,计算无保费约束条件下的最优再保险策略,同时测算巨灾保险基金的规模。这里,自然灾害类型及其包括的具体类型详见EM-DAT数据库。

(一)数据描述

中国1980—2020年期间发生且有损失记录的自然灾害总共548起。为了让数据更具有可比性且兼具巨灾损失的特点,本文对数据进行了如下预处理。首先,根据灾害发生年份美元对人民币汇率,将损失金额统一折算成以人民币为单位;其次,考虑到不同年份通货膨胀的影响,利用灾害发生年份当年的CPI指数,将损失金额统一折算成以2020年为对比基期的购买力;最后,考虑到巨灾破坏力强的特点,选取折算后损失金额大于等于1 000万元人民币的自然灾害记录,总计530条,其最大值、最小值、均值、标准差、偏度以及峰度分别为:71 530.01、1.06、978.88、4 081.68、12.10以及183.63,损失金额的计量单位为千万元。

图1是根据530条损失金额数据及其对数变换绘制的直方图与经验密度函数,可以看出,巨灾损失金额数据具有典型的尖峰厚尾特征,但经过对数变换以后,损失金额的经验密度函数呈现出对称的“钟形”结构,因此可以初步判断这组巨灾损失数据适合用对数正态分布进行描述。

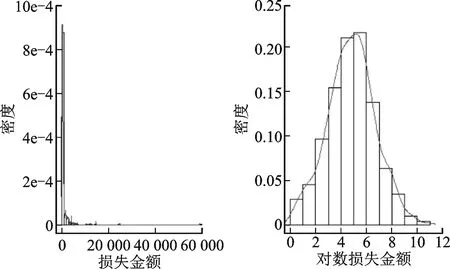
图1 损失金额及其对数变换的直方图与经验密度函数

(二)巨灾损失分布的拟合

应用各种常见的损失分布模型对前述巨灾损失数据进行拟合,结果如表4所示。其中,对数正态分布的偏差、AIC和BIC统计量都小于其他分布模型,说明对数正态分布模型的拟合效果最好,这个结论与图1吻合。

表4 巨灾损失金额数据的拟合结果比较

图2 对数正态分布拟合的残差

(三)巨灾保险基金规模测算

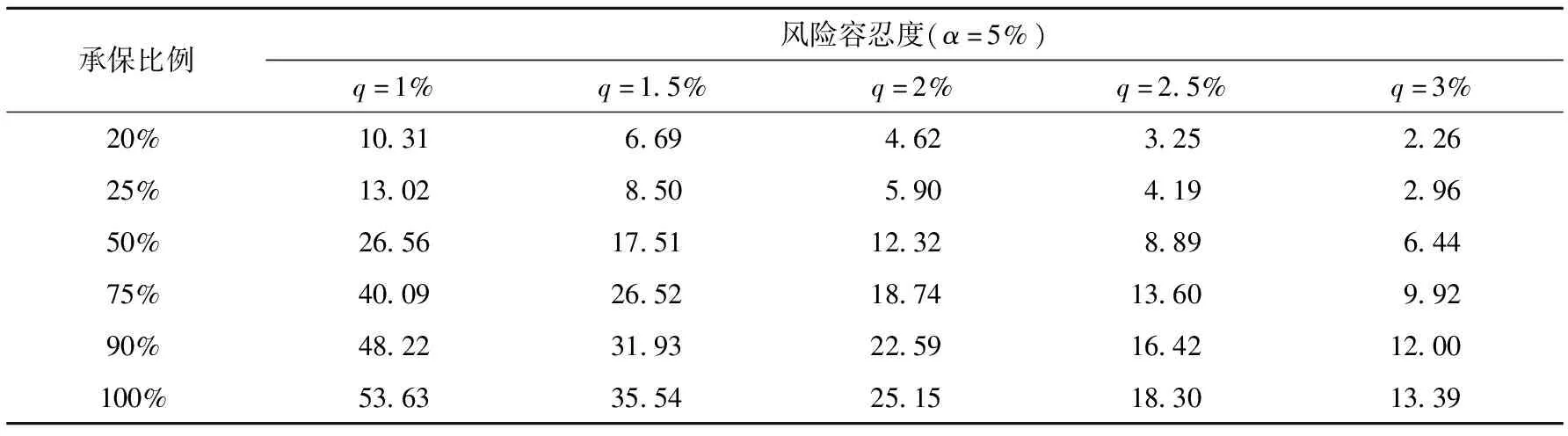
表5 不同承保比例及风险容忍度下经验期巨灾保险基金的总规模 单位:万亿元

为了实现对未来某年份巨灾发生次数的预测,对式(19)中随机变量N建立泊松回归模型,并引入三次样条对巨灾发生年份变量进行平滑处理。泊松回归模型结果表明,随着时间推移未来几年巨灾发生次数存在下降趋势。表6给出了不同承保比例条件下2021—2025年各年份的基金规模。譬如,当风险容忍度为5%、巨灾保险的承保比例为20%时,2021年中国巨灾保险基金规模为0.012万亿元。表6结果表明,相同年份条件下随着风险容忍度的增大,巨灾保险基金的规模会逐渐减小;相同承保比例条件下随着时间推移未来几年巨灾保险基金规模存在下降趋势。

表6 不同承保比例及固定风险容忍度下未来五年巨灾保险基金规模 单位:万亿元

表7给出了不同承保比例及风险容忍度下2021年巨灾保险基金的规模。结果表明,随着承保比例的增大和风险容忍度的减小,2021年巨灾保险基金的总规模不断扩大。

表7 不同承保比例及风险容忍度下2021年巨灾保险基金的规模 单位:万亿元

五、进一步讨论:风险容忍度的影响

(一)风险容忍度对分出额函数的影响

图3 分出额函数的变化趋势

(20)

(二)风险容忍度对附加保费因子的影响

图4为式(13)中再保险费最小时,原保险人风险容忍度α与再保险定价过程中的风险附加因子β之间的关系,即图4中的实线部分。可以看出,风险附加因子β随着风险容忍度α的增加先增后减。以α与β分别为横坐标和纵坐标,以β=1/α-1为分界线,可以将第一象限划分为两个区域,分界线右上侧的点使得分出额函数中C的取值为0(图4中灰色区域),此时分出额为0,即原保险人停止再保险行为;同理,在分界线左下侧(图4中非灰色区域),表示原保险人会选择再保险行为。

图4 风险容忍度对附加保费因子的影响

综上所述,图4中实线右侧递减部分落在灰色区域内,该部分曲线上的点没有发生实际再保险行为;曲线的左侧递增部分,一方面满足了再保险费的最小化,同时原保险人也实际发生了再保险行为。

(三)风险容忍度对再保险费的影响

风险容忍度α是再保险费的重要影响因素。从图5可看出,随着原保险人实际风险容忍度的提高,其所能接受缴纳的总再保险费金额在逐渐下降,随着风险容忍度的不断提高该下降速度在逐渐加快,当到达某个临界值时,原保险人最终选择终止所有再保险行为,此时总再保险费为零。

图5 风险容忍度与再保险费之间的关系

六、结论与展望

基于风险度量和再保险定价准则,本文构建了一般意义下的最优再保险策略,可以在一定程度上提高巨灾保险基金规模测算的精度。通过理论推导与实证研究,得出如下结论:

第一,在放宽再保险策略的常规性限制以及对保费准则的约束后,可以避免以往研究中人为设定参数的弊端,防止最优再保险陷入“局部最优”之中,从而可以实现全局最优下的再保险策略选择。

第二,以中国1980—2020年间的灾害损失数据为例,采用VaR—期望保费原理得出中国巨灾保险的最优再保险策略为有上限的止损策略。

第三,将巨灾保险基金视为再保险性质,基于不同的风险容忍度和承保比例,测算了中国巨灾保险所需的基金规模。

最后,深入探讨了风险容忍度对分出额函数、附加保费因子和再保险费的影响。

最优再保险策略的选择和巨灾保险基金规模的测算具有重要的理论和现实意义,在实际应用中会受到各种因素的影响,譬如,在未来的研究中,有必要进一步考虑自然灾害类型之间的差异性、相依关系以及风险分散作用。