怎一个“轻质”了得

■河北省石家庄市河北正定中学 杨高轩

理想化模型是一种为了便于研究问题而建立的高度抽象的理想客体,其中把研究对象所处的外部条件理想化而建立的模型叫条件模型,比如轻质圆环、轻质绳、轻质杆、轻质丝绸、轻质薄板、轻质弹簧、轻质滑轮等。“轻质”的意思是研究对象的质量可以忽略不计,但在不同的环境中,“轻质”又有着不同的含义,下面就“轻质”在力的观点、能量观点、动量观点三大力学体系中的含义进行分析,供同学们参考。

一、“轻质”在力的观点中的含义

1.不计物体的重力。

物体的质量忽略不计,根据G=mg可知,物体的重力可以忽略不计。不计物体的重力多见于物体受力平衡的情景中。

例1如图1所示,光滑细杆固定在竖直面内,细杆与水平面之间的夹角θ=60°,细杆上套有一轻质小圆环。在一根轻质弹性绳AB的中点处做一记号O,把弹性绳A端与小圆环相连,在B端挂上一质量为m的小物块,在O点系上一根刚性细线,细线另一端固定在竖直墙壁上,系统稳定后,细线恰好水平,OB段长为l。弹性绳的弹力遵从胡克定律,其形变在弹性限度内,重力加速度为g。则( )。

图1

A.AO段长为l

B.AO段长为2l

C.AO段的弹力等于OB段的弹力

D.AO段的弹力比OB段的弹力大mg

分析:小圆环是轻质的,不计重力;细杆是光滑的,对小圆环没有摩擦力。根据平衡条件可知,轻质弹性绳AO段与细杆垂直,与水平面之间的夹角为30°。弹性绳和细线也是轻质的,重力不计,选O点为研究对象进行受力分析时不需考虑它们的重力。

解:选O点为研究对象,设弹性绳AO段的弹力为F1,弹性绳OB段的弹力为F2,根据平衡条件得F2=mg,F1sin 30°=F2,解得F1=2F2=2mg,因此AO段的弹力比OB段的弹力大mg,选项C 错误,D 正确。设弹性绳的劲度系数为k,原长为2l0,AO段长为la,根据胡克定律得F1=k(la-l0),F2=k(l-l0),因此l＜la＜2l,选项A、B错误。

答案:D

2.物体受到的合外力为0。

物体的质量忽略不计,根据F=ma可知,无论物体的加速度为多大,它受到的合外力均为0。如图2所示,轻质弹簧放置在水平面上,左端拴接一小物块,在弹簧右端施加大小为F的拉力使物块在水平面上运动,无论物块在水平面上做匀速直线运动还是加速运动,无论物块的加速度怎么变化,轻质弹簧所受合外力均为0,物块对弹簧的拉力都等于F;以任意一段弹簧为研究对象,其受到的合外力也为0,因此弹簧中弹力处处相等,均等于F。

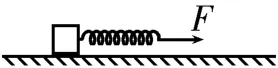
图2

例2如图3所示,底角为α的等腰三角形斜面体固定在水平面上,一足够长的轻质绸带跨过斜面体的顶端铺放在两侧斜面上,绸带与斜面之间无摩擦。现将质量分别为M、m(M＞m)的小物块同时轻放在两侧斜面的绸带上。两物块与绸带之间的动摩擦因数相等,且最大静摩擦力等于滑动摩擦力。在α角取不同值的情况下,下列说法中正确的是( )。

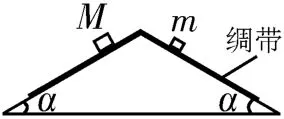
图3

A.两物块所受摩擦力的大小总是相等

B.两物块不可能同时相对绸带静止

C.质量为M的物块不可能相对绸带发生滑动

D.质量为m的物块不可能相对斜面向上滑动

分析:轻质绸带的质量不计,受到的合外力为0,轻质绸带与斜面之间无摩擦,受到两个物块对它的摩擦力总是等大反向的。

解:选轻质绸带为研究对象,设两个物块对绸带的摩擦力分别为fM、fm,根据牛顿第二定律得fM-fm=m绸a=0,即fM=fm。质量为M的物块对绸带的摩擦力和绸带对质量为M的物块的摩擦力、质量为m的物块对绸带的摩擦力和绸带对质量为m的物块的摩擦力是两对相互作用力,根据牛顿第三定律可知,两物块受到绸带的摩擦力总是大小相等,选项A 正确。设两物块与绸带之间的动摩擦因数为μ,当α较小,Mgsinα＜μMgcosα,mgsinα＜μmgcosα时,质量为M的物块加速下滑,质量为m的物块加速上滑,均相对绸带静止,选项B、D 错误。因为M＞m,所以质量为M的物块与绸带之间的最大静摩擦力较大,绸带与质量为M的物块始终相对静止,质量为m的物块可能相对绸带滑动,选项C正确。

答案:AC

例3如图4所示,一足够长轻质薄硬纸板置于光滑水平地面上,纸板上放有质量mA=mB=1 kg的A、B两物块,A、B两物块与纸板之间的动摩擦因数分别为μ1=0.3,μ2=0.2。水平恒力F作用在物块A上,假设最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2。则( )。

图4

A.若F=1 N,则两物块和纸板都静止不动

B.若F=1.5 N,则物块A所受摩擦力大小为1.5 N

C.若F=8 N,则物块B的加速度为4 m/s2

D.无论力F多大,物块A与纸板都不会发生相对滑动

分析:薄硬纸板是轻质的,受到的合外力总是0,因此它受到A、B两物块的摩擦力总是等大反向的。

解:物块A与纸板之间的最大静摩擦力fAmax=μmAg=3 N,物块B与纸板之间的最大静摩擦力fBmax=μmBg=2 N。若F=1 N,即F＜fAmax,则两物块与纸板保持相对静止,整体向左做匀加速运动,选项A 错误。若F=1.5 N,即F＜fAmax,则两物块与纸板保持相对静止,整体向左做匀加速运动,根据牛顿第二定律得F-f=mAa,因此物块A受到的摩擦力f＜F,即f＜1.5 N,选项B错误。当物块B刚要相对纸板滑动时,物块B受到的静摩擦力达到最大值,根据牛顿第二定律得fBmax=mBa0,又有fBmax=2 N,解得a0=2 m/s2;对由两物块和纸板组成的整体应用牛顿第二定律得F0=(mA+mB)a0,解得F0=4 N,即当拉力F达到4 N 时,物块B恰好相对纸板运动,此时物块B受到的摩擦力f=2 N;纸板受到物块A对它的最大静摩擦力大于物块B对它的最大静摩擦力,因此物块A和纸板之间不会发生相对运动;继续增大拉力F的值,不会改变物块B的受力情况,物块A受到的摩擦力总是等于2 N,不会相对纸板滑动,选项D 正确。若F=8 N,则物块B与纸板之间的摩擦力为滑动摩擦力,加速度为2 m/s2,选项C错误。

答案:D

二、“轻质”在能量观点中的含义

1.不计物体的动能及其变化量。

例4如图5所示,粗糙程度处处相同的水平桌面上有一长度为L的轻质细杆,一端可绕竖直光滑轴O转动,另一端与质量为m的小木块相连。木块以水平初速度v0出发,恰好能完成一个完整的圆周运动。在运动过程中,木块所受摩擦力的大小为( )。

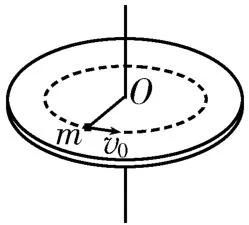
图5

分析:轻质细杆的质量为0,绕竖直光滑轴O转动,因此细杆对木块的弹力沿细杆方向,对木块不做功;细杆的动能及其动能变化量忽略不计,因此木块受到桌面的摩擦力对木块做的功等于木块的动能变化量。

解:木块受到桌面的摩擦力总是与木块的运动方向相反,根据动能定理得-f·2πL=,解得

答案:B

2.不计物体的重力势能及其变化量。

物体的质量忽略不计,根据Ep=mgh可知,物体的重力势能及其变化量可以忽略不计。

例5如图6所示,一根轻质弹簧的劲度系数k=100 N/m,其下端固定在倾角θ=37°的光滑斜面底端,上端连接物块P。轻绳跨过定滑轮O,一端与物块P相连,另一端与套在光滑水平直杆上的物块Q相连,定滑轮到水平直杆的距离d=0.4 m。初始状态下,在外力作用下,物块Q静止在A点不动,轻绳与水平直杆之间的夹角α=30°,轻绳的张力大小T=45 N。现将物块Q由静止释放,物块Q向左运动经过B点时,轻绳与水平直杆之间的夹角β=53°。已知物块Q的质量m1=0.2 kg,物块P的质量m2=5 kg,不计滑轮大小及摩擦,取重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8。求:

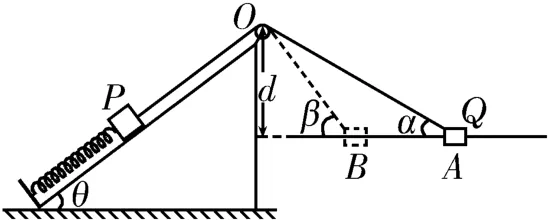
图6

(1)物块P静止时,弹簧的伸长量x0。

(2)物块Q运动到B点时的速率vB。

(3)在物块Q由A点运动到B点的过程中,轻绳拉力对它做的功W。

分析:定滑轮的质量不计,不考虑其转动动能;弹簧的质量不计,在物块P向下运动的过程中,弹簧的重力势能及其变化量不计,由物块P和Q组成的系统的机械能守恒。

解:(1)物块P静止时,根据平衡条件得T=m2gsinθ+kx0,解得x0=0.15 m。

(2)将物块Q由静止释放,物块P沿斜面下滑的距离,弹簧的压缩量Δx=x-x0=0.15 m。因为Δx=x0,所以物块Q运动到B点时,弹簧的弹性势能与物块Q在A点时的相等,即在物块Q由A点运动到B点的过程中,弹簧的弹力对物块P做的功为0。在物块P下滑的过程中,由物块P和Q组成的系统的机械能守恒,则又有vP=vBcosβ,解得vB=3 m/s。

(3)在物块Q由A点运动到B点的过程中,对物块Q应用动能定理得解得W=0.9 J。

三、“轻质”在动量观点中的含义

物体的质量忽略不计,根据p=mv可知,物体的动量及其变化量可以忽略不计。

例6如图7所示,光滑水平横杆AB上固定有一个阻挡钉C,横杆上套一轻质圆环,圆环上系一长度为L、足够牢固、不可伸长的轻质细绳,细绳的另一端拴一质量为m的小球。现将圆环拉至阻挡钉C左侧处并将细绳拉直,让细绳与横杆平行,由静止同时释放圆环和小球。已知重力加速度为g,则关于之后的运动情况,下列描述正确的是( )。

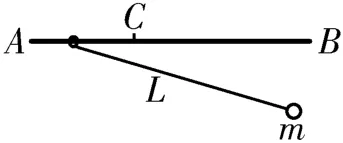
图7

A.小球不可以回到横杆所在的高度

B.小球运动到最低点时的速度小于 2gL

C.小球到达最低点之前一直做曲线运动

D.小球运动到最低点时对细绳的拉力小于3mg

分析:圆环运动到阻挡钉C所在位置的过程中,由圆环和小球组成的系统在水平方向上的动量守恒;圆环的质量不计,则小球的水平分动量为0,水平分速度为0,只有竖直方向的分速度,做自由落体运动。

解:圆环运动到阻挡钉C所在位置的过程中,小球做自由落体运动,当圆环与阻挡钉C碰撞后,小球绕阻挡钉C做圆周运动,选项C错误。设圆环与阻挡钉C碰撞时,细绳与水平方向之间的夹角为θ,碰撞前瞬间小球的速度为v,根据几何关系得,根据机械能守恒定律得,解得(即θ=37°),v=圆环与阻挡钉C碰撞后瞬间,小球的速度v＇=vcosθ,即细绳绷直瞬间,小球沿细绳方向的分速度突变为0,有能量损失,因此小球不能回到横杆所在的高度,选项A 正确。在小球由静止释放至运动到最低点的过程中,若没有能量损失,设小球运动到最低点时的速度为v0,根据机械能守恒定律得mgL=,解得因为细绳绷直瞬间有能量损失,所以小球运动到最低点时的速度小于,选项B 正确。设小球运动到最低点时受到的细绳拉力为T,若小球运动到最低点时的速度等于,则根据牛顿第二定律得T-mg=,解得T=3mg。因为小球运动到最低点时的速度小于,所以小球受到的细绳拉力小于3mg。根据牛顿第三定律可知,小球对细绳的拉力小于3mg,选项D 正确。

答案:ABD

综上所述,“轻质”可以引申为不计物体的重力、物体受到的合外力为0、不计物体的动能及其变化量、不计物体的重力势能及其变化量、不计物体的动量及其变化量等,我们对“轻质”的理解要根据具体的情境加以揣摩,做到举“轻”若“重”。