响应面法优化重金属絮凝剂MAMPAM除Cu(Ⅱ)的絮凝条件

杨丽娟，王 刚，张 航，蒋煜峰，杨 凯

兰州交通大学环境与市政工程学院，甘肃 兰州 730070

随着经济、技术的发展，生产生活中产生了大量重金属废水，其中含Cu(Ⅱ)废水主要来源于电镀、矿山开采、印刷电路板、印染等[1]. 微量的Cu(Ⅱ)可促进人体内血红素的合成和铁的吸收，但过量摄入Cu(Ⅱ)会对人体产生不利影响[2-3]. 目前，常用的Cu(Ⅱ)处理方法主要包括化学沉淀法、膜过滤法、混凝-絮凝法、吸附法、电解回收法、电絮凝-离子交换-生化法、铁碳微电解、芬顿工艺等[4-7]，其中絮凝法以其去除率较高、操作方法简便而备受关注. 聚丙烯酰胺(PAM)及其衍生物是水处理中常见的有机高分子絮凝剂，通常被用于去除废水中的色度、浊度、藻类等污染物[8-9]，在重金属废水的处理中，PAM本身不能有效去除溶解态的重金属离子，通常被当作助凝剂使用[10].常青[11]研究发现将重金属的强配位基团接枝到PAM分子链上，能赋予PAM捕集重金属的能力. 例如，袁海飞等[12]将二硫代羧基接枝到PAM上获得了二硫代羧基化磺甲基聚丙烯酰胺(DTSPAM)，对Cu(Ⅱ)的最高去除率达97.49%；李嘉等[13]将巯基接枝到PAM上制备出巯基乙酰化磺甲基聚丙烯酰胺(MASPAM)，对Cu(Ⅱ)的最高去除率达94.7%.

在以往絮凝剂去除重金属性能的研究中，大多集中在采用单因素法考察每个影响因素的单一作用，而未对各影响因素的条件进行优化，也未考察因素之间的交互作用. 响应面法(RSM)是一种综合利用试验设计、统计和数学技术构建模型的方法，不仅可以减少试验次数，而且通过响应面模型和等高线图获得各因素之间的交互作用和最优值[14-15]，因此在各行业取得了广泛应用[16-19]. 目前在絮凝沉淀法方面，响应面法主要应用在絮凝剂制备过程中所需原料的用量及反应条件的优化[20-22]，但对于絮凝条件的优化研究还较少. 该文以聚丙烯酰胺、巯基乙酸等为原料制备出具有重金属螯合能力的絮凝剂巯基乙酰化羟甲基聚丙烯酰胺(MAMPAM)[20]，然后以水样的初始pH、Cu(Ⅱ)初始浓度、MAMPAM投加量/Cu(Ⅱ)初始浓度为3个主要影响因素，以Cu(Ⅱ)去除率为响应值，利用响应面法中的Central Composite Design (CCD)原理设计三因素五水平试验，通过建立响应面模型得到MAMPAM除Cu(Ⅱ)的最优絮凝条件和各因素之间的交互作用，以期为MAMPAM处理含Cu(Ⅱ)废水提供试验参数.

1 材料与方法

1.1 主要仪器与试剂

仪器：JB-2型恒温磁力搅拌器(上海雷磁新泾仪器有限公司)；TA6-1型程控混凝试验搅拌仪(武汉恒岭科技有限公司)；220FS型原子吸收分光光度计(美国瓦里安公司)；Orion828型pH测试仪(美国奥立龙公司).

试剂：聚丙烯酰胺(试验室自制，粘均分子量为24×104)、氯化铜(CuCl2·2H2O，分析纯)、巯基乙酸(HSCH2COOH，分析纯)、氢氧化钠(NaOH，分析纯)、甲醛(HCHO，分析纯)、盐酸(HCl，分析纯).

1.2 MAMPAM的制备

首先将丙烯酰胺、甲酸钠、过硫酸铵溶于蒸馏水中，置于恒温磁力搅拌器上，调节水浴温度为85 ℃反应2 h，制得PAM；然后将PAM稀释为2.00%的水溶液，并按照HCHO与PAM物质的量之比1∶1加入甲醛(HCHO)溶液，用NaOH溶液调节体系pH为11.0，采用恒温磁力搅拌器调节水浴温度为50 ℃反应2 h，制得羟甲基聚丙烯酰胺(MPAM)；最后将MPAM稀释成0.31%的水溶液，按照MPAM与巯基乙酸(TGA)物质的量之比1∶3.2加入TGA，用NaOH溶液调节体系pH为4.75，利用恒温磁力搅拌器调节水浴温度为25 ℃，反应2 h，得到产物巯基乙酰化羟甲基聚丙烯酰胺(MAMPAM)[10,20].

1.3 含Cu(Ⅱ)水样的配制

先用CuCl2·2H2O和蒸馏水配制成Cu(Ⅱ)浓度为10 000 mg/L的Cu(Ⅱ)储备液，然后用自来水将其稀释成试验所需浓度的水样.

1.4 试验方法

1.4.1絮凝试验

取400 mL含Cu(Ⅱ)水样于烧杯中，用HCl溶液调节水样pH至所需值，置于程控混凝试验搅拌仪中搅拌，投加不同量的MAMPAM后分别进行一定时间的快速和慢速搅拌(快搅速率120 r/min，快搅时间2 min，慢搅速率30 r/min，慢搅时间20 min)，静置15 min后，用移液管移取距液面2 cm处的上清液，用原子吸收分光光度计测定Cu(Ⅱ)的剩余浓度.

1.4.2响应面试验

根据课题组前期试验结果[20]，选取水样初始pH、Cu(Ⅱ)初始浓度以及MAMPAM投加量/Cu(Ⅱ)初始浓度为影响因素，分别记为X1、X2、X3，以+α、+1、0、-1、-α(α取1.682)分别代表各因素的水平值，以Cu(Ⅱ)去除率为响应值，记为Y，利用CCD试验建立MAMPAM除Cu(Ⅱ)的响应面模型，试验因素编码及水平值如表1所示. 该文响应面试验方案中所有絮凝试验均在实验室室温下进行.

表 1 CCD试验因素编码及水平Table 1 Codes and levels of experimental factors of CCD

2 结果与讨论

2.1 MAMPAM的性质

试验制得的MAMPAM为无色透明液体，pH为4.54，特性黏度为0.070 mg/L，易溶于水和甲醇，不溶于乙醇、丙酮和乙醚[23].

2.2 残差分析

将影响因素及其水平值(见表1)录入到Design-Expert 8.0.6软件中，软件推荐了20组试验方案，按照此方案分别进行MAMPAM除Cu(Ⅱ)的絮凝试验. 对试验值、响应值、残差、正态分布概率等进行残差分析，结果如图1所示，试验方案与结果如表2所示.

图 1 试验结果的残差分析Fig.1 Residual analysis of experimental results

表 2 CCD试验方案与结果Table 2 Experimental design and results of CCD

残差是试验值与响应值之间的差值，可以用来考察模型的合理性和数据的可靠性. 图1(a)中试验值与响应值的点基本在一条直线上，决定系数R2为0.915 4，20组絮凝试验的试验值与响应值较接近(见表2)，说明模型的拟合性较好[24]. 图1(b)中残差与响应值的点围绕残差为零的直线随机分布，没有任何规律，残差值分布在±3.50以内，说明模型误差较小、拟合度较高[25]. 图1(c)中残差与正态分布概率的点基本在一条直线上，置信度为93%，在95%以内，表明残差服从正态分布[26-27]. 图1说明模型的合理性、拟合性均较好，可以用来优化MAMPAM除Cu(Ⅱ)的絮凝条件.

2.3 方差分析

利用Design-Expert 8.0.6软件对表2中Cu(Ⅱ)去除率的试验值进行方差分析，结果如表3所示；以编码值表示的响应面模型的三元二次回归方程如式(1)所示.

由表3可知，模型的F值为12.75，P值为0.000 2(＜0.001)，表明模型非常显著；模型失拟项的F值为4.84，P值为0.054 2 (＞0.05)，表明模型的失拟项不显著，说明模型合理，可以用模型的响应值来代替试验值[28]；模型的决定系数R2值为0.919 9，校正决定系数Radj2值为0.847 7，表明模型的拟合度较高；模型的精密度值为13.737(＞4)，表明模型的精密度较高，可以利用响应值预测实际值[29].X1、X2、X3的P值分别为0.003 4、0.073 2、0.000 5，说明X1、X3为显著影响因素，X2为不显著影响因素；X12、X22、X32的P值分别为0.713 4、0.888 2、＜0.000 1，说明X32的曲面效应非常显著，X12、X22的曲面效应不显著[22].

表 3 模型的方差分析Table 3 Variance analysis of model

2.4 响应面分析

利用Design-Expert 8.0.6软件分析水样初始pH(X1)、Cu(Ⅱ)初始浓度(X2)以及MAMPAM投加量/Cu(Ⅱ)初始浓度(X3)中单一因素对Cu(Ⅱ)去除率的影响以及两两因素的交互作用对Cu(Ⅱ)去除率的影响，即固定其中一个因素，以Cu(Ⅱ)去除率(Y)为响应值，以另外两个因素为变量绘制等高线图和响应面图.

2.4.1水样初始pH与Cu(Ⅱ)初始浓度的交互作用

固定MAMPAM投加量与Cu(Ⅱ)初始浓度的比值为4.0∶1，Cu(Ⅱ)初始浓度为60.0~130.0 mg/L，水样初始pH为4.0~6.0时，Cu(Ⅱ)去除率的等高线图和响应面图如图2所示.

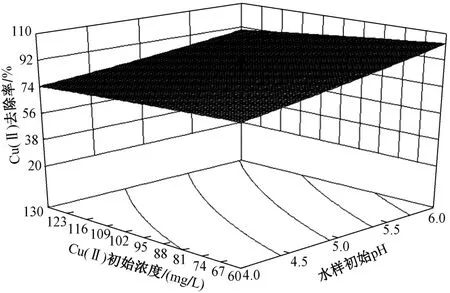
图 2 水样初始pH与Cu(Ⅱ)初始浓度的交互作用Fig.2 Interaction between initial pH value and initial concentration of Cu(Ⅱ)

由图2可以看出，等高线接近圆形，并且从表3可知，P(X1X2)=0.586 9(＞0.05)，说明水样初始pH与Cu(Ⅱ)初始浓度之间的交互作用不显著[30-31]. 图2表明，当Cu(Ⅱ)初始浓度不变时，Cu(Ⅱ)去除率随着水样初始pH的增加而升高. 这可能是因为在pH较低的条件下，MAMPAM分子链中的巯基主要以-SH的形式存在，由于质子化作用不利于与Cu(Ⅱ)发生螯合反应生成絮体；当pH升高，MAMPAM分子链中的巯基发生解离，主要以-S-的形式存在，易与Cu(Ⅱ)发生螯合反应，可形成大量不溶态Cu(絮体)，Cu(Ⅱ)去除率相应提高[10]. 当水样初始pH不变时，Cu(Ⅱ)去除率随着Cu(Ⅱ)初始浓度的增加而降低，这可能是因为MAMPAM投加量/Cu(Ⅱ)初始浓度的值是固定的，随着Cu(Ⅱ)初始浓度的增加，MAMPAM的投加量也在增加，当水样中MAMPAM的投加量超过了最佳投药量时，所生成的细小絮体周围就会出现大量带电荷的-S-，使得絮体间的静电斥力增大，影响了絮体的生长和沉降，出现絮体重新稳定现象，故Cu(Ⅱ)去除率反而下降. 图2还表明，当水样初始pH和Cu(Ⅱ)初始浓度同时增大时，Cu(Ⅱ)去除率变化不明显，表明二者的交互作用对Cu(Ⅱ)去除率的影响较小.

2.4.2水样初始pH与MAMPAM投加量/Cu(Ⅱ)初始浓度的交互作用

固定Cu(Ⅱ)初始浓度为95.0 mg/L，MAMPAM投加量与Cu(Ⅱ)初始浓度的比值为3.0:1~5.0:1，水样初始pH为4.0~6.0时，Cu(Ⅱ)去除率的等高线图和响应面图如图3所示.

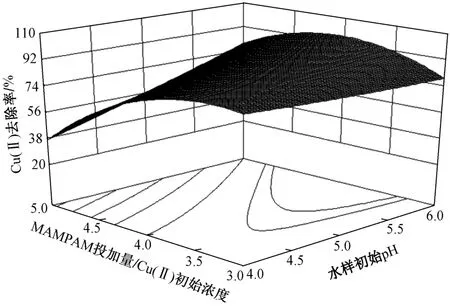
图 3 水样初始pH与MAMPAM投加量/Cu(Ⅱ)初始浓度的交互作用Fig.3 Interaction between initial pH value and the ratio of MAMPAM dosage to initial concentration of Cu(Ⅱ)

由图3可以看出，等高线接近于椭圆形，并且从表3可知，P(X1X3)=0.003 4(＜0.05)，说明水样的初始pH与MAMPAM投加量/Cu(Ⅱ)初始浓度的交互作用显著. 图3表明，当水样初始pH不变时，Cu(Ⅱ)的去除率随着MAMPAM投加量/Cu(Ⅱ)初始浓度比值的增加而先升高后降低. 这可能是因为Cu(Ⅱ)初始浓度是固定的，MAMPAM投加量/Cu(Ⅱ)初始浓度的值增加就意味着水样中MAMPAM投加量增加，水样中与Cu(Ⅱ)发生反应的巯基数量增多，生成絮体的数量增多，增加了絮体间的碰撞几率，可形成大的絮体颗粒，提高了絮体的沉降性，故Cu(Ⅱ)的去除率升高；但投药量继续增大后，所生成的絮体周围就会出现大量带负电荷的-S-，使得絮体间的静电斥力增大，絮体之间相互排斥，影响了絮体的生长和沉降，出现絮体重新稳定现象，故Cu(Ⅱ)的去除率反而下降[20].当MAMPAM投加量/Cu(Ⅱ)初始浓度不变时，Cu(Ⅱ)的去除率随着初始pH的增加而升高，原因与上面所述相同，即在较高pH条件下，MAMPAM分子链上的巯基发生解离，主要以-S-形式存在，易于与Cu(Ⅱ)螯合配位，形成不溶态Cu. 图3还表明，同时增大MAMPAM投加量/Cu(Ⅱ)初始浓度的值和水样初始pH，Cu(Ⅱ)的去除率升高，这可能是因为水样中的-S-的数量增多，与Cu(Ⅱ)螯合配位的能力增强，因此Cu(Ⅱ)的去除率有所升高，说明二者具有一定的协同作用.

2.4.3Cu(Ⅱ)初始浓度与MAMPAM投加量/Cu(Ⅱ)初始浓度的交互作用

固定水样初始pH为5.0，Cu(Ⅱ)初始浓度为60.0~130.0 mg/L，MAMPAM投加量与Cu(Ⅱ)初始浓度的比值为3.0∶1~5.0∶1时，Cu(Ⅱ)去除率的等高线图和响应面图如图4所示.

图 4 Cu(Ⅱ)初始浓度与MAMPAM投加量/Cu(Ⅱ)初始浓度的交互作用Fig.4 Interaction between initial concentration of Cu(Ⅱ) and the ratio of MAMPAM dosage to initial concentration of Cu(Ⅱ)

由图4可以看出，等高线接近于椭圆形，说明X2、X3的交互作用显著；但是从表3可知，P(X2X3)=0.193 4(＞0.05)，表明X2、X3的交互作用不显著. 上述两种方法获得的结果相矛盾，这可能是因为P值的大小仅表示试验数据在统计学上是否显著，不能完全代表在实际案例中的显著性，在实际应用中需将P值与实际问题结合起来考虑[32]. 因此，在该研究中可以根据等高线趋近于椭圆形说明Cu(Ⅱ)初始浓度与MAMPAM投加量/Cu(Ⅱ)初始浓度的交互作用是显著的. 图4表明，当Cu(Ⅱ)初始浓度不变，Cu(Ⅱ)的去除率随着MAMPAM投加量/Cu(Ⅱ)初始浓度值的增加而先升高后降低，原因与前述相似，即随着MAMPAM投加量/Cu(Ⅱ)初始浓度值的增加，水样中的MAMPAM的数量增加，易于与Cu(Ⅱ)螯合配位形成不溶性Cu；当MAMPAM的数量超过最佳投药量时，水样中的负电荷增多，絮体之间相互排斥，不利于絮凝沉淀.当MAMPAM投加量/Cu(Ⅱ)初始浓度不变，Cu(Ⅱ)的去除率随着Cu(Ⅱ)初始浓度的增加而降低，原因与上面所述相似. 图4还表明，当同时增大Cu(Ⅱ)初始浓度和MAMPAM投加量/Cu(Ⅱ)初始浓度(即MAMPAM投加量增加)时，Cu(Ⅱ)的去除率降低，这可能是因为同时增大Cu(Ⅱ)初始浓度和MAMPAM的投加量，使得絮体周围出现大量带负电荷的-S-，使得絮体间的静电斥力增大，影响絮体的稳定性，使得部分絮体出现重新稳定的现象，因此Cu(Ⅱ)的去除率反而下降，说明二者具有一定的拮抗作用.

2.5 响应面模型验证

确定响应面优化试验最佳絮凝条件一般有两种方法：一是Design-Expert 8.0.6软件推荐的最佳絮凝条件；二是根据模型回归方程求偏导为零得到的最佳絮凝条件，分别在两组絮凝条件下进行絮凝试验.

Design-Expert 8.0.6软件推荐的最佳絮凝条件：水样初始pH为5.8，Cu(Ⅱ)初始浓度为65.6 mg/L，MAMPAM投加量与Cu(Ⅱ)初始浓度的比值为3.7∶1.在此条件下进行絮凝试验，测得Cu(Ⅱ)的平均去除率为95.05%，模型预测的去除率为98.52%，相对偏差为-3.52%.

模型的回归方程如式(1)所示，将式(1)分别对X1、X2、X3求偏导，并且令其偏导为零得到三元一次方程组，该三元一次方程组的解即为最佳絮凝条件.其计算结果为：水样初始pH为4.0，Cu(Ⅱ)初始浓度为85.2 mg/L，MAMPAM投加量与Cu(Ⅱ)初始浓度的比值为3.3∶1. 在此条件下进行絮凝试验，测得的平均去除率为83.98%，模型预测的去除率为87.17%，相对偏差为-3.66%.

对比两种方法下的最佳絮凝条件，Design-Expert 8.0.6软件推荐的最佳絮凝条件的去除率较高，试验值与响应值之间的相对偏差较小，故选用软件Design-Expert 8.0.6推荐的最佳絮凝条件，即水样初始pH为5.8、Cu(Ⅱ)初始浓度为65.6 mg/L、MAMPAM投加量与Cu(Ⅱ)初始浓度的比值为3.7∶1. 管映兵等[20]在水样初始pH为6.0、Cu(Ⅱ)初始浓度为25.0 mg/L、MAMPAM投加量与Cu(Ⅱ)初始浓度的比值为4.8∶1的条件下进行絮凝试验，测得Cu(Ⅱ)的平均去除率为95.30%，与该文响应面法确定的最佳絮凝条件相比，Cu(Ⅱ)的平均去除率相当，但该研究处理的含Cu(Ⅱ)废水中Cu(Ⅱ)初始浓度更高，MAMPAM投加量与Cu(Ⅱ)初始浓度的比值更低(即相对投加量更低)，表明利用响应面法可以更好地优化MAMPAM除Cu(Ⅱ)的絮凝条件.

3 结论

a) 响应面法中的CCD试验可以很好地优化重金属絮凝剂MAMPAM去除水样中Cu(Ⅱ)的絮凝条件，建立的模型显著、拟合性好、精密度和可信度较高.

b) 模型的方差分析和响应面分析表明：水样初始pH(X1)、MAMPAM投加量/Cu(Ⅱ)初始浓度(X3)为显著影响因素，Cu(Ⅱ)初始浓度(X2)为不显著影响因素；X1X3、X2X3之间的交互作用显著，X1X2之间的交互作用不显著.

c) 通过响应面模型验证试验得到最佳絮凝条件为软件推荐条件，即水样初始pH为5.8、Cu(Ⅱ)初始浓度为65.6 mg/L、MAMPAM投加量与Cu(Ⅱ)初始浓度的比值为3.7∶1，在此条件下进行絮凝试验，试验测得的平均去除率与模型预测的去除率的相对偏差为-3.52%，证明建立的模型可靠.