基于RLMD和WSET的变转速下滚动轴承故障诊断*

柯 伟,金仲平,吕信策,刘双辉

(1.台州市特种设备检验检测研究院,浙江 台州 318000;2.武汉科技大学 机械自动化学院,湖北 武汉 430081)

0 引 言

滚动轴承作为起重机、风机等大型机械设备的关键部件,起着承载转轴和轴上零件的重要作用。但由于其工作环境的复杂性,滚动轴承是最主要的故障来源之一[1]。其故障往往会导致设备异常甚至引起重大安全事故,造成严重人员伤亡及经济损失。因此实现滚动轴承的健康状态监测和故障诊断,对安全生产具有重要的意义。

经验模态分解(empirical mode decomposition,EMD)方法在滚动轴承故障诊断中已被广泛采用。但EMD存在着模态混合的缺点,误差积累很容易造成分解结果失真[2]。

变分模态分解(variational mode decomposition,VMD)方法能够将信号分解为若干个具有一定中心频率和带宽的模态分量,然而VMD很难快速、准确地确定预设的分解层数K和二次惩罚因子等参数[3]。

局部均值分解(local mean decomposition,LMD)方法将信号分解为乘积函数(product function,PF)之和,能够很好地反映非平稳信号的时-频分布特性[4],已被应用于滚动轴承故障诊断领域[5];但是LMD依然存在模态混叠现象,使得分解结果容易产生偏差,导致故障诊断的准确度不高。

LIU Zhi-liang等人[6]研究了鲁棒局部均值分解(RLMD)方法,有效地解决了上述问题,并将其引入到多分量调幅调频信号的分析中;相比于其他模式分解算法,RLMD能够用于准确地识别出不同类型的模式分量[7]。因此,选择RLMD对变转速下滚动轴承振动信号进行预处理,消除噪声等无关分量的影响,可以为后续对多组分信号进行时频分析提供基础。

由于理论上的不足,短时傅里叶变换(short-time Fourier transform,STFT)[8]和连续小波变换(continuous wavelet transform,CWT)[9]等传统时频分析方法的计算结果在时频面上能量不够集中。DAUBECHIES I等人[10]研究了同步压缩变换(synchro squeezing transform,SST),在STFT或CWT的基础上进行瞬时频率(instantaneous frequency,IF)估计,然后将时频能量沿着频率轴进行重新分配,能够揭示非平稳信号复杂的时频特性。

然而为了保证多分量信号的分解和重构,SST牺牲了一部分能量聚集性[11]。YU Gang等人[12]在SST的基础上,研究了同步提取变换(synchro extracting transform,SET)方法。基于STFT的计算结果,利用同步提取算子(synchro extracting operator,SEO)替代SST中的同步压缩算子,可以进一步提高时频能量聚焦性[13]。

但是STFT受到窗函数的影响,而CWT中存在一系列小波基函数,小波窗口的长度可以随尺度变化,时间-频率分辨率具有更好的适应性。因此SHI Zhen-jin等人[14]研究了基于CWT的同步提取变换(WSET)方法。相比于基于STFT的SET,WSET的核心思想是只提取信号在瞬时频率对应尺度下的小波变换时频谱,去掉了不关心的时频能量,可以获得高聚集性的时频表达。

对于包含噪声等成分的多组分振动信号,为了获得清晰集中的时频表达,需要对信号进行预处理。常见的滤波降噪等方法难以确定滤波的频带,经常会造成将有效分量误消除的现象。

因此,笔者提出基于RLMD和WSET的滚动轴承故障诊断算法,即首先对变转速工况下滚动轴承振动信号进行RLMD分解,利用分解分量与原始信号之间最大互相关系数的原则选择最佳分量,有效去除噪声等其他分量的影响;然后对选取的最佳分量作WSET时频分析,获得集中清晰的时频谱;最后进行脊线提取与变转速下的故障类型识别,进行数值模拟仿真与变转速试验台数据对比分析,以验证该方法的可行性。

1 理论描述

1.1 故障特征频率

滚动轴承的故障通常包括内圈故障、外圈故障、滚动体故障、保持架故障等类型。当轴承存在故障时,滚动体每转过一圈时会产生冲击,产生冲击的间隔即为该故障对应的故障特征频率。

采用经验公式可知,不同类型故障的故障特征频率与转频fr、滚动体个数z的关系描述如下[15]:

外圈故障特征频率fo为:

fo=0.4·z·fr

(1)

内圈故障特征频率fi为:

fi=0.6·z·fr

(2)

滚动体故障特征频率fc为:

fc=(0.381～0.4)·fr

(3)

保持架故障特征频率fb为:

(4)

在变转速工况下,由于转频fr的变化,故障特征频率在时频面上表现出来的是一条时频脊线。因此,利用时频分析方法如何准确地从时频面中获取这条曲线,成为了变转速故障诊断的研究重点。

1.2 鲁棒局部均值分解

对于任一复杂的待分析信号s(t),LMD都可将其分解为若干PF分量与残余项uk的和,即:

(5)

其中,每个PF分量都可以表示为一个调频信号与一个包络信号的乘积函数,这些PF分量包含了原始信号在多个尺度上的信息。

在LMD的基础上,RLMD的第一步是确定局部极值。

如果信号s(t)的端点不是极值,则会在随后端点的包络估计中产生错误,可能导致发散的现象,影响到迭代过程中PF分量的提取,结果将不能反映原始信号的特性。

为了处理信号端点,笔者提出的RLMD采用镜像扩展算法。该算法的过程简述如下:

(1)确定信号左右两端的对称点;

(2)对步骤(1)中确定的对称点进行信号镜像扩展,利用扩展率控制扩展信号的总长度;

(3)对扩展信号执行滑动平均算法[16],然后截取与原始信号相同长度进行后续计算。

RLMD的第二步是进行包络估计。

首先计算信号s(t)的所有局部均值mi(t)及其对应局部包络估计值ai(t)的所有步长,其步长在数值上等于(ek+1-ek)+1;然后计算信号在每个步长和步长边缘中的概率,分别以B(k)和edge(k)表示。

定义步长中心us和步长标准偏差γs为:

(6)

(7)

式中:Nb—步长的个数。

信号在每个步长和步长边缘中的概率,即B(k)和edge(k)的表达式为:

b(k)=(edge(k)+edge(k+1))/2

(8)

最后,选择的子集大小τ表达式为:

τ=odd(us+3×γs)

(9)

式中:odd(·)—将其输入舍入为大于或等于输入的最接近的奇数整数的函数。

迭代过程的终止条件为:

(10)

RLMD提出包络信号的目标函数定义如下:

f=R(α(t))+K(α(t))

(11)

α(t)=ai(t)-1

(12)

式中:R(α(t))—α(t)的均方根;K(α(t))—α(t)的过峰度。

分别定义为:

(13)

(14)

RLMD为每个PF分量给出一个包络信号ai(t)和一个调频信号si(t)。显然,第i个PF分量的瞬时振幅是包络信号ai(t)。

调频信号si(t)第i个PF的瞬时相位和频率可以用下式导出:

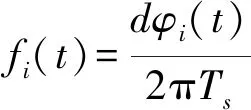
(15)

利用RLMD对信号进行分解,能够较好地解决边界条件、包络估计、迭代终止条件的影响,获得反映信号本质特征的有用模式分量。

1.3 同步提取小波变换

信号s(t)经过RLMD分解后,笔者以分量与原始信号之间的最大互相关系数作为选择标准,选择PFp(t)(p=1,2,…,k)与信号s(t)之间互相关程度最大的分量x(t):

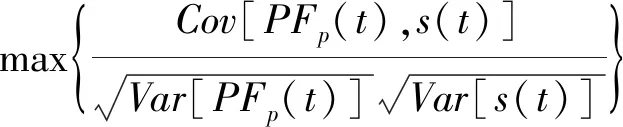
(16)

对于选择的分量x(t),其STFT公式描述为:

(17)

式中:g(t)—Schwartz空间中的窗函数。

x(t)的CWT公式描述为:

(18)

式中:t—平移参数,s;a—尺度参数,无单位;ψ—实小波基函数,无单位。

基于STFT的同步提取变换SET写为:

Te=V(t,ω)·δ(ω-ω0(t,ω))

(19)

式中:ω0(t,ω)—信号的瞬时频率。

通过STFT的瞬时频率估算公式为:

(20)

同步提取算子δ(ω-ω0(t,ω))满足以下条件:

(21)

(22)

基于CWT的同步提取变换WSET定义为:

(23)

式中:δ(a-aω)—基于CWT的同步提取算子。

δ(a-aω)的表达式为:

(24)

则WSET可写为:

(25)

由上式可以发现,WSET在Wf(t,a)的时频面中对IF轨迹进行了同步提取,即a=aω,并将其他部分去掉。

由于SET受到了STFT具有固定TF分辨率的缺点的限制,在处理快速变化或含噪的多分量信号时,它不能给出更高的TF分辨率。SET与WSET在对含噪信号的处理能力将在数值模拟仿真中进行比较。

1.4 基于RLMD和WSET的故障诊断方法

基于RLMD和WSET的滚动轴承故障诊断方法为:

(1)首先利用RLMD对信号进行分解,计算分解的每个分量与原始信号的互相关系数,选择互相关程度最大的分量为最佳分量,降低环境噪声、系统结构共振等的影响;

(2)然后对这个分量作WSET,获得分量时频谱;

(3)对WSET时频谱进行脊线提取,将提取脊线与理论故障特征频率曲线进行比较,从而实现对变转速工况下滚动轴承的故障诊断。

笔者提出方法的算法流程图如图1所示。

图1 算法流程图

2 数值模拟仿真

2.1 时变仿真信号定义

为说明RLMD和WSET的优越性,笔者首先进行模拟仿真实验。定义时变仿真信号由3个分量组成,公式描述为:

s1(t)=0.1sin(50t)
s2(t)=0.4sin[2π(100t+5t2)]
s3(t)=0.3sin[2π(180t+sin(4πt))]
s(t)=s1(t)+s2(t)+s3(t)+n(t)

(26)

式中:s1(t)—恒定分量;s2(t)—线性分量;s3(t)—调频分量。

笔者对信号添加SNR=2 dB的噪声n(t)。

模拟信号时域图、频谱如图2所示。

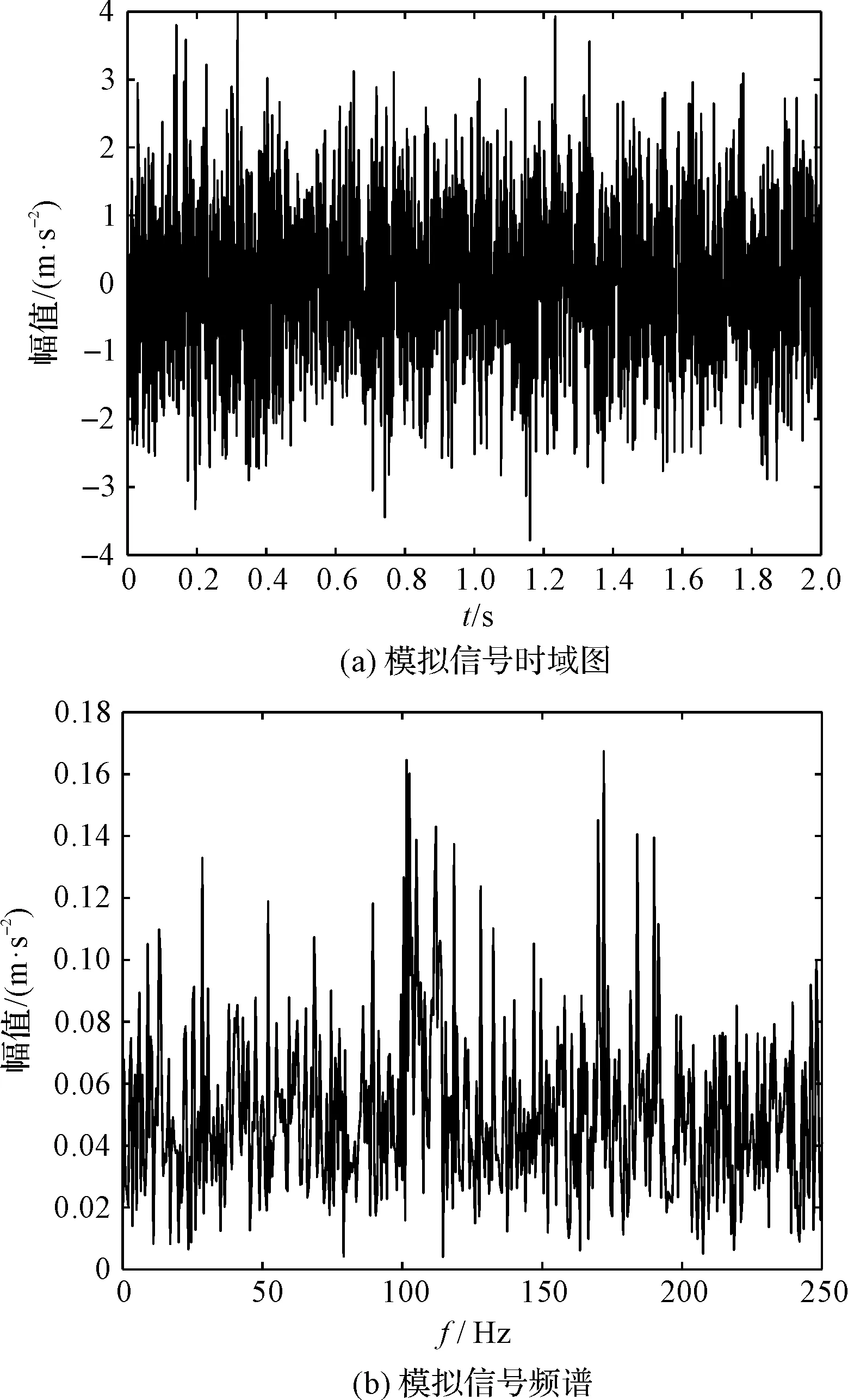
图2 模拟信号时域图及频谱

数值仿真信号的理想时频曲线如图3所示。

图3 理想时频曲线

2.2 利用信号分解算法进行降噪

由于噪声n(t)的影响,从信号频谱图2(b)中无法观察出3个分量所在的频率范围。笔者利用常见的模式分解算法对模拟信号进行处理。

EMD、VMD、LMD以及RLMD的分解结果如图4所示。

为了对比以上分解算法对信号分解的效果好坏,笔者对每个分解算法,选择互相关程度最大的分量,摒弃其他分量。

图4 4种算法的分解结果

4种算法分解结果的频谱如图5所示。

图5 4种算法分解结果的频谱

从图5中可以观察到:在EMD和VMD分解后的结果中并不能清晰看出分量信息,LMD能够模糊地看出2个分量的信息,而RLMD则可以完整看出3个分量的信息,并且将大部分噪声消除。因此,RLMD具有最好的模式分解效果。

2.3 利用时频分析方法进行特征提取

在图5的RLMD分解结果中,能够看出50 Hz的恒定分量,而对于100 Hz～130 Hz以及160 Hz～200 Hz附近的分量,在FFT频谱中难以进行判断,因此需要对分解结果进行时频分析。

STFT、CWT、SET、WSET 4种时频分析方法的计算结果如图6所示。

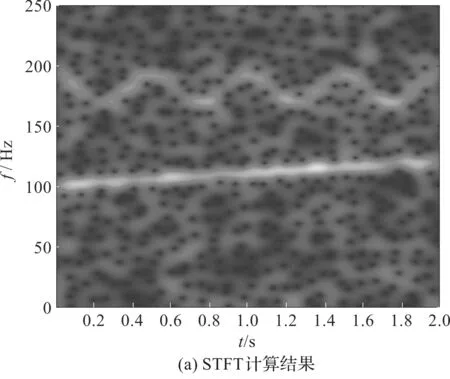
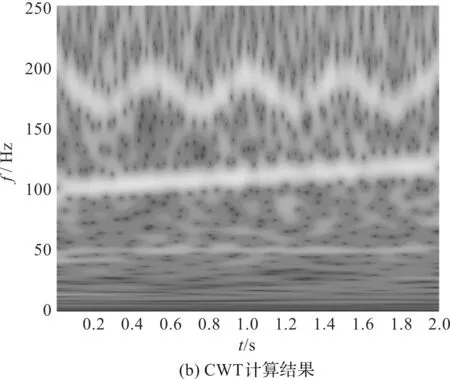
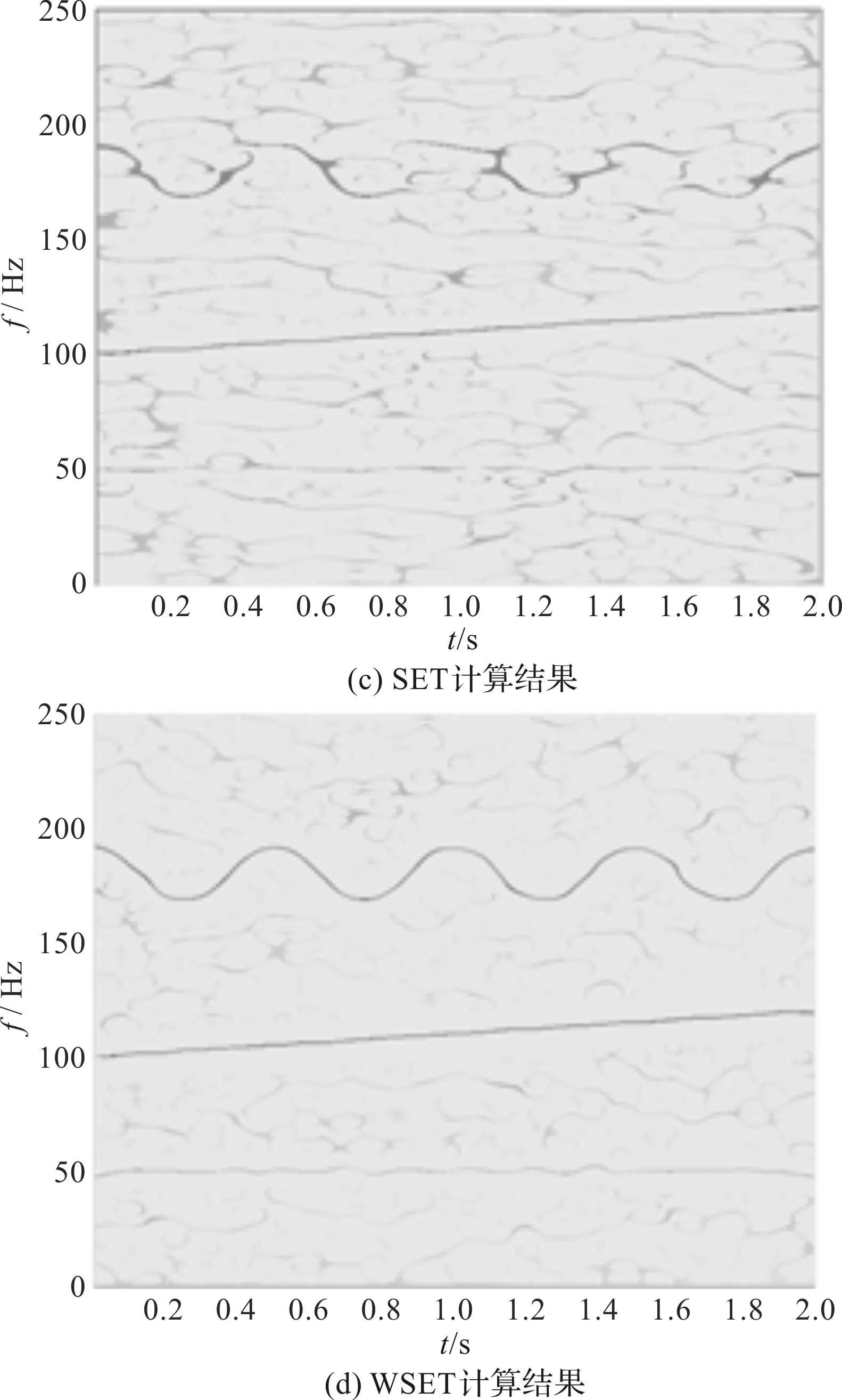
图6 4种时频分析算法的计算结果

对于以上4种时频分析算法的计算结果,STFT与CWT计算结果的时频表达模糊,不能清晰反映信号的3个分量,SET计算结果时频能量不够集中,且50 Hz的恒定分量无法识别出,而WSET则能够较好分辨出3个分量,具有较好的时频能量集中性。

另外,笔者计算4种时频分析方法的Renyi熵值来对时频分析结果进行定量判断。Renyi熵越低表示时频能量越集中,时频表达效果越好[17]。

4种时频分析算法的Renyi熵值如表1所示。

表1 4种时频分析算法的Renyi熵值

从表4可以发现,WSET具有最低的Renyi熵值,表明其时频面能量最为集中,具有最好的信号时频分析能力。

通过以上数值仿真可知,相比于其他的分解算法,RLMD对信号分解具有最好的效果,WSET对分解后的信号具有最好的时频刻画能力。仿真分析说明了笔者提出的基于RLMD和WSET的变转速滚动轴承故障诊断算法的有效性。

3 实验数据分析

3.1 实验装置介绍

为进一步验证基于RLMD和WSET的故障诊断方法的有效性,笔者以实验室轴承-齿轮故障综合试验台进行测试。轴承故障类型为外圈故障。

轴承-齿轮故障综合试验台及其结构简图如图7所示。

图7 轴承-齿轮故障综合试验台及其结构简图

实验台电机转速从0 r/min加速到1 500 r/min然后再减速到0 r/min;齿轮箱的减速比为5 ∶3;实验采样频率为1 280 Hz。

试验测点为A处滚动轴承,滚动轴承滚动体个数z=8。实验的目的在于对此处的滚动轴承进行故障诊断,测量振动信号时域图及频谱如图8所示。

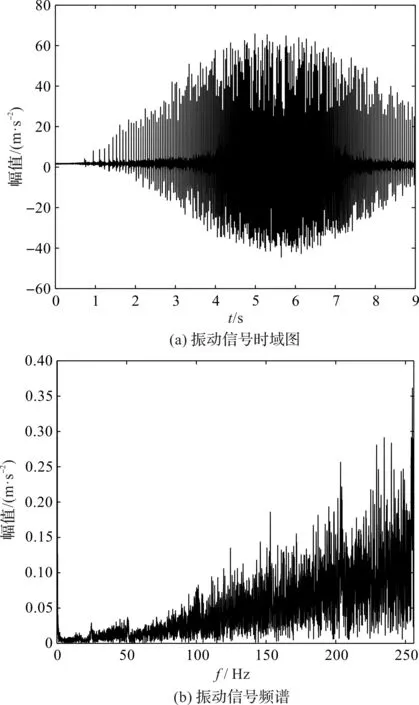
图8 测量振动信号时域图及频谱

3.2 基于RLMD的振动信号分解和降噪

由于信号为变转速过程中的振动信号,在频谱中无法进行有效分析,且信号包含有较多噪声,为了使信号时频分析更加准确,笔者首先应用RLMD进行降噪,以降低噪声等无关因素的影响。测量信号RLMD分解结果如图9所示。

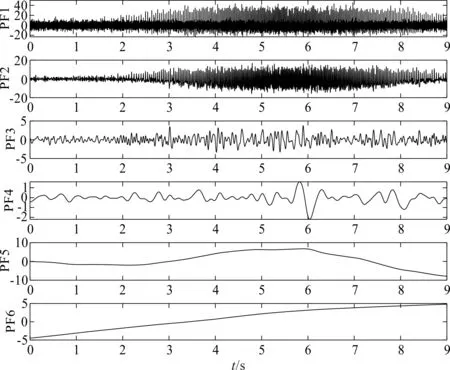
图9 测量信号RLMD分解结果

测量信号RLMD分解结果频谱如图10所示。

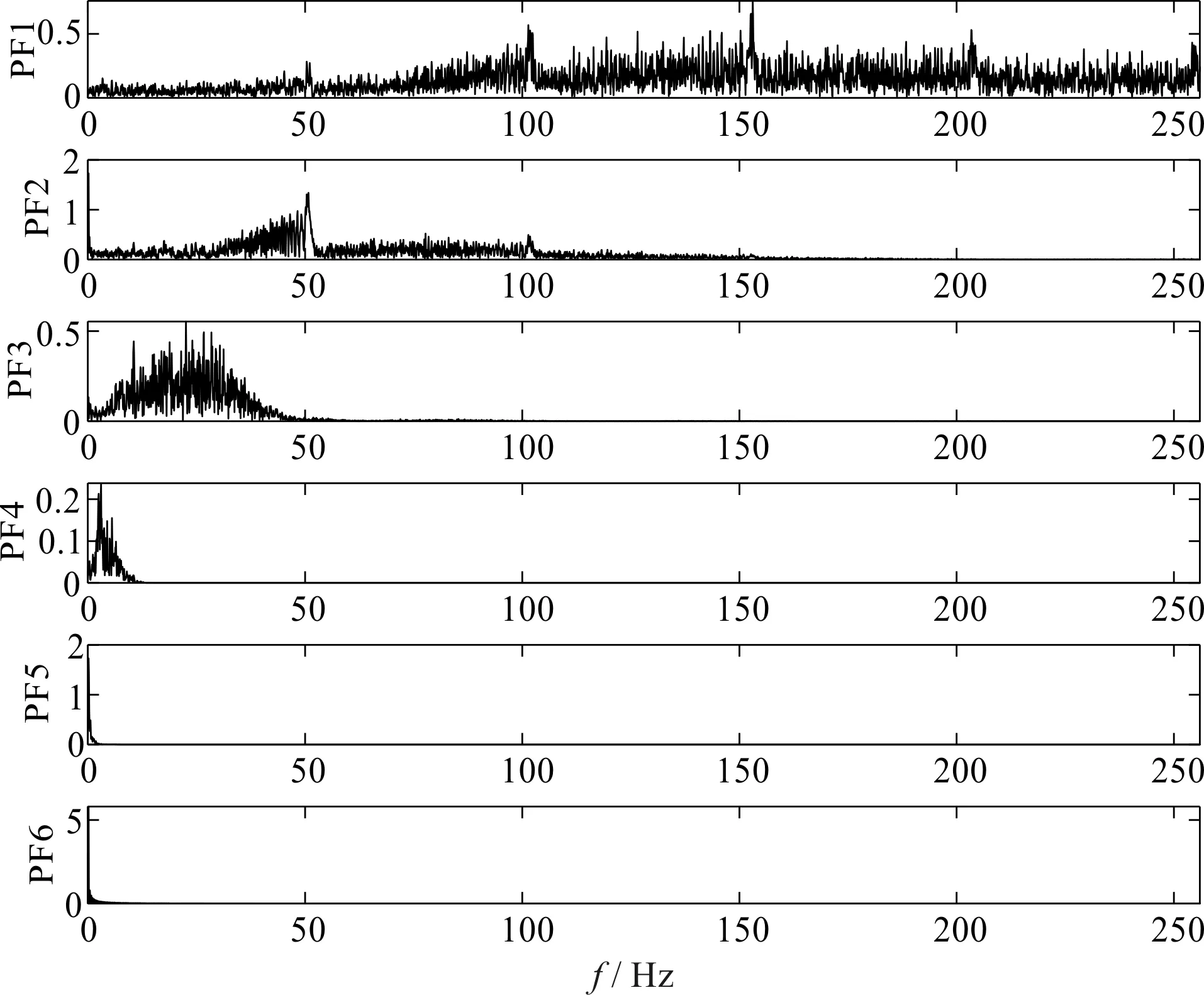
图10 测量信号RLMD分解结果频谱

3.3 基于WSET的时频分析和诊断

经过RLMD分解后,笔者依据最大互相关系数原则,选择分量PF1作为最佳分量,将信号中包含的噪声以及其他结构振动分量消除,通过观察图10的频谱信息。分解分量PF1中包含了0～50 Hz、50 Hz～100 Hz、100 Hz～150 Hz这样有规律性的3个部分,可以大概确定故障特征频率的在0～50 Hz之间,其2倍频及3倍则位于50 Hz～100 Hz、100 Hz～150 Hz之间。

对PF1分量的WSET提供的结果如图11所示。

图11 WSET提供的结果

从图11中可以清晰地看出,时频面脊线能量集中,以及故障特征频率fc及其倍频的存在。

未经RLMD分解信号WSET提供的结果如图12所示。

图12 未经RLMD分解信号WSET提供的结果

图12中,由于受到噪声等干扰,脊线能量发散和时频模糊,不利于进行脊线的提取。

笔者对图11的WSET结果进行脊线提取,WSET计算结果脊线提取结果如图13所示。

图13 WSET计算结果脊线提取结果

从图13中,可以清晰识别出故障特征频率fc及其各个倍频;通过转速计测量的转速,可以得到A轴承的转频曲线。

滚动轴承外圈故障特征频率的经验公式如下:

fo=0.4·z·fr

(27)

将理论外圈故障特征频率fo,以及WSET结果脊线提取的故障特征频率fc,以及转频fr绘制于一张图中,可得到脊线提取故障特征频率与理论值的比较,如图14所示。

图14 脊线提取故障特征频率与理论值的比较

试验台预设故障轴承图(外圈故障)如图15所示。

图15 试验台预设故障轴承图(外圈故障)

从图14中可以看出:WSET脊线提取的故障特征频率fc与理论外圈故障特征频率fo曲线几乎重合,因此,可以判断试验台滚动轴承故障为外圈故障,这与如图15所示的试验台预设故障一致。该结果验证了这种诊断方法的可行性。

4 结束语

在变转速工况下,对起重机、风机等重载设备中滚动轴承的故障诊断不够准确。针对这一问题,笔者提出了一种基于RLMD和WSET的滚动轴承故障诊断算法,该方法能够很好地消除噪声的影响,获得准确的故障特征频率曲线,在变转速滚动轴承故障诊断中具有有效性。

具体的研究结果为:

(1)利用RLMD对原始振动信号进行了分解,并基于最大互相关系数原则选择感兴趣的有效分量,能够较好地去除噪声、结构共振等无关分量;

(2)在RLMD分解的最佳分量上,对选取的最佳分量利用WSET进行了时频变换,获得了能量集中的时频表达,能够很好地提取出故障特征频率脊线;

(3)采用数值仿真的方式,对该方法的可行性进行了验证,对试验台滚动轴承数据分析的诊断结论与实验预设故障类型一致,验证了该方法在实际应用中的有效性。

由于笔者的研究仅仅针对转速变化工况下的振动信号,没有考虑变载荷、变温度等复杂工况。在后续的研究中,笔者将针对多种复杂工况下的振动信号降噪、特征提取等方面展开研究,以实现对于变工况下滚动轴承的精确故障诊断。