基于天牛群算法优化SVM的磨煤机故障诊断*
张 烨,黄 伟
(上海电力大学 自动化工程学院,上海 200090)
0 引 言
随着燃煤发电机组的容量不断增大,电厂辅助设备变得越来越重要。磨煤机一旦发生故障,不仅会影响锅炉的燃烧而降低整台机组的生产效率,而且会对其他设备以及生产工作人员的安全造成威胁。
孙栓柱等人[1]研究了磨煤机早期故障诊断方法,同时指出,在故障早期发现并诊断出磨煤机的故障,并让现场工作人员及时采取应对措施,具有非常重要的意义。
目前,故障诊断方法主要分为两大类,分别是基于模型的诊断方法和基于历史运行数据的诊断方法。
其中,基于模型的故障诊断方法需要先分析研究对象的机理,建立其数学模型。由于磨煤机工作时的机理过程非常复杂,很难获得准确的数学模型,故该方法的操作难度比较大。
而基于数据驱动的故障诊断方法主要是通过使用正常数据与历史异常数据对算法模型进行训练,模型对各种故障数据与正常数据自主学习分类,从而达到故障诊断的目的。
肖黎等人[2]研究了DBSCAN聚类方法,将历史数据分为正常数据与故障数据,建立了基于随机森林方法的磨煤机故障预警模型;该方法虽可以准确地标记磨煤机不同故障的发展阶段,但是在数据量不足和低维特征情况下,采用随机森林模型得到的分类结果不够理想。任梦祎等人[3]研究了采用马氏距离对故障特征进行预处理的方法,并基于过程记忆矩阵建立了非线性状态估计的磨煤机故障诊断模型;该方法虽在一定程度上提高了模型诊断的效率,但是很难用数学语言对实际故障进行描述,在工程上实现起来比较难。费树岷等人[4]对基于概率神经网络建立磨煤机故障分类器进行了研究,在数据处理阶段利用粗糙集对诊断参数的属性进行了筛选,所建立的模型能够在一定程度上提高分类的速度与精度;该方法虽取得了一定的效果,但是仍然存在一定的局限性,如神经网络的训练函数与网络层数选取不当,会导致其陷入局部最优问题,而在样本数据不够充足的情况下,又会出现过拟合现象。
刘定平等人[5]在最小二乘支持向量机的基础上建立了中速磨煤机的故障诊断模型,并且利用核主元分析方法对模型的训练参数进行了预处理,筛选出了和故障关联度最大的样本特征。将核主元分析方法与最小二乘支持向量机结合,可以有效地减少训练算法的输入特征数量,同时还可以利用支持向量机的非线性映射特点,在小样本情况下也可以很好地解决传统算法在学习过程中的过拟合问题。该模型能够在一定程度上满足诊断精度的要求,但是,由于支持向量机的诊断精度受到参数影响比较大,参数选取不当时,容易出现误诊断现象。
针对这一问题,笔者构建基于支持向量机的磨煤机故障诊断模型,并采用天牛群算法对模型参数中的惩罚因子C和核函数参数δ进行优化,最终建立BSO-SVM分类器,用该分类器诊断磨煤机故障。
1 支持向量机与天牛群算法
1.1 支持向量机
支持向量机(SVM)是由VAPICK V N[6]、LI Hua-qing[7]等人在20世纪90年代提出的,以统计学习理论为基础发展而来的一种新型机器学习方法。SVM具有训练时间短、模型精度高、训练样本少等优点。
SVM的原理是将输入数据通过核函数映射到高维空间进行分类,得到最大的分类间隙,然后映射回原空间,最后会得到分类函数:
(1)
式中:θi―拉格朗日乘子;b―根据训练样本确定的阈值;C―惩罚因子;K(x·xi)―核函数。
核函数的表达式为:
(2)
式中:δ―核函数参数。
SVM算法的具体步骤为:
(1)设置训练集M={(X1,Y1),(X2,Y2)…(Xn,Yn)},Xi∈Rn,Yi∈{-1,1}。
(2)选取适当的核函数K(x·xj)和惩罚参数C,构造并求解其最优化问题:
(3)
(4)
得到最优解θ*=(θ1*,θ2*,…θn*)T。
(3)选择θ*的一个正分量0<θ* (5) (4)根据θ*和b*构造分类函数: (6) 天牛群算法是在粒子群优化(PSO)算法[8]的基础之上,引入天牛须搜索对其位置更新规则进行改进的一种算法。 粒子群算法是一种模仿鸟类觅食的群体算法,群体中的个体通过不断更新自己的位置,然后相互比较得到最终解,个体更新取决于位置和速度。 算法的更新公式为: (7) (8) (9) (10) PSO算法收敛速度快,编程比较简单,因此被广泛用于各类参数优化。但是PSO算法的群体会受到单个粒子的影响,从而忽略对粒子本身的判断,导致全局搜索能力较差,有陷入局部最优解的缺陷,这使得其分类精度达不到最理想的状态。 为解决这个问题,笔者引入天牛须搜索策略[9,10],利用天牛须搜索对粒子群算法的更新规则进行了改进,构建了BSO-SVM故障分类模型。 天牛须搜索过程如下: (1)随机生成方向向量,并标准化: (11) 式中:D―空间维度;rands―随机函数。 (2)计算左、右须坐标: (12) (13) 式中:Xk―k时刻天牛的位置;dk―k时刻质心到须的距离。 (3)计算下一个时刻位置天牛的位置: (14) 式中:δk―k时刻的步长;f―适应度函数;sign()―符号函数。 (4)步长与搜索距离更新: δk+1=γ·δk (15) (16) 式中:γ―人为设定的衰减系数;C3―人为设定的变距离系数。 笔者将天牛须搜索中的位置更新策略引入到粒子群算法的粒子更新规则中,新的更新规则为: (17) (18) (19) 式中:Vbi―天牛群算法的速度更新率。 在粒子群算法的基础上,笔者改变其位置更新规则,其余规则与原算法保持一致。在新的规则下,粒子的位置更新不仅仅依赖历史最优解和当前全局最优解,还包括了粒子速度更新率。 改进的算法先对左须和右须位置进行比较,再决定群体的更新,尝试克服局部最优解问题。 SVM模型的惩罚因子C和核函数参数δ对分类精度有很大的影响[11-13]。笔者利用改进的粒子群算法对SVM参数进行优化,把SVM分类准确率作为适应度函数,再将得到的最优解赋值给SVM模型,达到对样本进行分类的目的。 BSO-SVM诊断模型流程图如图1所示。 图1 BSO-SVM诊断模型流程图 算法的具体实现过程如下: (1)BSO参数初始化,包括种群的数量、最大进化次数、惩罚因子C和核函数参数δ的上下界等。随机产生初始粒子和速度,计算初始粒子的适应度值; (2)判断终止条件是否满足,不满足则进入迭代部分,通过计算天牛左须值和右须值,再结合公式(17)生成速度更新规则,利用式(7,8,18)对粒子的速度进行更新;利用式(19)对粒子的下一个位置进行更新; (3)计算适应度值,更新个体最优值以及群体最优值。判断迭代是否结束,若结束,将最终得到的参数进行赋值,并用最优解训练SVM模型。 由于工作环境比较恶劣,磨煤机容易发生故障。磨煤机的故障主要分为两种,即设备故障和工艺故障。(1)设备故障主要包括磨煤机振动、磨煤机漏粉、主轴承过热、一次分管堵塞、磨煤机出力不足、磨煤机自燃、静压轴承油压异常;(2)工艺故障主要包括磨煤机满煤与磨煤机断煤[14]。这些故障中有些是可测故障,而有些是没有测点参数的故障。 笔者将对几种有测点参数的故障进行分类,分别是磨煤机断煤,磨煤机堵煤和磨煤机自燃。 当给煤管和一次风管发生堵塞、一次风量太小的时候,容易发生断煤的情况。由于给煤管堵塞,磨煤机的进煤量会减少,磨煤机里面的煤量过少导致剩余的煤没有办法吸收大量的热能,使得磨煤机出口温度升高。为了降低出口温度,在运行的过程中,一般会增大冷风门开度,同时减小热风门开度。此时磨煤机断煤,导致功耗下降。但是给煤机的转速有可能会偏高导致排粉机的功耗上升。 磨煤机断煤如图2所示。 图2 磨煤机断煤 当风量和煤量的比例失调的时候,如风量偏小或者煤量偏大,磨煤机里面的煤量会产生剩余,导致煤粉堆积,如果一次风没有办法及时将煤粉吹出磨煤机,就会产生磨煤机堵煤现象。如果原煤的水分含量较大,无法通过一次风使其彻底干燥,这种情况也会造成煤粉堆积,导致磨煤机堵煤。出现堵煤情况时,磨煤机的出口温度和出口粉流量会下降;磨煤机的电流会在效率下降时轻微上升,但是在堵煤情况比较严重的时候开始下降。 磨煤机堵煤如图3所示。 图3 磨煤机堵煤 磨煤机的出口温度升高到一定程度时,会导致磨煤机自燃。由前面的介绍可知,磨煤机发生断煤情况的时候会使得磨煤机出口温度上升;在磨煤机启停阶段,如果没有将磨煤机吹扫彻底,里面的积粉也可能会自燃;送入磨煤机的煤水分含量过低,煤粉无法吸收一次风送来的多余热量,磨煤机出口温度升高从而引起煤自燃。磨煤机发生自燃现象时,一次风的流量会降低,同时磨煤机的出入口风压降低。 磨煤机自燃如图4所示。 图4 磨煤机自燃 考虑到各个故障特征之间可能存在一定的耦合关系,而非彼此独立。笔者利用偏互信息方法[15]对7个故障特征进行筛选,分别为磨煤机电流、一次风差压、热风门开度、冷风门开度、煤粉流量、磨煤机出口温度、排粉机电流,并分别用t1、t2、t3、t4、t5、t6、t7表示。 对于多输入系统,输入变量为X,Y,输出变量为Z。当变量Y中包含变量X的信息时,需要将Y中X相关的信息剔除,公式为: (20) (21) 式中:n―样本个数;d―x维度;h―核函数宽度;∑―X的协方差矩阵。 mY(x)计算公式如下: (22) 剔除X相关信息后的Y和Z记为u和v: u=Y-mY(x) (23) v=Z-mZ(x) (24) 则Y和Z之间的偏互信息计算公式为: PMI(Y,Z)=I(u,v) (25) (26) 输入与输出之间的偏互信息越大表示其相关性越强。PMI算法筛选特征的步骤为: (1)令最佳变量集S为空集; (2)当输入变量不为空集时,计算u值与v值; (3)计算PMI值,将使其最大的变量进行排序; (4)组成最佳变量候选集合C; (5)计算AIC值,当其减小时,将对应变量放入最佳变量集合S,并返回第(2)步。 AIC值计算公式如下: (27) 式中:q―选择的变量个数。 当AIC第一个极小值出现时,最佳变量集合筛选结束。 通过PMI变量选择,得到最佳变量候选集合为{t6、t1、t2、t4、t5、t7、t3},特征选择如图5所示。 图5 特征选择 从图5可以看出,当选择3个变量时,AIC值达到最小。 根据算法规则,选择最佳变量候选集合中的前3个,即{t6、t1、t2}={磨煤机出口温度,磨煤机电流,一次风压差}。 笔者选择磨煤机出口温度、磨煤机电流、一次风差压3个变量作为算法模型的输入特征,分别用n1、n2、n3来表示3个特征。 实验数据信息如表1所示。 表1 实验数据信息 880个实验样本,每一类故障220个样本,笔者将其中各类故障样本的前176个样本作为训练集,后44个样本作为测试集;以分类器的分类准确率作为遗传算法(GA)、粒子群算法(PSO)与天牛须算法(BSO)的适应度函数。 属性矩阵有880行,表示880个样本;列数有4列,表示有4个属性。模型的输入是n1、n2、n3代表的故障特征,在模型输出中分别用1、2、3、4对正常状态和磨煤机断煤、磨煤机堵煤、煤自燃4个状态属性进行标记,称之为故障标签。 在故障诊断第一阶段,笔者使用604组带有故障标签的数据训练分类器;在第二阶段,使用不带故障标签的176个样本对分类器进行检验,即假设故障类型未知的情况下,将176个样本作为算法模型的输入,通过模型分类将样本划分成4种类型的状态,分别是正常状态和磨煤机断煤状态、磨煤机堵煤状态、磨自燃状态。 模型参数设置如表2所示。 表2 模型参数设置 PSO与BSO的初始参数设置大致相同,种群数量为20;种群迭代次数上限Kmax为200;搜索维度是2;权重设置为0.9;PSO的学习因子C1=0.5,C2=2;BSO的学习因子C1=0.5,C2=2,C3=3;惩罚因子C变化上限为100,下限设置为0.1;核函数参数δ变化上限为1 000,下限为0.01。 为了能够充分地体现算法的分类效果,考虑到此处建立的是多分类模型,故笔者选择宏平均后的准确率(Accave)、精确率(Preave)、召回率(Recave)、F1-score(F1ave)4个指标作为模型的评价标准。 各个指标的定义为: (28) (29) (30) (31) 式中:TPi―正例(第i类标签)的正确分类样本数;FNi―负例(除去第i类标签)的错误分类样本数;FPi―正例的错误分类样本数;number―磨煤机样本总数;n―磨煤机故障分类的类别数。 为了对模型的分类效果进行对比,笔者使用同一数据集,先分别利用遗传算法(GA)、粒子群算法(PSO)和天牛群算法(BSO)对支持向量机(SVM)的核函数参数δ与惩罚因子C进行优化,接着又将优化参数依次赋值给SVM,得到了3组组合模型(GA-SVM、PSO-SVM、BSO-SVM),最后用SVM、GA-SVM、PSO-SVM、BSO-SVM算法对磨煤机故障多分类模型进行检测。 迭代曲线如图6所示。 图6 迭代曲线 从图6中可以看出:GA与PSO提前收敛,陷入局部最优解,而BSO虽然进化代数比前面两种算法多,但是其最优解是三者中最大的;BSO比GA和PSO准确率更高,能够在一定程度上解决传统优化算法在寻优过程中陷入局部最优解问题。 参数优化结果如表3所示。 表3 参数优化结果 从表3可以看出,BSO算法优化结果为C=47.30,δ=4.13。 各模型分类结果如图7所示。 图7 各模型分类结果 从BSO-SVM模型的分类结果来看,图7上显示有5个样本被错误分类;其次,PSO-SVM模型和GA-SVM可以完成基本分类。 但是,在第3类和第4类故障中,这两种模型的识别不是很准确。PSO-SVM模型分类结果显示,有6个堵煤故障样本被误诊断为煤自燃故障,并且有7个煤自燃故障被误诊断为断煤故障;而采用默认初始参数的SVM模型对故障的分类结果较差,甚至将故障样本误诊断为正常样本。 模型评价指标如表4所示。 表4 模型评价指标 从表4可以看出:SVM模型使用未优化的初始值进行故障分类具有一定的随机性,其分类准确率最低,为78.13%(如果手动调整惩罚因子和核函数参数也可以使分类准确率提高,但是该方法随机性太强,而且会耗费大量手动设置的时间);BSO-SVM模型的分类准确率最高,为96.88%。 评价指标折线图如图8所示。 图8 评价指标折线图 图8中,相比于SVM模型、GA-SVM模型和PSO-SVM模型,BSO-SVM模型的Recave值分别高出0.36、0.16和0.17,F1ave值分别高出0.30、0.13和0.14。该结果说明,BSO-SVM模型不仅有较高的准确率,还有较高的稳定性。 考虑到在电厂实际运行过程中,传感器工作的环境比较恶劣,可能出现测量误差。为了验证BSO-SVM模型在有噪声干扰下的稳定性,笔者参考传感器误差标准,将噪声强度控制在5%~10%[16]。分别为176个测试样本添加噪声,即: y=y+k·ε·rand() (32) 式中:y—测试样本;k—控制系数;ε—样本标准差;rand()—随机函数。 笔者通过改变控制系数来产生不同强度的干扰,并以模型的准确度指标Accave和评价指标F1ave值作为模型稳定性测试指标,得到模型扰动测试的对比结果,如图9所示。 图9 模型扰动测试对比 从图9可以看出:在不同噪声的干扰下,BSO-SVM模型的变化最小,虽然其准确度和F1ave值在5类强度的噪声下有所下降,但是仍可以在4个算法模型中保持最高水平。 以上结果表明,BSO-SVM模型不仅可以提高故障分类的准确度,而且在算法稳定性方面也表现优秀,能够为磨煤机的故障诊断提供一定的参考。 采用基于最小二乘支持向量机的磨煤机故障诊断模型进行故障诊断时,支持向量机受到核函数参数和惩罚因子的影响较大,为此,笔者通过引入天牛须搜索策略对粒子群算法寻优过程进行了改进,解决了粒子群算法容易陷入局部最优解的问题,并将天牛群算法与支持向量机模型相结合,提出了一种基于BSO-SVM的磨煤机故障诊断方法;将该方法应用于磨煤机故障诊断,最后将其分别与GA-SVM、PSO-SVM、SVM进行了故障诊断结果比较。 研究结果如下: (1)通过仿真结果可知,相比于其他3种方法,BSO-SVM分类准确率最高,能够达到96.88%,这表明BSO-SVM模型能有效提高故障诊断精度; (2)天牛群(BSO)模型的全局搜索能力较强,能够解决粒子群(PSO)算法陷入局部最优解问题; (3)BSO-SVM模型的抗干扰能力比较强,在模拟传感器误差带来的噪声干扰实验中,在不同噪声强度环境下,BSO-SVM模型的评价指标F1ave始终能够保持最高水平。 由于笔者所使用的数据集是筛选出来的平衡数据集,而在实际电厂运行时,故障数据远远少于正常数据,存在大量的不平衡数据。在以后的研究中,笔者将使用不平衡数据集对模型进行校验,分析不平衡数据集对模型分类性能的影响。1.2 天牛群算法
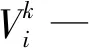
1.3 BSO-SVM算法流程
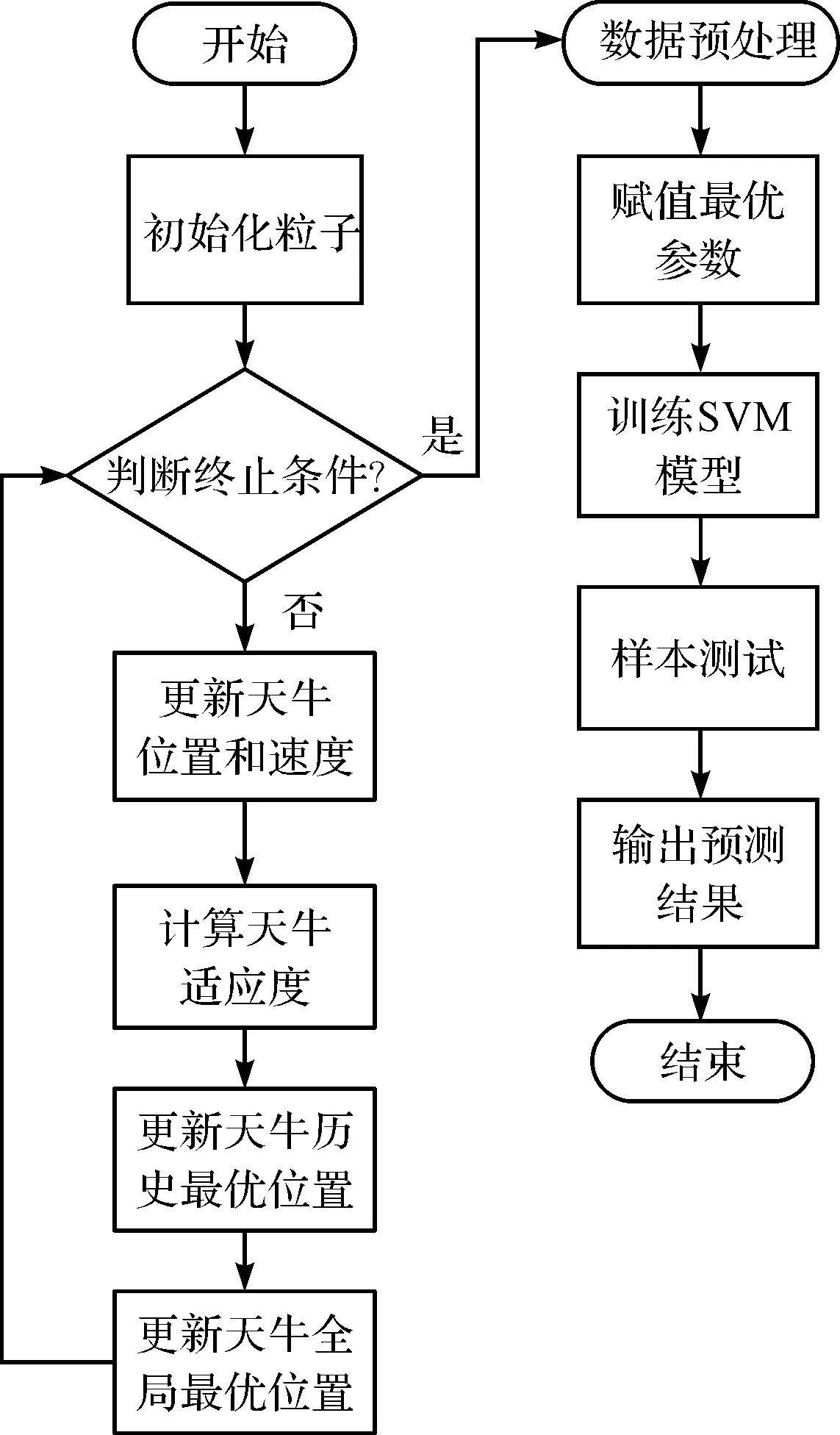
2 磨煤机故障分析
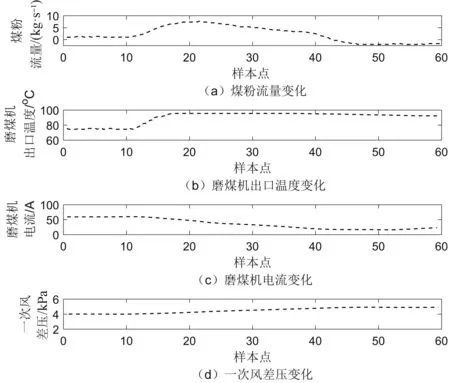
2.1 磨煤机断煤
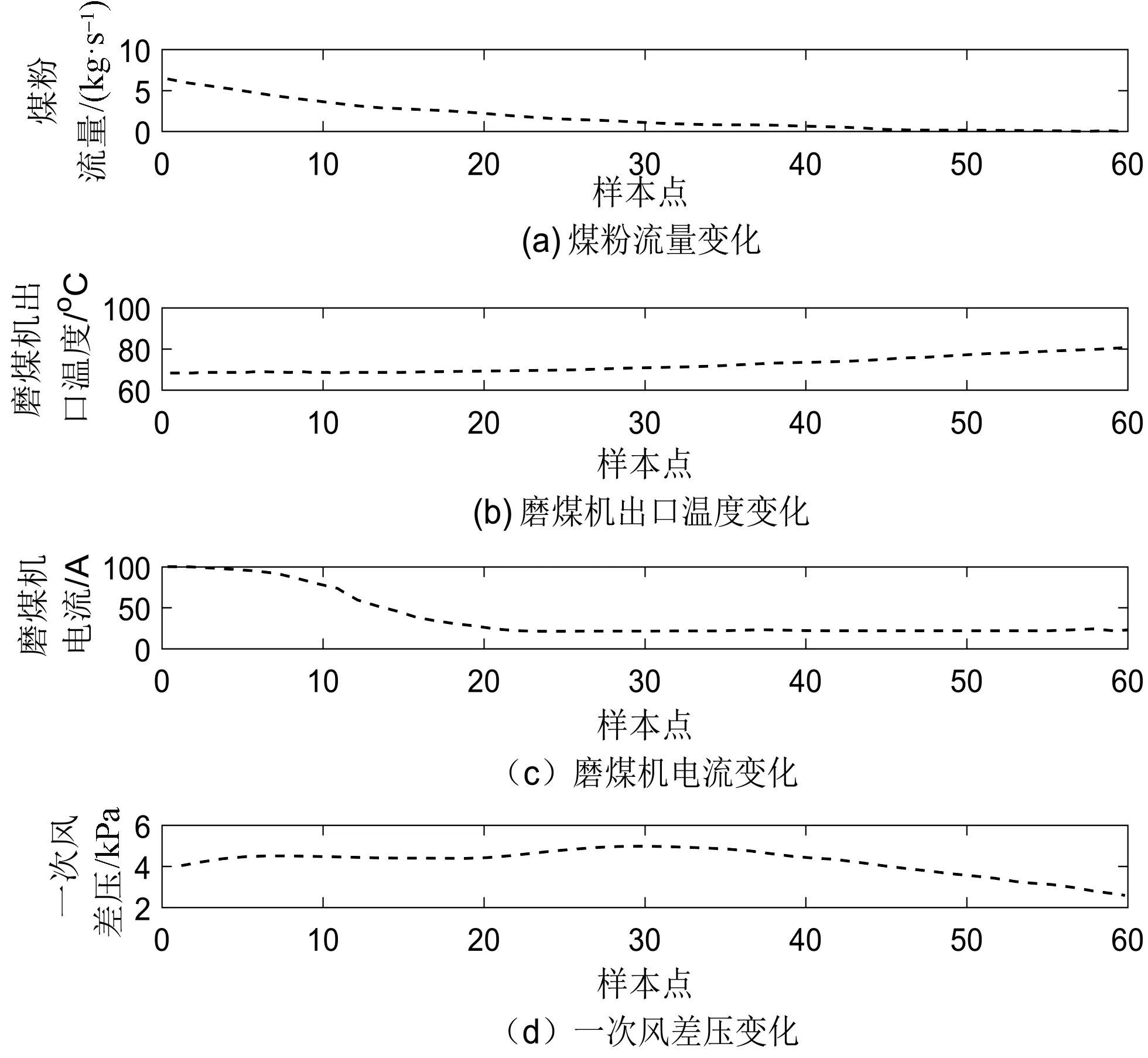
2.2 磨煤机堵煤
2.3 磨煤机自燃
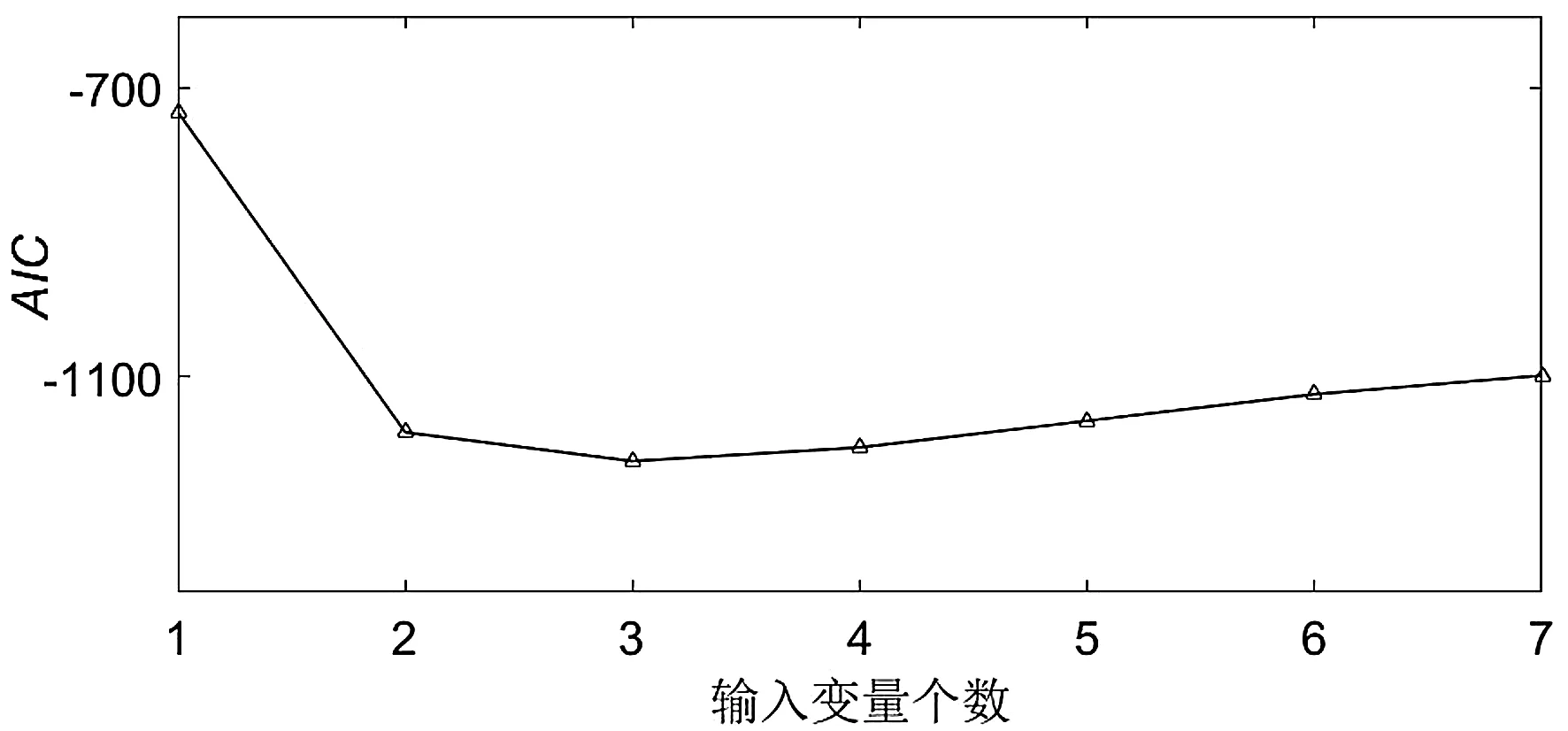
2.4 故障特征选择
3 实验及结果分析
3.1 实验数据准备

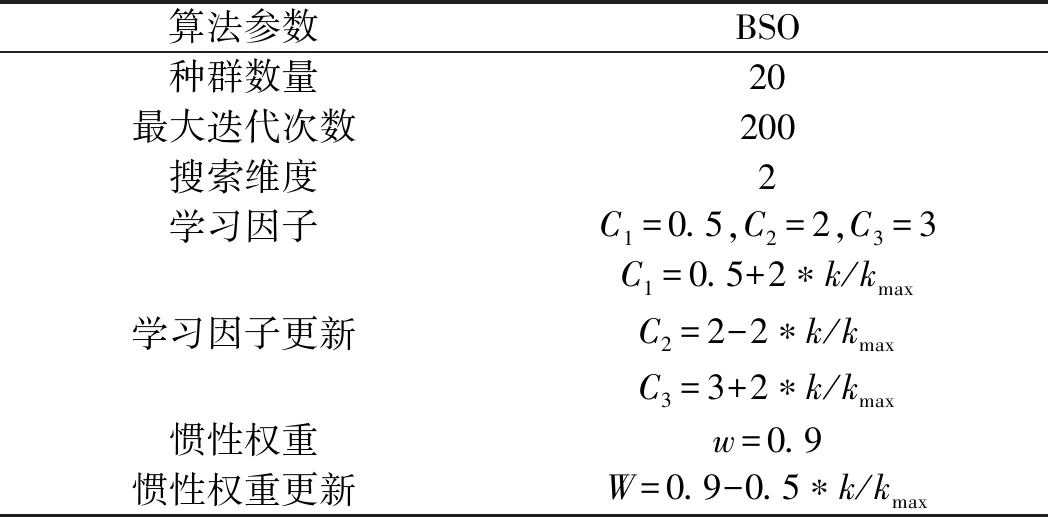
3.2 模型评价指标
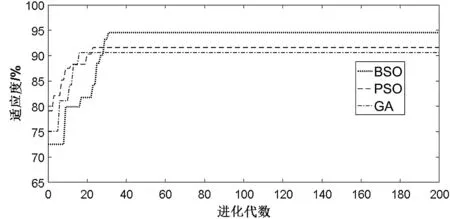
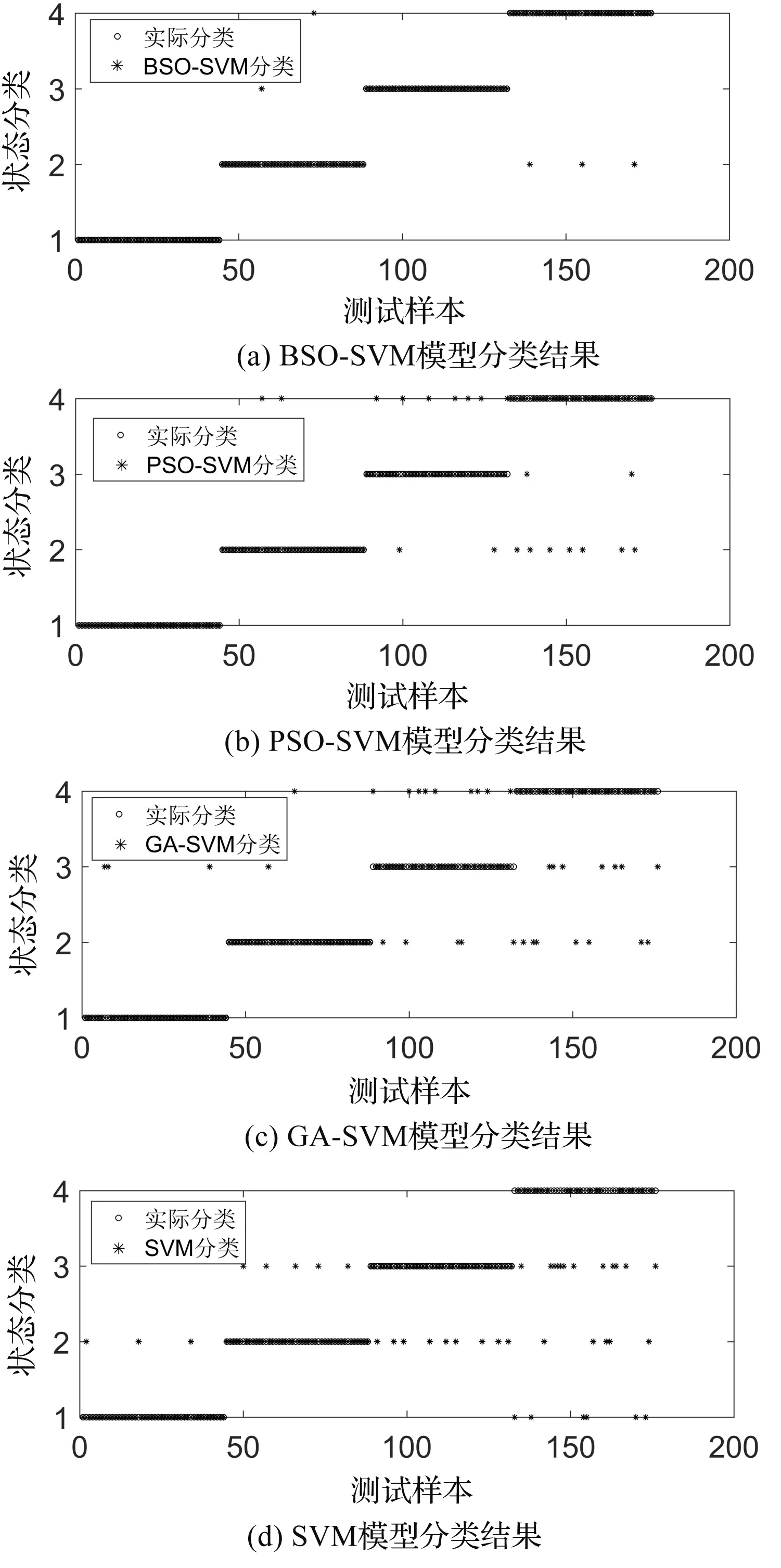
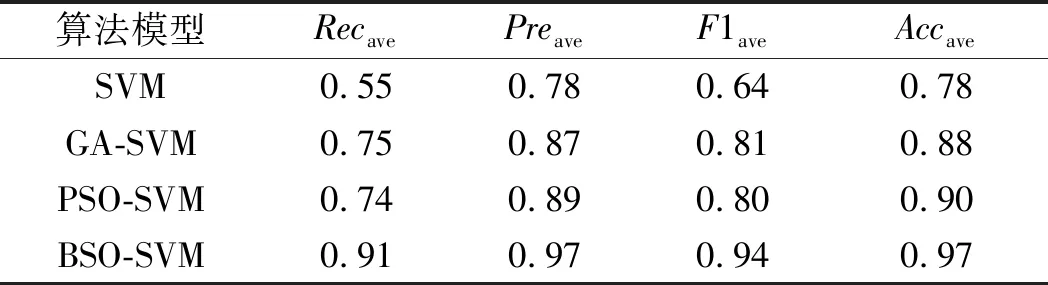
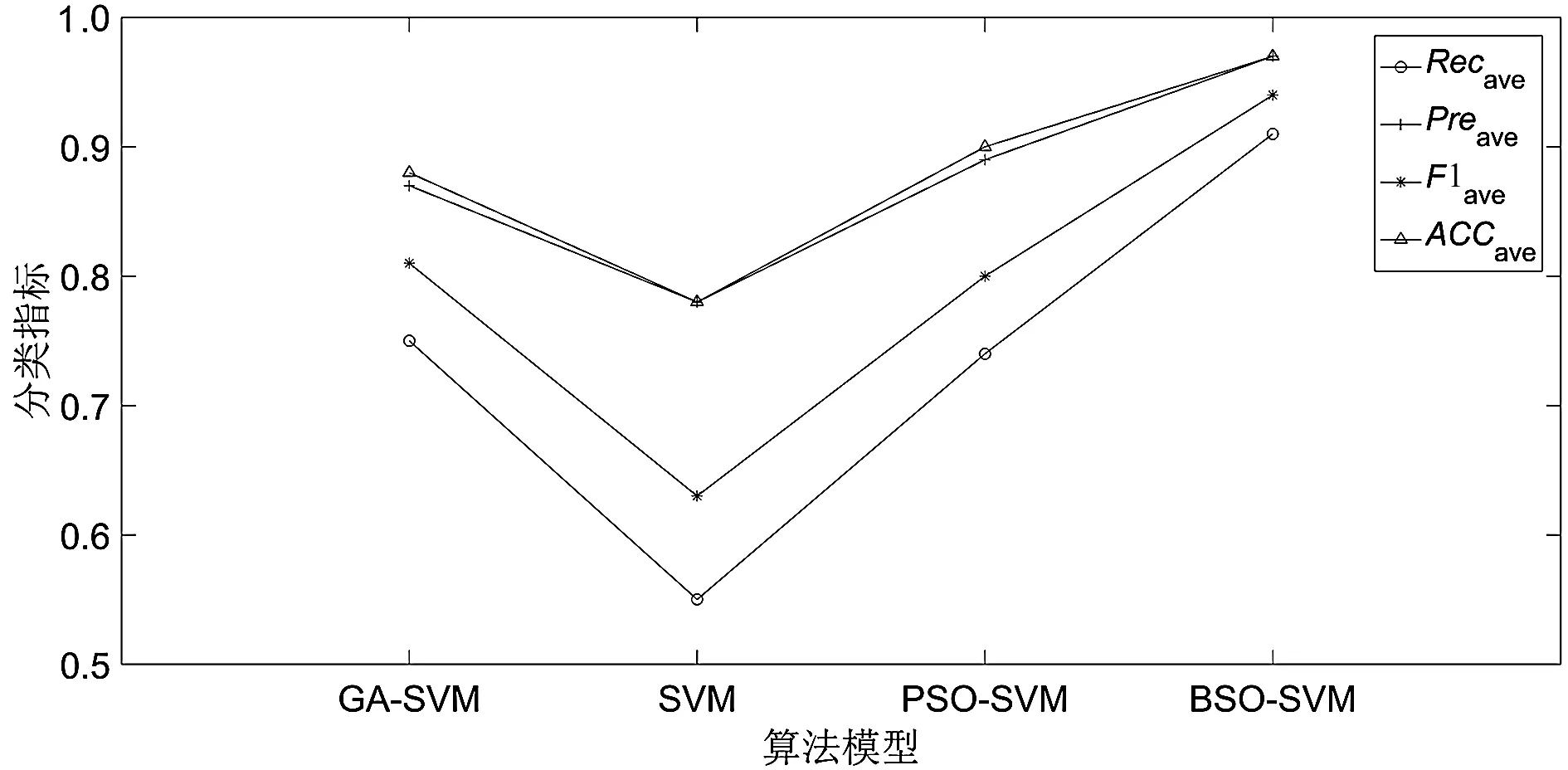
3.3 结果分析

3.4 模型抗干扰能力测试
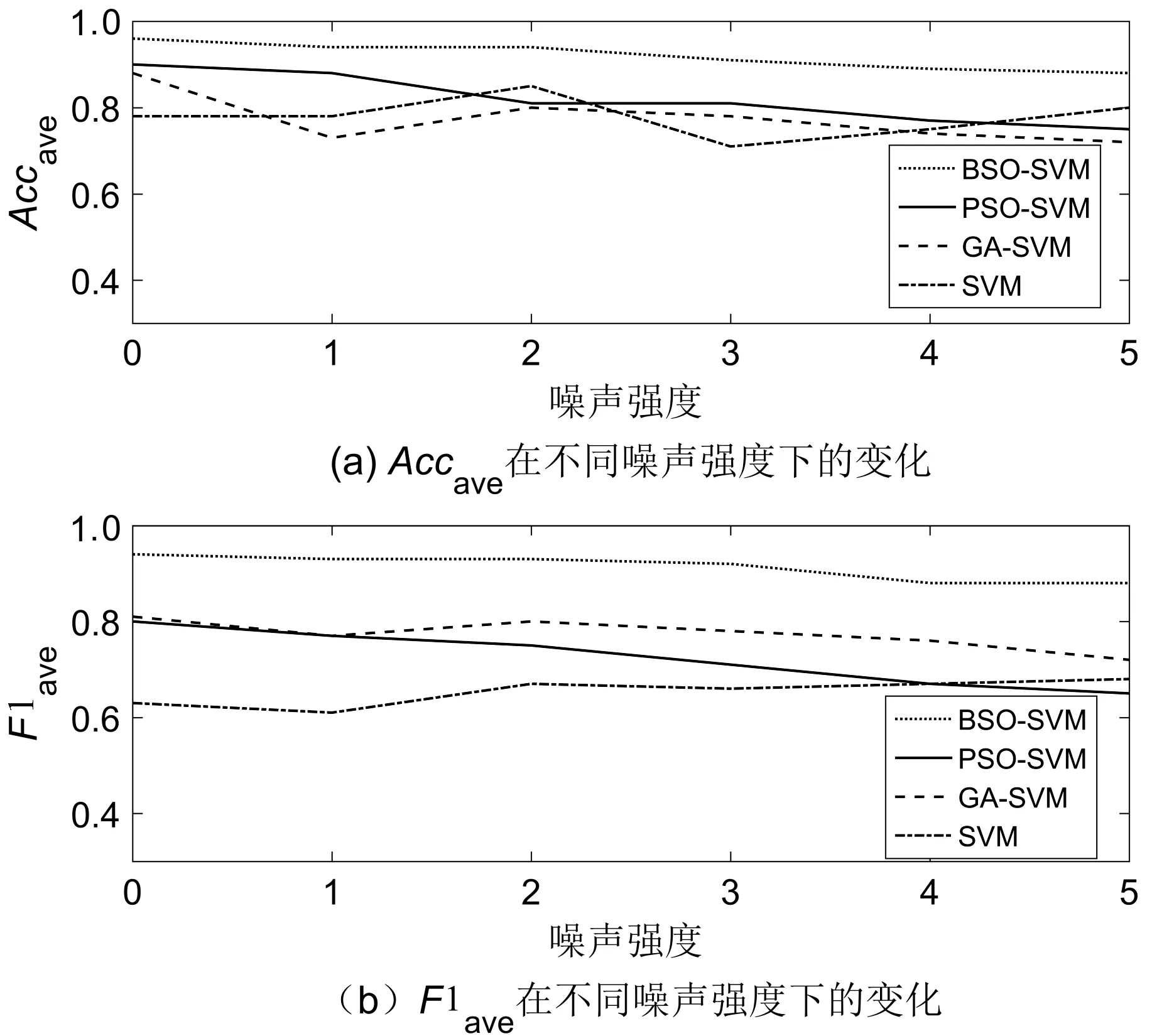
4 结束语

