拒绝服务攻击下的多输入多输出非线性系统无模型自适应控制

赵栩杨,卜旭辉,余 威,游东亚

(河南理工大学电气工程与自动化学院,河南焦作 454000)

1 引言

近年来,工业生产规模越来越大,工艺过程纷繁复杂,建立被控系统的精确模型愈发困难.与此同时信息技术的飞速发展使得工业过程中大量的过程数据被存储,这些数据包含了系统的基本信息,因此如何利用这些数据设计独立于系统模型信息的控制器仍然是一个具有挑战性的问题.无模型自适应控制是一种典型的数据驱动控制方法,它不依赖系统的模型信息,仅利用系统的输入输出(I/O)数据实现控制器的自适应设计[1].经过20多年的发展,无模型自适应控制已经取得了丰富的理论成果[2-5],并且在很多控制系统中得到了应用,如快速路交通、机器人系统、智能超车系统、微电网等.

另一方面,网络控制系统(network control system,NCS)以其传输效率高、安装灵活、数据共享等特点,被广泛应用于智能交通、智能电网、工业过程控制等诸多实际控制系统中.但是由于网络自身的物理局限性,在控制系统中引入网络可能会发生[6-8]:通讯延迟、数据丢失、信道衰落、网络攻击等.文献[9-11]分别讨论了存在通信延迟、信道衰落等无模型自适应控制问题.

需要说明的是,网络攻击是网络控制系统中的另一个问题.网络攻击可以分为3种主要类型[12-14]:拒绝服务(denial of service,DoS)攻击、欺骗攻击和重放攻击.DoS攻击是最常见和最容易的攻击形式之一,其目的是试图阻止各种物理组件之间的通信,从而降低系统性能,甚至使系统不稳定.对网络攻击下的控制问题已有一些研究成果,文献[15-16]针对单输入连续线性系统研究了周期性脉宽调制DoS攻击下的控制问题,并设计了一种弹性控制律来更新控制器以抵抗攻击.在此基础上,文献[17]考虑DoS攻击下的非线性单输入单输出系统的影响,并对系统设计弹性状态观测器.但是实际的控制系统一般为多输入多输出(multiple input and multiple output,MIMO)系统,因此对于MIMO系统的研究是有必要的.对于多输入系统,文献[18-19]考虑系统遭受周期性DoS攻击下的远程控制问题,通过设计合理的控制算法,并且给出系统的稳定条件和触发条件.文献[20]中研究了DoS下的网络控制系统的H∞控制,设置了事件触发条件,以节省网络资源.

以上的研究都是基于系统模型已知而建立的问题,系统的控制取决于系统的模型信息.而对于模型未知或难以建模的复杂控制系统网络攻击问题还没有研究.因此,本文主要研究周期性DoS干扰攻击下的无模型自适应控制问题.由于网络攻击建模通常有周期性网络攻击和持续性网络攻击.本文选择周期性DoS攻击,从能量的角度看,攻击者在结束攻击后进入休眠期进行能量补充,更符合能量准则.而且周期性DoS攻击拥有恒定的周期和占空比,以提高攻击效率,从而周期性DoS攻击的情况更加贴近实际.

本文的主要目的是解决MIMO非线性系统在网络环境下遭受恶意DoS攻击时的无模型自适应控制问题.首先针对周期性DoS攻击进行建模,结合模型设计控制算法,并且通过结合先前时刻的数据信息设计一种补偿算法来消除DoS干扰攻击和随机丢包的影响,使得系统可以更好更快的达到期望输出.最后,仿真结果验证了算法的有效性.本文的主要贡献如下:

1) 在控制系统模型未知的情况下,设计控制算法,解决了存在DoS攻击时未知非线性系统的控制问题;

2) 针对DoS攻击造成的影响,提出了补偿算法,在保证网络控制系统稳定的前提下,可以补偿DoS攻击对控制系统造成的影响,加快控制系统的收敛速度;

3) 本文不仅考虑网络攻击现象,而且还考虑了攻击者处于休眠期间控制系统由于网络带宽限制而发生的随机丢包现象,研究更有一般意义.

2 问题描述

考虑MIMO非线性离散时间系统

其中:u(k)∈Rm,y(k)∈Rm分别是k时刻系统的输入和输出;ny,nu是两个未知的正整数,m是一个已知的整数,f(·)∈Rm是非线性未知函数.

系统(1)满足如下两个假设:

假设1除有限时刻外,f(·)相对于控制输入u(k)的偏导数是连续的.

假设2除有限时刻外,控制系统(1)满足广义Lipschitz条件,即对任意时刻k满足

其中:‖·‖表示欧氏范数,Δy(k+1)=y(k+1)-y(k),Δu(k)=u(k)-u(k-1),b>0是一个常数.

注1假设1是对非线性系统设计的一种典型约束条件.假设2是系统输出针对系统输入变化率的一种反映,从能量的角度来看,如果输入能量的变化是有限的,那么输出能量的变化不可能是无限的.许多实际的控制系统都满足此类假设,例如液位控制系统、压力控制系统等.

基于以上两个假设,给出了下面的定理1.

定理1[21]对于满足假设1和假设2的非线性系统(1),且对所有的k有‖Δu(k)‖/=0,一定存在一个被称为伪雅可比矩阵(pseudo Jacobi matrix,PJM)的时变参数Φ(k)∈Rm×m,使得系统(1)可转化成如下数据模型:

其中系统的PJM如下所示:

假设上述MIMO非线性系统在网络环境下运行如图1所示,传感器、控制器、执行器和保持器组成网络控制系统.传感器与控制器之间的测量信道通过无线信道传递信息.假设攻击者对测量信道发动DoS干扰攻击.同时,还考虑由网络内部因素如带宽限制和网络拥塞引起的随机数据包丢失.

图1 DoS干扰攻击下的网络控制系统Fig.1 Network control system under DoS jamming attack

2.1 DoS攻击和随机丢包建模

假设能量有限的DoS攻击者干扰传感器测量中的通信链路,由于能量限制,攻击者只能在给定时间内攻击有限数量的通信信道,此后攻击者停止攻击,切换到休眠期补充能量,为下一阶段攻击做准备,更好的利用能量.本文将上述DoS攻击视为一种周期性攻击,该攻击可以建模为能量受限的周期性DoS干扰攻击模型.攻击者的任意工作周期可表示为k ∈[(n-1)T,nT],攻击者任意工作周期如图2所示.

图2 DoS干扰攻击工作周期示意图Fig.2 Diagram of DoS jamming attack work cycle

在图2中,T为常数,表示攻击者任意一个工作周期的持续时间;n表示攻击者的第n个工作周期;常数toff(toff∈Z+,toff≤T)表示攻击者在任意一个工作周期内的休眠期持续时间.

定义ξ(k)∈{1,2}表示攻击者处于不同时期,

其中:ξ(k)=1表示攻击者处于第n个休眠期,干扰信号断开;ξ(k)=2表示攻击者处于第n个攻击期,干扰信号通过,通信受阻.

由于无线信道本身的特点,如带宽限制和网络拥塞,数据包在传输过程中会随机丢失.假设丢包现象在休眠期仍然发生,在数据包丢失和DoS干扰攻击下,数据包传输的成功率应该遵循伯努利分布.

定义β(k)表示在周期性DoS干扰攻击下,k时刻的数据包是否传输成功.

注2在以往的研究中,只要网络遭受攻击,数据就传输失败,本文考虑的是在DoS干扰攻击期间数据有传输成功的概率,但是低于休眠期的传输成功率.

2.2 控制算法设计

在本节,将设计一种控制算法,在现有无模型自适应控制算法基础上,考虑DoS干扰攻击和随机丢包的影响,结合第2.1节对DoS干扰攻击建立的模型,针对MIMO系统设计新的控制算法,用于削弱周期性DoS干扰攻击的影响.结合式(4)-(5)在DoS干扰攻击下MIMO非线性离散系统(1)可以表示为

注3将λ引入控制算法(12)中,是用来限制控制输入的变化Δu(k),因此选取合适的λ可以用来保证控制输入信号具有一定的平滑性,并能获得较好的控制性能.

3 主要结果

由于系统在随机丢包和DoS干扰攻击下会发生数据传输失败,数据传输成功率βξ(k)(k)引入系统,使得系统(1)转化为随机系统,从而传统的分析方法不能适用于DoS干扰攻击和随机丢包下的控制系统稳定性分析.因此在本节中,在数学期望意义下对系统的稳定性进行分析.在进行稳定性分析前先介绍以下引理和假设.

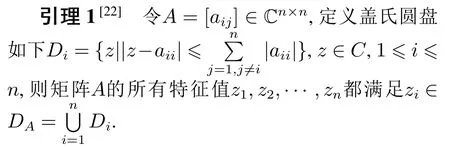
假设3系统的Φ(k)是满足如下条件的对角占优矩阵,即满足|φji(k)|≤b1,b2≤|φii(k)|≤αb2,i,j=1,···,m,i/=j,且Φ(k)中所有元素的符号对任何时刻k保持不变.

注4假设3是对闭环数据输入输出关系的假设,对于MIMO非线性系统,由于系统模型未知,仅有系统当前时刻之前的I/O数据,系统I/O数据关系的对角占优条件可能是表示系统耦合的最终选择.严格来说,如果数据量足够丰富,假设3是可以验证的.

定理2考虑在DoS干扰攻击和发生随机丢包下的非线性离散时间MIMO系统(1),在假设1和假设2满足的条件下,当yd(k+1)=yd=const和输出数据不完全丢失时,存在一个正数λmin>0,使得当λ≥λmin时有:系统跟踪误差序列是收敛的,且(k+1)-yd‖v=0,其中‖(·)‖v是(·)的相容范数.

证定理证明有两个部分,如下所示.

参考系统与控制理论线性代数知识[23],矩阵谱半径结论可知,存在一个任意小的正数ε1,并且对式(20)两端取期望使得

其中:s(A)是矩阵的谱半径,‖A‖v是矩阵A的相容范数,M1是一个大于零的正数.令d2=1-ρM1+ε1.由式(20)-(21)可得

由式(22)可知e(k)有界,由定理2可知yd是给定的常向量,因此可得y(k)输出的有界性.从而可以得出MIMO-MFAC系统的有界输入输出,至此定理2证明结束.

注5由定理1可知所设计的算法在DoS干扰攻击时系统还可以保持良好的稳定性,但考虑到MIMO系统在DoS干扰攻击下并不是所有的输出结果都会传输失败,在遭受恶意DoS干扰攻击时,会对系统稳定性带来一定的影响,因此设计以下的补偿算法来抵消这种负面影响.

4 补偿算法

4.1 控制器设计

由于多输入多输出系统遭受DoS干扰攻击时,系统的输出信号不会全部传输失败,因此设计以下的补偿算法对系统输出进行补偿:

与算法(12)相比补偿算法(26)利用了来自先前时刻的更多信息,采用了预测算法,利用先前时刻的数据对其进行估计,使控制性能预期更好.

4.2 收敛性分析

定理3若非线性非仿射系统(1)在遭受DoS干扰攻击时,在假设1和假设2满足的条件下,当yd(k+1)=yd=const和输出数据不完全丢失时,存在一个正数λmin>0,使得当λ≥λmin时,所提出的补偿算法(25)-(26)保证:

则上式意味着在DoS干扰攻击下输出信号不完全传输失败的情况下,所提出的补偿算法可以保证系统输出误差有界且收敛.

注6DoS干扰攻击下MFAC算法的误差收敛率为

通过对比在发生DoS干扰攻击和随机丢包下不带补偿的MFAC算法的误差收敛率和带有补偿的MFAC算法的误差收敛率,可得出带有补偿的MFAC算法的收敛速度更快,更快的达到期望轨迹输出.在仿真验证中也可得出.

5 仿真示例

1) 数值仿真.

考虑如下MIMO离散时间非线性系统:

假设攻击者一个工作周期持续时间是T=100,每个工作周期的休眠期持续时间toff=50,总的运行时间为1500,因此运行周期为n ∈{1,2,···,15}.假设攻击者处于休眠期系统的数据传输成功率为0.9,处于攻击期系统的数据传输成功率下降为0.6.系统的初始条件为

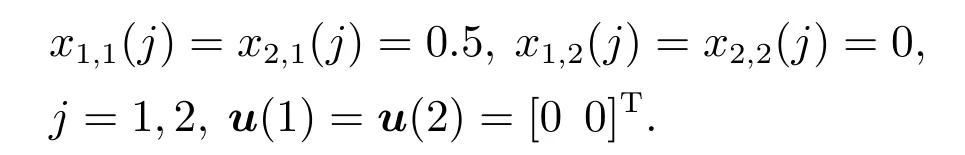
控制器参数初始值为

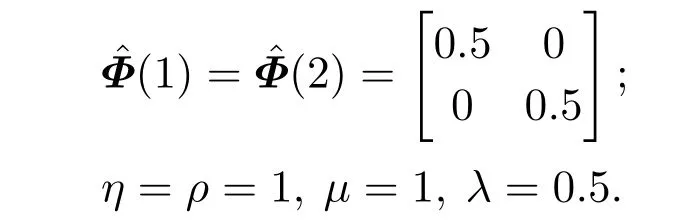
仿真结果如图3所示.

图3 DoS干扰攻击下y1(k)的跟踪性能Fig.3 Tracing performance of y1(k)under DoS attack

系统输出仿真结果如图3-4所示,图中灰色阴影部分表示DoS干扰攻击区间.由图3-4可以看出,在仿真初期,系统输出的超调量和波动范围较大,表示系统受到DoS干扰攻击和随机丢包的影响,发生波动.随着时间的更新,系统输出逐渐达到期望输出.通过与PID控制对比,可以看出本文设计的控制算法加快系统输出收敛速度.

图4 DoS干扰攻击下y2(k)的跟踪性能Fig.4 Tracing performance of y2(k)under DoS attack

系统跟踪误差如图5所示,跟踪误差在初始阶段波动较大,但是随着时间的更新,系统跟踪误差逐渐收敛.图6中数字1-15代表攻击者完整的15个工作周期.火柴棍代表数据传输失败时刻,火柴棍的不同高度表示攻击者处于不同的时期.红色长棍在休眠区间,蓝色短棍在攻击区间.显然,在休眠期火柴棍的分布更稀疏,而在攻击期分布更为密集.

图5 跟踪误差Fig.5 Tracking Error

由数值仿真结果可以看出系统在遭受DoS干扰攻击和随机丢包情况下,初始阶段系统输出跟踪性能较差,但随着时刻的更新,所提出的控制算法能够保证闭环系统有良好的跟踪性能,通过补偿算法对系统控制输入的补偿,最终系统可以更好的达到期望输出,误差渐近收敛于0.通过与PID仿真结果对比,不仅验证了算法的有效性而且突出了本文算法的优越性.

2) 逆变器控制系统仿真.

逆变器控制系统如图7所示,由直流电源、逆变桥、LC滤波电路构成,其中,E是直流电源电压,V是逆变桥交流侧电压,iL是滤波电感电流,iR是负载电流,VC是滤波电容电压.数据采集器通过电力线采集数据通过网络控制系统传输,脉冲发生器根据控制输入信号产生适当宽度脉冲,驱动逆变桥动作,从而获得期望的交流输出电压.

图7 逆变器控制系统结构Fig.7 Inverter control system structures

逆变器系统可表述为

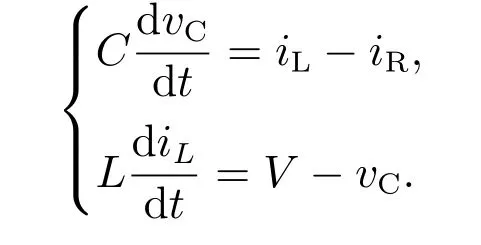
将电容电压vc和电感电流iL作为输出变量y=[vCiL],逆变器交流侧电压和负载电流作为输入变量u=[V iR].仿真中逆变器直流侧电压E=400 V,滤波电感L=2.5 mH,滤波电容C=60µF,参考电压vr=220sin(100πk).逆变控制系统期望输出如下

假设攻击者一个工作周期持续时间为T=50,休眠持续时间toff=25,总的运行时间为600,即运行周期n ∈{1,2,···,12}.假设攻击者处于休眠期系统的数据传输成功率为0.9,处于攻击期间系统的数据传输成功率下降为0.6.MFAC算法控制器参数设置如下η=0.5,ρ=0.5,µ=1,λ=0.01.PJM估计值的初值为

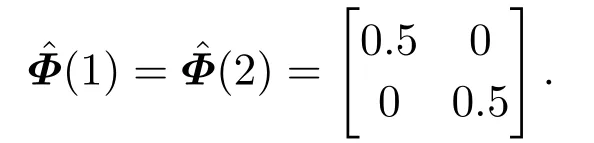
图8-11表示逆变器控制系统仿真结果.如图8所示,本文设计的控制算法在发生DoS干扰攻击和随机丢包下可以保持电压稳定输出,而通过补偿算法对控制输入进行补偿,系统的输出电压可以更好的达到期望值.图9是逆变器输出电流波形图,在遭受DoS干扰攻击下电流幅值波动较大,通过与PID对比可知补偿算法可以加快系统的收敛速度.图10是误差跟踪图,系统的跟踪误差曲线图随着时间更新逐渐平稳.图11是DoS干扰攻击下控制系统数据传输失败时刻,红色代表休眠期数据传输失败时刻,蓝色代表攻击期数据传输失败时刻.

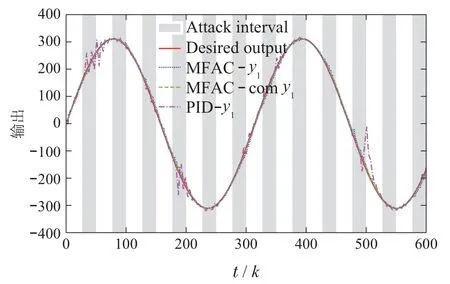
图8 DoS干扰攻击下逆变器输出电压图形Fig.8 Inverter output voltage graph under DoS attack

图9 DoS干扰攻击下逆变器输出电流图形Fig.9 Inverter output current graph under DoS attack

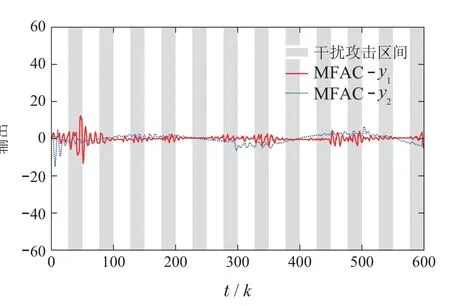
图10 跟踪误差Fig.10 Tracking Error

图11 数据传输失败时刻Fig.11 Time of data transmission failure

仿真结果显示出周期性DoS攻击和数据包丢失会降低系统数据传输成功率,降低系统的稳定性.本文提出的MFAC算法可以有效抵消DoS干扰攻击给跟踪性能带来的负面影响,仿真结果验证了算法的有效性,而且通过与PID算法仿真结果的对比,更好的展现出了算法的优越性.

6 结论与展望

本文针对MIMO非线性系统,提出一种基于周期性DoS干扰攻击和随机丢包的无模型自适应控制算法.首先通过引入伯努利分布对周期性DoS干扰攻击和随机丢包进行建模,结合MIMO非线性系统设计控制算法,其次通过数学推导分析了算法的收敛性,最后仿真结果表明所提出的控制算法在DoS干扰攻击下仍然可以保证系统的稳定性,并且补偿算法可以减轻DoS 攻击对控制系统的影响,加快系统收敛速度,此外该算法是数据驱动的不依赖系统的模型信息,仅用系统I/O数据.缺点是在DoS攻击下数据更新失败时系统仍然会传输历史数据,从而造成网络资源的浪费.如何在DoS干扰攻击环境下针对MIMO非线性系统设计事件触发机制,减少系统通信资源的浪费,这将是以后研究重点.