事件触发下马尔可夫跳跃神经网络的随机同步

陆丹旎 ,童东兵 ,陈巧玉 ,周武能

(1.上海工程技术大学电子电气工程学院,上海 201620;2.东华大学信息科学与技术学院,上海 200051)

1 引言

近十年来,由于神经网络在图像处理、模式识别、信号处理、联想记忆和组合优化等领域的成功应用,神经网络的动态特性得到了广泛的研究[1-2].同步问题是神经网络研究中的一个有趣且有意义的问题,受到了极大的关注.当误差系统的状态最终接近零时,主系统和从系统就实现了同步.迄今为止,神经网络同步有着丰硕的研究成果,已研究的同步类型有,自适应同步[3]、相位同步[4]、全局同步[5]、H∞同步[6]和随机同步[7]等.

随着对神经网络分析研究的深入,系统干扰经常被考虑在神经网络中,例如文献[8]中的时滞和文献[9]中的随机噪声.在控制系统中,时滞会造成系统不稳定或引起振荡.这些现象都不利于神经网络的实际应用.在文献[10]中,针对具有时变时滞的高阶多智能体系统,利用控制输入约束和跟踪误差约束设计了编队跟踪协议,保证了鲁棒H∞干扰抑制性能.在文献[11]中,采用间接方法解决时变时滞和执行器饱和的问题,为广域电力系统设计了一个与时滞相关的抗饱和补偿器,可以增强区域间低频振荡的阻尼.

此外,当一个系统的结构发生突变时,其动力学可以用连续时间马尔可夫链驱动的马尔可夫跳跃系统来表示.由于系统的状态值取连续值,而跳跃参数取离散值,因此将该系统视为混合系统的一个特例.文献[12-13]及其参考文献对带有马尔可夫跳跃参数的系统进行了深入的研究.

在目前的触发控制研究中,控制信号大多采用周期采样或者时间触发采样的方式来控制信息的传输.这两类控制方法可能会将不必要的控制信号传输至系统.然而,基于事件触发机制的控制策略可以充分利用有限的带宽资源实现较高的控制需求.在事件触发机制下,只有当采样数据满足某个预先设定的触发条件时才会进行数据传输.利用这种机制,能够极大地降低数据的传输量,减轻网络带宽的传输压力.在文献[14]中,对于不确定离散系统,构建了一种沿迭代轴的事件触发机制,能够减少迭代过程中控制信号的更新次数.

基于以上讨论,本文主要研究了在事件触发机制下带有马尔可夫跳跃参数的主从系统随机同步的问题.本文的创新如下:

1) 构建了带有马尔可夫跳跃参数、时变时滞和随机噪声的神经网络模型.此模型更具有普遍性,并且适用于多种不同的系统;

2) 通过事件触发机制实现了主从系统的同步.与采样数据控制方法相比,不仅能使主从系统快速同步,而且可以减少控制信号的传输次数、减轻网络传输压力;

3) 通过构建Lyapunov泛函的方法,得到了使误差系统稳定的充分条件.可以解决马尔可夫跳跃参数、时变时滞和随机噪声同时存在的问题.

2 问题描述

设{r(t),t≥0}是概率空间上的右连续马尔可夫链,取有限状态空间S={1,2,···,S},其转移率矩阵Γ=(γij)N×N由以下公式给出:

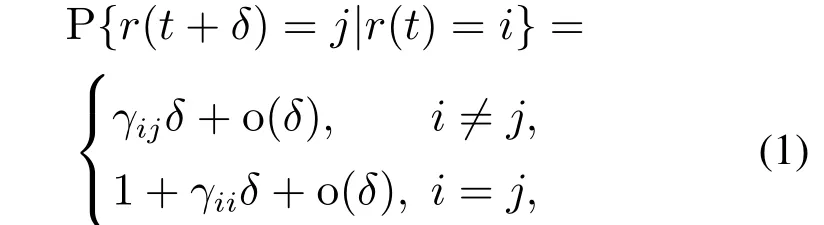
其中:δ >0.γij≥0是从i到j的传输速率,当i/j时

考虑如下的主从系统的动态模型:

其中:r(t)是马尔可夫链,x(t)∈Rn表示主系统(3)的状态向量,同时y(t)∈Rn表示从系统(4)的状态向量.f(x(t))和f(y(t))是神经元激活函数.A(r(t))是一个对角矩阵.B(r(t))表示连接权矩阵,C(r(t))表示时滞连接权矩阵.σ:Rn×Rn×S→Rn×m代表随机噪声强度矩阵.ω(t)是定义在完备概率空间的标准布朗运动.ζ(t)是时变时滞并且满足

进一步记ζ12=ζ2-ζ1.u(t)∈Rn表示控制器.

假设1对于任意x,y ∈R,式(3)和 式(4)中 的神经元激活函数f(x(t))和f(y(t))是有界的,并且满足以下Lipschitz条件

其中H ∈Rn×n是已知的常数矩阵.

将同步误差信号定义为e(t)=y(t)-x(t).因此,误差系统可以表示为

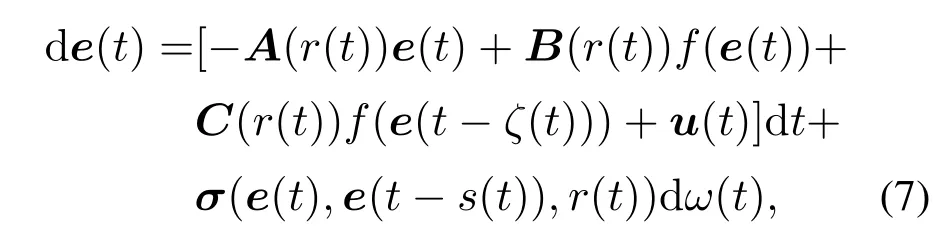
其中f(e(t))=f(y(t))-f(x(t))=f(x(t)+e(t))-f(x(t)).由假设1可知,转化后的神经元激活函数f(e(t))满足f(e(t))≤He(t).

设误差系统在离散时刻tk(k ∈N)的采样状态为e(tk)=y(tk)-x(tk).采样状态e(tk)是否能进行传输由传输误差和状态误差决定.传输误差是指当前系统状态与上一个采样状态之间的误差e(t)-e(tk),状态误差是指当前系统状态到平衡点的误差e(tk).只有当传输误差和状态误差满足触发条件时,数据才能够被传输到控制器中.当误差系统的采样状态e(tk)进行传输时,为了下一个采样状态e(tk+1)的确定,还需要将采样状态e(tk)储存在控制器中.直到下一个采样状态满足触发条件时,控制器数据才更新.假设对于任意整数k >0,都有tk+1-tk≤h,其中h是采样间隔的上限.本文的事件触发机制设计如下:

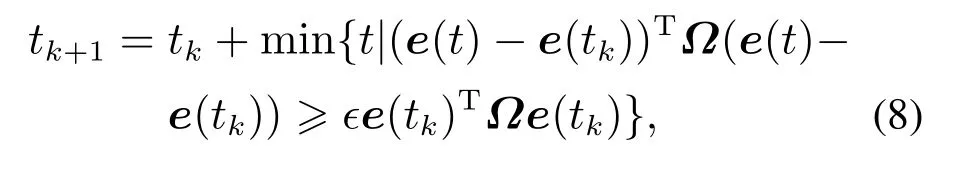
其中:矩阵Ω >0,ϵ ∈[0,1)是触发参数,e(tk)只有在满足不等式(8)的情况下才会被传输.从系统中的控制器可以被设计为如下形式:

其中K(r(t))是一个控制器增益.

将误差系统(7)中的控制器用式(9)代替,系统(7)可以被重新写为

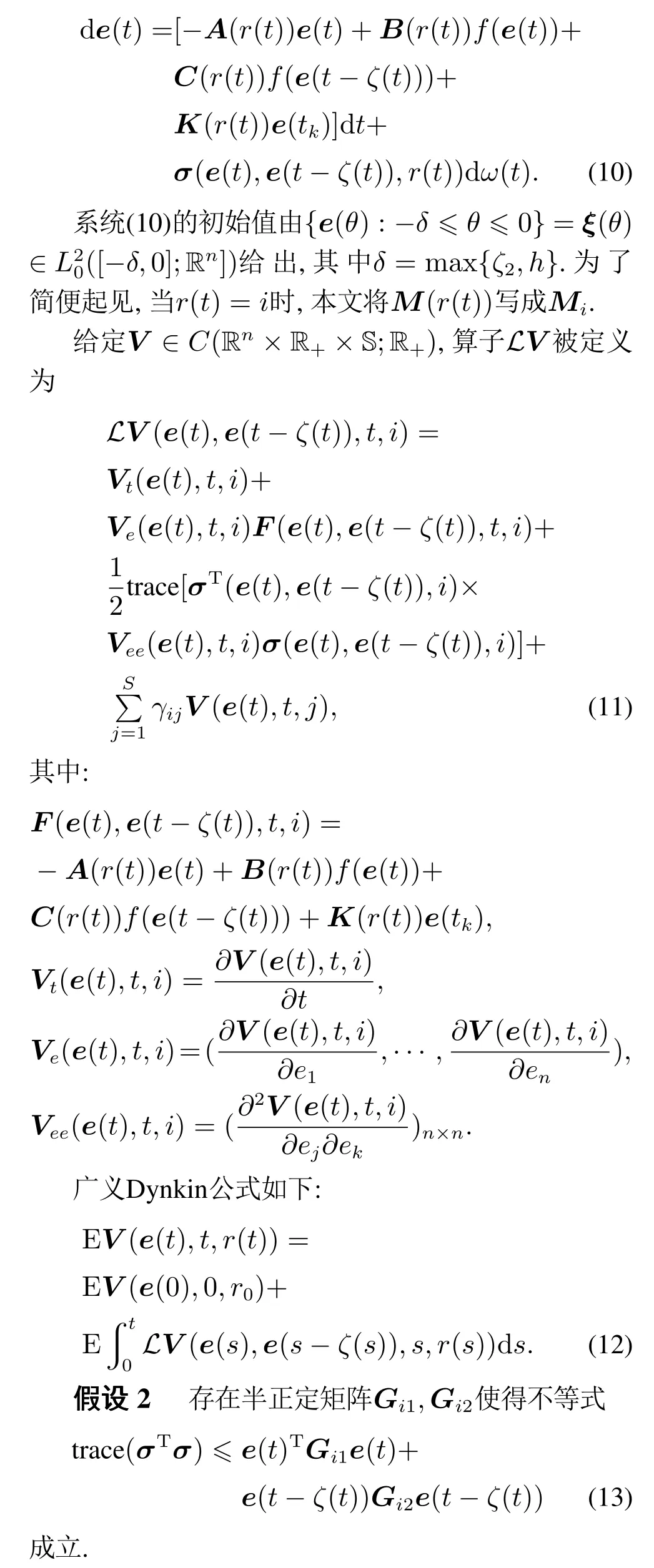
系统(3)和系统(4)随机同步的定义如下.

定义1[15]如果误差系统(10),对于定义在区间[-δ,0]和r(0)∈S上的初始条件e(t)=ξ(t)满足

则误差系统(10)是随机稳定的,也就是说,主系统(3)和从系统(4)是随机同步的.

为了分析误差系统的稳定性,总结了以下必要的引理.

3 主要结论

本节根据Lyapunov泛函,对于系统(3)和系统(4)所描述的马尔可夫跳跃主从神经网络,设计了基于事件触发的同步控制器,并证明了主从系统的同步.

定理1给定一个标量γ,如果存在常数ε1>0,ε2>0,正定矩阵Pi >0,Ki >0,Q1>0,Q2>0,Q3>0,W1>0,W2>0,W3>0,W4>0,满足如下不等式:

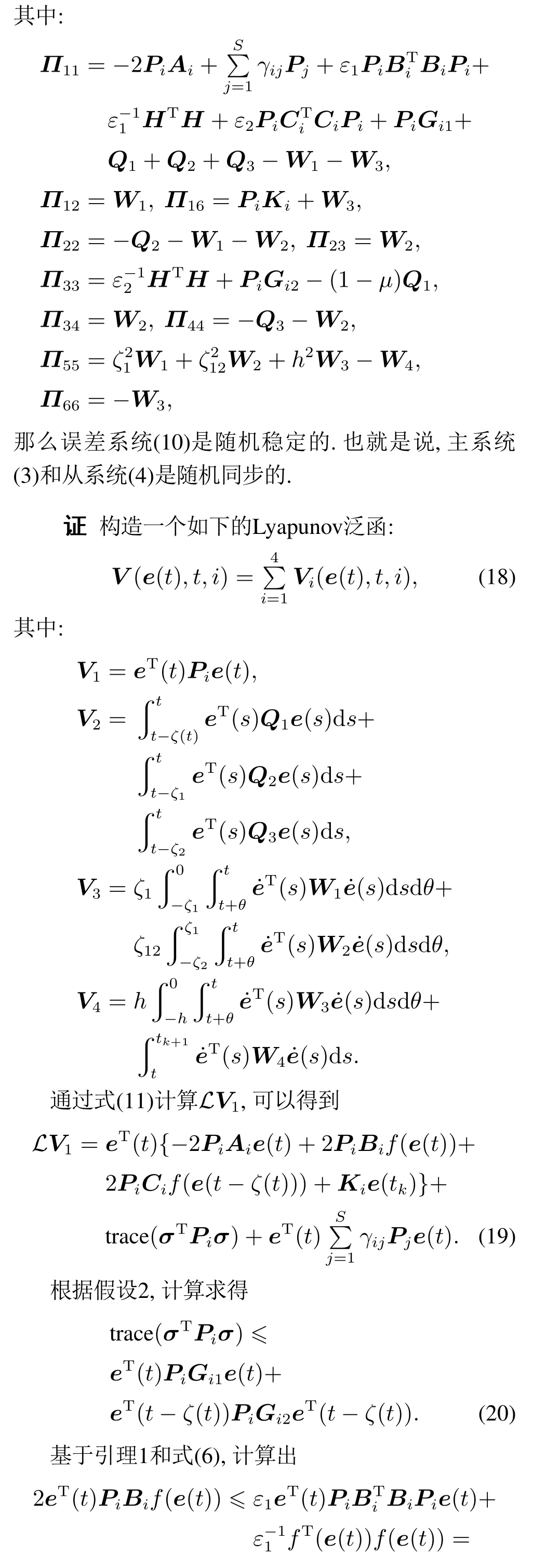
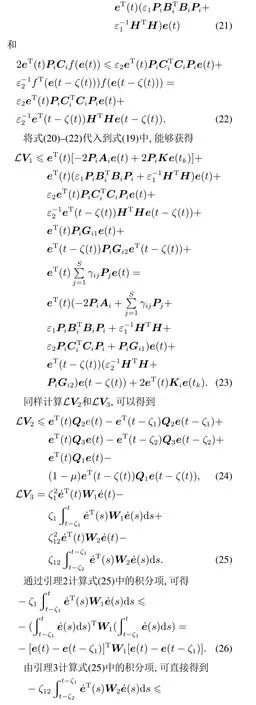
注1此研究中,引理3被用于处理式(25)中积分项.在文献[19]中,Jensen不等式被用于处理积分项

在计算前需要匹配积分区间的长度,并且需要定义新的自由加权矩阵G0.然而,引理3在不需要定义自由加权矩阵的情况下给出了一个改进的计算方法.将引理3和Jensen不等式结合使用,在简化计算的同时,证明中所有积分项都可以被计算.

4 仿真

为了验证本文所提出的方法的有效性,给出如下的仿真.

通过验证,以上的结果满足定理1所给出的条件.系统仿真图如图1-5所示.图1是由转移率矩阵Γ生成的马尔可夫链.图2是随机噪声.图3是事件触发机制(8)的触发时间间隔.其中,横坐标表示触发时刻,纵坐标表示两个相邻触发时刻的时间间隔.纵坐标的数值越大,两个相邻触发时刻之间的时间间隔也就越长,即控制信号更新的时间也就越长.图4是误差系统的状态轨迹.从中可以看出随着时间的增加,系统(10)的状态轨迹趋于0.这说明了误差系统是稳定的,也就是说,主系统(3)和从系统(4)是同步的.图5是控制输入的信号.

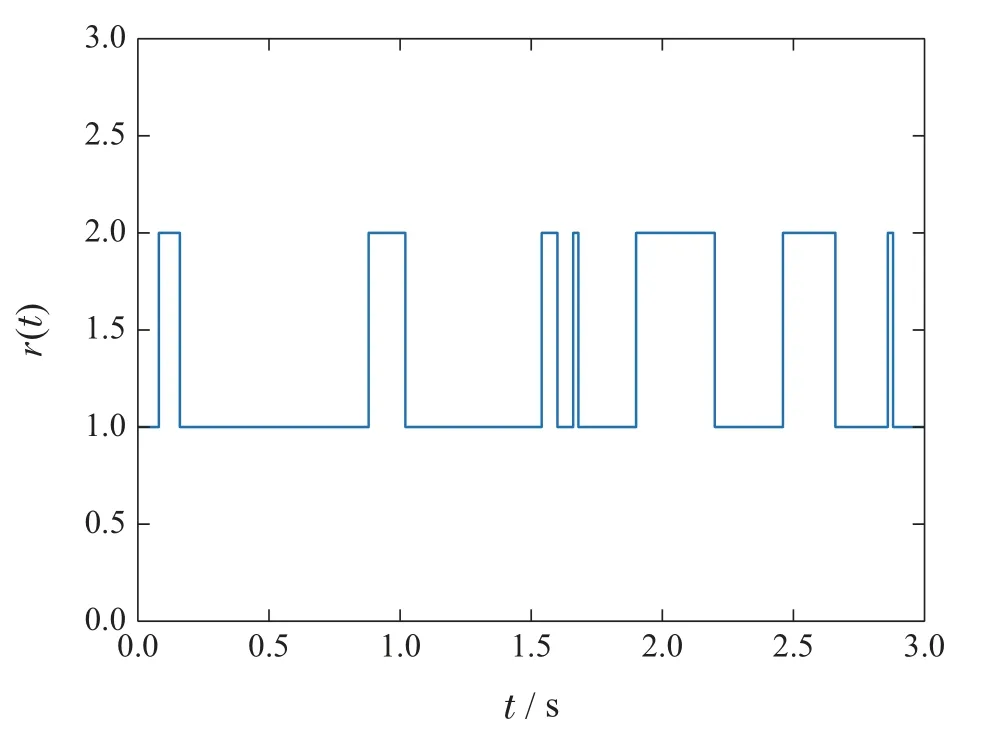
图1 马尔可夫链Fig.1 Markov chain

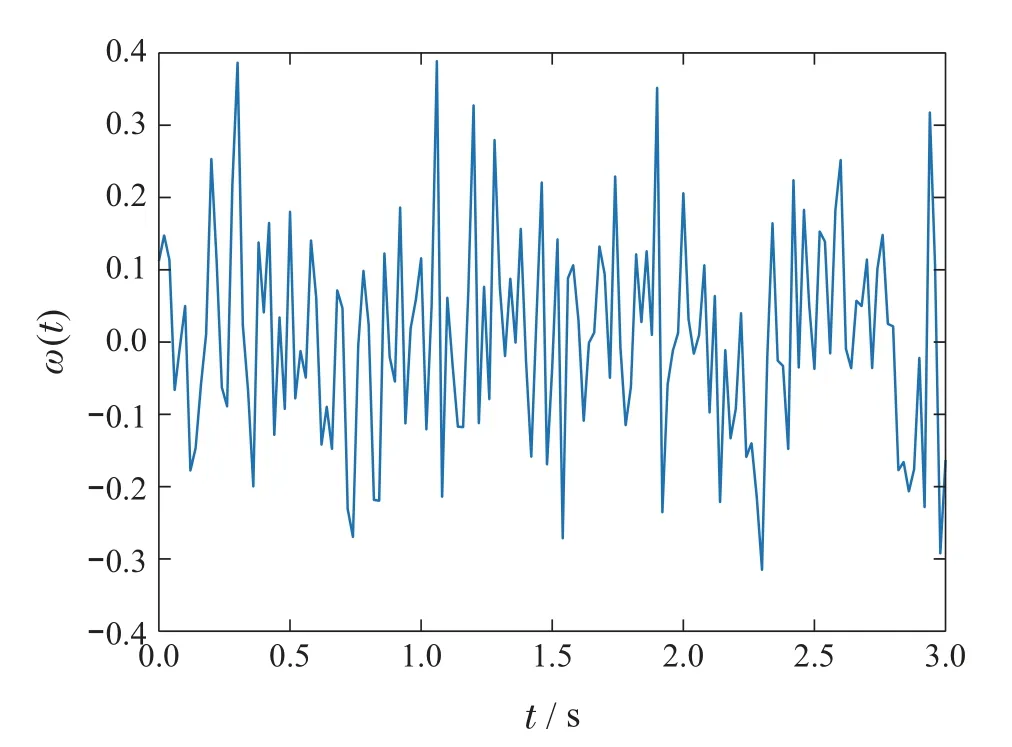
图2 随机噪声Fig.2 Random noises

图3 事件触发控制的信号释放瞬间Fig.3 The release instant of event-triggered control

图4 误差系统状态轨迹Fig.4 The state trajectory of the error system

图5 控制输入Fig.5 Control input

注2根据图3,在条件(8)的事件触发控制下,信号传输次数为94次.在相同时间内,使用文献[20]中的采样数据控制作为信号控制,选择最大传输间隔为0.02 s,信号传输次数为150次.根据图5,本文控制输入的信号曲线相比文献[20]波动更少.显然,与采样数据控制相比,条件(8)可以节省更多的通信资源.

5 结论

本文对一类带有马尔可夫跳跃参数的神经网络随机同步问题进行了研究.并且根据Lyapunov稳定理论,给出了能够使主从系统达到随机同步的充分条件,同时也得到了基于事件触发机制的同步控制器的设计方法.此外,系统中考虑到了时变时滞、马尔可夫跳跃参数和随机噪声的影响,使得系统更具有普遍性.通过事件触发机制进行信号传输控制,使得在实现主从系统同步的过程中,可以有效降低数据传输量,提高网络带宽利用率.最后,给出一个数值例子,通过MATLAB仿真,与采样数据控制相对比,展示了所提出方法的有效性.