多步积累奖励的双重时序Q网络算法

朱 威,谯先锋,陈艺楷,何德峰

(浙江工业大学信息工程学院,浙江杭州 310023)

1 引言

随着无人驾驶汽车产业的不断发展,其核心的控制决策技术受到了越来越多的关注.现有无人驾驶控制决策的方法主要分为两大类[1]:一类是基于规则的控制决策,另一类是基于学习的控制决策.基于规则的控制决策主要是根据交通规则、行驶规则、先验知识等建立一个行为规则库,然后根据无人驾驶汽车的自身行驶状况和当前环境信息,对车辆的状态进行划分,最后根据行为规则库确定车辆的驾驶动作.基于学习的控制决策主要是由数据进行驱动,系统自学习采集到的环境信息和自身状态,根据不同的学习方法和网络结构建立不同行为规则库,然后将当前环境信息和自身状态作为输入,确定车辆的驾驶动作.

Talebpour等[2]提出的有限状态机法,是最具代表性的基于规则的控制决策算法.因其具备良好的实用性和稳定性,而广泛应用于无人驾驶的控制决策系统中.但由于很难建立能够覆盖所有场景的行为规则库,导致该类方法无法处理复杂的场景[3].近年来,深度学习(deep learning,DL)作为机器学习的一个重要的研究领域,得到了巨大的发展,为强化学习(reinforcement learning,RL)提供了强有力的支撑,解决了许多之前难以解决的问题.深度强化学习(deep reinforcement learning,DRL)是DL和RL的结合物,具备二者的优点,因此DRL作为基于学习的无人驾驶方案,逐渐成为解决无人驾驶控制决策的主流算法.

在现有的研究工作中,基于规则的有限状态机法不能处理复杂的驾驶环境.Bojarski等[4]提出了一种基于深度学习的决策控制算法,通过省略中间的决策部分,直接建立“状态”-“动作”的映射关系,实现了无人驾驶汽车的“端对端”控制.但这种方法需要大量含有标签的训练数据,而这对于大部分研究人员来说较难获得.Chi等[5]提出了一种基于模仿学习(imitate learning,IL)的方法,让用户示教期望的驾驶风格,并结合基于特征的逆强化学习来找到最适合人类驾驶风格的参数.但这种方法对于示教人员难以演示的突发情况和危险情况难以学习,而这些状况正是驾驶过程中最重要的部分.DRL算法是通过智能体与外界环境交互的结果来学习驾驶规则,但为了使其能适应现实环境,仍然需要解决的核心问题是如何使智能体能够以更高的效率处理交互得到的数据[6-7].为了解决DRL算法处理数据效率低的问题,DeepMind[8]提出了优先经验回放机制(prioritized experience replay,PER),通过更频繁地回放重要的经验组,来减少训练步数,提高数据的利用率.Deisenroth等[9]提出了非参数转换高斯模型,通过减少模型错误的影响提高数据效率.Nachum等[10]提出了一种在上级和下级中都使用非策略性经验,以提高分层强化学习的学习效率.

本文针对无人驾驶汽车的控制决策问题,在深度双Q 网络(double deep Q network,DDQN)的基础上,将多步积累奖励策略与时序网络结构相结合,提出了一种基于多步积累奖励的双重时序Q 网络算法(multi-step accumulation reward double time-series Q network,MDTQN).首先,为了解决传统强化学习仅利用即时奖励而导致处理数据效率低的问题,以及现有多步即时奖励法不能突显当前奖励重要性和奖励值过大等问题,本文算法设计了一种多步积累奖励方法.其次,考虑到无人驾驶汽车在连续时间内的各个状态与以前时刻的状态有着密切关联,并且状态间存在长期依赖关系,以及具有很强的时序相关性.而传统DRL算法中的卷积神经网络(convolutional neural network,CNN)[11]仅能够对输入数据的局部空间特征进行提取,不能对连续状态进行时序特征的捕获.因此,本文算法设计了一种将CNN和长短期记忆网络(long short-term memory networks,LSTM)[12]相结合的时序网络结构,使其不仅具备了捕获时序特征的能力,而且加强了对局部空间特征提取的能力.

2 相关工作

2.1 Q学习

Q学习是一种无监督强化学习模型,被视为异步动态规划的方法[13].该方法通过与环境进行交互,能够使智能体在马尔可夫域中学习到最优的行为策略,而无需构建域的映射关系,其学习过程与时序差分方法类似,是强化学习中基于价值迭代的算法.Q学习是智能体通过Q值表选择动作与环境交互,获得即时奖励或惩罚,并进入下一个新状态,然后通过即时奖励或惩罚对Q值表进行更新,一直重复迭代,直到Q值表收敛.Q学习算法的核心在于价值函数迭代过程,即:

其中:rt是状态st转移到st+1获得的即时奖励值,α(0<α<1)是学习率,γ(0<γ <1)为折扣因子.

从式(1)可以看出,Q学习算法在进行价值函数迭代时,仅使用了当前状态下获得的即时奖励作为更新条件.但这种方式在处理稀疏奖励时,由于奖励值大多为零,所以对Q值表的更新效率非常低.

传统多步即时奖励学习算法(例如n步Q学习与n步Sarsa)[14],通过自举的方式获得未来多个时刻状态下的奖励值,并将这些奖励共同作用于价值函数的更新,从而提升Q学习的学习性能,以及改善Q学习对数据利用率低的问题.因此,对于n步Q学习的奖励回报函数Gt为

传统多步即时奖励方法虽然能够克服Q学习仅使用即时奖励更新策略所带来的影响,在一定程度上提高了智能体对数据的利用率.但是,该方法在获取多步即时奖励时未进行均值化处理,这可能会导致奖励值过大的问题,进而导致算法不能够收敛;另外,当前状态的即时奖励是对执行该动作好坏最直接的反映,在传统多步即时奖励方法中忽略了其重要性.

2.2 深度Q网络

深度Q网络(deep Q network,DQN)是一种将神经网络和Q-learning相结合的方法[15].传统的Q学习算法使用Q值表的方式记录状态和动作对,在处理状态空间或是动作空间很大的问题时,Q值表占据很大的内存,而且在海量的表格中搜索策略也需要大量的时间.为了解决这个问题,Dong等[16]提出了函数逼近法,通过使用参数化的模型来代替Q值表,并且近似地表示整个状态价值函数或动作价值函数,进而将强化学习推广到更广泛的状态空间和动作空间.由于深度学习理论的快速发展,并且神经网络具备强大的表达能力和自动寻找特征的能力.所以,神经网络已经成为函数近似法中最常见的近似函数.而将神经网络和强化学习相结合,直接将状态作为神经网络的输入,用神经网络计算出所有动作的期望值,并从中选出一个最大值作为输出,或者将状态和动作都作为神经网络的输入,直接输出对应的Q值,这就是DQN.对于DQN在更新网络时,其奖励回报函数为

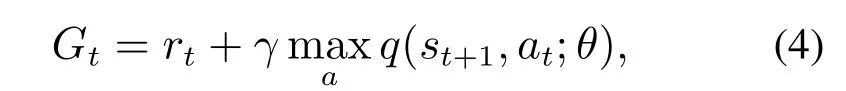
其中:rt是智能体交互得到的即时奖励,θ是神经网络参数.

DQN使用神经网络代替原有的Q值表作为价值函数,解决了不能够处理大规模状态空间或动作空间的问题.但由于DQN使用贪婪策略估计动作价值函数,并且每次选择最大的估计值,所以在学习过程中可能会导致过估计现象.这种过估计可能会产生正面影响,也可能会导致负面结果.如果这种过估计现象没有集中到想要的状态,就会产生不利的价值估计,甚至会导致策略向局部最优估计值靠拢,最终导致整个网络无法收敛.为了解决这个问题,DDQN采用了将动作选择与策略评估分开[17].因此,DDQN使用了两个独立的动作价值估计函数q(0)(·,·)和q(1)(·,·),每次更新动作价值时使用其中一个网络确定动作,用确定的动作和另一个网络来估计回报,从而代替DQN中的由于q(0)(·,·)和q(1)(·,·)是独立进行动作价值估计,所以

因此,在DDQN算法的学习过程中,使用当前动作选择网络q(1)(·,·)计算最大价值函数的动作amax:

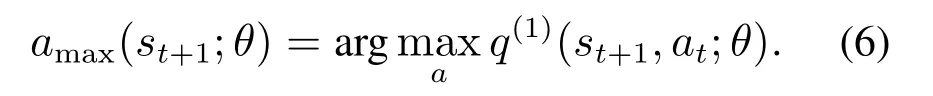
然后,利用最优动作计算出策略更新回报的估计值

最终,根据策略更新回报的估计值Ut,DDQN的价值函数迭代过程为

3 基于多步积累奖励的双重时序Q网络算法

为了解决强化学习算法仅利用单步即时奖励对策略进行更新,而导致智能体对数据利用效率过低的问题,以及传统多步即时奖励法无法有效处理状态中包含大量稀疏奖励,或是奖励值过大、不能突显当前奖励重要性等问题.首先,在本文中设计了一种多步积累奖励方法,该方法对未来多步即时奖励的累加和进行均值化后,与当前即时奖励一起作用于智能体的控制策略,并在奖励函数中突显当前即时奖励的主导影响.然后,为了更好地捕获无人驾驶过程中连续状态之间的时序相关特征,本文算法设计了一种将LSTM和CNN相融合的时序网络结构.

3.1 多步积累奖励方法

本节针对DRL算法仅考虑当前即时奖励对策略更新的影响,以及为了提高DRL算法处理数据的能力,在传统多步即时奖励方法的基础上设计了一种新多步积累奖励方法,该方法改变了传统多步即时奖励方法中的回报函数,采用累加未来多个时刻的传统多步即时奖励作为当前时刻的奖励值.

所设计的新多步积累奖励方法相较于传统多步即时奖励方法能够更好的利用数据,提高了数据的有效性.这是因为在运用传统多步即时奖励方法处理稀疏奖励时,对于缺失项使用零代替,导致智能体缺少该时刻的特征信息.但新多步积累奖励方法融入了更多未来奖励信息,不会因为该时刻的即时奖励为零,而缺少该时刻的状态特征,从而增强数据对智能体的有效性,以及间接提升了智能体对数据的利用效率.

在强化学习中,智能体奖励值的大小将直接影响训练的最终结果.当奖励值过大或是过小时,会导致网络不收敛、训练速度慢、结果不优,或者智能体不能够学到想要的结果.因此,为了避免出现以上问题,本文将对新定义的奖励回报函数进行均值化处理,即奖励回报函数定义为

其中Gt+i为t+i时刻的多步即时奖励,具体如式(2)所示.

虽然在奖励回报函数中增加未来多步积累奖励可以加快智能体的训练速度,以及均值化处理能够有效地避免网络出现不收敛等问题.但智能体与环境交互得到的当前即时奖励是对当前选择动作好坏最直接的反应.因此,应该在回报函数中突显当前时刻下的即时积累奖励的重要性,进而突出当前即时奖励对智能体的影响.所以,最终的奖励回报函数定义为

其中:Gt是传统多步即时奖励,β是当前多步即时奖励对整个奖励回报函数的影响因子.

其中:γ是折扣因子,rt是从状态st转移到st+1时获得的即时奖励值.

在本文中将驾驶决策问题建模为马尔可夫决策过程,因此,系统中的每一个状态都具备马尔可夫性质[18].根据马尔可夫性,当一个随机过程在给定状态以及所有过去状态的情况下,其未来状态的条件概率分布仅依赖于当前状态,又由于智能体的动作选择机制是确定的,所以系统的下一个状态st+1仅与当前状态st有关,而与以前的状态无关.因此,可以简化为

从式(16)可知,当β=1时,新定义的多步积累回报函数与单步回报函数一致,该多步法退回到单步法;当β不等于1时(0<β <1,n>1),多步积累奖励回报函数能够利用长期奖励,提升智能体对数据的利用率.当n=1时,多步积累奖励仅与当前奖励有关,β值仅充当常值系数,对智能体的训练没有影响.因此,在已知策略π和状态st下,采取动作a时的状态价值函数为

其中:a′是下一个动作,s′是当前状态和当前动作根据状态转移概率P得到的下一个状态.因此,新多步法价值函数迭代过程为

对于以上公式中的参数n和β的取值,将在第4节的实验部分进一步讨论说明.

3.2 时序网络结构

在传统DRL算法中,主要使用CNN对输入图像进行状态特征的提取,其中的卷积结构、激活结构、池化结构能够对单一时刻下的状态进行特征空间信息的提取,并通过全连接层来完成从输入状态到输出动作的映射关系.但无人驾驶是一个连续的过程,车辆的每一个动作对后续时刻的状态都有着深远影响,并且车辆采集到的连续状态信息,不仅包含静态空间特征信息,而且在状态之间还存在长期依赖关系.若仅使用CNN作为智能体特征提取的网络结构,智能体将只能够获取当前时刻的局部空间特征信息,而忽略状态间的时序特征信息以及时序相关性.这将使状态间的时序特征丢失,并导致智能体不能够通过上下文信息做出更有效的动作选择,从而严重影响智能体的最终执行效果,并间接减慢了其训练速度.

循环神经网络(recurrent neural network,RNN)是一类以序列数据为输入,在序列的传递方向进行递归,并且所有节点(循环单元)按链式连接的递归神经网络[19].相比于同类型其他神经网络,RNN能够更好的处理数据间的序列信息,提高决策的连续性.由Hochreiter和Schmidhuber[12]提出的LSTM是RNN的一个优秀变种模型,同时继承了大部分RNN模型的特性,非常适合处理与时间序列高度相关的问题,能更真实地表征或模拟人类行为、逻辑发展和神经组织的认知过程.

在本节中,网络结构的设计主要考虑以下3 点:1)能够对输入状态进行局部空间特征的提取;2)能够增强网络对时空综合特征的感知和时序特征的提取;3)网络结构简洁,满足无人驾驶的实时性需求.

根据上述分析,本节设计一种将CNN和LSTM相融合的时序网络结构,具体如图1所示.其中最外层是大小为128×128×3(输入状态大小)的输入层.接着为3个Conv2d卷积层,并对其每一个输出采用ReLU激活函数.其中,第1个Conv2d使用了32个8×8卷积核,步长为4;第2个Conv2d使用了64个4×4卷积核,步长为3;最后一个使用了32个3×3卷积核,步长为1.然后是外层有TimeDistributed包装的Flatten层.接着使用了512个单元的LSTM层,并对其输出采用了tanh激活函数.最后是两层Dense,分别采用128个单元和9个单元,作为动作期望值的输出.

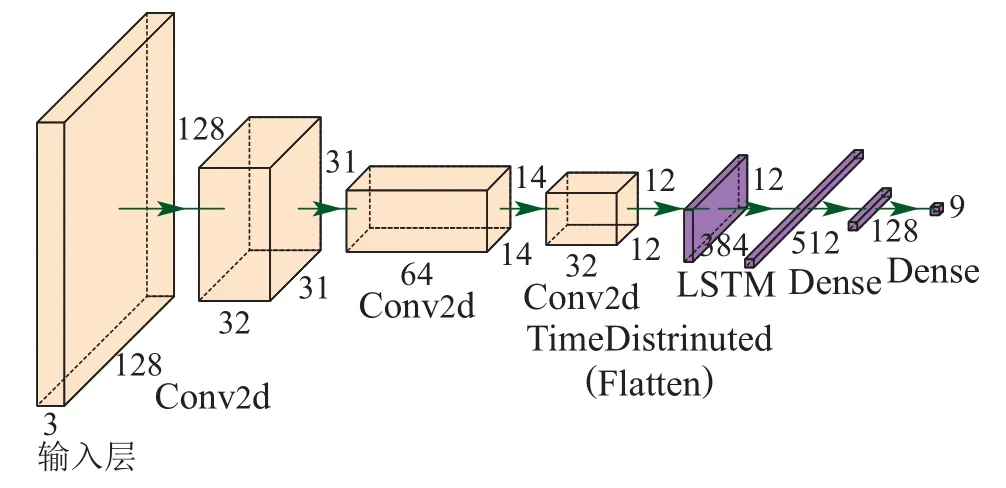
图1 时序网络结构Fig.1 Time-series network structure

在该网络结构中,通过前面3层Conv2卷积层,对输入状态进行局部空间特征提取,增强网络对静态环境特征的学习;然后,通过Flatten层,在不影响batch大小的同时将状态特征映射为平坦化向量,并通过在外层增加TimeDistributed进行维度扩张,以满足LSTM层的维度需求;接着,通过LSTM层增加网络对时空综合特征的感知,以及对时序特征的捕获;最后通过Dense层输出最终结果.所以,该网络不仅能够很好地捕获状态的局部空间特征,还能够对具有长期依赖关系的数据进行时序预测,获取状态间的时序相关性,提升网络对数据利用效率,并且网络结构相对简单,能够满足无人驾驶实时处理的要求.

4 实验结果与分析

4.1 收敛速度对比

为了验证本文MDTQN算法中的时序网络结构以及多步积累奖励方法中的n值和β值对算法收敛速度和数据利用效率的影响,实验使用了如图2所示的无人驾驶仿真环境.该环境模拟了现实赛车场景,其主要由一条弯曲环形赛道和无人驾驶车辆组成.仿真环境中的每一辆无人车都要求从指定位置出发,围绕车道进行行驶,直至达到最大运行次数或是超出车道.该仿真环境的输入状态信息是对车辆所在位置的鸟瞰图进行灰度化、图像缩放等预处理后,得到的图像信息,最终的效果见图2右下角所示;其奖励值由车辆在车道中的位置决定,其大小等于车辆中心位置到车道中心的距离的负值;智能体输出的车辆控制动作为直行、左转、右转3个值,其网络训练的超参数见表1所示.

图2 无人驾驶仿真环境示意图Fig.2 Diagram of unmanned driving simulation environment

表1 网络训练超参数Table 1 Network training hyperparameters

首先,将原始DQN算法和DDQN算法与使用时序网络的DQN算法(DTQN)和DDQN算法(DDTQN),在相同环境下进行对比实验,最终的实验结果如图3所示.从图中可知,DDTQN算法在该环境下训练60轮后达到收敛,DTQN算法在75轮时收敛,DDQN算法在82轮时收敛,DQN算法在96轮时收敛.实验结果说明,增加时序网络后DQN算法和DDQN算法的收敛速度,在原始DQN算法和DDQN算法的基础上分别提升了21.9%和26.8%,表明了时序网络结构在相同环境中,相较于传统CNN网络能够很好的处理状态间的长期依赖关系,并有利于状态间的时序特征地提取,从而提升智能体对时域数据的利用率,以及加快了网络的收敛速度.

图3 时序网络收敛速度对比Fig.3 Time-series network convergence rate contrast

为了验证多步积累奖励方法中不同n值和β值对智能体收敛速度的影响,使用与上一实验相同的仿真环境和超参数,将三次仿真训练的平均收敛轮次作为最终结果,具体如表2所示.由表2可知,当n=1时,不同β值的算法收敛轮次相同,说明此时奖励回报函数仅与当前奖励有关,β值仅充当当前奖励值的常值系数,对智能体的训练没有影响.因此,在不同β值下的训练速度一样.本文设计的多步法在2 ≤n≤7时,算法达到收敛需要的训练轮次的均值都小于原始DDQN算法(n=1),这说明多步积累奖励方法能够有效的提高智能体对数据的利用效率,加快算法的收敛速度.但是,当n≥8时,其收敛速度比原始DDQN算法慢,这是由于无人驾驶环境较为复杂,智能体为避免产生碰撞或是其他灾难性动作而偏离车道的中心位置,从而降低了智能体的奖励,减慢了收敛速度.另外,当β值较小时,智能体平均收敛速度较慢,这是因为智能体忽略了当前即时奖励的重要性,而更多的将未来奖励作为判断当前动作的标准,导致智能体对当前动作认识不足;当β=0.6时,其平均收敛速度达到最佳.根据以上分析,本文设计的多步积累奖励方法(n=5,β=0.6)在无人驾驶环境中,能够有效的提升智能体对数据的利用效率,加快网络的收敛速度.

表2 不同n值、β值收敛轮次Table 2 Convergence rounds corresponding to different n and β values

为了进一步验证本文MDTQN算法中多步积累奖励方法对数据利用效率的优越性,将n步Q学习算法(n=5)、n步Sarsa算法(n=5)与MDTQN算法(n=5,β=0.6)在相同的环境下进行仿真验证,每次训练达到收敛的轮次结果如图4所示.由图4可知,n步Q学习算法和n步Sarsa算法达到收敛的轮次相似,其收敛轮次均为55轮左右,这是由于二者的算法结构相似,仅在价值函数的更新上存在差异.本文设计的多步积累奖励方法在仿真实验中收敛轮次为40轮左右,其收敛轮次明显小于其他两种多步即时奖励算法.这说明本文设计的多步积累奖励方法能够有效地加快智能体的收敛速度,增强智能体对数据的利用效率,以及证明了突出当前奖励值和对多步积累奖励进行均值化处理,有利于提高智能体对数据的处理.

图4 多步法收敛速度对比Fig.4 Convergence speed comparison for different multistep methods

为了进一步验证本文MDTQN(n=5,β=0.6)算法的性能,将在Random Walk任务中RMS error最小的3 组参数(λ=0.9,α=0.2;λ=0.8,α=0.3;λ=0.4,α=0.7)下的TD-lambda算法,与本文算法在相同环境下进行训练,最终的得分曲线如图5所示.从图中曲线可以看出,由于TD-lambda算法中加入了资格迹(eligibility)方法,使TD-lambda算法不用存储中间n步的奖励和状态序列,并且智能体能够无需等待episode 结束再进行价值函数的回报估计,从而使得TDlambda算法能够在训练早期更快的适应训练并表现更好.但是,TD-lambda算法对初始采样状态值函数的估计不准确,误差虽被衰减但会被累计,所以本文算法相较于TD-lambda算法能够更快的达到收敛,以及在训练的后期表现出更好的稳定性.

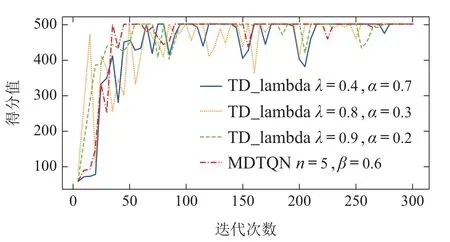
图5 MDTQN与TD-lambda性能对比Fig.5 Performance comparison between MDTQN and TD-lambda

4.2 与现有算法的性能对比分析

为了进一步验证MDTQN算法在无人驾驶中的控制效果和泛化能力,本节实验采用了Carla无人驾驶仿真模拟器[20]作为实验平台,并选用其中的Town01,Town02,Town03小镇场景作为实验地图,具体如图6所示.仿真环境以及车辆的参数设置参考文献[21],状态、奖励和动作的设置做了如下调整.

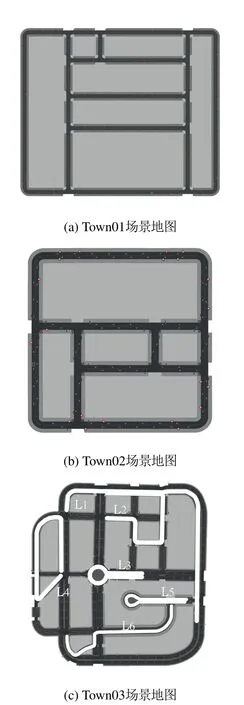
图6 不同场景下的仿真地图Fig.6 Simulation maps in different scenarios

首先,仿真环境中的状态信息地获取是通过在无人汽车上放置摄像头拍摄得到的原始图像,然后通过Carla模拟器中的工具包进行语义分割和特征提取,接着进行图像的灰度处理和压缩处理,最后将处理后的3帧图像合并作为最终输入状态.无人汽车采用离散动作空间,并且使用二维向量进行表征,即a=(acceleration,steer).其中,acceleration 表征汽车的加速度大小;steer表征转向的角度大小.在实验中,将加速度设置为-1.0,0.0,1.7,转向值设置为-0.3,0.0,0.3,将不同的加速度和转向值组合得到9种动作,从而得到无人驾驶的动作空间.实验奖励值的设定是根据汽车状态的安全性和自身速度进行定义,具体函数如下:

其中:λ是碰撞的影响因子;collision是碰撞的标志位,取值为1或-1;µ是车道超出的影响因子;S是车辆超出车道的面积;v是汽车的当前速度;vmax是汽车的最大速度.

为了验证本文提出的MDTQN算法在复杂环境中的收敛速度和控制性能,实验将MDTQN算法(n=5,β=0.6)与两种基于价值迭代的算法(DDQN,DQN),在图6(a)所示的Town01场景相同条件下进行训练,其训练网络的超参数设置如表1所示,其中的训练回合数更改为3000,每回合最大运行的次数更改为1000次,训练的得分曲线如图7所示.从图中可以看出,由于对训练车辆进行了车道超出限制,以及地图中存在急弯和障碍物等复杂条件的约束,导致DDQN和DQN算法不能达到MDTQN的最终收敛状态,其最终得分稳定在600分以下.本文提出的MDTQN算法在训练的前期与DQN和DDQN算法相似,都不能够较好的处理复杂的约束条件,但由于设计了多步积累奖励方法,加强了智能体对时域数据的利用效率,进而加快了智能体的训练速度,以及时序网络结构的设计能够更好地处理弯道状态的时序特征.因此,本文MDTQN算法在经过1250轮左右的训练,逐渐学会了在复杂环境中进行驾驶控制,最终得分收敛于800分左右.从图7中也能够看出,在训练的前半段,本文MDTQN算法训练的速度明显快于另外两种.所以,这表明本文提出的MDTQN算法相较于其他两种算法的学习能力更强,数据利用率更高,并且对于复杂环境有更好的控制性能.

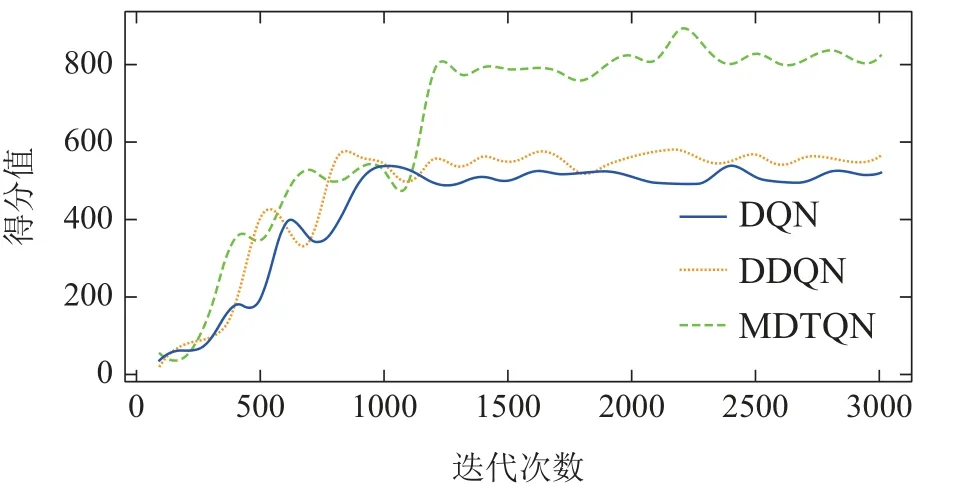
图7 不同算法训练迭代的奖励Fig.7 Rewards for training iterations of different algorithms

为了进一步验证本文MDTQN算法的控制性能,选如图6(b)所示的Town02作为实验仿真地图,超参数的设置与上一实验相同.表3给出了文献[5]中的模仿学习(imitate learning,IL)算法、文献[21]中的双延迟深度确定性策略(TD3)算法以及文献[17]中的DDQN算法与MDTQN(n=5,β=0.6)算法,在典型Town02场景中进行10次测试得到的各项得分指标数据.从表3中可以看出,由于IL通过专家数据进行训练,在与训练场景相似的环境中能够获得很好的表现,因此,IL算法在各项指标上明显优于其他算法.而本文提出的MDTQN算法的得分稍低于IL而高于另外两种,在DDQN算法的基础上增加了36.1%,比TD3算法高了24.6%.由于TD3算法在深度确定性策略梯度(DDPG)网络上做了3个重要的优化,并且在测试中使用了连续的动作空间,因此,其得分比DDQN 算法高了15.3%.

表3 Town02场景各算法得分Table 3 Score of each algorithm in Town02 scene

为了验证本文MDTQN算法在不同环境下的泛化能力和控制能力,选取了Town03场景中6条不同复杂程度的线路进行仿真实验,具体路线信息如图6(c)所示.4种算法均是在Town01场景下进行模型训练,然后针对Town03中不同线路进行10次测试,其平均完成情况如表4所示.从表4中可以看出,在与训练环境相似的线路L1,L2中,4种算法都能够很好的完成行驶任务,其中MDTQN和IL算法都能100%完成L1,L2道路的行驶任务.对于路况较为复杂的L4和L6线路,IL算法和MDTQN算法完成情况优于其他两种算法.在L6线路中,由于存在大量连续弯道,而Town01训练场景中没有这样的状态,所以导致IL算法不能达到MDTQN算法的完成水平.对于路况信息最复杂的L3,L5线路,只有MDTQN算法完成率在一半以上,其他算法的完成率均低于50%.这说明IL算法仅能够在已训练过的场景中取得好成绩,但是对于没训练过的情景将不能够较好的完成控制;而本文MDTQN算法不仅能够在熟悉的场景(L1,L2,L4)中取得与IL算法相近的完成率,对陌生的线路L3,L5,L6也能够较好的完成.这说明本文算法在处理陌生环境和突发情况时,能够表现出了良好的控制能力和泛化能力.

表4 Town03场景平均完成度Table 4 Average completion of Town03 scene

5 总结

本文针对当前无人驾驶强化学习控制决策算法存在无法有效利用时序数据,以及收敛速度慢等问题,提出了一种基于多步积累奖励的双重时序Q网络算法.该算法使用多步积累奖励方法,代替原始DDQN算法中仅使用当前即时奖励的方式,以及对多步积累奖励做了均值化处理,并突出当前即时奖励的重要性;另外,该算法设计了一种将CNN和LSTM相融合的时序网络结构,在捕获输入状态的局部空间特征的同时,增强了网络对状态间时序相关特征的捕获能力,提升了网络对数据利用效率.实验结果表明本文算法能够显著地提高强化学习对时序数据的利用效率,以及加快智能体的收敛速度,并具备良好的泛化能力.