具有未知负载扰动的水井钻机电液伺服系统无模型自适应控制
姚文龙亓冠华 池荣虎 邵 巍
(1.青岛科技大学自动化与电子工程学院,山东青岛 266100;2.北京理工大学宇航学院,北京 100081)
1 引言
本文针对水井钻机电液伺服系统存在的参数不确定以及未知负载扰动突变等问题,提出了基于径向基神经网络扰动观测器的无模型自适应控制方法,解决系统控制精度低、鲁棒性差的问题.电液伺服系统是集机械、电气和液压于一体的耦合系统,具有响应速度快、负载能力强、控制精度高等特点.现已广泛应用于水文勘探[1]、船舶运输[2]、航空航天[3]等领域.但在水井钻探实际应用中,电液伺服系统不仅要考虑由液压缸摩擦特性、泄露特性、伺服阀滞后特性、加载变化、模型误差等造成的影响,还要考虑由于井底岩层未知以及工作进程中大量泥沙喷射所造成的未知扰动的干扰.因此,利用先进的控制方法,提高电液伺服系统的控制精度以及未知扰动下的跟踪性能,具有重要的工程应用价值[4].
目前,针对电液伺服系统中存在的未建模动态以及负载扰动突变造成的非线性问题,国内外学者做了大量研究,并取得了很多有意义的成果.文献[5-7]对电液伺服系统在实际工程中应用广泛的PID控制进行了进一步扩展,像模糊PID控制、基于分数阶的模糊PID控制等;文献[8-9]为抑制电液伺服非线性系统的参数摄动,分别设计了扩展积分控制器和自适应鲁棒控制器,但其算法复杂,参数收敛速度慢;文献[10]针对系统参数不确定的问题,采用Volterra序列进行建模,将滑模自适应控制方法应用到了系统中,但基于负载扰动变化,需要精密的测量工具才能满足稳态误差的要求;文献[11-13]应用模糊滑模控制算法针对难以建模的电液控制系统进行分析,研究了模糊控制与滑模变结构控制的几种结合方法,解决了常规滑模抖振大和控制力频繁切换的缺点;文献[14]提出了基于微分器的backstepping控制方法,采用二阶微分器估计不确定参数并逼近虚拟函数的导数,不需要参数辨识与模型逼近;文献[15]利用backstepping控制方法对电液伺服系统进行设计,通过设计扩张状态观测器来解决系统中存在的非线性不确定参数问题.
事实上,上述基于电液伺服系统的控制方法都对系统模型精确程度依赖性较强,且对于系统中存在的非线性不确定参数都采用了不同的方法进行控制.对于本身为高度非线性的液压系统,尤其考虑是在水井钻机电液伺服系统实际工况中所面对的井底岩层未知,系统运行过程中有大量泥沙干扰的情况,这都增加了系统精确建模的难度.同时,它们对非线性系统的分析都进行了线性化的过程,把线性系统的控制方法推广到了非线性系统,然而,大部分方法需要依赖于被控系统的精确线性化模型,一旦所依赖的精确线性化模型发生变化,控制器将不能保证跟踪误差的单调收敛性;另外,很多控制算法较为复杂,系统参数需要不断进行调整,难以在实际工业情况下实现.因此,设计一种所需系统模型信息少,抗干扰能力强且易于工程实现的控制器具有重要的工程意义.
无模型自适应控制(model free adaptive control,MFAC)[16]是由侯忠生教授提出的一种基于数据驱动的新型控制方法.数据驱动控制是指控制器设计仅利用受控系统的在线或离线I/O数据以及经过数据处理而得到的知识来设计控制器,且不显含受控过程的数学模型信息.针对难以建立系统精确模型的非线性系统,采用基于紧格式的动态线性化方法[17],与上文所提及的控制器所用的线性化[14-15]方法不同的是,该方法得到的线性形式是对原非线性系统的完全等价,含有较少的参数,且这些参数可以利用系统的I/O数据进行估计.由于该方法中没有用到被控系统的任何模型信息,对于难以建立精确模型的水井钻机液压系统具有很好的工程实践意义.
需要指出的是,已有的MFAC算法虽然能够保证系统存在外部扰动时跟踪误差有界,却不能保证系统所受外部干扰过大时控制精度的准确性.在动态线性化的过程中,系统的不确定性可以由所获得线性数据模型的伪偏导数来估计,但是,当被控系统外部负载扰动所造成的不确定性和非线性太强,则伪偏导数的动态特性会难以有效估计[18].
考虑在实际被控系统中广泛存在的干扰和不确定性,利用扰动观测器对系统扰动进行在线估计是处理未知环境扰动的有效方法.文献[19-20]提出了一种非线性扰动观测器用于外部环境恶劣的船舶轨迹跟踪控制中;文献[21]将模糊自适应观测器与反步控制相结合用于跟踪非对称缸轧机液压伺服位置系统;文献[22]将扩张状态观测器用于具有输入饱和的电液伺服系统中.但以上观测器的设计都需要系统模型参数已知,对于系统模型参数时变或未知的电液伺服非线性系统并不友好.
文献[23]提出了一种基于改进的无模型自适应控制算法,将径向基(radial basis function,RBF)神经网络与无模型自适应控制方法相结合,在不需要系统模型参数的基础上补偿系统的非线性和不确定性.RBF神经网络[24]相较于传统的控制方法具有自学习能力,不需要许多的系统模型信息和参数信息,并且多层神经网络的隐含神经元采用激活函数,它的非线性映射功能可以逼近任意的非线性函数.
基于以上分析,本文提出了一种基于径向基神经网络扰动观测器的无模型自适应控制方法来解决水井钻机电液伺服系统中的参数不确定和外负载扰动问题.所提出的基于RBF神经网络扰动观测器的无模型自适应控制方法本质上是一种数据驱动的方法,首先,根据参考文献[21]所提出的动态线性化方法,将非线性的被控系统线性化为含有输入输出以及非线性项增量的形式;接着,设计一种RBF神经网络扰动观测器,对含有未知负载扰动的非线性项进行估计;最后,通过设计含有未知负载扰动估计值的目标函数,提出了估计准则函数与伪偏导数估计律.理论分析与仿真结果证明了所提方法的有效性.该方法针对外界扰动未知,精确模型难以建立的水井钻机电液伺服系统有很好的工程实践意义.
2 电液伺服系统建模
水井钻机电液伺服系统通过伺服阀实现液压油缸活塞位移的控制,阀控非对称液压缸动力机构示意图如图1所示.在阀控非对称液压缸系统中,由于液压缸两腔面积不相等,使得液压缸在左右两个方向运动时,比例增益不相等,故在建立动力机构基本方程时,需要分别考虑.

图1 水井钻机电液伺服系统原理图Fig.1 The principle diagram of water well drilling rig electro-hydraulic servo system
液压油流量与伺服阀阀芯位移之间关系[25]描述为

式中:Q1,Q2分别为液压油缸进油口与回油口流量;w为伺服阀面积梯度;xv为伺服阀阀口开度大小;ρ为液压油密度;P1,P2分别为进油腔与回油腔的压力;Ps为油泵压力;PT为回油压力;Cξ为伺服阀流量系数.
液压油缸流量连续方程[26]为

式中:x1为液压油缸活塞杆位移量;Ct为液压缸外泄露系数;Cip为液压缸内泄露系数;V10,V20为液压缸有杆腔与无杆腔的初始容积;βe为液压油等效体积弹性模量;A1为液压油缸有杆腔活塞作用面积;A2为液压油缸无杆腔活塞作用面积.
系统的力平衡方程[27]为

式中:Mt为折算到柱塞上的总负载质量;K为负载弹性刚度系数;Bc为活塞的粘性阻尼系数;F为外负载力.
由于伺服阀的频带宽度远大于液压系统的固有频率,因此伺服阀输入电压与阀芯位移的关系可等效为比例环节[28]

其中:kv为比例增益系数;u为伺服阀输入电压;且kv>0.
令x1=x,x2=,x3=,其中:x2为液压缸活塞杆速度;x3为液压缸活塞杆加速度.联立上式可得水井钻机电液伺服系统的状态空间方程[29]
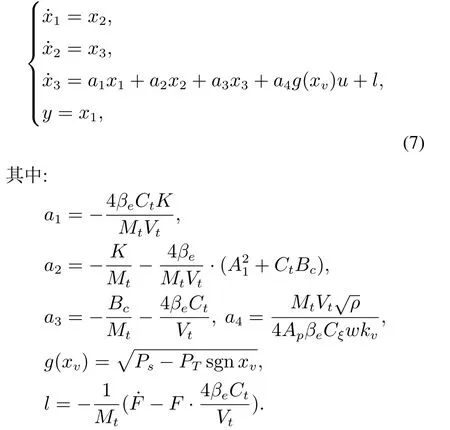
在系统运行过程中,负载质量Mt、液压弹性模量βe、伺服阀面积梯度w、粘性摩擦系数Bc等都会随着工作状态、温度以及设备磨损的变化而变化.系统方程中的参数均为系统额定负载时的标准值,实际系统中a1,a2,a3,a4都是未知时变的,并将系统的外负载扰动、未建模动态、可分离参数都归到l中.
液压油缸活塞的运动快慢由进入液压油缸的流量大小决定,故调节阀芯开度大小,就可以改变进入油缸的液压油的流量,进而改变液压油缸活塞的运动速度与负载位移.当控制输入电压信号为零时,阀芯位移为零,此时阀芯处于中位,液压油缸流量为零,水井钻机电液伺服系统停止动作.因此,调节系统的控制输入电压信号就可以改变水井钻机电液伺服系统的推进速度.
3 控制器设计
取采样周期为h,采用前向差分法,将上式的状态空间方程离散化为
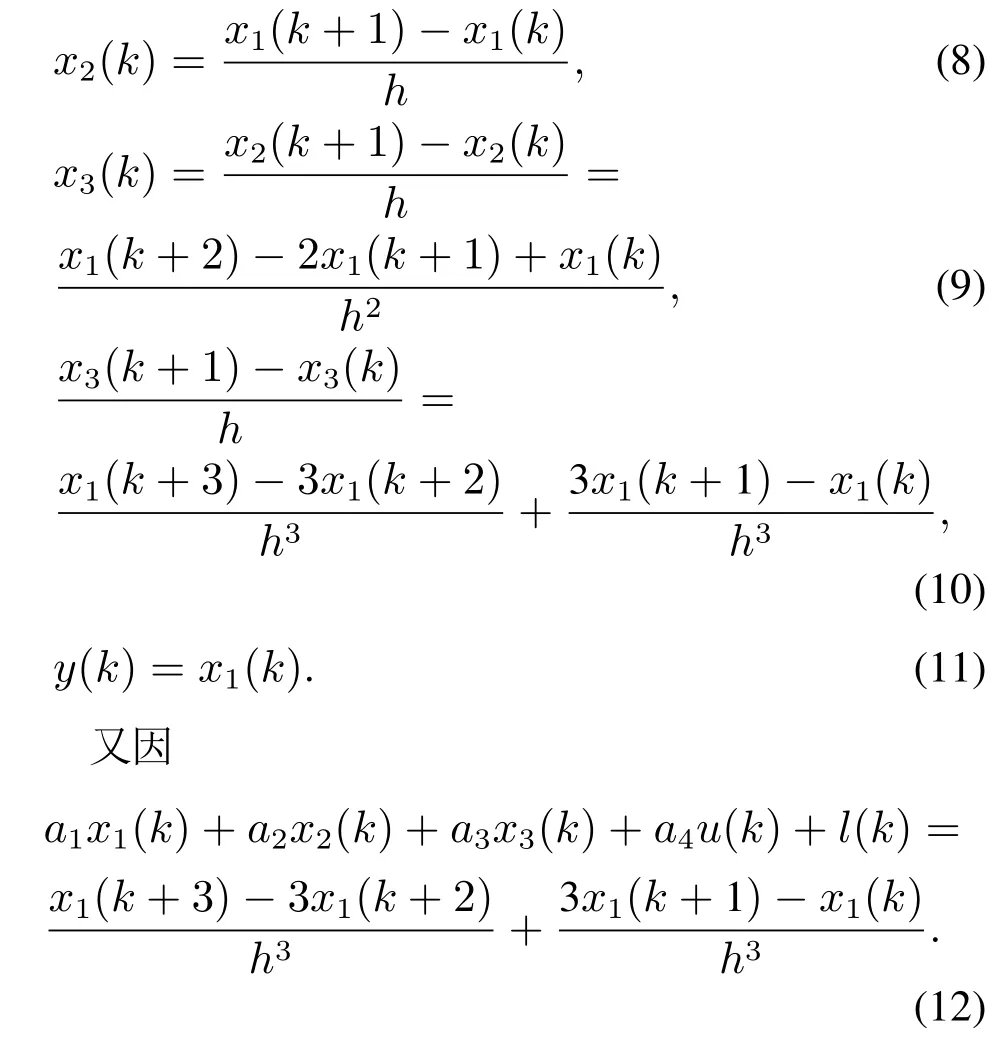
整理得离散时间非线性系统

将离散时间非线性系统整理为如下形式:

式中:u(k)∈R,y(k)∈R,分别为k时刻系统的输入与输出,k ∈{0,1,···,T},T是正整数;f(·)是系统未知的非线性函数;l(k)包含k时刻系统未知负载扰动、未建模动态、可分离参数等,|l(k)| 水井钻机电液伺服系统是一个连续运动的系统,其动态过程满足一定的光滑性;并且当输入的控制电压在伺服阀运行的允许范围之内,输入电压的有界变化引起的液压油缸活塞杆位移也是有界的;另外,非线性扰动量为有界的,因此水井钻机电液伺服系统满足无模型自适应控制方法中要求的非线性系统在进行紧格式动态线性化过程中所要求的假设条件,即: 假设1除有限时刻外,f(·)关于控制输入信号u(k)、扰动信号l(k)的偏导数存在连续且有界. 假设2除有限时刻外,系统满足广义Lipschitz条件,即对任意时刻k1/=k2,有 式中:p1>0,p2>0为常数. 定理1对满足假设1和假设2的非线性系统(14),若满足假设1和假设2,则当|Δu(k)|/=0时,一定存在时变参数θ(k),使得 对于每一个固定时刻k,考虑含有变量η∗(k)的数据方程,故当|Δu(k)/=0|时,一定存在唯一解η∗(k),使得θ(k)= 故可得如下数据模型: 证毕. 注1与无模型自适应控制算法中紧格式动态线性化的方法不同,新型的动态线性化数据模型引入了未知扰动项l(k),通过未知扰动项l(k),数据模型可以对一般的负载扰动进行描述,并且式(16)中的θ(k)的控制增益的复杂度将大大降低,可以更容易估计. 在水井钻机电液伺服系统中,由于液压油缸的摩擦特性,伺服阀的死区特性以及未知负载扰动的不确定性在进行数学建模的过程中往往被忽略,这些因素会使系统的动态性能变差,控制精度降低.采用无模型自适应控制器解决了电液伺服系统难以精确建模的问题,但在工况恶劣的水井钻机电液伺服系统中,负载扰动的影响是难以忽略的.因此采用RBFNN扰动观测器对水井钻机电液伺服系统中存在的非线性扰动进行估计,并将估计量作为无模型自适应控制器的非线性项进行处理,以提高系统的鲁棒性和稳定性. 针对式(16)中的未知参数Δl(k)采用RBF神经网络扰动观测器[24]对未知参数进行估计.该系统的输入向量为 是为隐含层第j个神经元高斯基函数中心点的坐标向量,i=1,2,···,n为迭代次数;η为学习速率,α为动量因子. 针对水井钻机电液伺服系统负载扰动突变造成的跟踪性能差以及控制精度低的问题,设计了基于RBF神经网络的无模型自适应控制(model-free adaptive controler based on RBF neural network,MFAC-RBFNN)方案.利用输入电压与输出活塞杆位移的数据,设计无模型自适应控制器,同时结合RBFNN扰动观测器作为反馈装置,构成基于RBFNN扰动观测器的水井钻机电液伺服系统无模型自适应控制方案,控制框图如图2所示. 图2 电液伺服系统MFAC-RBFNN扰动观测器控制框图Fig.2 The control block diagram of electro-hydraulic servo system MFAC-RBFNN disturbance observer 构造输入准则函数: 式中:λ为权重因子,y∗(k+1)为k+1时刻的期望输出信号. 式中:λ>0,µ>0,η ∈(0,1]为步长因子;ρ1,ρ2为迭代步长. 由于伪偏导数θ(k)未知,考虑如下伪偏导数估计准则函数J[(k)]的最优解: 对该准则函数关于θ(k)求极值,可得伪偏导数估计律 图2中y∗(k),y(k),u(k),e(k),l(k),分别为电液伺服系统期望位置跟踪信号、系统输出信号、系统输入系信号、跟踪误差信号、外负载扰动信号、非线性项估计值. 注2基于扰动观测器的无模型自适应控制算法,未知的控制增益θ(k)与未知的非线性负载扰动Δl(k)分别用不同的算法进行估计,即式(23)和式(35).并且Δl(k)的估计值被用于θ(k)的更新律中以起到补偿作用. 由于RBF神经网络能够以任意精度逼近任意光滑的非线性函数,选择适当的网络结构和网络参数,便可实现对Δl(k)任意精度的逼近.于是存在一个很小的正数ϱ,使得估计误差始终小于ϱ[24],即 为了严格讨论,对水井钻机电液伺服系统给出如下假设与定理. 假设3对于任意时刻k,系统伪偏导数θ(k)的符号保持不变. 定理2对于水井钻机电液伺服系统式(14),在假设1-3均成立的条件下,在负载扰动满足|l(k)| 证 定理2的证明分为3大部分.分别为伪偏导数估计值θ(k)、跟踪误差e(k)以及系统输入输出的有界收敛性. 当|Δu(k)|≤ε,由重置算式(36),(k)显然是有界的. 定义: 定义跟踪误差为 注3为估计负载扰动Δl(k)引入了RBF神经网络扰动观测器,根据定理2仍能保证伪偏导数(k)的估计值是有界的,同时式(42)也保证(k)的估计值是有下界的[30]. 为验证本文控制方案的有效性,在MATLAB/Simulink仿真环境下建立了阀控非对称缸的液压伺服系统,仿真参数采用山东省发改委重点项目工程样机-全液压顶驱回转式水井钻机数据,如表1所示.针对水井钻机电液伺服系统,本文将基于非线性扰动观测器的自适应控制[19,29](APC-NDO)、传统MFAC控制与所提的MFAC-RBFNN控制策略进行仿真比较,验证了本文所提方法的合理性与有效性. 表1 水井钻机电液伺服系统参数Table 1 The parameter of electric hydraulic servo system of water well drilling rig MFAC-RBFNN的参数选择为 其中:RBF神经网络在仿真过程中为在线训练,训练样本为2000个,RBF在初始状态设置权值、高斯函数参数wj,rj为[-1,1]的随机数,高斯函数宽度bj=1.在整个训练过程中误差收敛于[-0.015,0.015]. 图3与图4分别为在MFAC与MFAC-RBENN控制下系统的输出位移曲线、位移跟踪误差曲线.横轴为系统运行时间,纵轴为系统控制量.仿真中采用复杂随机信号作为扰动信号,由图3可知,传统MFAC算法与MFAC-RBFNN算法均可实现稳定控制,MFACRBFNN控制算法相比MFAC算法对未知负载扰动进行了估计与补偿,能够抑制负载扰动带来的振荡,使其鲁棒性与控制精度大大提高.从图4可知,本文所提方法能够在0.19 s左右误差达到最小值,实现RBF神经网络对未知负载扰动信号的跟踪,使得本文方法相较于传统MFAC控制方法,系统输出误差更小,控制效果得到了改善. 图3 位移跟踪曲线Fig.3 The displacement tracking curves 图4 位移跟踪误差曲线Fig.4 The displacement tracking error curves 图5与图6分别为正弦信号输入下水井钻机电液伺服系统的位移跟踪曲线与跟踪误差曲线.横轴为系统运行时间,纵轴为系统输出量.将本文所提方法与APC-NDO控制方法相比较,本文所提方法输出曲线的振荡更小,误差跟踪效果更优异.APC-NDO控制方法通过对未知参数进行估计,进而设计非线性扰动观测器,与本文所提方法相比控制器设计更复杂,并且考虑实际工程的复杂性,本文所提方法能够有效克服系统非线性的影响,大大提高系统性能. 图5 位移跟踪曲线Fig.5 The displacement tracking curves 图6 位移跟踪误差曲线Fig.6 The displacement tracking error curves 本文针对具有参数不确定以及负载扰动突变的水井钻机电液伺服系统,利用基于径向基神经网络扰动观测器的无模型自适应控制方案,以改进系统的跟踪性能和控制精度.该方案利用改进的动态线性化方法,将被控系统线性化为与I/O相关的增量形式,并将未知负载扰动合并到一个非线性项中;然后分别利用时变参数估计律和RBF神经网络扰动观测器估计未知时变参数和非线性扰动项;进而设计了水井钻机电液伺服系统的控制更新律.仿真结果验证了该控制方案应用于水井钻机电液伺服系统的有效性,并克服了系统设计与分析依赖精确模型建模的局限,其控制精度高、动态响应快、鲁棒性强,补偿了未知负载扰动带来的影响,有效提高了系统的抗干扰能力.在本文基础上,将该控制方法应用于全液压顶驱回转式水井钻机样机进行工程测试,将是后续工作的重点.3.1 动态线性化


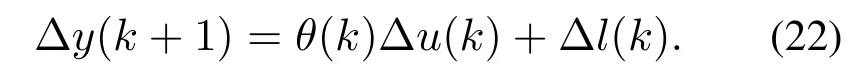
3.2 RBF神经网络扰动观测器的设计



3.3 基于RBF神经网络的无模型自适应控制器设计




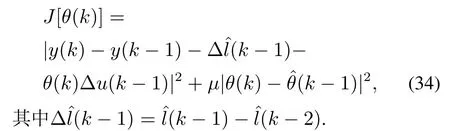

4 收敛性分析



4.2 I/O的有界性
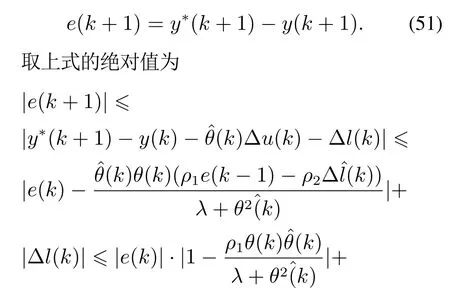



5 仿真结果分析




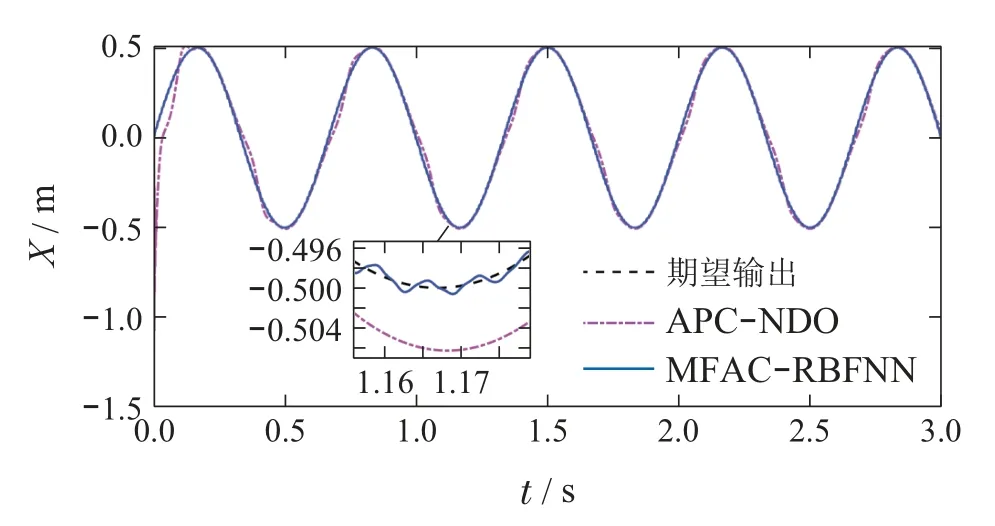
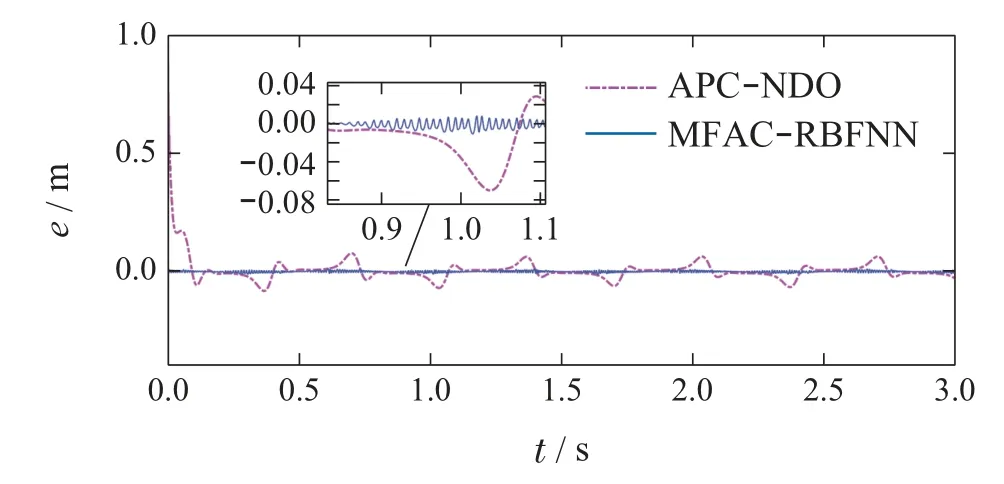
6 结论

