锌电解行车自适应在线轨迹规划方法及应用
唐峰润,阳春华,李勇刚,朱红求,李繁飙,周 灿
(中南大学自动化学院,湖南长沙 410083)
1 引言
锌是我国重要的有色金属原材料,其电解是锌冶炼的关键工序.行车又称桥式起重机,是锌电解车间用于完成阴阳极板转运任务的重要装备,其运行效率是决定电解产能的关键因素.由于锌电解车间现场环境恶劣,人工驾驶行车劳动强度大、生产效率低.因此,研发锌电解行车精准定位算法和自动控制系统具有非常重要的实际意义.
近年来,国内外研究人员大都基于起重机轨道状态良好,摩擦系数不变的假设,进行了大量定位消摆方法的研究[1-5].而针对锌电解车间轨道状态多变引起的摩擦系数发生变化且无法确定的难题,目前相关研究非常少,研究此类问题极具挑战性.工业起重机系统,其台车的快速精准定位与有效载荷的消摆通常是相互矛盾的,如何同时实现这两方面的控制目标,并且达到较好的控制效果,具有较高的难度.目前,有关学者提出了一些解决方法,可将其分为开环控制系统和闭环控制系统.起重机闭环系统旨在找到一种使系统稳定的反馈控制律,使用系统当前状态的信息来将系统驱动到所需状态.文献[6-7]提出基于反馈线性化的控制方法,简化了系统算法的设计.文献[8-9]提出无源控制的技术,可以很好的解释控制律的物理含义,并且实现形式简单.文献[10-12]提出自适应控制的方法,解决了参数不确定性和外部干扰等问题.文献[13]利用模型预测控制来解决起重机控制的约束问题,获得了较好的效果.近年来,进化算法、模糊控制等智能控制方法在起重机控制领域也有着非常广泛的应用[14-15].闭环控制方法虽然在消摆的基础上保证了台车的运行效率,但由于需要采用多种传感器来实时获取系统的状态信息,往往成本较高且难于现场应用.考虑成本以及工程可实现性,工业现场往往采用更为简便的开环控制方案.轨迹规划作为一种常用的开环控制方法,可以预先计算控制效果的一些核心指标如有效载荷摆角和运输效率等,并对其进行约束从而达到控制目的.文献[16-17]设计了一种基于自适应轨迹跟踪控制方案,通过抑制有效载荷的摆动来准确定位.文献[18]提出了一种基于相平面分析的离线几何轨迹规划方法,通过设计不同类型的加速度轨迹来抑制摆角,并成功解决了台车运动与有效载荷摆动之间的耦合行为.考虑到工业现场存在的障碍物,文献[19]提出了一种能有效避免障碍物的轨迹规划控制方法.文献[20]提出了基于能耗最小的最优控制轨迹规划方法.文献[21]针对工业桥式起重机无法实时跟踪给定轨迹、低速段特性差等问题,提出了基于相平面分析的在线轨迹规划方法,构建定位消摆轨迹,无须离线迭代优化,有效的实现了消摆定位.上述轨迹规划方法虽然有效实现了控制目标,但没有充分考虑台车的运行效率和各种约束,文献[22]纳入最优规划的思想,提出了最短时间轨迹规划方法,并采用拟凸优化的技术进行求解,取得了优越的控制效果.
尽管如此,上述方法在使用伺服电机的实验室环境下小型起重机测试平台进行验证,由于伺服电机的精度高,所以能取得较好的控制效果.但上述环境下只考虑理想的轨道状态,难以反映工业起重机的实际运行状态.而锌电解车间行车系统有着负载大、惯性大的特点,采用大功率的三相异步电动机进行驱动,运行过程中其速度轨迹跟踪效果差且轨道工况变化大,现有方法难以直接适用于锌电解车间.
针对锌电解车间轨道摩擦系数变化且无法确定、状态无法评估的问题,本文提出一种行车自适应在线轨迹规划方法.具体而言,首先,针对行车轨道湿滑程度不一、摩擦系数时变,从而引起轨道状态多变的问题,设计了一种基于滑移率的轨道状态评估方法,确定了摩擦系数随滑移率变化的关系并建立锌电解行车模型.接着,设计5段式分级制动策略,对部分轨迹参数进行离线计算.然后,基于状态评估结果和激光测距仪的实时感知数据,设计自适应更新策略并在线更新轨迹中的相关参数.最后,将本文所设计的系统在某大型国有锌冶炼企业的锌电解车间进行应用,取得了很好的实际效果.
2 系统模型
2.1 通用行车模型
行车的运输任务主要由大车、台车以及起升机构来共同完成,对系统可建立三维模型[1],由于其运动过程处于解耦状态,且摆角由大车、台车以及绳长决定,因此可简化为如图1所示的二维欠驱动行车系统,来完成水平过程中的运输任务,模型的通用形式可表示成以下形式[23]:

图1 二维行车系统示意图Fig.1 Schematic illustration of a 2-D crane system
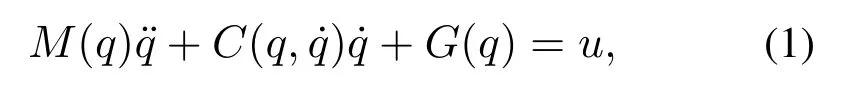
其中:q=[x θ]T∈R2表示系统的状态向量,u ∈R2表示控制输入向量,M(q)∈R2×2,C(q,˙q)∈R2×2,G(q)∈R2,分别表示为系统的惯性矩阵,科里奥利向心矩阵和重力向量,被定义为以下形式:

式中:M和m分别代表台车和有效载荷的质量,x表示台车运行过程的位移,θ表示有效载荷的摆角,l表示吊绳的长度,和分别表示有效载荷的角速度与角加速度,g为重力加速度,µ为轨道摩擦系数,fr=µ,f和fr分别表示台车运行所受的驱动力和摩擦力.
2.2 考虑轨道状态的锌电解行车模型
轨道的摩擦系数µ通常有两种确定方式:实验测定法和考虑材料性质的资料查询确定法.由于锌电解车间轨道摩擦系数会发生变化且难以测量,无法评价轨道状态.针对上述问题,提出一种基于滑移率的轨道状态评估方法并建立锌电解行车模型.
锌电解行车长期在潮湿环境下进行搬运作业,由于轨道摩擦系数µ的减小,导致台车的驱动力矩大于车轮与轨道之间的附着力,当驱动力矩大过于两物体之间的附着力时会发生打滑现象,打滑时车轮的运行速度与车体的运行速度会有所差别.相关学者在飞机、高速列车打滑的研究中[24-25],通常用滑移率来描述打滑现象,如式(4)所示.针对台车打滑问题,本文基于滑移率并充分考虑行车运行过程中可观测的参数,确定轨道状态的评估结果.

其中:k表示台车传动机构的减速比,n表示台车的实际转速,r表示车轮的半径,v1和v分别表示台车运行的理想线速度和实际线速度.行车行驶的过程中由于v无法精准测量,因此利用激光测距仪获取台车实际行驶距离da从而减少σ的误差.

其中σ定义为轨道状态评估结果,通过分析理想和实际行驶距离的关系,对轨道状态进行评估.台车车轮与轨道之间的摩擦系数µ是一个动态变化的量,通过分析打滑机理,摩擦系数与滑移率存在着某种复杂的非线性关系,在钢轨上行驶的高速列车车轮与轨道之间的摩擦系数µ是关于σ的函数[26],表示为
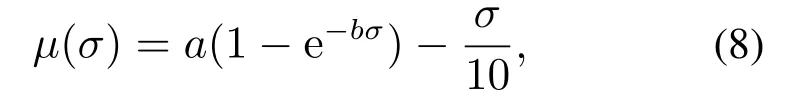
式中a,b是由轨道条件决定的参数变量.
经过大量的实验测试,当车轮与轨道的接触面处于潮湿状态时,a和b取0.275和40;干湿适中状态下取0.32和25;干燥状态下取0.375和15.3种轨道状态下的摩擦系数与滑移率变化趋势如图2所示.
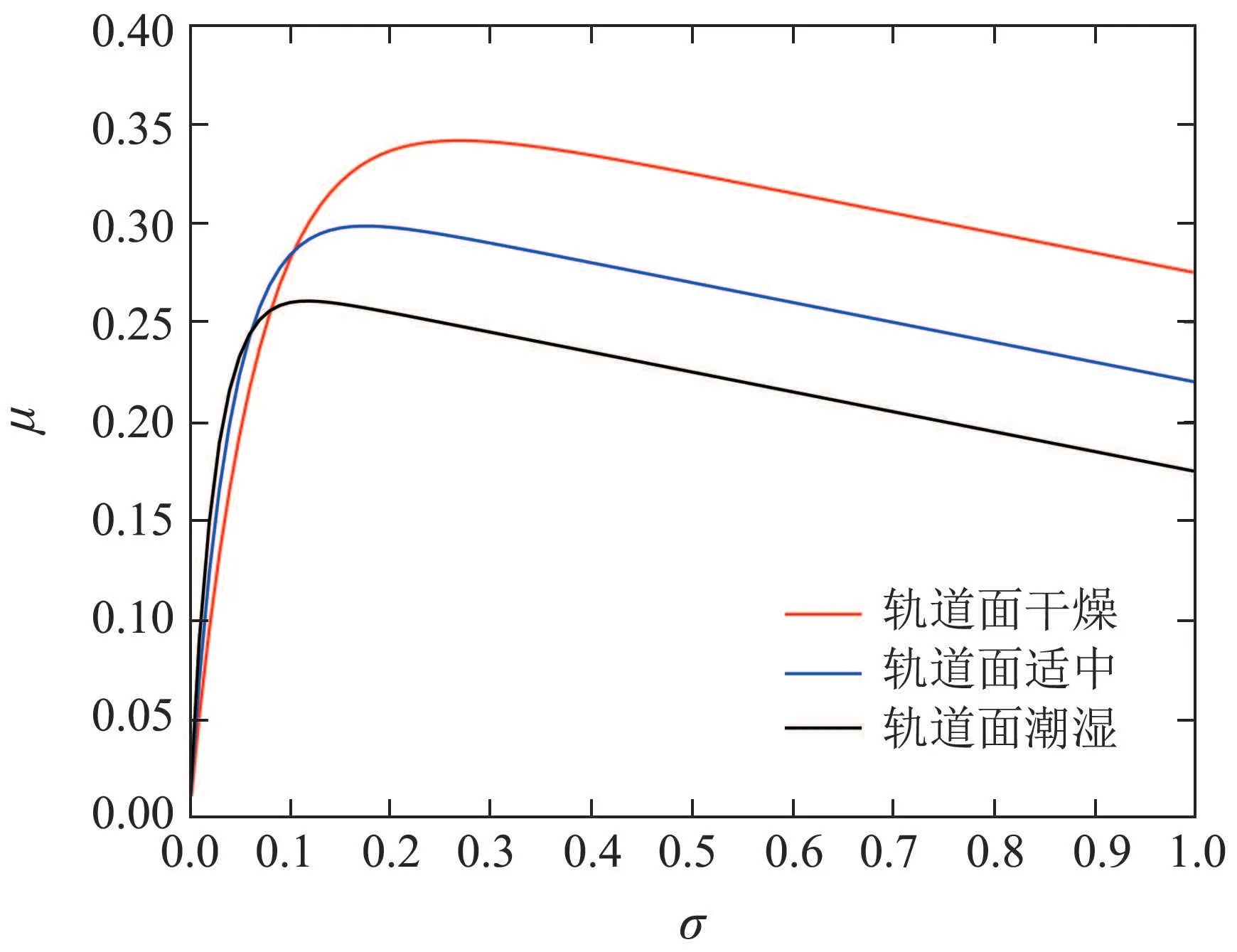
图2 摩擦系数µ与滑移率σ的变化趋势Fig.2 Variation trend of friction coefficientµand slip rate σ
锌电解车间轨道材质为钢铁,查询《实用钢铁材料便查手册》可得滚动摩擦力系数为0.165,考虑锌电解车间轨道磨损、粉尘等影响,最终a取0.2.基于上述3种轨道面的分析并考虑车间内受酸雾等影响,选择情况一的部分参数,b取40.最后联立式(8)和式(3),得

代入式(1)从而建立摩擦系数随滑移率变化下的锌电解行车模型.
3 自适应在线轨迹规划方法
自适应在线轨迹规划方法分为两步,第1步设计5段式分级制动的控制策略,离线计算各阶段的参数;第2步设计自适应更新策略,在线更新轨迹参数并确定行车最佳制动时机,保证运行效率和摆角满足要求.
锌电解行车因环境恶劣、常年作业引起轨道磨损、异步电动机低速段特性较差等原因,造成加减速过程不对称.而标准3段式离线轨迹规划[21],必须保证台车加减速过程完全对称,才能以最大效率达到定位要求.为了确保锌电解行车的定位效率,在3段式轨迹的基础上引入分级制动策略,考虑摆角约束的情况下提出一种自适应在线轨迹规划方法.
台车整个运行过程可由5个阶段进行描述,第1阶段从静止状态以最大加速度运行至最大允许速度,此时进入匀速运行的第2阶段.在传统的离线轨迹规划方法中,第2,3阶段的过渡时机是固定的,无法满足锌电解车间的定位需求.本文通过安装在台车上的激光测距仪来确定切换到第3阶段的最佳制动时机.第4阶段为低速运行阶段,台车从最高速度先降速到给定的允许最低速度,以此速度稳定运行一段时间来保证安全制动.第5阶段低速斜坡减速,保证台车正好精准定位.基于上述分析,针对工业行车的运行特点及所面临的挑战,本文规划的5段式分级制动速度关系见式(9),相应速度曲线如图3所示.

图3 在线速度曲线轨迹规划Fig.3 Online speed curve trajectory planning
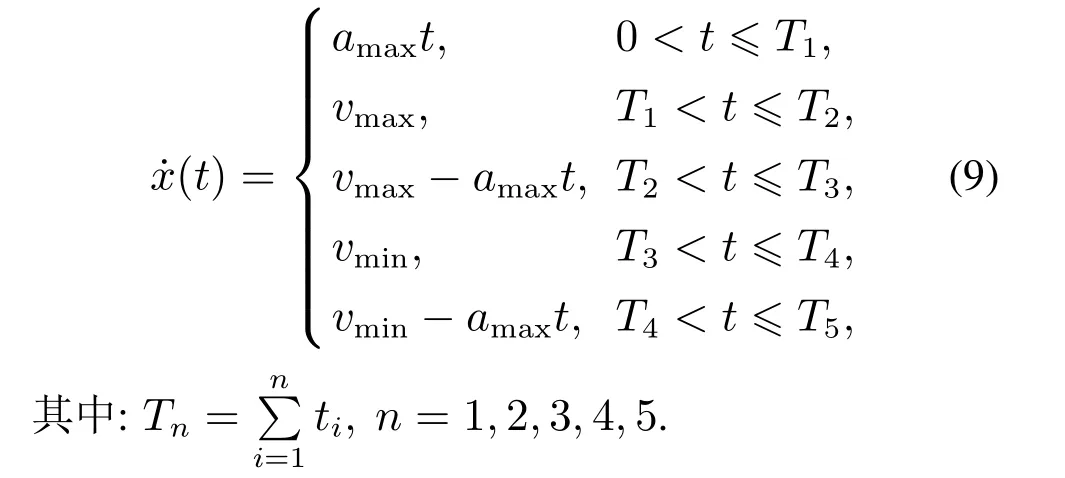
为保证负载摆角在允许范围内,基于锌电解行车模型,采用相平面分析方法对摆角进行约束,确定轨迹中的相关参数.设台车运动过程中恒定加速度为a,对式(1)进行数学推导[18],可得相平面速度曲线方程表示如下:
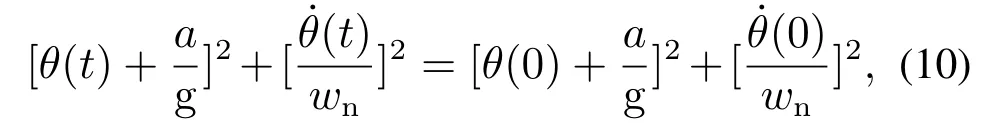
其中:wn=表示有效载荷的自然摆动频率,θ(0)和(0)表示初始摆角和初始角加速度.式(10)可表示为以
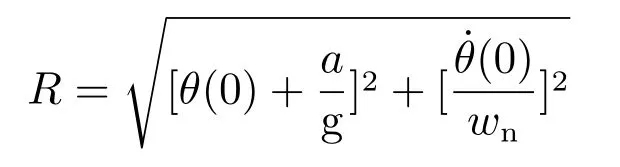
为半径,以(-,0)为圆心的圆.
结合式(10)并对图4进行简单分析,当系统恒定为最大加速度,可以构造出标准的3段式轨迹.a>0时,以(-,0)为圆心,R为半径,负载以恒定角速度wn做顺时针单摆运动,到达A点时摆角最大.a=0时,以(0,0)为圆心保持相对静止.a<0时,O2同理O1,做顺时针单摆运动.
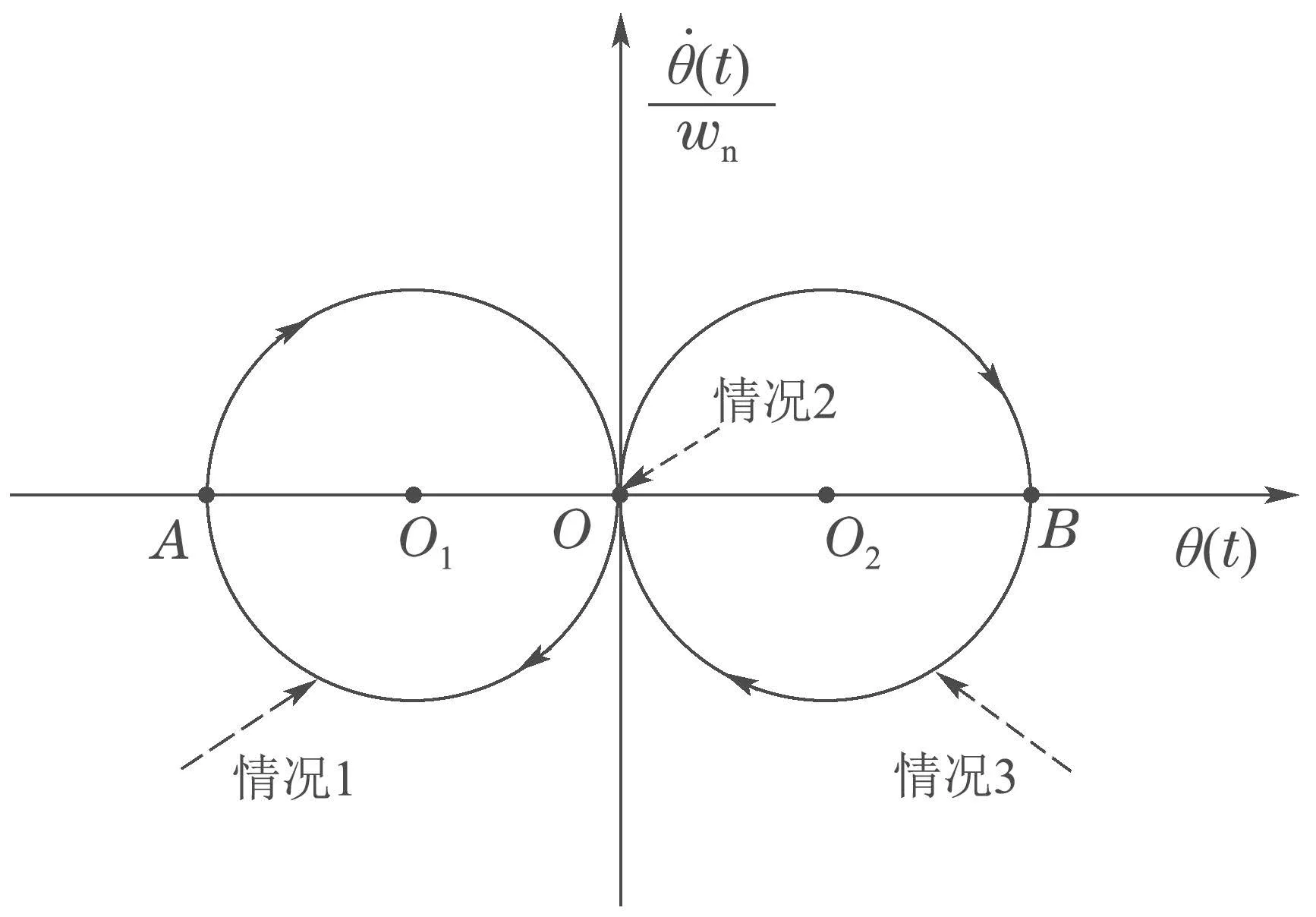
图4 基于相平面分析的轨迹规划Fig.4 Trajectory planning based on phase plane analysis
要获得整个过程的运行轨迹,首先要确定每个阶段的运行时间.第1,2,5阶段的运行时间t1,t3,t5离线计算可得.第2,4阶段的运行时间t2,t4通过自适应更新策略在线更新.具体表示如下:

其中:pd表示目标行驶距离,db表示台车从vmax开始减速时离目标位置的距离,定义为制动距离.理想运行状态下,加减速过程完全对称时运行时间最短,此时有d4→0,则t1=t3+t4+t5,d1=db,联立式(12),式(11)可化简为

实际运行过程中需满足t2≥0,才能保证台车能加速到最大速度并且安全减速制动,此时vmax满足

θml表示台车运行时允许的最大摆角,基于相平面分析的方法可知θmax必须满足摆角在安全范围内的限制条件,表示如下:
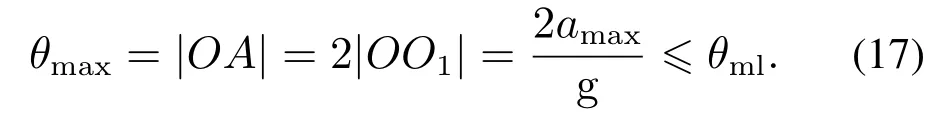
加速度由变频器中设置的加减速时间来决定,其定义为转速从零加速至所定义最大转速所需要的时间.当速度给定的增长速率快于所设定的加速速率,电机转速会遵循此速率;反之,遵循给定;由上述分析可知台车加速度不能超过机械允许的最大上界,表示如下:

其中:ab表示可修改的加速度上界,aml表示台车机械允许的最大加速度,进而可得vmax≤abt1,基于以上分析,vmax必须满足

其中vml表示台车机械结构允许的最大运行速度,为了保证运行效率最佳,需对式(19)取等号.
首先离线计算各阶段参数.第1阶段为加速过程,由图4相平面分析可知,考虑摆角最小的情况下此阶段加速时间为自然振荡周期T,t1=T=,从O点出发沿着O1以角速度wn顺时针旋转一周回到O点,保证了系统加速完成之后摆角仍为0.为了提高生产效率,保证工厂的经济效益,锌电解车间往往要求行车在指定作业周期内完成.若以T作为此阶段的加速时间,其最大速度达不到机械允许的vmax,因此设定系统的加速度为变频器允许的最大加速度,可得第1阶段的加速时间为

第3阶段台车从最大速度vmax以加速度-amax减速到最低安全速度vmin.当vmin过大时台车不能准确定位,过小时导致运行效率低下,因此vmin的选取尤为关键.结合现场实验数据并建立现场速度与制动距离的关系表,从而确定最佳vmin,计算得减速时间为

第5阶段台车从vmin以加速度-amax减速到0,此阶段和第3阶段所组成的运动过程与第1阶段完全对称,满足t1=t3+t5,以保证运行效率最大化.
第2阶段台车以最大速度vmax匀速运行,在最终能准确定位的前提下,应保证运行时间尽可能长,从而提高运行效率.系统通过激光测距仪来实时判断当前台车位置与制动距离db的关系,当与目标位置的距离小于db时,进入第3阶段.由于d1,db可通过离线计算获取,从而得减速时间为

第4阶段目的是为了台车减速过程的平稳过渡,以保证定位终点无来回摆动的现象发生,因此如何确定d4从而确定db是台车精准定位的关键问题之一.
为解决由于轨道的湿滑程度在不同时段和季节存在差异,导致制动距离db发生变化的问题,利用轨道状态评估结果设计自适应控制策略,动态调整下一阶段运行的vmax.由式(4)可知,σ越大,表示轨道状态越差,滑行距离越长,此时应该减小vmax,从而保证台车制动时能在设定的db内准确定位.为了简化工业现场控制并不失一般性,下一阶段的最大速度vm表示为

车间内利用可编程逻辑控制器(programmable logic control,PLC)和变频器共同控制行车,变频器内部集成的直接转矩控制系统(direct torque control,DTC)本身有电流环、转速环等结构,控制时存在调节时间ts.通过在锌电解车间反复实验,发现系统运行过程中响应速度慢,所规划的速度轨迹难以实时跟踪上实际速度轨迹而造成明显的滞后现象.基于运输效率的考虑,DTC 内部的转速环选择PI控制器来保证加速时间最短.基于以上原理,台车达到设定速度需要经过动态过程和稳态过程,经过ts才能满足稳态误差要求.
定义台车运行过程中的实际速度为vr,当前位置离目标位置的距离为dr.受工业行车运行特性的影响,第3,4阶段实际行驶的距离往往受轨道状态、轨迹跟踪时间等外部因素的干扰,导致分级制动阶段的距离不确定性大大增加.为确保台车在分级制动阶段表现出更好的性能,引入最小安全距离的概念,表示如下:

其中:d41表示台车从第3 阶段vmax减速到第4 阶段vmin时,vr最终稳定到vmin时所行驶的距离,此过程称为低速调节过程(图10中的局部放大部分可反映实际工业行车的速度调节特性).d42定义为最小安全距离,表示台车以速度vmin匀速行驶的距离,目的是为了预留一定的距离裕量.

定义ds为安全减速距离,表示台车经低速调节过程后离目标位置的距离,通过ds来确保台车准确定位.实际运行过程中,台车允许的vm,db存在较大的差异,不能保证每次的db相同,因此提出制动距离自适应的方法.
通过激光测距仪实时获取台车低速调节过程后的dr,如果此时dr>ds,则下一阶段运行的制动距离db更新为

反之更新为
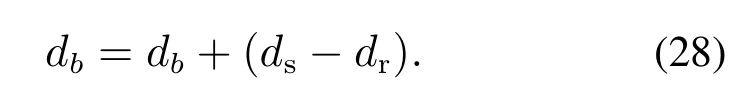
理想情况下台车从vmax减速到vmin,第4阶段过渡时间趋近于0,然后直接进入第5阶段斜坡减速完成制动并准确定位,使每一次dr≈ds,此时运行效率最佳.自适应在线更新轨迹参数的步骤如下:
步骤1进行参数初始化,根据现场实验数据确定vmax,vmin以及db,进而确定d42,d5以及ds,通过现场测试,初始db可设置一个较大值,以保证台车安全运行;
步骤2利用激光测距仪对dr实时在线检测,当dr>db时,台车以vmax运行,反之,台车通过PLC直接给定vmin运行;
步骤3当vr经过低速调节过程后稳定为vmin时,记录此时的dr,比较dr与ds,从而进行下一阶段的决策;
步骤4当dr>ds时,按式(27)更新db,此时可推断出当前轨道状况良好,制动距离偏长,应将其减小.反之,按式(28)更新db,此时可推断出当前轨道状况不佳,制动距离偏短,应增加制动距离;
步骤5基于轨道状态评估系数σ,按式(24)更新vmax,按式(27)-(28)分别更新db.通过自适应调节vmax和db来动态更新轨迹的参数,直到台车的定位效率和精度达到实际生产的要求,并且摆角稳定在安全范围内.
4 仿真实验
为验证所提方法的有效性,使用MATLAB平台进行数值仿真.考虑实际情况,仿真过程中设定参数

根据所设参数,应用本文提出的在线轨迹规划方法计算运动过程各阶段的参数如表1所示.

表1 仿真参数表Table 1 Simulation parameter table
由表1可知,规划了3条轨迹曲线.轨迹1,2,3分别表示初始轨迹、自适应学习db后的轨迹以及自适应学习vmax和db的轨迹,并计算出每个阶段运行的时间.
由图5可知,所规划的轨迹1以最大速度运行,初始制动距离设为10 m,此时d4≫d42,dr>ds,t4过长,最终总耗时26 s.假设轨迹1轨道状态良好,σ=0,根据此条件对下一周期的轨迹进行在线更新,经过第1次运行的制动距离参数学习后,第2次运行的制动距离db从10 m减少为8.5 m,得到轨迹2.由轨迹2可知,学习到了最佳制动距离db运动周期结束后dr≈ds,总时间仅为23.75 s,较第1次运行缩短了2.25 s,提高了运行效率.轨迹3轨道状态不佳,σ=0.15,根据式(24)(27)-(28)计算下一运行过程的vmax以及db,规划最新的轨迹曲线,结果表明dr≈ds,最终的运行时间仅为25.15 s,与运行效率最高的轨迹2相比,该轨迹不仅能保证在轨道状态改变的前提下稳定运行,还不会降低系统的运行效率.

图5 3种轨迹速度曲线Fig.5 Three trajectory speed curves
由图6可知,3条轨迹的定位结果表明台车最终都能准确停在目标位置,且轨迹2、轨迹3与轨迹1相比,效率更高,验证了所提方法的有效性.

图6 3种轨迹距离曲线Fig.6 Three trajectory distance curves
由图7可知,轨迹1的摆角在第1阶段以角速度wn自然摆动,经过几个周期后,进入第2阶段,此时摆角接近于0,而在分级制动阶段,摆角会随着加速度的切换而变化.轨迹2与轨迹3由于改变了某些阶段的运行时间,导致摆角小范围增加,但3种轨迹在整个过程中的有效载荷摆角均小于0.1°,始终保持在安全范围之内.

图7 3种轨迹负载摆角曲线Fig.7 Three trajectory load swing angle curves
仿真结果表明,台车每完成一个运动周期后会根据轨道的状态,学习新的σ来对下一周期的运动进行决策,得到新的vmax和db,以保证自适应在线轨迹规划方法每次运行的效率最高且有效消摆.
5 工业现场测试与应用
将提出的自适应在线轨迹规划方法应用到某大型国有企业的锌电解车间,实验对象为工业5+5t行车.
本文方法下的行车自动定位控制系统在锌电解车间投运前,行车由经验丰富的工人手动操作,人工驾驶存在着劳动强度大、工作效率低和定位精度差等缺点,且人工长时间工作后会产生疲劳,可能导致非常危险的错误操作,造成安全事故.此外,培训有经验的工人耗时长、花费高.
为克服以上缺点,经过与某大型国有企业的长期合作和共同努力,所提方法已成功应用于锌电解车间,所开发的行车自动控制系统(图8)具有运行效率高、安全性高、定位精度高的特点,解决了人工驾驶行车存在的诸多问题.

图8 行车自动控制系统Fig.8 Automatic crane control system
该系统主要分为硬件和软件两部分.硬件部分包含劳易测的AMS 348i系列激光测距仪和科瑞的CXGA58E编码器,用于获取大车、小车和起升装置的位置信息;3台ABB的ACS880变频器,对大车、小车以及起升装置进行运动控制,西门子S7-1500的PLC、输入输出模块以及TP1500触摸屏,来完成系统控制和信息交互.此外还有三相异步电机(45 kW 80 A)、机械结构等.软件部分包含控制算法的实现以及行车信息的监控,在PLC平台上写入控制算法并与上位监控软件进行信息交互,监控系统状态.
以行车的大车三相异步电机为例,变频器的控制信号由PLC通过PROFINET协议进行设定,将现场参数代入式(5)-(6),可知电机额定转速1460 r/min与台车速度2.5 m/s相对应.但基于安全性的考虑,台车实际允许的最大速度不能超过机械允许的最大速度vml=2.1 m/s.现场实验过程中l=2 m,减速比k=13.64,车轮半径r=0.3 m,初始db=10 m,ds=1.2 m.经过现场长时间测试,发现轨道状态良好时db自适应调整为7 m左右.测试过程中发现当vmin过大、d42过小时,台车会在定位终点附近来回运动,长时间后才能稳定,给驾驶人员带来潜在风险.当vmin过小、d42过大时,会导致运行效率降低,从而增加车间人员的劳动强度.经过对锌电解行车安全减速距离的反复测试,最终确定vmin=0.2 m/s,d42=0.5 m时定位效果最佳.
为验证本文方法的性能,将该方法下的自动驾驶与人工驾驶进行对比实验,选择运行起点为电解槽的1槽位置,终点为取阴极板位置,pd=55.407 m,保证定位精度均在5 mm以内.由图9可知,自动驾驶在40.5 s左右到达目标位置,而人工驾驶在46.2 s左右才能完成定位任务,可见本文提出的轨迹规划方法定位效率更高.由图10可知,两种驾驶情况下加速阶段基本一致,匀速阶段由于轨道不同位置的平整程度各不相同,速度在2.1 m/s附近上下波动,符合工业现场运行状态.人工驾驶行车减速制动阶段耗时19.5 s,为了保证最终能准确定位,通常提前减速来保证安全制动,所以减速曲线较为平缓,但同时降低了运行效率.自动驾驶行车减速制动阶段耗时14.1 s,论文所提出的方法会根据轨道的状态自适应调节最佳制动距离来获取最佳制动时机,与人工驾驶相比,运行效率提高27.7%.此外,现场通过人工手持激光测距仪获取当前位置离行车有效载荷锌极板的距离,根据其与行车位置的距离偏差和绳长的比值来计算摆角,实验证明运行过程中人工测试的摆角小于1°,始终保证在安全范围内.

图9 距离曲线对比Fig.9 Comparison of distance curves
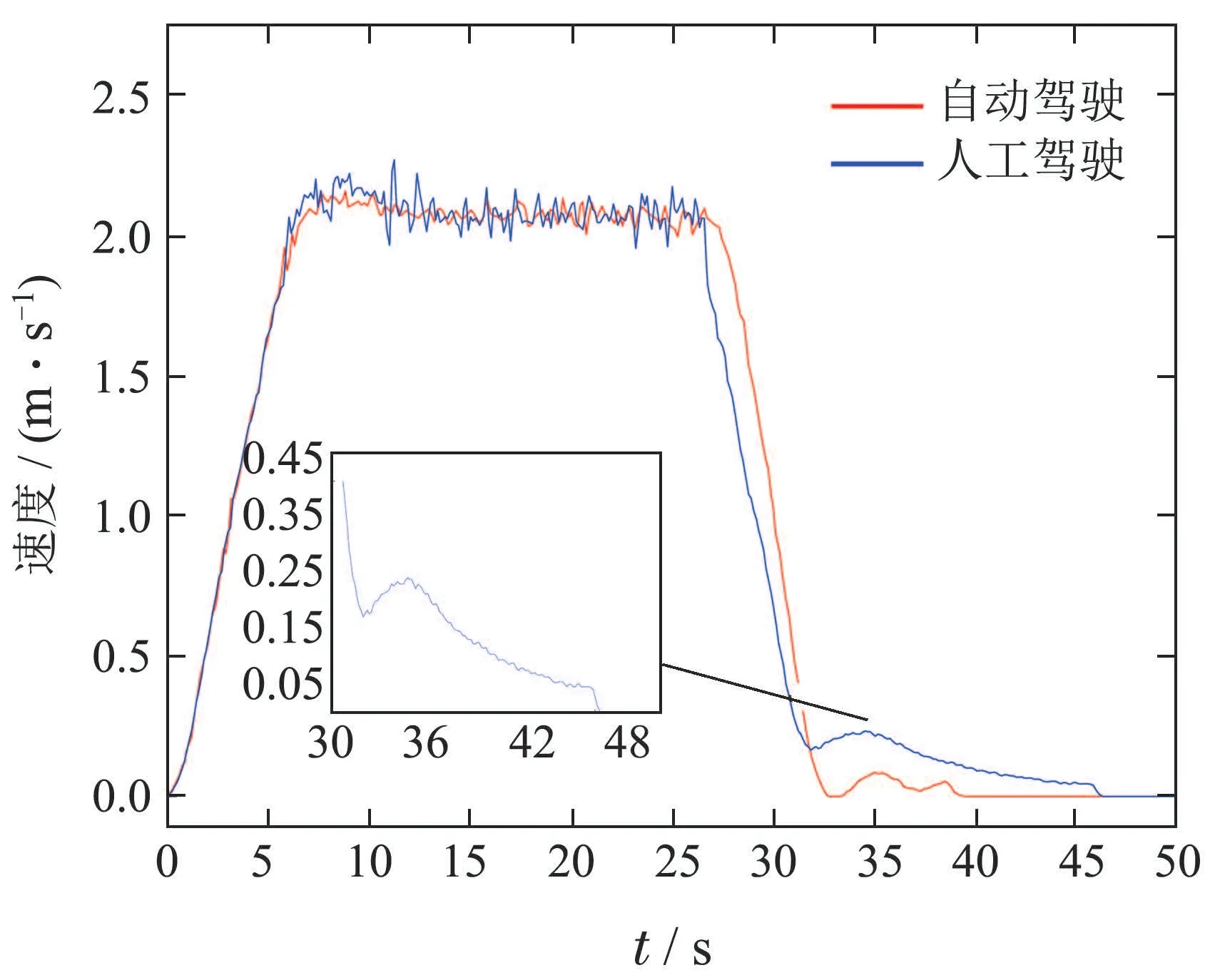
图10 速度曲线对比Fig.10 Comparison of velocity curves
锌电解车间内每个槽共60块极板,每个工作班吊运槽中的30块,其吊运工艺流程简述为:首先利用行车将电解槽内的极板吊运至自动剥锌机处进行剥锌,然后将剥锌完毕的极板吊运回电解槽内重新电解.基于以上工艺,选取车间常用吊运位置进行实验,如表2所示,实验1-3分别表示起点为取阴极板、1号槽、人工剥锌,终点为27号槽、放阴极板、5号槽的位置,重复吊运5次的平均效果.实验a表示一个工作班内60次吊运的平均效果.tb1,tb2分别表示自动驾驶和人工驾驶减速制动阶段多次测试的平均运行时间,η=表示本文方法下所提高的制动效率,e1,e2分别表示自动驾驶和人工驾驶多次测试的平均定位误差.
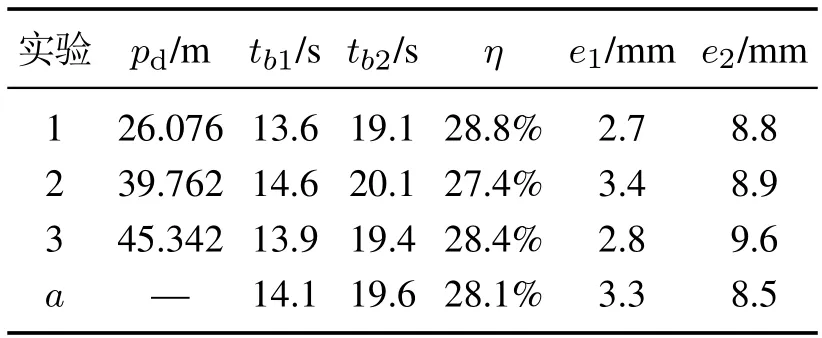
表2 自动与手动定位效果对比Table 2 Comparison of automatic and manual positioning effects
表2中人工驾驶的定位误差基本在9 mm左右.但车间环境恶劣时,也存在着行车在目标位置来回摆动的现象,导致调节时间过长或定位误差过大.本文方法下的自动驾驶方式定位精度在3 mm左右.以上实验结果表明,本文所提方法提高了行车的定位效率与精度,具体而言,优化的时间主要体现在分级制动阶段,使得调节时间变短.此外自动驾驶还降低了操作人员的劳动强度,且运行效果明显优于人工驾驶.
6 结论
本文针对锌电解车间环境恶劣,其行车速度轨迹跟踪滞后,现场酸雾、水蒸气等因素会引起行车打滑,导致其制动后滑行距离不可控,定位效率低且误差大的问题,提出一种基于轨道状态评估的自适应在线轨迹规划方法.针对车间内轨道状态无法评估的问题,提出轨道状态评估方法并建立锌电解行车模型,解决了传统行车模型无法直接适用于电解车间的问题.针对减速制动阶段人工驾驶行车过于依赖经验而导致制动效率低的问题,根据行车离目标位置的实时距离来优化不同阶段的运行时间,确定分级制动阶段的最佳制动时机,并实时更新轨迹的有关参数,提高制动效率.现场实验结果表明,自动驾驶与人工驾驶相比,定位精度更高,且每个减速制动阶段,制动效率平均提高28%,很好的满足了当前锌电解车间对定位精度和定位效率的要求,对锌冶炼过程智能化的发展具有重要意义.未来将考虑纳入最优规划的思想,进一步提高行车的运行效率,并在工业中进行大规模的推广应用.

