随机需求车辆路径问题的价值逼近在线决策

张晓楠张建雄

(1.天津大学管理与经济学部,天津 300072;2.陕西科技大学机电工程学院,陕西西安 710021)

1 引言

车辆路径问题(vehicle routing problem,VRP)是运筹学和组合优化领域中的热点[1-2],实际运营过程中存在很多不可预知性[3].近年来,移动互联和计算机技术的应用发展使得配送系统中不确定信息的实时共享与交互成为可能.在这一背景下,如何利用这些实时共享和交互的数据信息,做出即时有效的动态路径决策,是一个值得研究的问题.尤其在实时物流快速发展的今天,这一问题的解决显得更为迫切[4-5].随机需求车辆路径问题(vehicle routing problem with stochastic demand,VRPSD)是应用最为广泛的不确定车辆路径问题,因客户需求随机且确切需求信息往往在车辆到达客户点时才能获知,在应急物流、废弃物回收等领域有应用价值[6-7].本文以这一问题为例展开研究.

两阶段法是求解VRPSD的常用方法,即在客户需求未明的情况下先设计一个预优化方案,车辆严格按照预优化方案执行,当车辆到达客户获知实际需求后,为避免发生因实际车载量不能满足客户需求而导致路径失败,对车辆是否返回配送中心补货进行实时调整.如,曹二保等[8]研究需求服从模糊分布的VRP,建立可信度约束模型,并得出,当可信度阈值为0.6时的预优化方案最佳;Zhu[9]考虑车辆遭遇失败才返回配送中心补货(反应式策略),研究同时配集货VRPSD;Luo[10]考虑车辆可在失败点前返回配送中心补货以避免路径失败(主动式策略),研究成本与重量相关的VRPSD;范厚明[11]、王征等[12]、宁涛等[13]考虑在车辆遇到路径失败时重新求解重调度或扰动恢复模型,对失败点及未服务客户优化得到一条符合当前状态的计划路径(重调度策略).然而,在这些策略下,车辆需严格遵守预优化方案的客户分区和服务顺序,全局优化能力受限.另外,这些策略忽略了实时共享和交互的信息价值,决策缺乏实时动态性和适应性.

在线方法主要用于处理决策者无法掌握问题全部信息的情形下必须进行实时决策的一种方法[14-16].相较于两阶段法,在线方法不受预优化方案限制,且利用了信息和数据的实时共享和交互价值,强调在每个决策点更新当前实时状态,并即时给出在线决策,为不确定VRP的求解提供了新视角[17].目前,关于VRPSD在线决策的研究已经展开,如,Secomandi和Margot[18]针对单车辆(single-vehicle VRPSD,SVRPSD),建立马尔可夫决策模型(Markov decision process,MDP),设计一步Rollout算法求解,其中,采用精确后向递归法估算期望未来成本,引入(partitioning heuristic,PH)和(sliding heuristic,SH)减少状态空间.Novoa和Storer[19]提出两步Rollout算法求解SVRPSD,其中,采用蒙特卡罗模拟算法替代精确后向递归法,引入最佳阈值减少动作空间.Bertazzi和Secomandi[20]结合后向递归和前向递归以快速估算期望未来成本.此外,一些多车辆(multi-vehicle VRPSD,MVRPSD)被扩展.如Goodson等[21]建立多车辆(multi-vehicle MDP,M-MDP),并将MVRPSD分解为多个SVRPSD以克服MVRPSD的维度灾,设计混合Rollout算法求解每个SVRPSD;为加强车辆间的资源共享,文中引入动态分区策略在每个决策点重置客户分区.Goodson等[22]在文献[21]的基础上,考虑主动补货策略,改进决策前Rollout算法求解每个SVRPSD,并引入命题去修剪状态空间.然而发现:1)维度灾问题是制约在线决策的主要瓶颈,现有研究多关注SVRPSD的在线决策,涉及MVRPSD时也是考虑将其分解为单个SVRPSD求解;2)MDP是刻画VRPSD动态特性的常用模型,一般采用Rollout算法求解.然而,Rollout算法是一种仿真优化算法,需要在每个决策点建立在线状态决策树,当问题复杂时,决策实时响应能力不足.

价值逼近算法(value approximation iteration,VAI)是指通过环境和行为的交互学习,找到状态-动作和期望未来价值的映射关系,进而提取最优策略的一种方法,属于强化学习范畴.近年来,该算法被用于求解动态库存问题[23]、单车辆动态VRP[24]、随机背包问题[25]等,并表现出良好的决策质量和实时响应能力.

基于此,本文考虑多车辆同时在线,基于VAI展开对MVRPSD的在线决策研究.首先,利用MDP刻画问题的动态特性,建立M-MDP模型,并引入可信度约束和邻域半径减少策略修剪动作空间.其次,替代分解机制,设计价值逼近算法直接求解MVRPSD,即在价值逼近算法的框架下,采用基函数估计期望未来成本,并将求解过程分离为离线训练和在线决策两个环节,基函数权重被离线训练,训练结果随后用于在线决策,减少在线决策时间,同时,在算法中设计邻域半径的动态更新机制.最后,实验选取了最佳基函数集合方案;将本文方法与其他策略和算法对比,验证了本文方法的有效性;开展了“西安市未央区垃圾回收”和“随机需求可动态揭露的MVRPSD”的扩展测试.研究成果可扩展到其他多车辆VRP在线决策.

文章结构如下:第2节给出了MVRPSD和在线方法的描述,并建立了M-MDP模型;第3节给出了算法设计和基函数集合;第4节为算例验证和结果分析;第5节是两个扩展测试,探讨了本文方法求解VRPSD扩展问题的鲁棒性,以及随机需求被提前揭露的价值;第6节总结了研究结论和展望.

2 M-MDP模型

2.1 MVRPSD的问题描述

MVRPSD可描述如下:配送网络有完备的有向图G=(N,E),所有点集合N=0∪N0,0表示配送中心,客户点集合N0={1,2,···,n};边集合E={(i,j)|∀i,j ∈N},两节点i,j之间对应距离成本d(i,j);m为车辆集合M={1,2,···,φ}的任一车辆,车容量为Q.客户节点i(i ∈N0)存在不能提前获知的需求,在车辆到达之前仅已知波动区间=(ξi1,ξi2,ξi3),ξi1=max{0,ξi2(1-dod)},ξi3=ξi2(1+dod),dod表示需求波动的动态度.当车辆到达客户点i获知实际需求后,不确定需求更新为已知需求ξi.假设车辆从配送中心出发,服务一系列的客户后回到配送中心,中途允许返回配送中心补货;所有客户均要求被完全服务,且每个客户只能服务一次,在遭遇失败客户时,允许分离失败客户的需求;在每个客户点,车辆总是尽最大可能服务客户;每辆车在服务中不考虑等待;正在去往下一客户的在途车辆不允许中途改变行程.目标是规划车辆行车和补货路线,使得期望总旅行成本最低.

2.2 在线策略

本文将在线方法下的决策规则称为在线策略.以图1为例对两阶段法(反应式策略、主动式策略、重调度策略)和在线策略进行图示分析,实线代表预优化方案,虚线代表调整路径.该配送网络包含6个客户和2辆车,存在预优化路径0-1-3-5-0,0-4-6-2-0,如图1(a)所示.

1) 反应式策略图1(b).车辆按照预优化方案执行并直接拜访下一客户,当遭遇失败时(客户3和6),车辆返回配送中心补货后重新回到失败点继续服务.整个过程车辆服务客户集合和服务顺序不变.

2) 主动式策略图1(c).在反应式策略基础上,允许车辆在失败点(客户3和6)前返回补货.理论上,该策略优于反应式策略(依据三角形三边原理),但实际上,由于无法提前准确获知执行过程的失败点,对失败点的不当预判断会导致多余的返回.

3) 重调度策略图1(d).以车辆1在客户3遭遇失败、车辆2正服务客户4为例,该策略为失败点和未服务点(客户3,5,6,2)重新规划路径,可看作开放的多中心VRPSD.以新调整方案3-0-3-5-6-2-0和4-0为例,车辆1从失败点3回到配送中心补货后服务客户3,5,6,2;车辆2服务完客户4则结束服务.该策略的实时响应能力不足,且当需求波动大时,重优化次数较多.

4) 在线策略图1(e).决策不受预优化方案限制,当车辆到达客户揭露实际需求后,系统更新当前状态,并做出下一步动作决策.图中以车辆在配送中心做出服务客户1和客户4的决策为例.

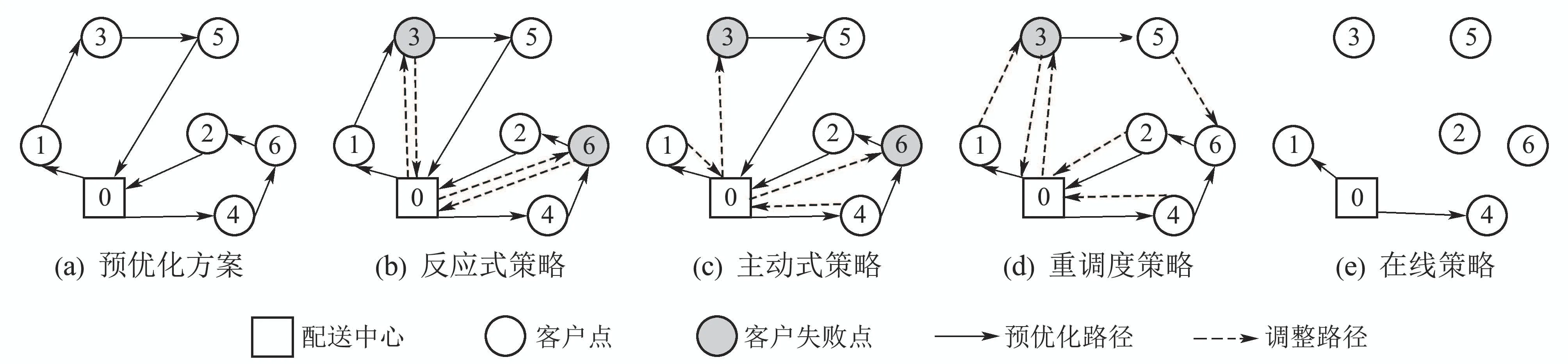
图1 不同路径策略分析示例Fig.1 Different route-recourse policies

2.3 马尔科夫决策过程

利用MDP刻画MVRPSD的路径在线决策过程,建立T+1阶段的有限时域MDP.每个阶段对应车辆到达客户获知实际需求后需要做出决策的决策点k,k ∈[0,T].在每个决策点k,系统更新为当前状态sk,受当前状态驱动在线做出路径决策ak,即“选择下一服务客户”和“在拜访下一客户前是否返回配送中心补货”.目标是使得执行完所有决策之后的路径方案逼近完美信息下的离线最优策略.

2.3.1 参数设置

为便于MDP模型的建立,设置如下参数:

2.3.2 模型建立

1) 系统状态.

图2 状态转移过程示例Fig.2 An example of state transition

4) 目标函数及处理.

模型的目标函数是追求一个动作序列π ∈Π,使得执行完所有决策的总旅行成本最小,即

参考文献[24],本文引入贝尔曼方程,定义每个决策点的成本价值为当前立即成本和期望未来成本之和.那么,在每个决策点k,最佳动作序列π∗选择在该决策点的当前成本和期望未来成本之和最小的动作为最佳行动即

3 价值逼近算法设计

本文的算法是在价值逼近算法的框架下,从以下几个方面设计以提升动态MVRPSD的求解质量和实时响应能力:1)采用基函数估计期望未来成本,通过构建合适的基函数集合,提高决策质量;2)分离求解过程为离线训练和在线决策两个环节,基函数的权重被离线训练更新,训练结果用于在线决策,减少在线决策时间;3)设计邻域半径Nradius的动态更新机制以选取合适的取值,从而控制动作空间(sk).

3.1 采用基函数估计期望未来成本

基函数集合通常选取能够刻画MVRPSD问题路径决策的成本结构特征构成,如车辆数、车辆剩余载重、当前车辆位置等.通过提取合适的基函数集合,准确描述决策后状态的期望未来成本V(),其实质就是“输入决策后状态提取基函数特征→输出期望未来成本估计值V()”.

3.2 选择最佳行动

为了求解行动空间最小值问题(式(12)),本文引入估计值()替代V().因本文的价值逼近算法分为离线训练和在线决策两个环节,下面分别给出了二者的行动决策公式:

1) 离线训练过程:定义ρ为离线模拟迭代次数(也就是训练第ρ个离线模拟样本ωρ),则第ρ个离线模拟样本下第k个决策点的最佳行动为

基于此,每个决策点k的行动空间选择问题转化为确定型最小值问题,计算时效性得到了提高.

3.3 基函数的权重更新

3.4 邻域半径的动态更新

3.5 算法整体框架

图3 算法流程框架Fig.3 Framework of the proposed algorithm

3.6 几种基函数集合的设计

表1 9种基函数集合Table 1 Nine sets of basis functions

4 算例验证和结果分析

因缺乏MVRPSD标准算例,本文改进标准CVRP算例生成MVRPSD测试算例(CVRP算例来源:http://neo.lcc.uma.es/vrp/vrp-instances/capacitated-vrp-instances/),即在标准CVRP基础上,改进动态度dod和车容量Q,令客户需求服从任意分布.本文共生成29个MVRPSD算例,涉及客户规模n=3～150;动态度dod=50%,100%,200%,500%;车辆数φ=1～4.需要说明的是,当算例规模n小于数据集给定的客户规模时,仅选取前n个客户,如“C5-d50-V1”表示客户规模n=5,dod=50%,φ=1,来源于算例An32-k5的前5个客户.

采用MATLAB 2016a编程,操作系统为windows 10,电脑内存为8 G,CPU 为Intel i7-6700,主频3.40 GHz.参数设置为:初始邻域半径=5,步长α针对不同算例和基函数特征取值不同.举例,算例“C30-d50-V3”在集合φ9下的步长方案为α={α1,α2×ones(1,m),α3×ones(1,m)},文中讨论4种取值(α1,α2,α3)={(0.1,0.1×10−5,0.1),(0.01,0.1×10−5,0.01),(0.001,0.1×10−5,0.001),(0.1,0.1×10−6,0.1)},最终取(α1,α2,α3)=(0.001,×10−5,0.001).另外,基于文献[8]“可信度阈值为0.6的预优化方案最佳”的结论,本文的预优化方案取文献[28]求解得到的可信度阈值为0.6的方案,模型和算法有效性已在文献[28]论证.其他参数设置如下:离线样本数Max-N=10000,最大持续迭代数Max-B=200;更新到后仍需训练的样本数Max-C=6000.在线样本数Max-M=1000.阈值eps1=0.005和eps2=0.01.

4.1 最佳基函数集合选择

为选取合适的基函数,本文应用回归分析方法计算9种基函数集合的R2值,并结合在线学习得到的总旅行成本和完美信息离线最优策略下的总旅行成本的误差百分比,最终综合分析选取合适的基函数集合.由于R2值以所有状态及其实际成本价值拟合,因此,这里仅应用可以精确求解的8个小算例进行测试讨论.客户规模为C3和C5;动态度50%,100%,200%,500%;车容量Q=100.对于C3的算例而言,每个样本约得到96～2400个状态;对于C5的算例而言,每个样本约得到11520～67470个状态.因此,1000个C3的在线样本得到约96000～2400000个状态,1000个C5的在线样本得到约11520000～67470000个状态.

表2给出了R2和误差(%)的统计值.可以看出,R2值和误差负相关,即随着R2值的增加,误差减小.另外,这种负相关存在一定偏差,如φ4和φ5;的二进制设置效果体现在φ4和φ6的对比中;权重分行设置的效果体现在φ5和φ7的对比中.综合来看,集合φ9综合性能最好,能以平均2.42%的误差逼近完美信息下的最优策略,说明:1)预优化方案中包含对在线决策有利的基因,在基函数中加以利用会提高动作的竞争性;2)选取合适的基函数集合利于逼近效果,但若特征过多反而会使得逼近效果下降,如φ8.

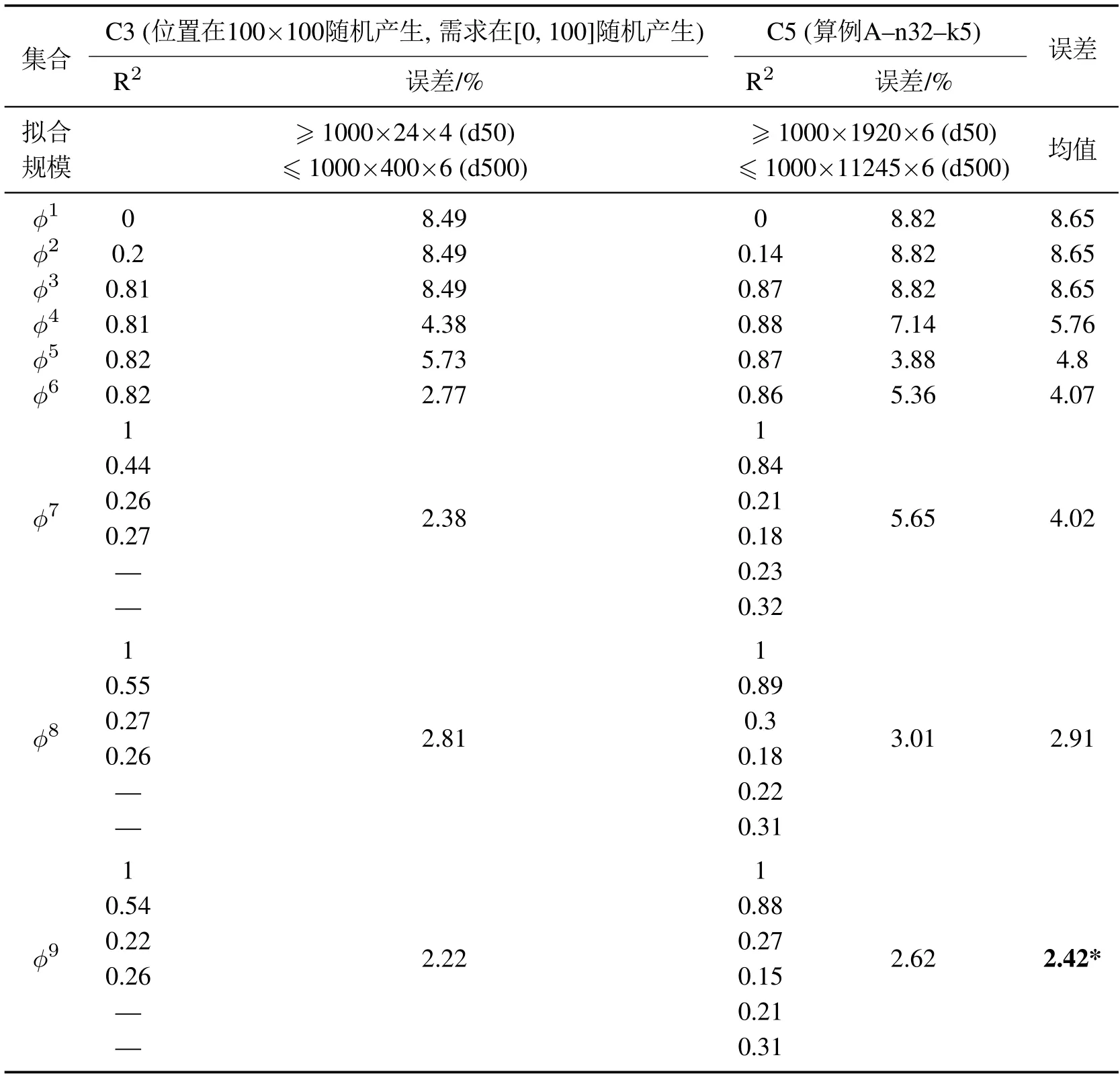
表2 基函数的R2和百分比误差Table 2 R2 and gap of the sets of basis functions

4.2 策略有效性验证

在最佳基函数集合φ9设置下,进一步讨论本文方法相较于现有常用快速反应策略(反应式策略、主动式策略)的有效性.这里应用小规模、中规模和大规模共22个算例进行测试,涉及客户规模C5/C10/C20/C30/C50/C80/C100/C120/C150,车辆数V1～V4,动态度50%,100%,200%,500%.

表3给出了每个算例在3种不同策略下的实际误差百分比.因测试算例无法精确计算,表中基准解为预优化方案的计划成本,%Dev是每个算例下1000个在线样本的实际总旅行成本和基准解的误差百分比均值;MinMaxMean是1000个在线样本的最小值最大值平均值;

加粗用以标记3个策略的最优成本,*标记在线学习成本低于基准解的情况.

由表3可以看出,本文策略求解22个算例的平均误差是10.75%,低于反应式策略的14.79%和主动式策略的14.42%,较反应式策略和主动式策略性能提升约3%-4%左右;其中,19个算例的整体运营效果优于反应式策略和主动式策略,5个算例的整体运营效果比基准解更优(如算例C10-d50-V2 的整体运营成本397.18<基准解405).另外,从求解时间看,本文的方法求解时间较快,每个样本的在线执行时间平均约0.33 s,单个决策点的决策时间约0.01 s.

表3 不同路径策略结果对比Table 3 Results comparisons on different route-recourse policies

综上,本文算法是求解MVRPSD的有效算法,在决策精度和实时响应能力上均表现较好,不受预优化方案的路径安排局限,会选择更好的行动执行.

4.3 算法有效性验证

为进一步评估本文算法和常用的Rollout算法的性能区别,表4以算例C30-d50-V3为例对比了本文算法和同样求解MVRPSD的文献[22]的Rollout算法.结果显示:相较Rollout算法,本文算法在决策精度和实时响应能力上均有优势,且实时响应能力优势明显,如,本文算法执行一个在线样本(执行完该样本下所有决策)的决策时间为0.36 s,而文献[22]的Rollout算法耗时6.97 s(作者将MVRPSD分解为多个SVRPSD求解,样本规模取P=30).当P增加时,Rollout算法耗时更多.

表4 算例C30-d50-V3的结果对比Table 4 Results comparisons on Instance C30-d50-V3

图4 离线训练进化曲线Fig.4 Value convergence curve in offline simulation phase

4.4 敏感性分析

1) 多车辆问题的影响.

为说明问题复杂度的影响,图5展示了算例C10/C20/C30/C50在单车辆和多车辆问题上(V1和V3)的单个样本在线决策时间和决策空间¯A(sk)对比.可以看出:从单车辆问题扩展至多车辆问题时,决策时间和决策空间呈指数级增长.另外,因已引入邻域半径减少策略,图中的指数级增长已被一定程度的缓解,实际的指数增长趋势较图中展示的更明显.这也说明了本文考虑多车辆问题的复杂度,以及现有文献多集中于研究单车辆问题的原因.

图5 决策时间和空间对比Fig.5 Comparisons on CPU and the size of decision space

2) 邻域半径减少策略的影响.

图6是算例C10/C20/C30/C50在有无邻域半径减少策略设置下,多车辆问题(V3)的单个样本在线决策时间和决策空间¯A(sk)对比.可以看出,邻域半径减少策略对提高求解效率效果显著,且随着问题规模增加,显著性增加.

图6 有无Nradius下,多车辆(V3)的决策时间和空间对比Fig.6 Comparisons on CPU and the size of decision space with/without Nradius setting for the three-vehicle case

3) 最佳邻域半径取值.

表5 的取值Table 5 Value of

表5 的取值Table 5 Value of

另外,图7以M30-d50-V3为例展示Nradius的动态更新过程.可以看出:随着邻域半径Nradius增加,算法性能增强,当增加至最佳取值时(最佳取值=11),算法性能趋于平稳,说明动态更新机制合理有效.

图7 Nradius的动态更新过程Fig.7 Dynamic update process of Nradius

5 相关扩展

5.1 扩展一:西安市未央区垃圾回收实例(允许多行程且带时间窗限制的MVRPSD)

MVRPSD的应用场景多为应急物流、废弃物物流等领域,本文进一步选取西安市未央区某垃圾压缩站及其覆盖的30个小区的生活垃圾回收路径优化实例进行测试.与常规MVRPSD问题不同,在垃圾回收过程中,因小区分布较为密集,且回收量较大,回收车辆在服务路径中会多次往返取送,且存在总服务时间不超过8小时的时长限制.因此,该问题为允许多行程且带时间窗限制的MVRPSD.假设各小区的服务时间为0.25 h.预优化方案是一条满足车容量偏好值0.6且允许多行程和有时间窗约束的预优化路径.表6是位置坐标和产生量的相关数据,其中,垃圾产生量以2019年西安市人均生活垃圾产生量乘以小区人口并按一天回收3次均分计算,车容量取16 t.

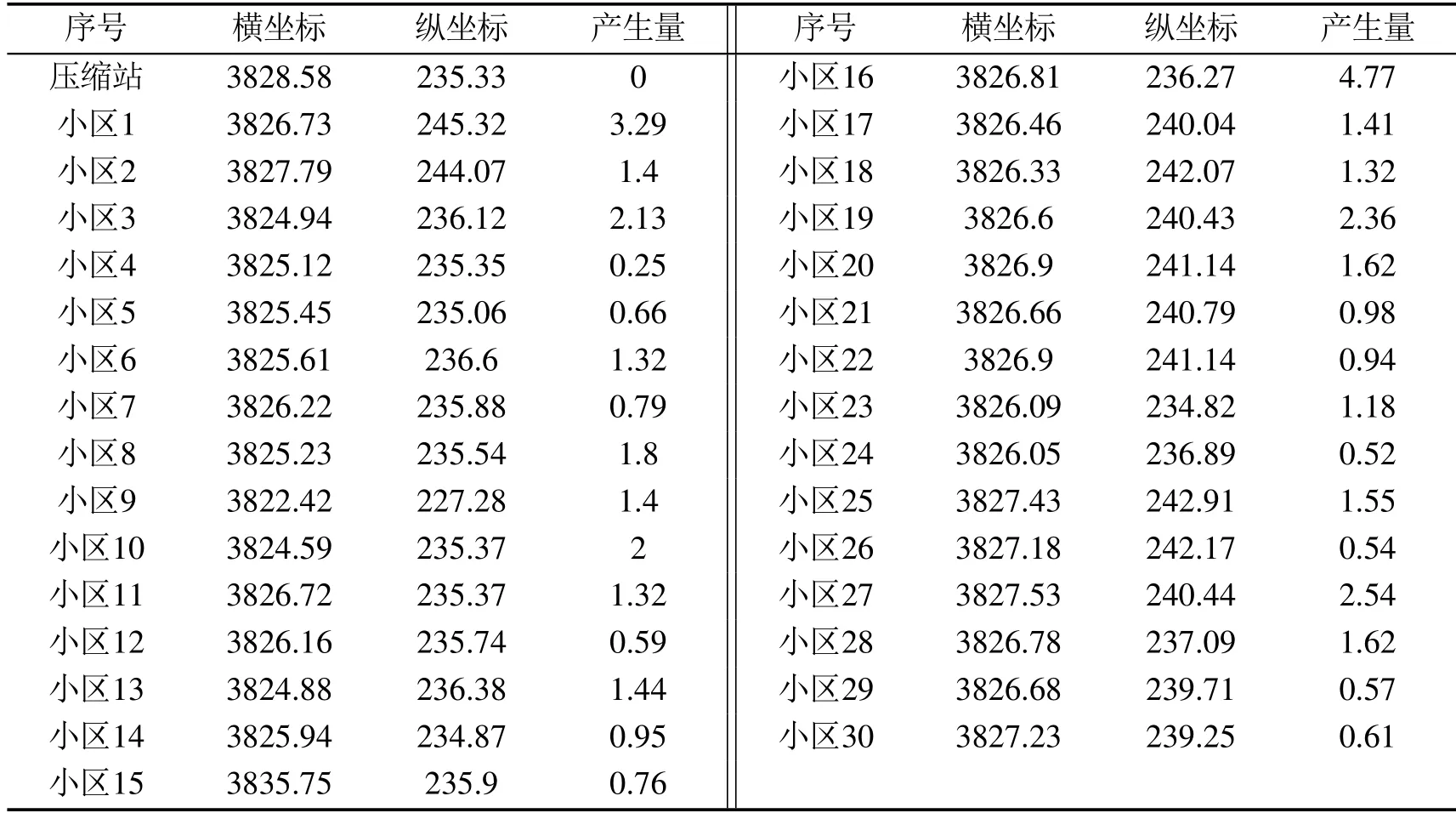
表6 数据表Table 6 Data set

表7是不同动态度下反应式策略、主动式策略和在线策略的结果对比.结果表明,求解允许多行程且带时间窗限制的MVRPSD问题时,本文方法的性能表现仍优于反应式策略和主动式策略.

表7 3种策略的决策结果(实际成本)对比Table 7 Results (actual costs) comparisons under three policies

5.2 扩展二:随机需求可动态揭露的MVRPSD

在上述的所有测试中,本文参考常规VRPSD特性,假设MVRPSD中客户实际需求信息只有在车辆到达客户后才获知.实际上,随着计算机技术的发展应用,客户的实际需求可能提前揭露,这就将MVRPSD扩展为随机需求可动态揭露的MVRPSD.具体如下:定义随机需求的揭露时间ui服从参数为的泊松分布.那么,更新为:若未被到达且满足ui >tk,表示客户未被揭露,=?;若未被到达且满足ui≤tk,表示客户i虽未到达但已被揭露,=ξi;若被完全服务,则=0;若被部分服务,则=σ.

表8 不同的决策结果(实际成本)对比Table 8 Results (actual costs) comparisons under differentvalues

表8 不同的决策结果(实际成本)对比Table 8 Results (actual costs) comparisons under differentvalues

6 结论

本文针对MVRPSD问题,研究提出了基于价值逼近的在线决策方法.首先,考虑多车辆同时在线,以总成本最小为目标函数,建立了相应的马尔科夫决策模型,并引入可信度约束和邻域半径减少策略缩减动作空间,提高求解效率;其次,采用价值逼近算法求解模型,设计基函数估计期望未来成本,并将求解过程分离离线训练和在线执行过程,其中,基函数权重被离线训练,训练结果用于在线决策.最后,实验选取了最佳基函数集合,测试多组算例验证了本文方法的性能,并进行了算法敏感性分析和扩展测试.

主要结论如下:1)集合φ9的综合性能最好,说明,预优化方案中包含对在线决策有利的基因,加以利用会提高决策的竞争性;2)相较于反应式和主动式策略,本文的在线策略性能良好,甚至可能产生比预优化方案更好的方案;3)相较于Rollout算法,本文方法能直接求解多车辆VRPSD,决策性能在决策精度和实时响应能力上均存在优势,尤其实时响应能力上优势明显;4)邻域半径减少策略的应用能够为客户规模超过11的MVRPSD算例缩减行动空间,并保证求解精度,且本文所设计的邻域半径动态更新机制合理有效;5)不确定信息的提前揭露利于决策精度的提高,但揭露时间较迟时效用不大.

后续研究可扩展到多目标MVRPSD、即时配送、同城配送的在线决策.另外,本文方法与其他方法的结合,如与非参数价值逼近的结合,与分支定界/启发式算法的结合也值得研究.