一类分数阶微分方程边值问题的Lyapunov不等式

武杰慧，马德香①

（华北电力大学 数理学院，北京 102206）

0 引言

1907年，Lyapunov［1］提出，对于下列边值问题：

1 相关概念及引理

定义1函数u(t)的α阶Riemann-Liouville分数阶积分定义如下：

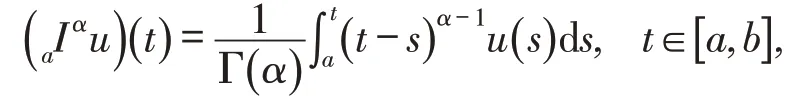
2 主要结果

定理2当δ∈(1 ,+∞)时，若式（1）有非零解u(t)，则

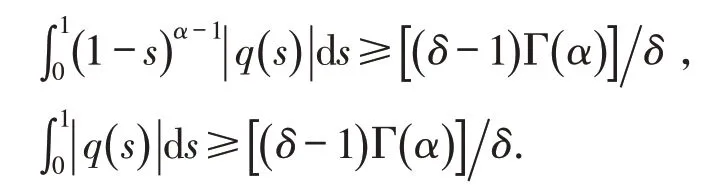
定理3当δ∈( -( α-1) ( 2-α),0)时，若式（1）有非零解u(t)，则

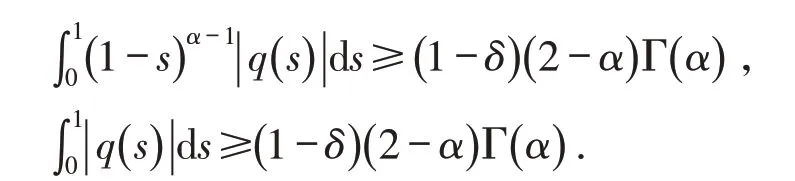
3 应用

3.1 特征值问题

讨论下列特征值问题

由定理1、定理2和定理3，易得到以下结果.

推论1（i）当δ∈( 0,1)时，对∀| λ|＜(1 -δ)Γ(α)，式（13）无非零解.

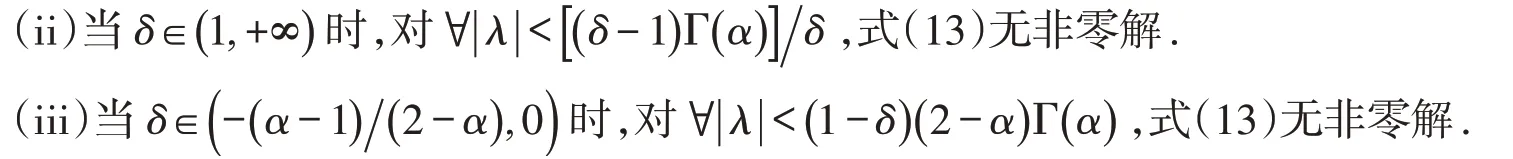
证明（i）假设u0(t)是特征值问题式（13）相对应于 |λ0|＜(1 -δ)Γ(α)的非零解，由定理1得：|λ0|≥(1 -δ)Γ(α).与假设矛盾.

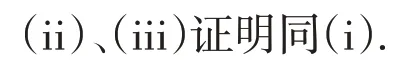
3.2 解的存在唯一性

则式（14）有唯一解.