记忆性洪灾模型及其债券定价

张节松，张 勇

（淮北师范大学 经济与管理学院，安徽 淮北 235000）

0 引言

我国大约有2/3的国土面积遭受过不同程度的洪涝灾害.洪灾的发生常常带来超几百亿元的巨额损失，单纯依靠政府的无偿赈灾与救济，不仅加重政府财政负担，也不利于灾后恢复效率的提高，迫切需要新型的风险转移方式.我国的国家突发事件应急体系建设“十三五”规划明确指出，要加快推进巨灾保险制度，推动地震巨灾保险立法进程，逐步形成多层次的巨灾风险分散机制.

当前巨灾模型探究中，通常采用传统的泊松过程刻画其发生次数［1-4］.众所周知，泊松过程是无记忆的随机过程，其指数等待时间具有马尔可夫特性［5-7］.Lin等［8］指出，以往大多数研究采用的泊松过程似乎不足以描述灾难性事件达到的过程，巨灾损失分布具有厚尾特征［9］.Saichev等［10］引入Kolmogorov-Feller等式的分数推广，并对其求解进行分析，提出分数等待时间分布函数.Mainardi等［11］指出，分数泊松过程可捕获非指数等待时间分布经验的长期记忆.Repin等［12］考虑一个具有随机强度的泊松过程，其中跳跃之间的间隔分布由具有分数导数的等式描述.Laskin［13］以Kolmogorov-Feller方程的分数推广为基础，提出一种分数非马尔可夫泊松随机过程，即分数泊松过程.Cahoy等［14］给出分数泊松过程等待时间的参数估计.Wang等［15］对复合分数阶泊松过程进行深入研究，给出复合分数阶泊松过程的参数估计.Zhang［16］则将复合分数泊松过程应用于保险实务，研究最优分层再保险问题.

受前述研究的启发，本文利用分数泊松过程拟合洪灾损失次数，捕捉洪涝灾害等待时间的长期记忆性特征，并根据风险中性定价原理，构建一个记忆性洪灾定价模型，以期更好地拟合洪灾实际，并揭示记忆性特征对债券价格的影响.

1 洪涝灾害损失次数的拟合

本文数据主要来源于中华人民共和国水利部颁布的《中国水旱灾害公报》整理所得（在线主页http：//www.mwr.gov.cn/sj/）.选取中国大陆地区从2006年1月1日至2018年12月31日洪涝灾害造成的直接经济损失为研究对象，共计89个洪涝灾害损失样本.以半年为单位，统计半年内洪涝灾害发生的次数，总共26个样本.根据洪涝灾害的原始数据，编制中国大陆地区洪涝次数的频数和频率分布表（如表1所示）和经验累计分布函数图（如图1所示）.

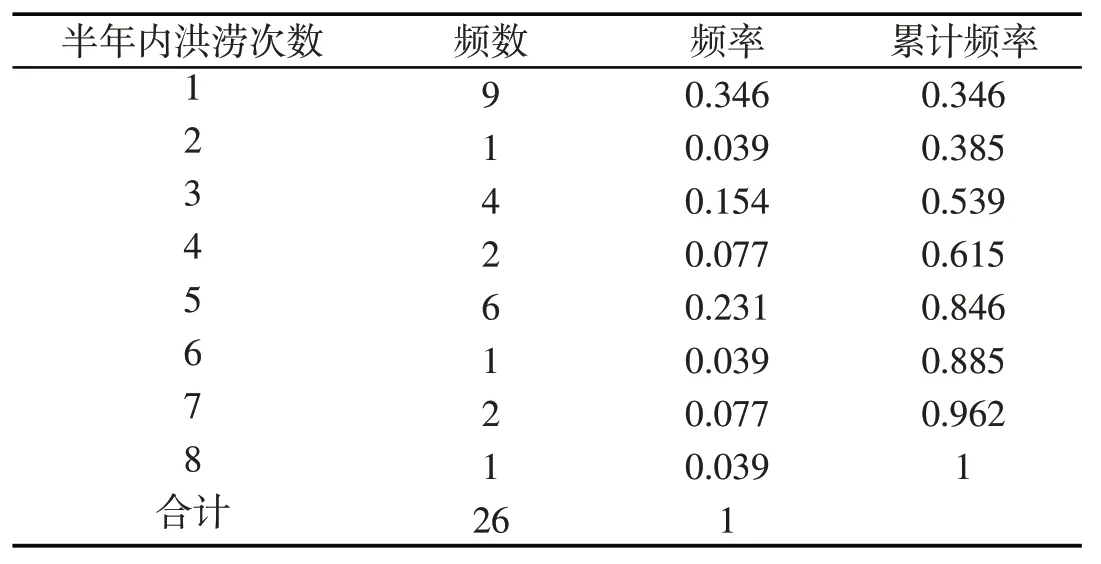
表1 洪涝次数的频数和频率分布

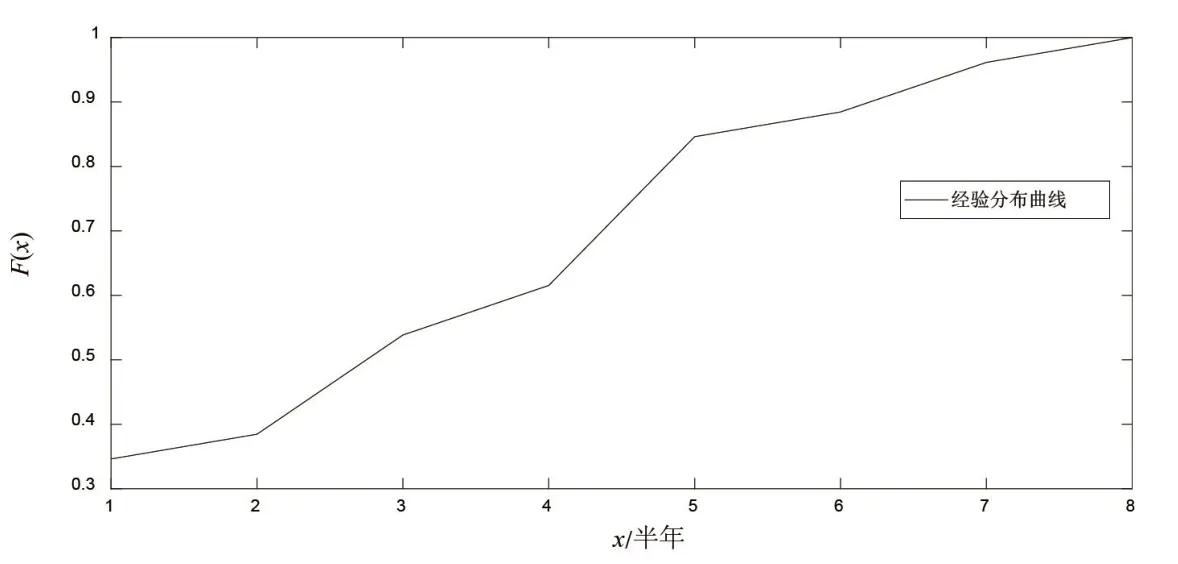
图1 洪涝灾害次数的经验累计分布函数图

1.1 洪涝灾害次数的泊松过程检验

假设H0：半年内洪涝灾害次数X服从参数为λ的泊松过程，其分布函数为：

记Xi表示半年内洪涝灾害发生的次数；fi表示实际发生洪涝灾害次数的频数，pi表示理论发生洪涝灾害次数的概率，i=1,2,…,8.

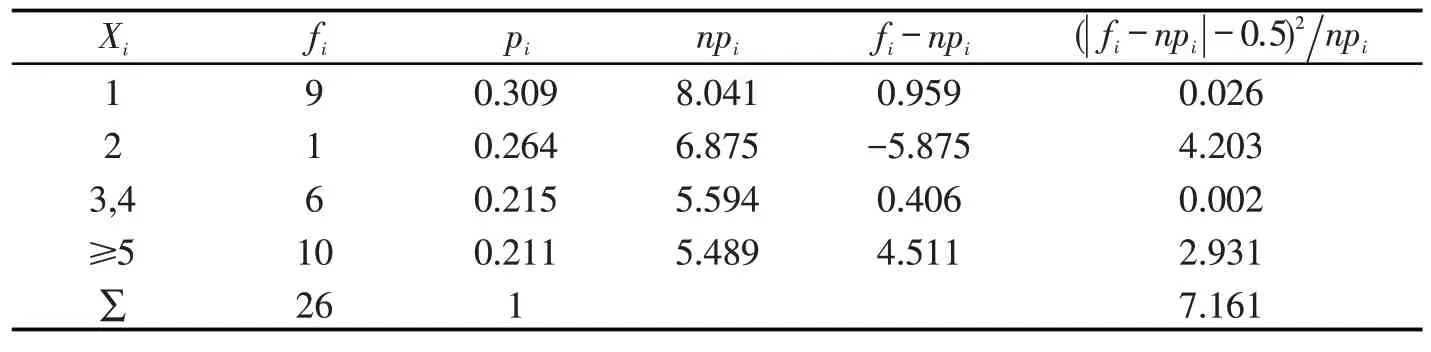
表2 样本数据校正卡方值检验

1.2 洪涝灾害次数的分数泊松过程检验

假设H′0:半年内洪涝灾害次数Nv(t)是服从参数为v的Mittag-Leffler型分数泊松过程，其分布函数为:

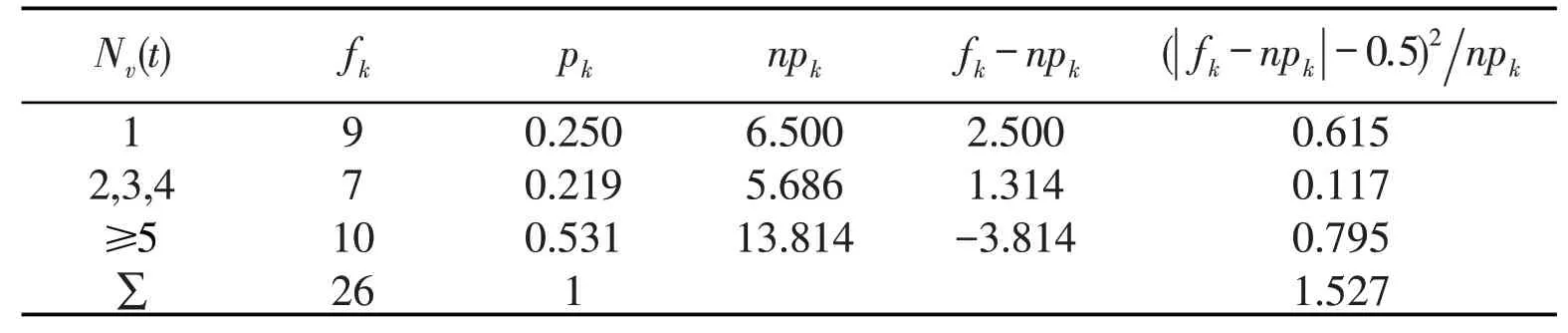
表3 样本数据校正卡方值检验

1.3 拟合效果比较及模型的确定

进一步，借鉴Lin等［8］4个拟合全局度量的方法，比较泊松过程和分数泊松过程，计算结果如表4所示.

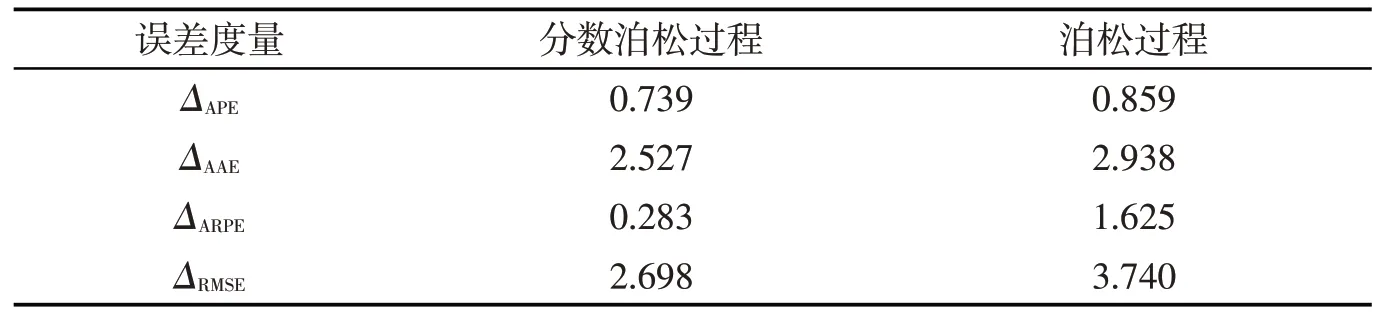
表4 全局拟合误差度量

其中，ΔAPE、ΔAAE、ΔARPE和ΔRMSE分别是对平均百分位误差（APE）、平均绝对误差（AAE）、平均相对百分位误差（ARPE）和相对均值平方误差（RMSE）的度量，计算公式为：

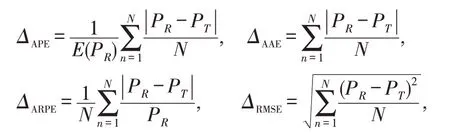
PR表示洪涝次数的实际频数，PT是洪涝次数的理论频数.

由表4可知，分数泊松过程的4个拟合全局度量值均小于泊松过程，这就意味着分数泊松过程比泊松过程更适合洪涝灾害债券定价时的洪涝次数的拟合.因此，选取分数泊松过程作为中国大陆地区洪涝损失过程.中国大陆地区洪涝灾害发生的次数服从下列分数泊松过程：

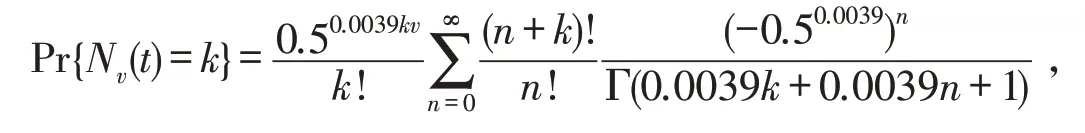
其中Γ(x)为伽马函数.

2 洪涝灾害债券定价

瑞士再保险研究院发布的《经济积累和气候变化时期的自然灾害》报告显示，2019年保险业的赔付中，全球保险业赔付自然灾害和人为灾害造成1 460亿美元经济损失的40%左右.而目前，中国保险业在自然灾害中的赔付比例仅为10%左右.由此可见，我国保险市场迫切需要更加有效风险转移的方式.

保险连接债券连通保险市场和资本市场，借用资本市场分散保险市场的风险.此外，巨灾风险债券具有无信用风险和增加保险公司承保能力的优点.发行巨灾债券的关键是科学的定价，因此更贴合实际的风险模型为合理定价提供理论基础.下面对记性洪灾模型进行定价，并与无记忆性进行比较.

2.1 记忆性洪灾定价模型的建立

记忆性洪灾债券价格的定价模型是采用考虑记忆参数v的Mittag-Leffler分布拟合巨灾的等待时间分布，其代替传统巨灾债券定价模型中的指数分布.此外，记忆性洪灾定价模型通过复合分数泊松过程来刻画洪涝灾害的抵达过程，并能捕捉其发生时间间隔的记忆性特征.本文根据风险中性定价原理，证券在时间内的价格等于到期损益在唯一等值鞅测度下的期望折现值［18］.借鉴Vaugirard［19］使用的计算到期损益的方法.面值为F和期限为T的零息票债券在时刻t的价格为：

2.2 洪涝灾害债券价格确定

为获得不同期限的记忆性洪灾债券价格，需要进行参数赋值.将本金损失比例w=1,0.5,0，一年期T=1、两年期T=2和三年期T=3，面值F=100，Mittag-Leffler分布的参数v=0.133，无风险利率r=2%,记忆性洪灾债券数据分别代入式（4）、式（5）和式（6）中进行定价，如图2所示.

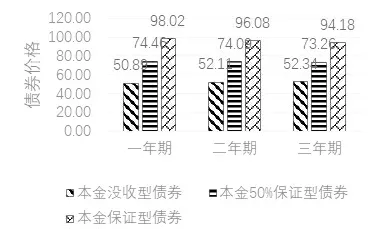
图2 不同期限记忆性洪灾债券价格

由图2可知，记忆性洪灾债券的本金损失比例越低，债券价格越高.随着债券期限越长，本金没收型债券的价格越高，因为三年期债券风险更大一些.但是本金50%保证型债券和本金保证型债券随着期限增加而降低.这些是符合市场运行规律.

2.3 洪涝灾害债券价格比较

本文将洪涝灾害发生时间分别代入服从指数分布和Mittag-Leffler分布进行债券定价，假设债券面值F=100，无风险利率r=2%，本金损失比例选取w=0.5和w=1，得到无记忆性洪灾债券和记忆性洪灾债券价格，如表5所示.由表5可以看出，传统采用指数分布进行的无记忆性债券定价价格较高，且不受本金损失比例变化的影响.与传统的无记忆性债券相比，记忆性洪灾债券价格随着本金损失比例的增加而降低，且期限越长债券价格有所下降.

表5 记忆性和无记忆性洪灾债券价格表

3 结语

我国是洪涝灾害频发的发展中国家，能否补偿洪涝灾害所造成的损失对社会经济发展有很重要的作用.在分散巨灾风险和补偿巨灾损失方面，巨灾保险证券化起着独特的优势.因此，通过发行更加合理的洪涝灾害债券符合当前发展的迫切需要.

本文通过对洪涝灾害损失次数进行卡方检验和4个全局度量的比较，得出采用分数泊松过程模拟洪涝灾害的次数分布更优，并利用Mittag-Leffler分布拟合洪涝灾害的等待时间，利用风险中性定价原理给出记忆性洪灾债券的价格.考虑非指数等待时间分布的分数泊松过程更好地拟合次数分布，这为准确地评估洪涝债券定价提供一定基础.通过对比传统的无记忆性洪灾债券定价，发现记忆性洪灾债券定价更加合理.本文仅对洪涝灾害债券做初步设计，关于其他类型的巨灾债券定价还需要进一步的研究.