一种抑制盘式永磁电机转矩脉动的方法

江 爽，于慎波，于言明，夏鹏澎，窦汝桐，翟凤晨

(1.沈阳工业大学 机械工程学院，沈阳 110870；2．中国邮政集团公司 辽宁省机要通信局，沈阳 110870)

0 引 言

盘式永磁电机具有高转矩惯量比，结构紧凑，效率高，功率密度大等优点。但其由于采用均匀气隙的结构，导致气隙磁密波形和反电势波形中含有大量的谐波，转矩脉动较大，降低电机运行的平稳性，产生振动噪声。因此，合理设计盘式永磁电机磁极形状，有利于改善气隙磁密波形和反电势波形，抑制转矩脉动，提高电机性能。

在盘式永磁电机设计的初级阶段，可以建立该电机简化磁网络模型，基于此模型可以求出电机的空载反电势。文献[1，2]通过建立轴向磁场永磁电机的简化磁网络模型，得到了电机的空载反电势及负载电磁转矩，并且经过了实验的验证，相比于有限元法节约了大量的时间。文献[3]系统的介绍了永磁同步电机转子的优化技术，针对表贴式永磁同步电机，可以采用组合磁极，磁极偏心，正弦削极，谐波削极等的方式削弱气隙磁密和反电势的谐波含量。文献[4]提出了正弦弧永磁体的设计方法，通过实验验证表明该方法能有效改善反电势波形，降低相电势的谐波。文献[5]针对永磁电机弓形磁极，建立了简化正弦削极、修正正弦削极、简化三次谐波削极、修正三次谐波削极模型，结果表明在平行充磁条件下，修正三次谐波削极在降低电机转矩脉动和提高电机转矩密度2个方面都有显著的效果。文献[6]分析了一台6槽4极的电机采用正弦削极的方式下的不同永磁体边缘厚度时的空载反电势波形，结果表明永磁体边缘厚度为0时，反电势波形符合正弦波。文献[7]分析了一台12槽10极电机采用正弦削极的方式下的不同永磁体边缘厚度时的气隙磁密波形，结果表明永磁体边缘厚度为1mm时，气隙磁密谐波含量最小。同时在正弦削极的永磁体中注入3次谐波来增大气隙磁密的基波幅值，提高电机的输出转矩。同时发现，采用正弦削极和在正弦削极的永磁体中注入3次谐波这两种优化方式都能有效地抑制转矩脉动。文献[8]提出一种由导磁金属块和永磁体共同构成的表贴式磁极结构，在矩形永磁体表面上覆盖一个偏心圆弧形的导磁金属块，从而实现不均匀气隙结构，有效改善了气隙磁密波形的正弦度，削弱了反电势中的谐波含量，提高了电机的效率和运行平稳性。

本文建立了盘式永磁电机简化磁网络模型，基于此模型求解出电机的空载反电势，并用有限元法进行了验证。基于正弦削极的优化技术，提出一种针对扇形永磁体采用的圆弧削极的优化技术。为提高削极后的平均转矩，采用偏心圆弧削极的方式来等效传统的在正弦削极的永磁体中注入3次谐波的优化磁极方式。通过对比不同优化方式的气隙磁密，平均转矩，转矩脉动等电磁性能，得到了最佳优化方案。

1 盘式永磁电机空载反电势的计算

1.1 简化磁网络模型的建立

轴向磁场盘式永磁电机结构示意图如图1所示。电机模型参数如表1所示。该电机额定功率为5 kW，额定转速为450 r/min。

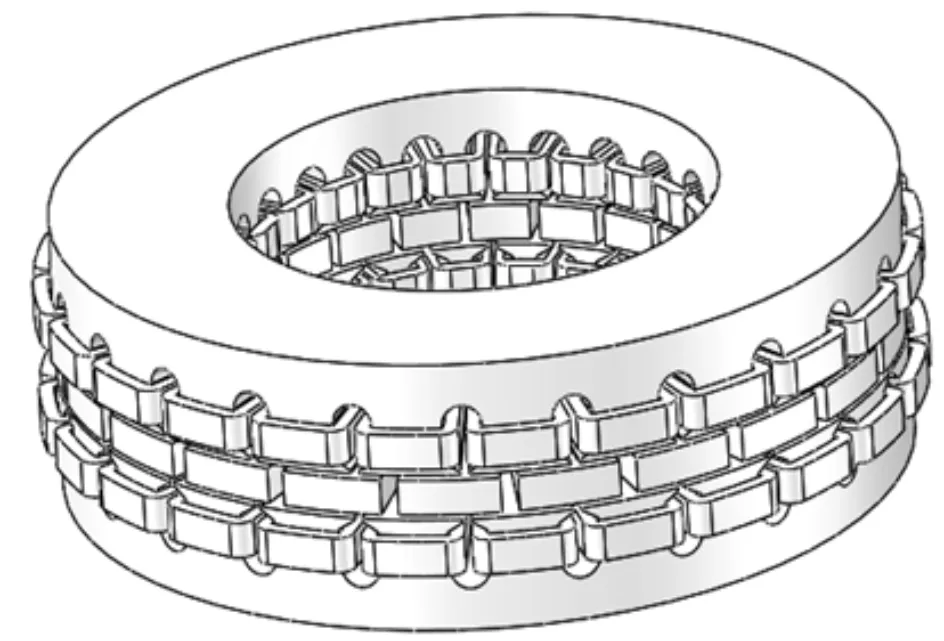
图1 盘式永磁电机结构示意

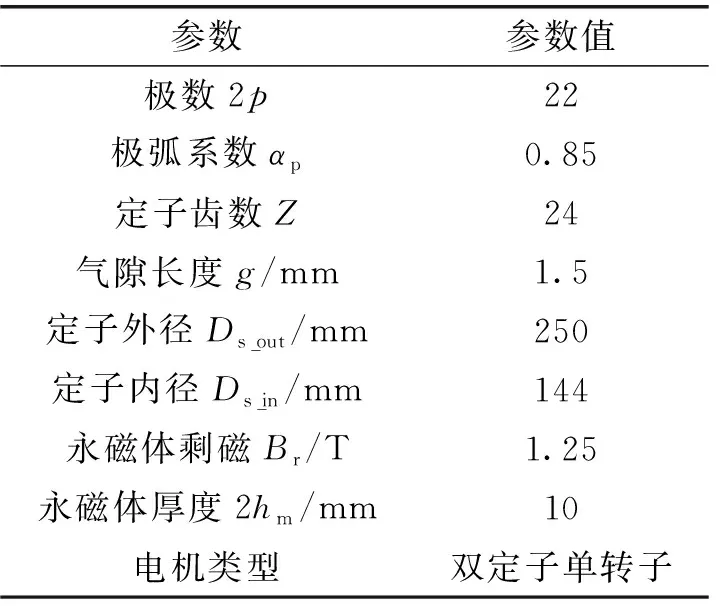
表1 盘式永磁电机参数

盘式永磁电机沿永磁体平均半径处的平面展开图如图2所示，其中，A、B、C代表电机绕组的分相，“+”、“-”代表组成绕组的线圈内电流的方向。由于盘式永磁电机具有良好的对称性，因此只需取一个极距范围进行分析。图3为一个极距范围盘式永磁电机的等效磁网络模型。考虑到磁路的对称性，可以将图3简化为图4。其中，Φr为永磁体虚拟内禀磁通,Φm为永磁体向外磁路提供的总磁通，Φg为气隙主磁通，Rg为气隙磁阻，Rm为永磁体自身磁阻，Rmo为永磁体外周边缘漏磁，Rmi为永磁体内周边缘漏磁磁阻，Rmr为永磁体沿圆周方向漏磁磁阻，Rmm为相邻永磁体之间漏磁磁阻，Rc为电枢电阻，Fad为电枢反应产生的电动势。

图2 盘式永磁电机平面展开图

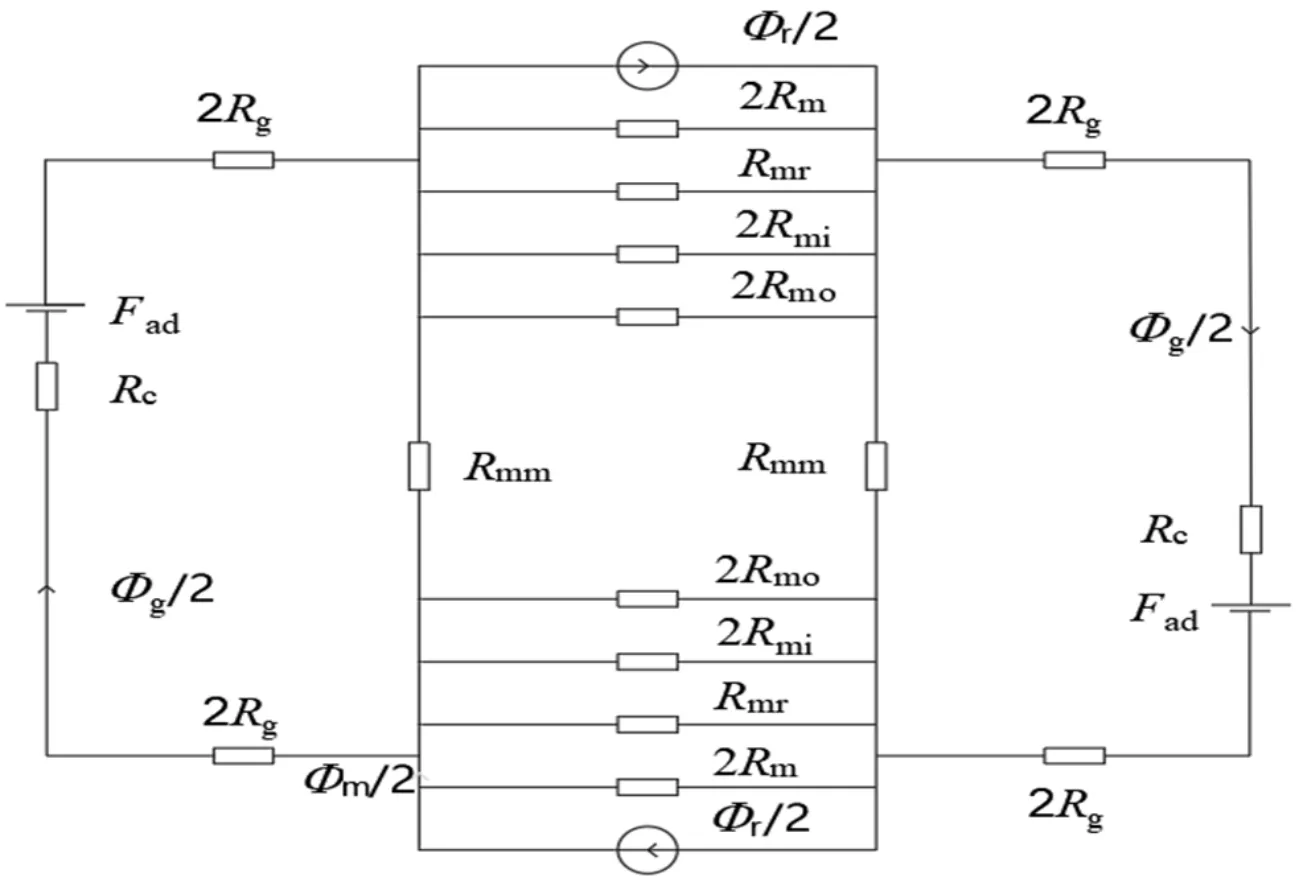
图3 盘式永磁电机等效磁路磁网络

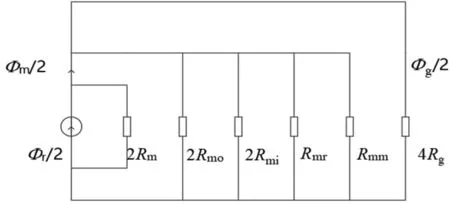
图4 盘式永磁电机简化磁网络

根据图4所示简化磁网络模型，可以得到单个齿上的磁通最大值为

(1)

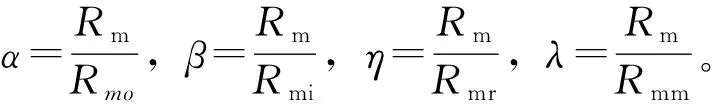
各部分磁阻可以表示为

(2)

式中，hm为永磁体厚度，μ0为真空磁导率，μr为永磁体相对磁导率，αp为极弧系数，p为极对数，Dmo为永磁体外直径，Dmi为永磁体内直径，L1、L2为永磁体内、外周边缘轴向长度，L3为永磁体内外半径之差，bm为永磁体极间距离,g为气隙长度。

1.2 反电动势的计算

该电机为22极24槽结构，且电机具有半周期对称性，因此只需分析1个基本单元内每相绕组内两个定子齿中的磁通变化情况。A相绕组第一个定子齿A1和第二个定子齿A2上的磁通可以表示为

(3)

A相绕组磁链可以表示为

(4)

由磁链表达式可以求出电机A相绕组反电势为

(5)

式中，θ为电机旋转角度，ω为电机旋转的角速度，Nc为线圈匝数。B、C两相绕组的反电势分别落后A相绕组反电势2π/3和4π/3。

在一个极距范围内A相绕组反电势解析法与有限元仿真得出的对比图如图5所示，解析计算出A相绕组反电势的有效值为45.63 V，有限元仿真出-A相绕组反电势的有效值为45.27 V，误差为0.79%。

图5 A相绕组反电动势对比图

2 磁极结构的有限元分析

2.1 圆弧削极优化方案

盘式永磁电机沿永磁体平均半径处的气隙磁密如图6所示，从图中可以看出气隙磁密波形的正弦性不是很好，因此需要对其进行优化。目前较为普遍的方式是采用正弦削极，但此种削极技术大多针对的是弓形永磁体。针对盘式永磁电机采用的扇形永磁体，本文提出一种圆弧削极的技术，其解析模型如图7所示。理论思想：通过圆弧削极来等效正弦削极，构成不均匀气隙结构。比较不同削极圆弧半径下的气隙磁密波形畸变率，选择畸变率最低的方案，即为最接近正弦削极的优化方案，以此达到优化气隙磁密波形的目的。

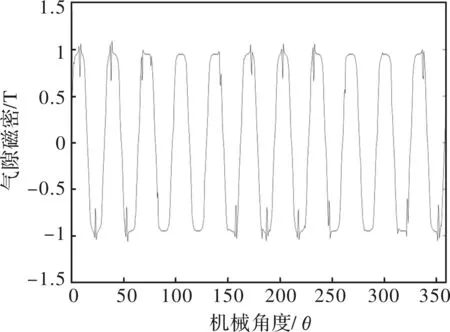
图6 盘式永磁电机平均半径处气隙磁密

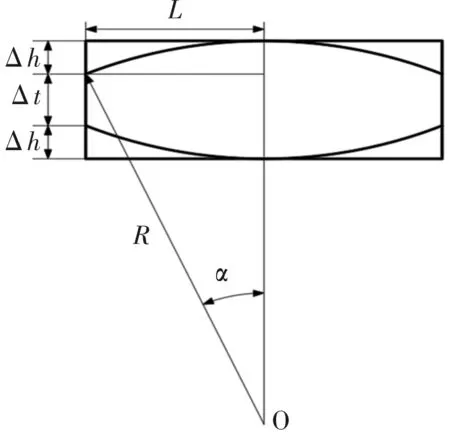
图7 圆弧削极解析模型

由图7可得参数方程：

(6)

由式(6)可得

(7)

式中，Δt为削极后永磁体的端部厚度，R为削极圆弧的半径长，2L为永磁体的周向长度。

通过有限元仿真分析得出削极后不同永磁体端部厚度下的气隙磁密谐波分析对比图。图8为采用不同半径圆弧切削永磁体后的气隙磁密谐波对比图。图9比较了削极后不同永磁体端部厚度下气隙磁密波形正弦畸变率的变化情况。

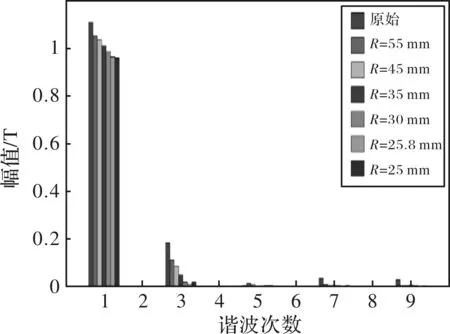
图8 不同半径圆弧削极下的气隙磁密谐波对比

综合图8和图9可以看出随着切削圆弧半径的减小，永磁体端部厚度的减小，气隙磁密波形的畸变率逐渐变小。当切削圆弧半径为25.8 mm，即永磁体端部厚度为0时，气隙磁密波形的畸变率最小。此时，气隙磁密波形的畸变率由原来16.99%下降到优化后1.10%。

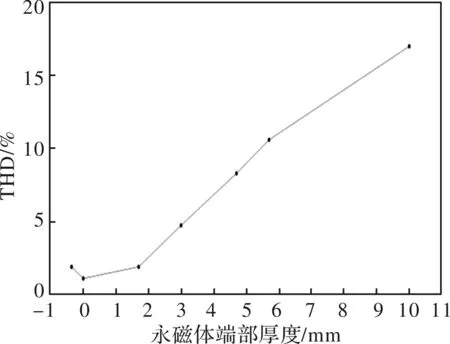
图9 气隙磁密THD与永磁体端部厚度的关系

2.2 偏心圆弧削极优化方案

采用削极的优化方式会降低电机的平均输出转矩，传统的解决方法是通过在正弦削极的永磁体中注入3次谐波增大气隙磁密基波幅值，来提高电机输出转矩。本文采用偏心圆弧削极的方式来等效传统的优化方式，其解析模型如图10所示。理论思想：通过采用两个偏心圆弧削极的方式，模拟传统方式永磁体外表面曲线结构，比较不同偏心距和圆弧半径组合削极方式下的气隙磁密基波幅值和气隙磁密波形畸变率，选择幅值最大、畸变率最小的一组方案，以此达到提高气隙磁密基波幅值和平均输出转矩的目的。

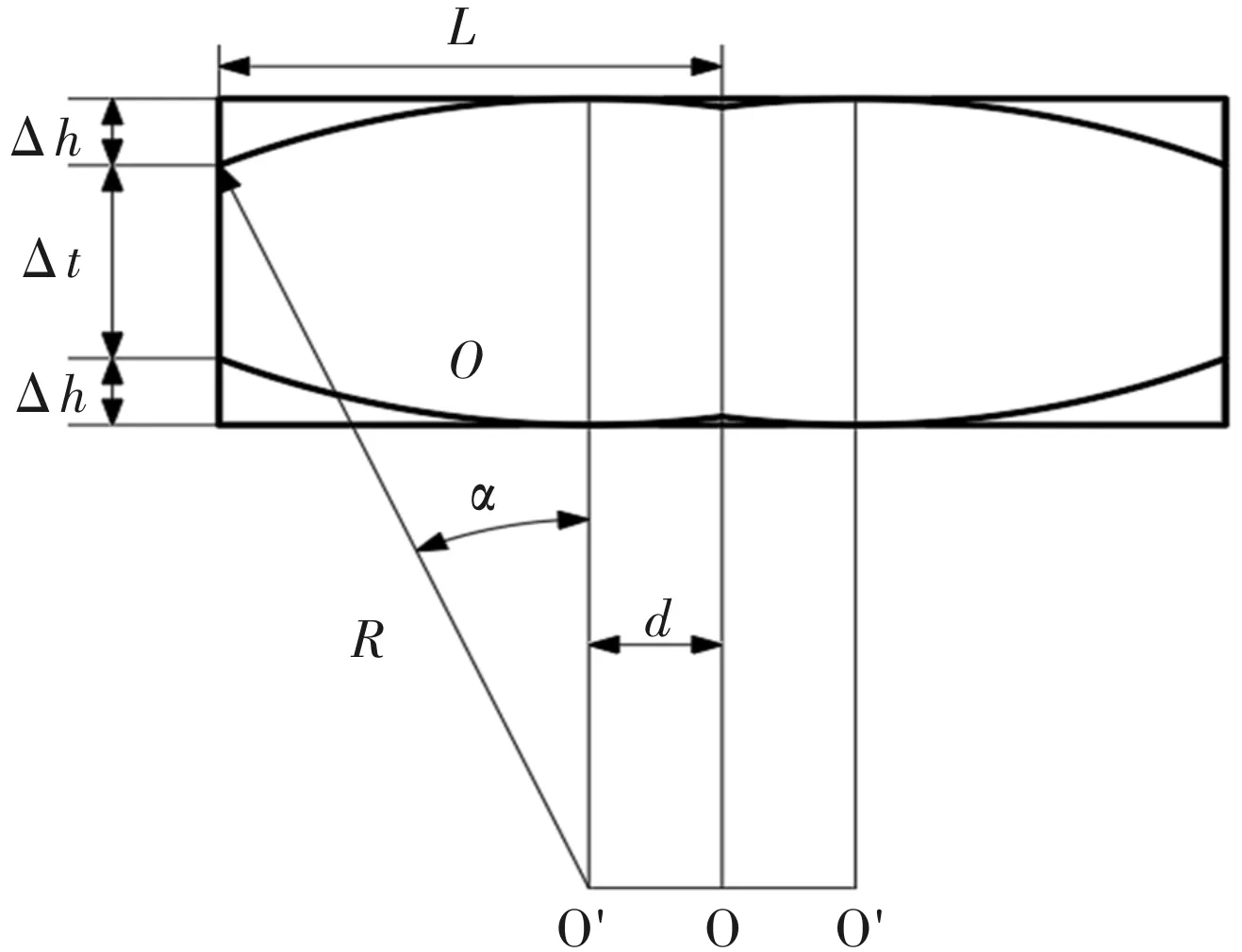
图10 偏心圆弧削极解析模型

由图10可得参数方程：

(8)

由式(8)可得

(9)

式中,d为偏心距。

通过有限元仿真分析得出削极后不同永磁体端部厚度下的气隙磁密谐波分析对比图。图11为采用不同半径和偏心距圆弧切削永磁体后的气隙磁密谐波对比图。表2列出了削极后不同永磁体端部厚度下气隙磁密波形的畸变率。

图11 不同半径和偏心距圆弧削极下的气隙磁密谐波对比

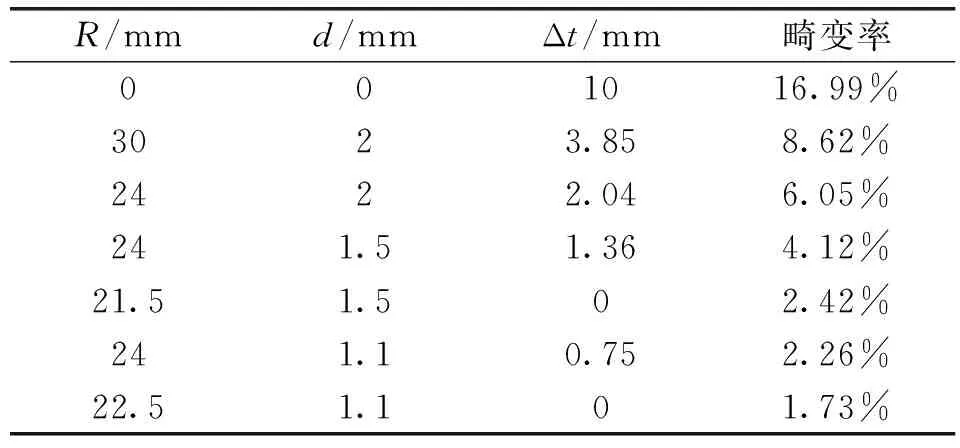
表2 不同永磁体端部厚度下气隙磁密波形的畸变率

综合图11和表2可以看出，采用偏心圆弧削极后，气隙磁密基波幅值提高；随着偏心距与切削圆弧半径的减小，气隙磁密波形的畸变率逐渐减小，但偏心距过小会导致气隙磁密基波幅值大幅下降，因此选择最佳优化方式是偏心距为1.1 mm,半径为22.5 mm的圆弧削极。此时，气隙磁密波形的畸变率由原来的16.99%下降到优化后的1.73%。

考虑到采用偏心圆弧削极这种优化方式时，永磁体上下部分的凹槽较难加工，因此采用一种改进的偏心圆弧削极优化方式，即保持凹槽部分的气隙为均匀气隙(最小气隙长度)。改进后的磁极模型如图12所示。

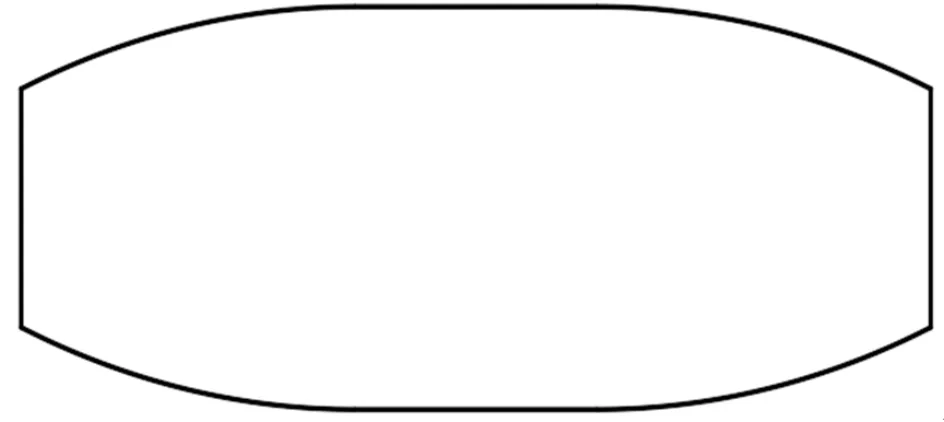
图12 改进后磁极模型

2.3 三种优化方案电磁性能的对比

图13为三种优化方案的气隙磁密谐波对比图。图14为三种优化方案的输出转矩对比图。

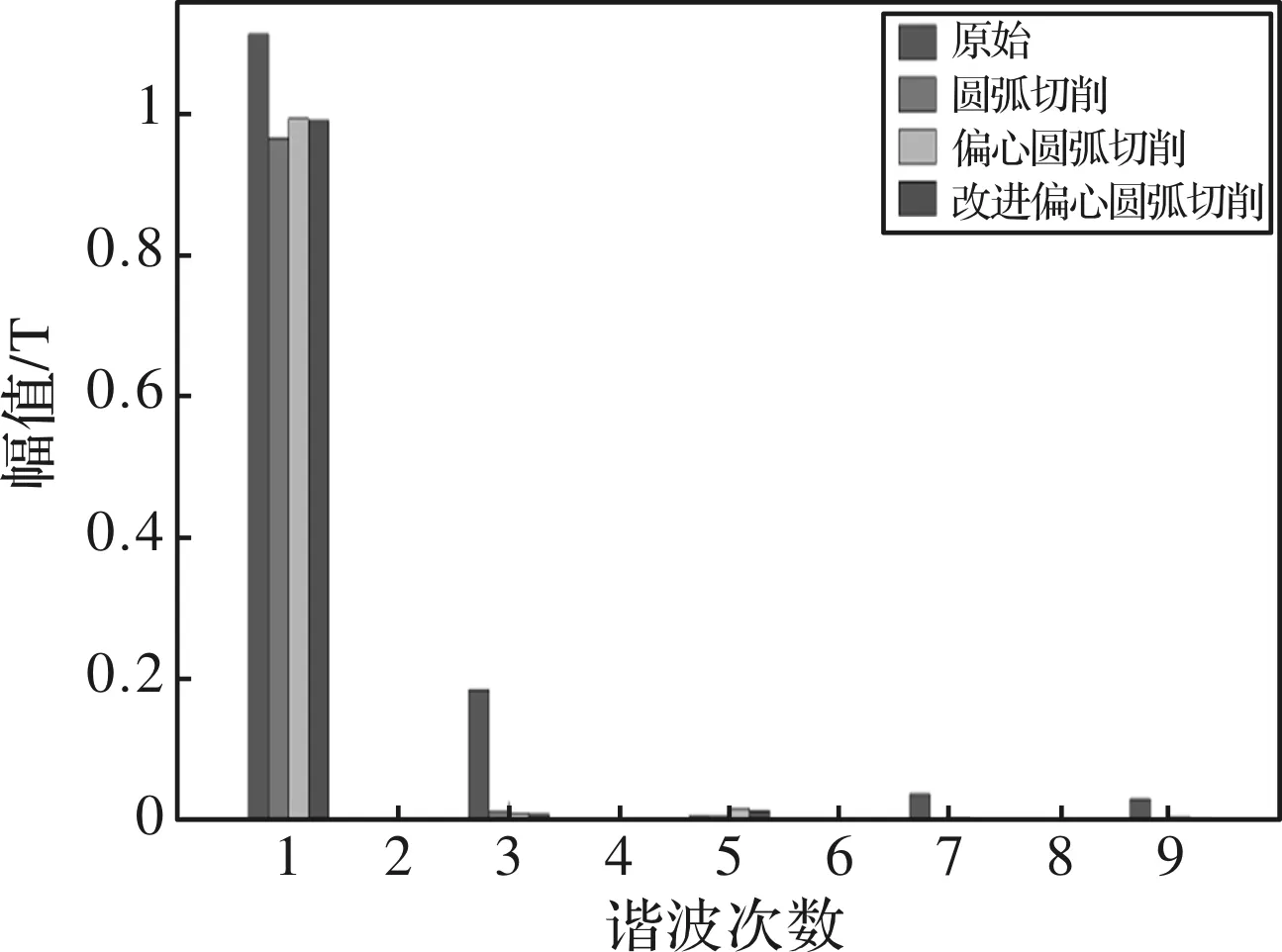
图13 气隙磁密谐波对比

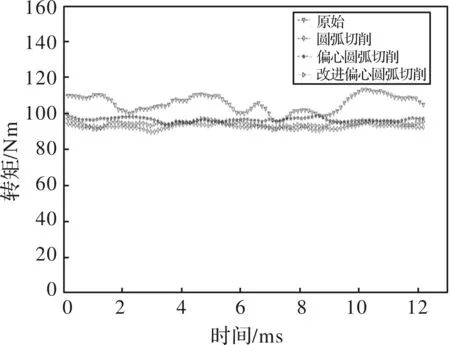
图14 输出转矩对比

转矩脉动的表达式为

(10)

式中，Tmax、Tmin分别为最大、最小转矩。kt越小，说明转矩脉动的抑制效果越好。表3列出了三种优化方案的转矩脉动对比。表中Tav为平均转矩。图15为三种优化方案的反电势谐波对比图。他们的反电势波形的畸变率依次为6.52%、1.18%、0.88%、2.59%。

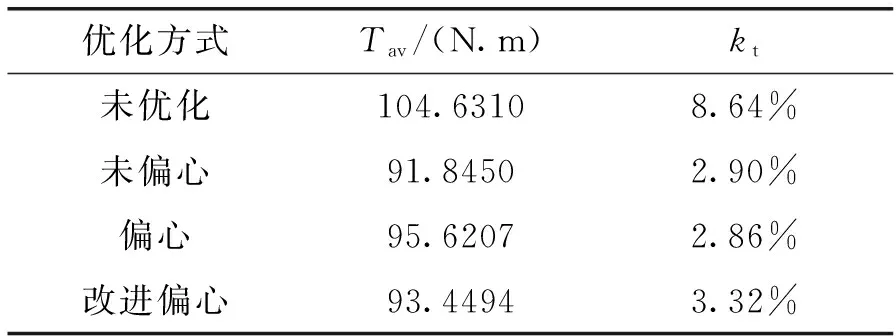
表3 转矩脉动对比

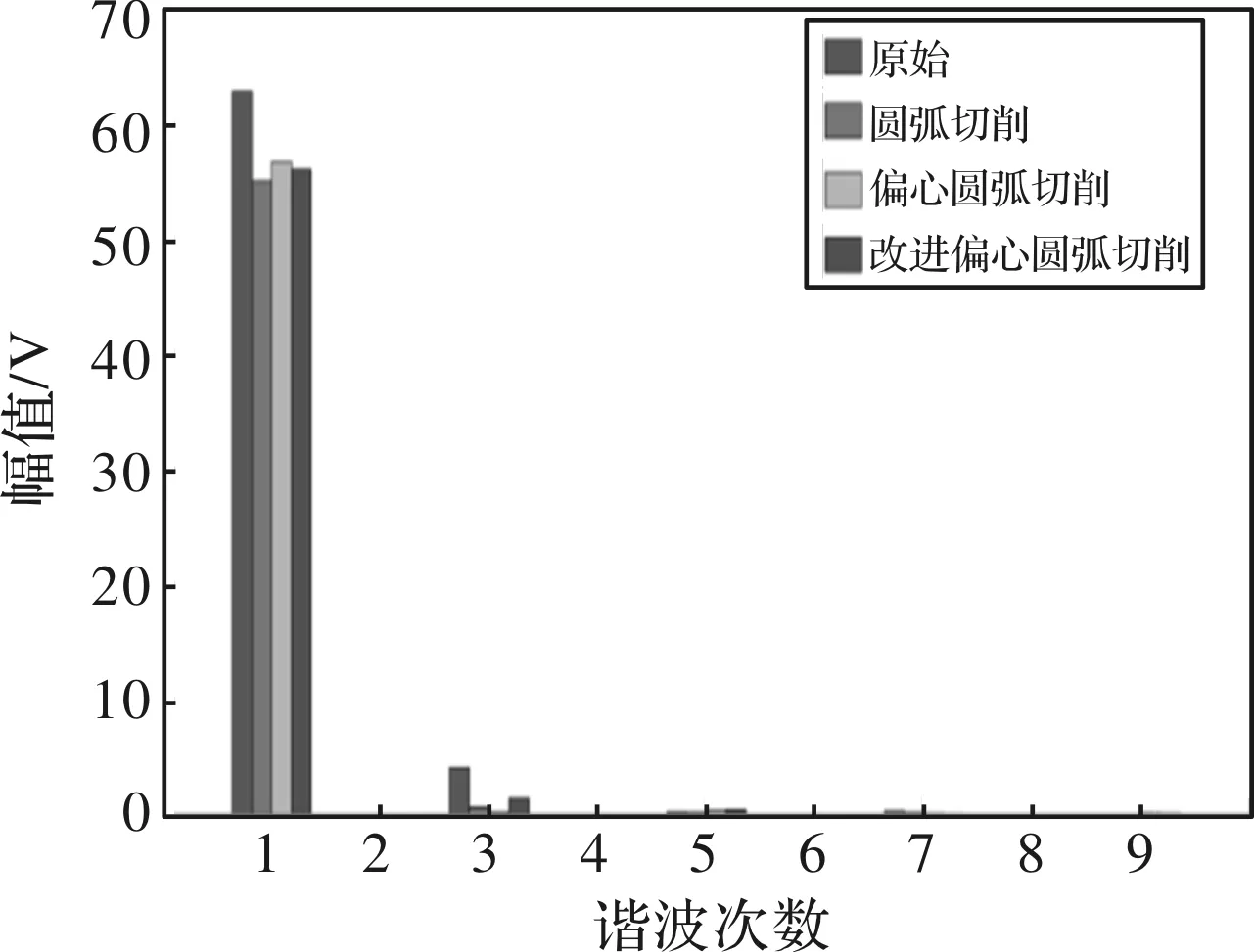
图15 反电势谐波对比

通过以上对比，可以得出结论：最佳优化方式是偏心距为1.1 mm,半径为22.5 mm的圆弧削极。

3 结 论

本文基于等效磁网络法建立了盘式永磁电机磁场解析模型，对电机磁极进行了优化，并针对一台22极24槽双定子单转子盘式电机电磁设计方案进行了分析，结果显示：

(1)解析法与有限元法计算反电势有效值误差为0.79%。

(2)针对扇形永磁体，采用圆弧削极能够降低气隙磁密和反电势波形的畸变率，还能够抑制转矩脉动。削极圆弧半径越小，永磁体的端部厚度越小，气隙磁密波形的畸变率越小，当永磁体端部厚度为0时，优化情况最好。

(3)为提高圆弧削极后电机的平均转矩，采用偏心圆弧削极的优化方式来等效传统的往正弦削极的永磁体中注入3次谐波的优化方式。结果表明，与圆弧削极相比，采用偏心圆弧削极的优化方式，气隙磁密基波幅值增大、平均转矩增大、转矩脉动更小、反电势波形的畸变率更小。