考虑定子饱和的航空高速永磁电机转子涡流损耗解析模型

李 剑，江晓波，孙 鲁

(1.贵州航天林泉电机有限公司(国家精密微特电机工程技术研究中心)，贵阳 550008；2.空装成都局驻贵阳地区第一军代表室，贵阳 550008)

0 引 言

高速永磁同步电机由于其高效高功率密度的特点，在航空航天领域有着广泛的应用[1-2]。但由于高速电机体积小的特点，电机转子的散热条件差。在变频启动时，高次电流时间谐波会在转子上产生大量的涡流损耗，使永磁体温升过高，增大永磁体的不可逆失磁风险[3-4]。随着航空武器装备性能不断提高，对电机体积和电磁极限设计提出更高的要求。在定子齿轭磁密饱和时会影响磁导谐波变化，进而影响转子的涡流损耗的计算精度。因此构建考虑定子饱和的转子涡流损耗解析模型是必要的。

目前对转子涡流损耗的研究已经是高速永磁电机研究的一个重要方向。文献[5-8]从定转子结构机进行优化，通过有限元的方法对不同绕组形式、护套材料分析，有效的抑制转子的涡流损耗。有限元方法计算转子涡流损耗可以考虑各种复杂结构，材料非线性等因素。但由于需要对模型进行精细化剖分，计算时间较长，不利于电机方案的设计和调整。

采用解析的方法可以有效的解决损耗计算时间长的问题，并可以从理论上对转子涡流损耗进行研究。等效电阻网络法分析不同电机结构的转矩和损耗性能。但模型通用性较差，在结构发生变化时，需要重新搭建模型[9-10]。子域法通过对电机分域并建立拉普拉斯方程，计算速度快[11-14]。但子域法在建模时假设定转子磁导率无穷大，忽略了在极限设计时定子饱和的影响，造成误差。

采用实验的方法对高速永磁同步电机转子涡流损耗进行直接测量极为困难。文献[15]采用损耗分离的方法分别对铜耗，机械损耗，定子铁心损耗进行实验，最终分离出转子的涡流损耗。

本文将子域法和等效磁路法相结合，通过把电流片和磁通带入两个模型中迭代计算，建立考虑定子齿轭以及齿尖饱和的转子涡流损耗解析模型。为提高模型的计算精度，通过磁导模型考虑了定子开槽的影响。基于该解析模型分析不同气隙长度和槽口宽度对转子涡流损耗的影响。最后通过损耗分离实验对转子涡流损耗进行损耗分离，将解析结果和有限元以及实验结果对比，验证解析模型的正确性。

1 考虑定子饱和的转子涡流损耗模型

1.1 解析模型建立

针对航空高速永磁同步电机的转子涡流损耗建立考虑定子饱和的转子涡流损耗解析模型。如图1所示，通过将定子的饱和效应等效为分布在定子内径处的等效电流片，得到定子饱和对转子涡流损耗的影响。

对解析模型做出必要的假设：

(1)永磁体和护套材料各向同性，电导率和磁导率为常数，磁导率分别为μpm，μs1电导率为σpm，σs1。

(2)电枢绕组等效为均匀分布在槽口的等效电流片。

(3)忽略涡流端部效应的影响。

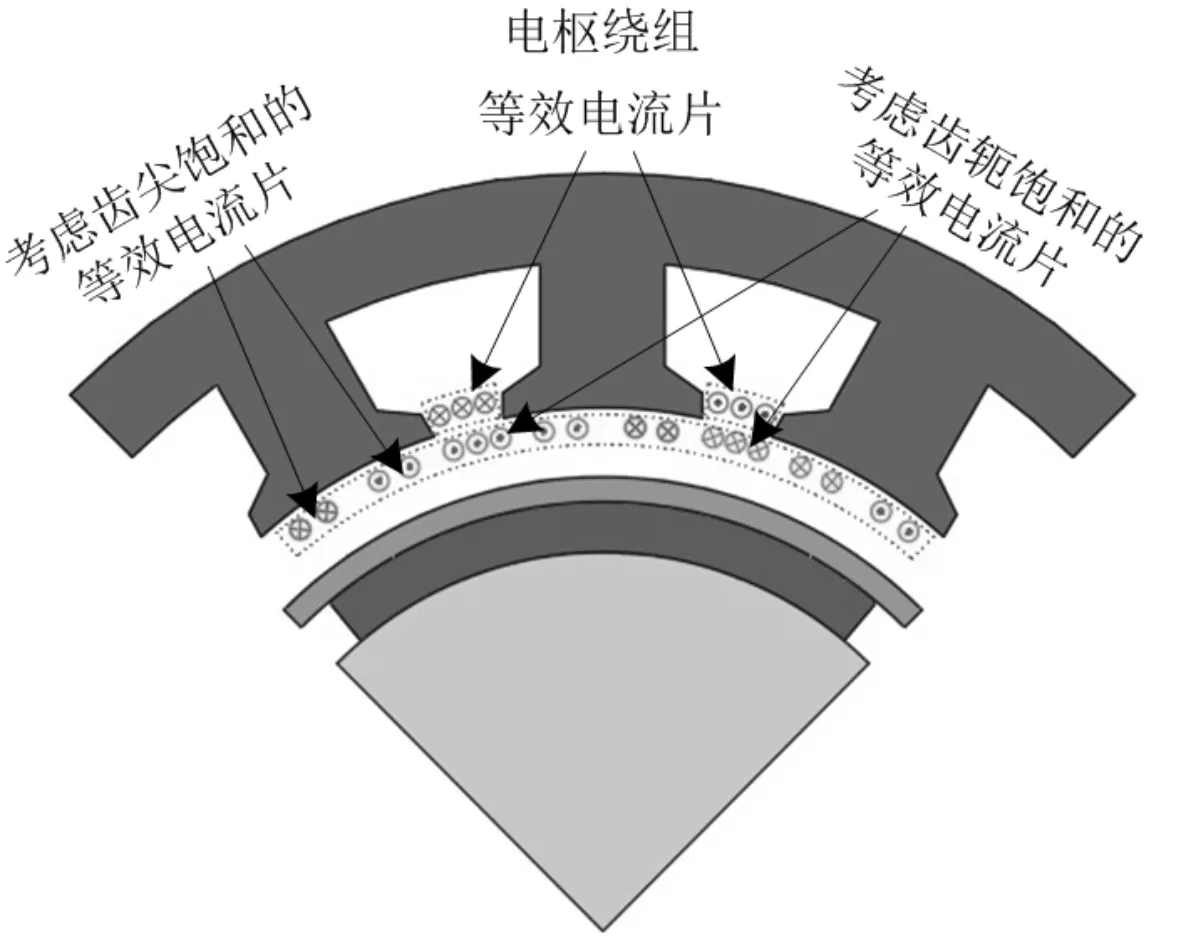
图1 考虑定子饱和的转子涡流损耗解析模型

1.2 不考虑定子饱和的转子涡流损耗模型

根据图1(a)解析模型，将电枢绕组等效为等效电流片[18]，三相合成电流密度为

(1)

其中，m，n分别为电流谐波次数和磁场空间谐波次数，ωr为转子的角速度，α为旋转坐标系下的周向角度。θ为静止坐标下的周向角度。N为每槽导体数，In为各次时间谐波的幅值，ksov为绕组的槽口系数，kdp为绕组系数。Rs为定子内径。

分别对气隙子域，护套子域和永磁体子域列写拉普拉斯方程，为了考虑涡流反作用的影响，对护套和永磁体建立扩散方程[3]：

(2)

其中，AI为气隙中的矢量磁位，JZII为护套上产生的轴向涡流密度，JZIII为永磁体上产生的轴向涡流密度。

则电枢磁场在气隙中产生的磁密分布为

(3)

其中，BrI，HαΙ分别气隙磁密的径向分布和磁场强度的切向分布，A，B分别为与气隙子域边界条件相关的系数

护套和永磁体中的磁场强度为

(4)

其中，C，D，E，F分别为与护套和永磁体子域边界条件相关的系数。

在不考虑定转子饱和时，各子域之间的边界条件为

(5)

永磁体和护套的总损耗分别为

(6)

1.3 定子饱和对转子涡流损耗的影响

根据航空电机电磁性能极限设计的特点，定子齿轭会产生局部饱和的现象，影响磁导谐波变化，进而影响转子涡流损耗。采用等效磁路的方法，在分别对定子齿轭以及齿尖搭建磁路，对各支路磁导进行迭代计算。磁路模型如图2所示。

图2 定子饱和等效磁路图

图2为对一对定子齿搭建的等效磁路，将定子的饱和效应等效为均匀分布在定子内径处的等效电流片，按照图2所示的磁路对整个电机进行磁路搭建。其中Φs为气隙中的磁通，由等效电流片产生的磁场和永磁体在气隙中产生的磁场两部分组成。永磁体产生的磁密为[16]

(7)

其中，C1,C2为与永磁体参数相关的量，n1为永磁体产生磁场空间谐波次数，p为极对数，Mn，Mn1分别为永磁体磁化强度和永磁体磁化强度径向分量。

对等效磁路基于基尔霍夫定律列写节点电压方程[16]。

(8)

其中，A1为关联矩阵，Λ为磁导矩阵，V为结点电压矩阵，Φ为节点磁通矩阵。

将定子的饱和作用转换为均匀分布在定子内径处的等效电流Isk。通过对矩阵进行迭代计算，在矩阵收敛之后，根据等效磁路各个节点的磁动势得到定子内径处的等效电流[17]

Isk=-(Vk+2-Vk)

(9)

其中k为节点的个数。

通过傅里叶级数对等效电流片进行展开，则考虑定子饱和所等效的电流密度为

(10)

其中，v为傅里叶级数的阶数，l为气隙磁密所包含的谐波次数，b0为槽口宽度，Qs为定子槽数。

将考虑定子饱和的等效电流片带入到公式(2)中，进而得到考虑定子饱和时的转子涡流损耗。

2 转子涡流损耗解析结果

2.1 转子涡流损耗验证

以一台40 kW，36000 r/min的航空高速永磁电机为例进行解析分析，电机参数如表1所示。

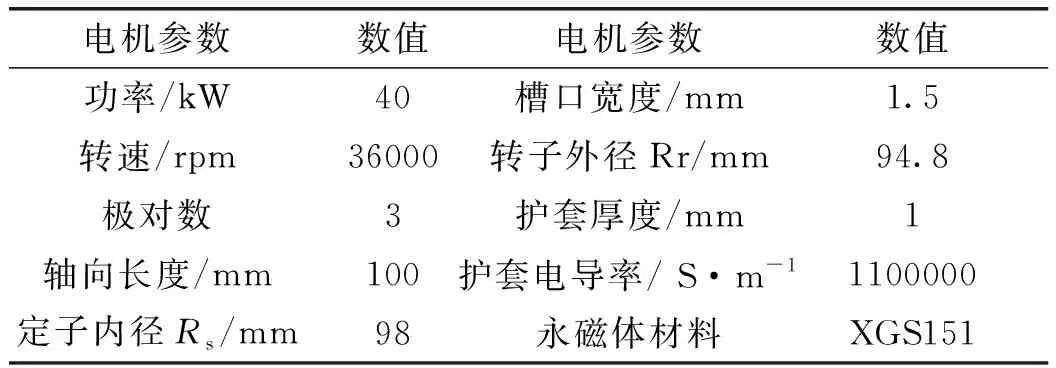
表1 电机的主要参数

为了验证解析模型的正确性，建立有限元模型求解高速永磁电机的转子涡流损耗如图3所示，定子铁心材料选用1J22高饱和磁感应强度铁钴钒软磁合金，1J22材料的B-H曲线如图4所示。空载、额定运行时定子铁心的磁密分布如图5所示。

图3 高速电机剖分图

图4 1J22磁化曲线

图5 定子磁场分布

由图5可知，电机的定子齿尖和齿部会出现局部饱和的现象，而局部饱和会影响电机的磁导谐波变化，改变转子的涡流损耗。分别对气隙磁密和转子涡流损耗进行解析分析，将结果于有限元对比如图6所示。

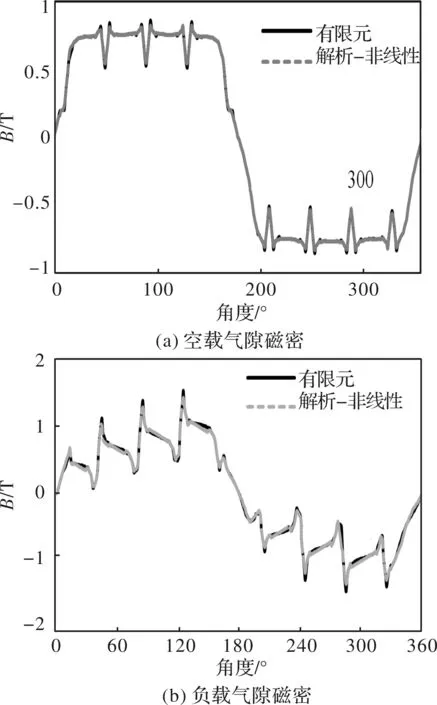
图6 气隙磁密分布

由图6和图7的计算结果可知，该解析模型具有较高的精度，有限元结果和解析结果吻合良好。由损耗计算结果可知，空载和负载时，在考虑定子饱和时转子涡流损耗与定子材料为线性(不考虑饱和)时的损耗结果相比分别相差了约11.8%和13.6%，因此对于高饱和航空高速永磁电机，建立转子涡流损耗解析模型考虑定子非线性是十分必要的。

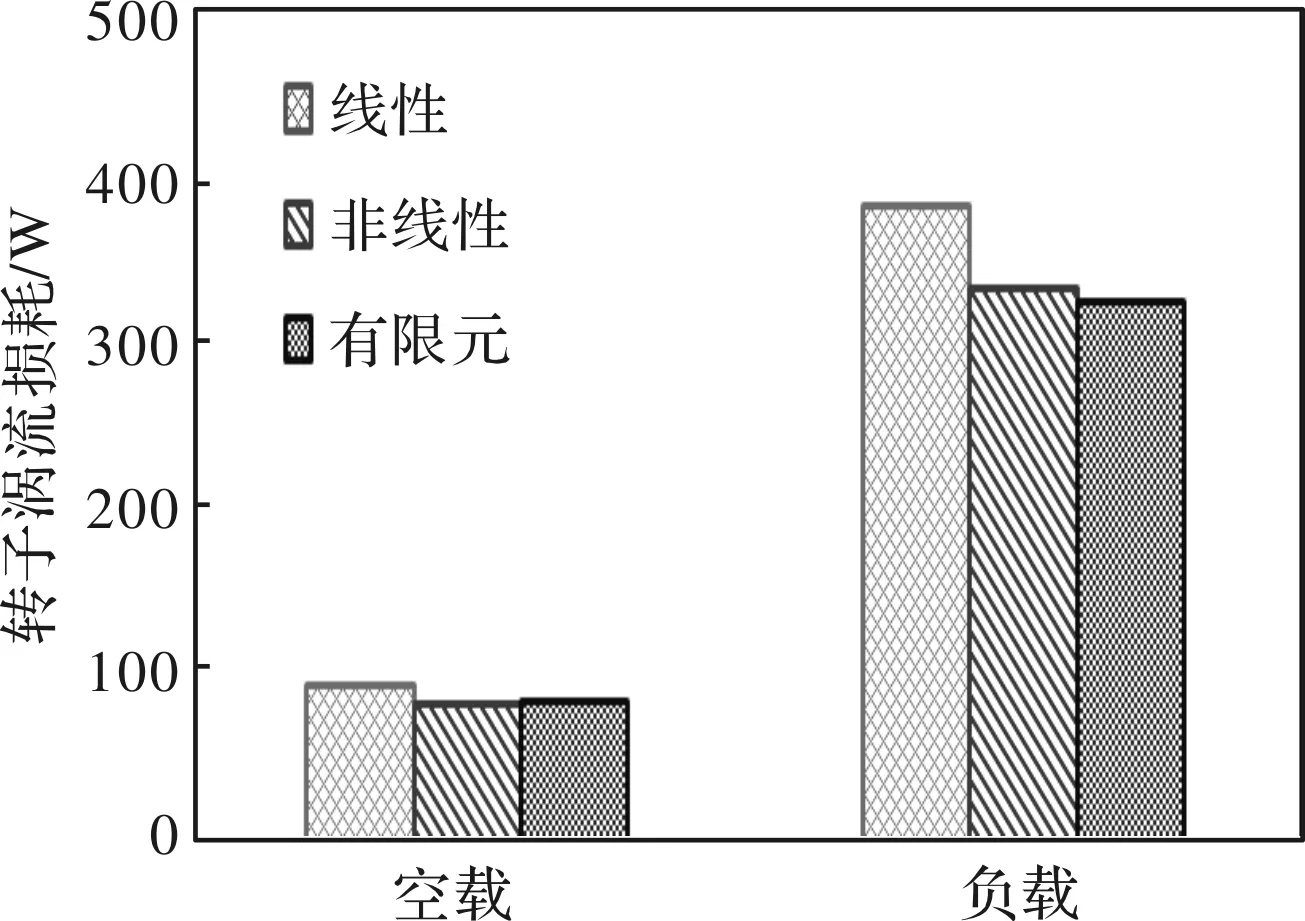
图7 转子涡流损耗对比

2.2 气隙长度对转子涡流损耗的影响

在气隙长度的变化时，为保证电机的性能基本不变，气隙长度变化的同时改变永磁体的厚度，保证空载反电动势基本不变。本文分别对气隙长度为0.3 mm到2 mm时，对转子涡流损耗进行解析分析，通过反电动势校正后，分别计算在考虑饱和以及不考虑饱和时不同气隙长度时转子涡流，并将解析结果与有限元进行对比。如图8所示。

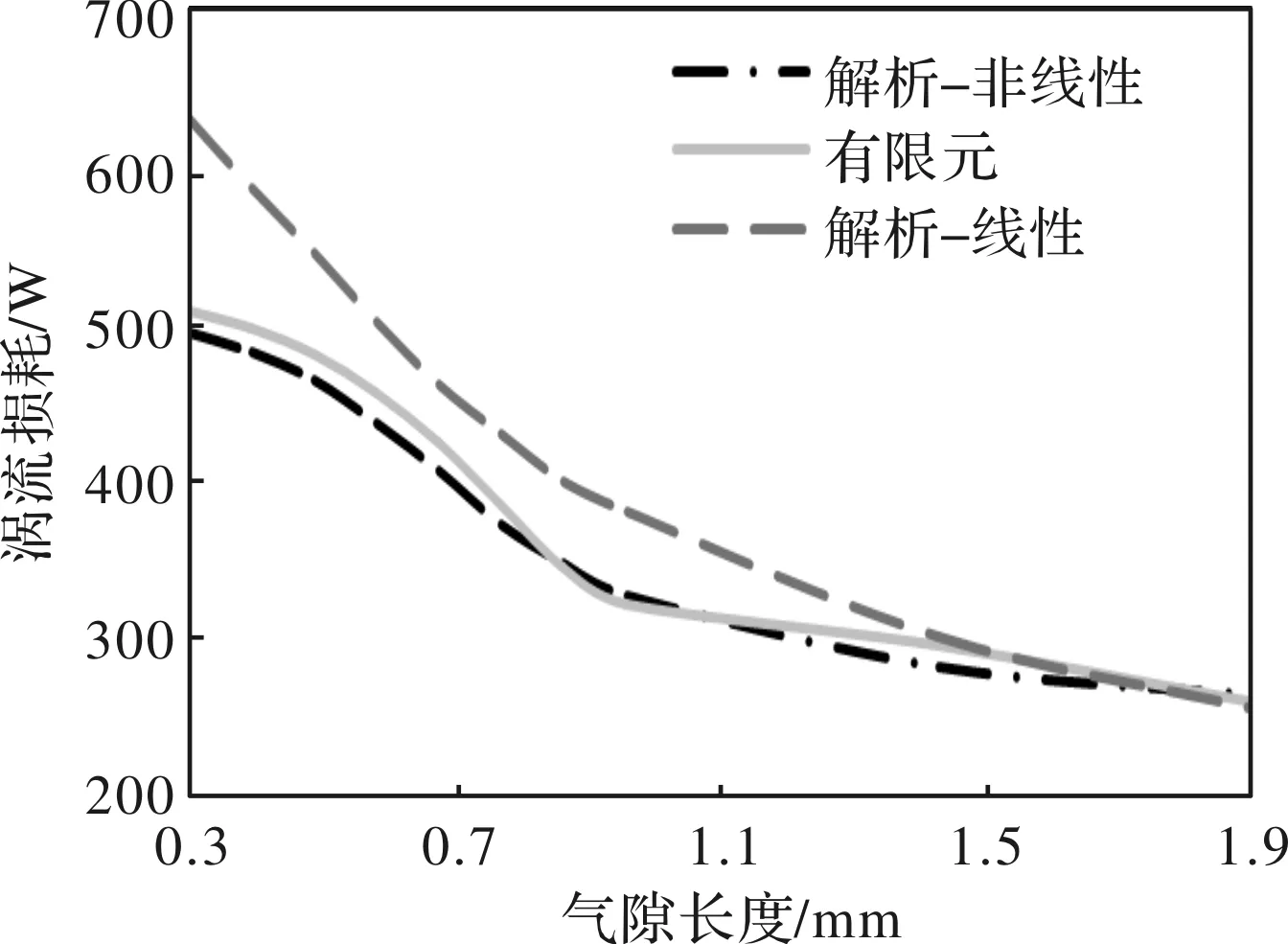
图8 气隙对转子涡流损耗的影响

在气隙长度从0.3 mm增大到2 mm时，转子涡流损耗随气隙长度增大而减小。气隙长度越小，定子饱和对转子涡流损耗影响越大。在不考虑定子饱和时，转子涡流损耗随气隙长度为线性变化。在气隙较大时，可忽略饱和的影响。气隙长度为0.3 mm时考虑定子非线性的损耗与不考虑非线性时相差了19.4%。

2.3 槽口宽度对转子涡流损耗的影响

槽口宽度是抑制转子涡流损耗的有效方法之一。本文分别对针对开口槽、半闭口槽和闭口槽进行分析，计算结果如图9所示。

由计算结果可以看出，采用极限设计的高饱和高速电机，在宽度为0 mm时(闭口槽)与宽度为6 mm时(开口槽)损耗降低了17%。当定子不饱和时，相同条件下，损耗降低了30.6%。这是由于齿尖部分处于高饱和状态，磁导谐波含量变化较小，导致在槽口宽度变化时，转子涡流损耗变化量与普通不饱和高速永磁电机的涡流损耗变化量相比较小。

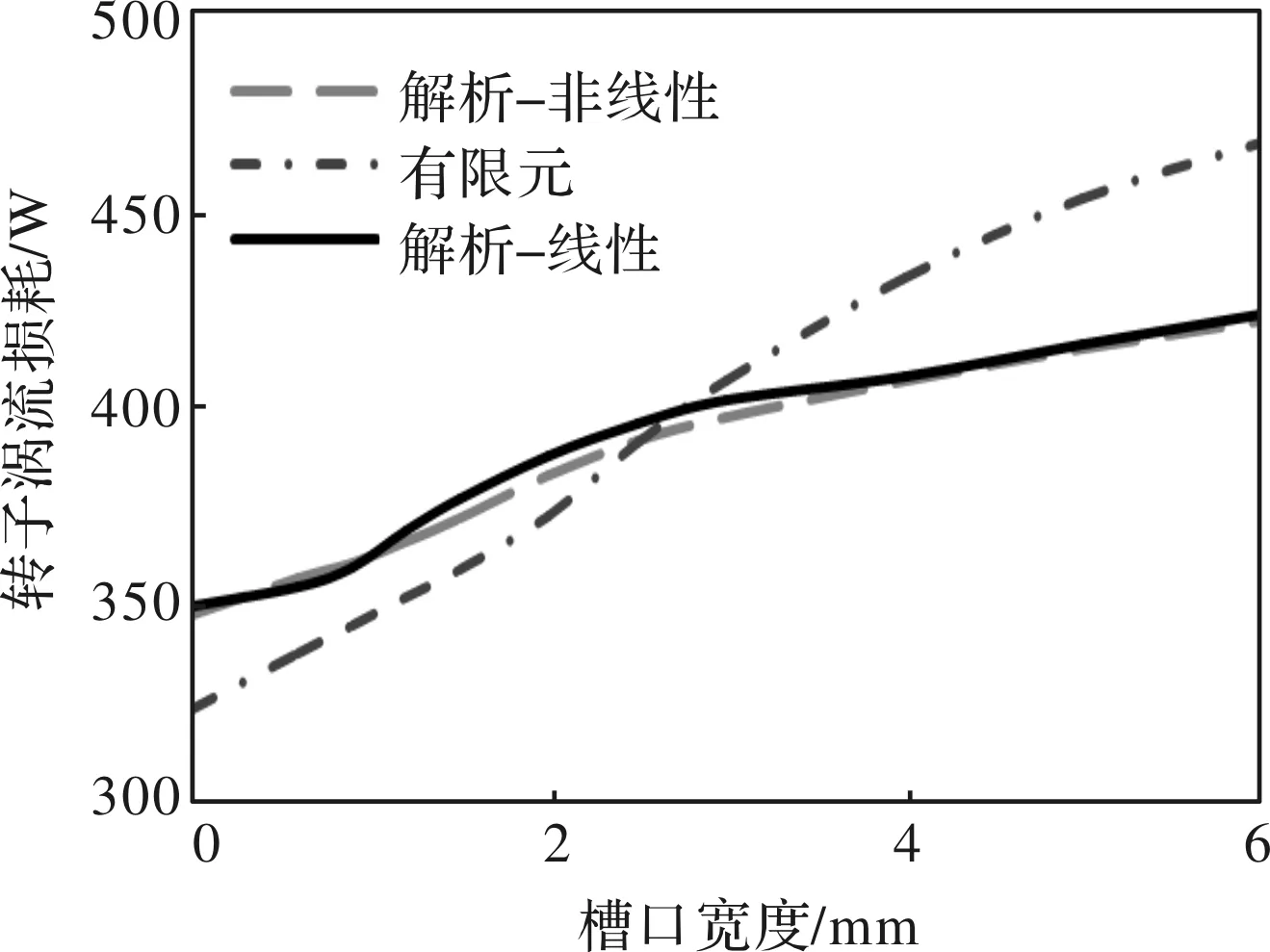
图9 槽口宽度对转子涡流损耗的影响

3 高速永磁电机转子涡流损耗实验

高速永磁电机转子涡流损耗实验测试主要分为热电偶温升测试和损耗分离实验，对于表贴式高速永磁电机安装热电偶困难，而且暂时没有完备的转子涡流损耗直接测量的方法，因此本文采用损耗分离的方法，对一台40 kW，36000 r/min的航空高速永磁电机的转子涡流损耗进行实验测试。实验平台如图10所示。实验流程图如图11所示。

图10 高速电机损耗测试平台

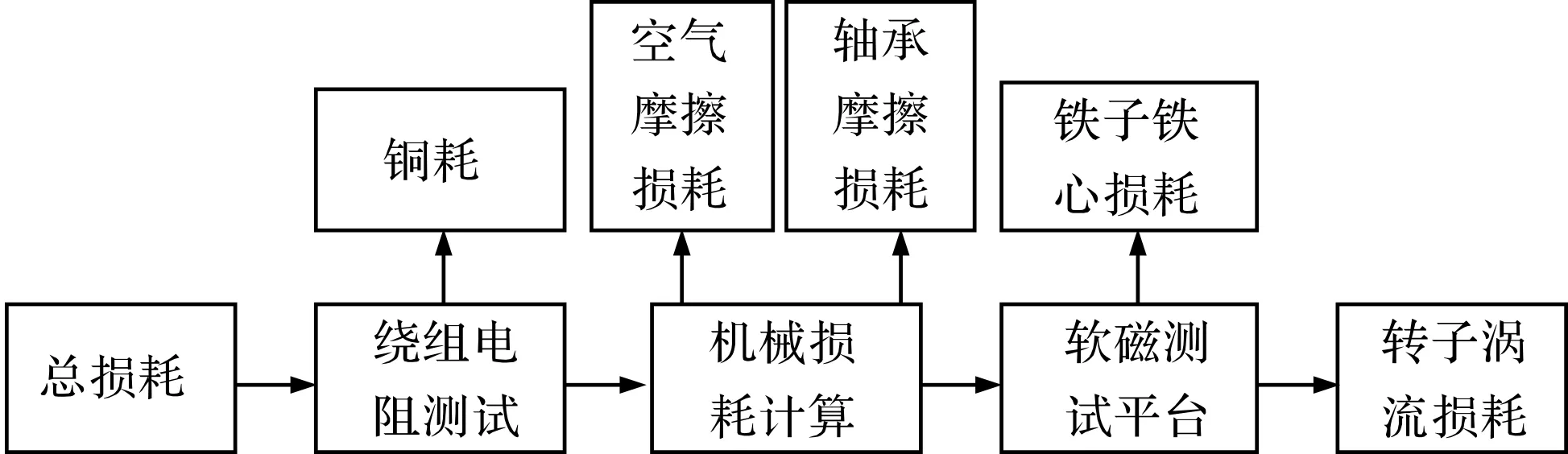
图11 损耗分离流程图

通过上述损耗分离方式得到转子上护套和永磁体的涡流损耗总和。分别在空载不同转速和额定负载条件下对电机进行损耗分离实验。并将解析结果和损耗分离实验的转子涡流损耗实验结果相对比，如图12所示。

从实验结果可以看出，负载实验中，解析结果和实验结果误差较小为4.68%。空载实验中转子涡流损耗存在一定的误差，不同转速下转子涡流损耗的平均误差为8.3%。其主要原因为在于，空载损耗中的转子涡流损耗占比较小，损耗分离时各项误差的累加造成了转子涡流损耗误差增大，但解析计算结果仍然满足工程要求。

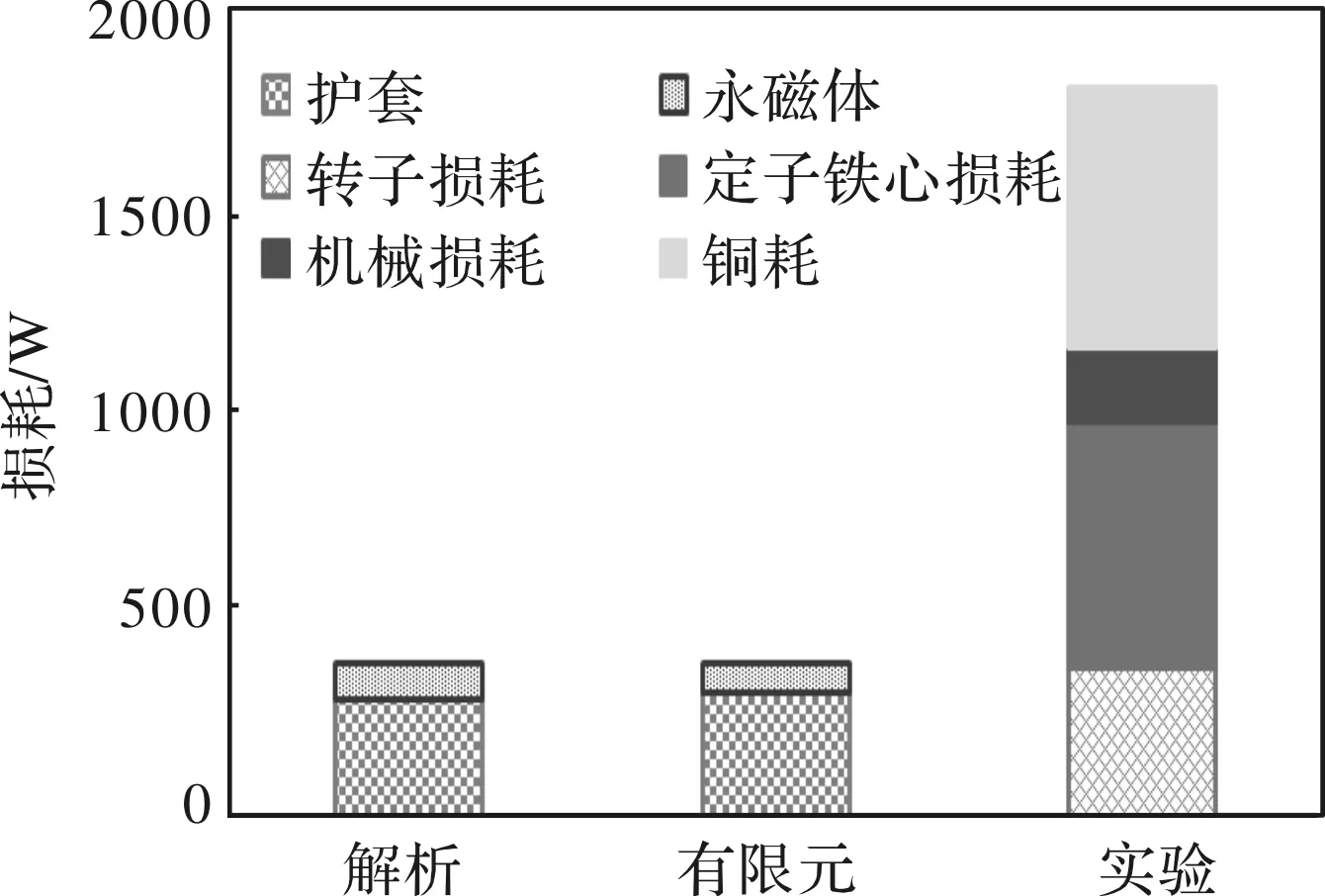
图12 转子涡流损耗实验结果对比

4 结 论

本文将子域法和等效磁路法相结合，针对航空高速永磁电机建立了考虑定子齿轭饱和的转子涡流损耗解析模型。通过对电机空载和额定运行时的磁密和损耗分析验证了该模型具有较高的精度。采用实验的方法对转子涡流损耗进行测试，进一步说明了该模型的准确性。除此之外，该模型对任意极槽配合和时空谐波含量的高速永磁电机都具有良好的通用性。

在电机的气隙长度小时，解析模型中定子铁心非线性对转子涡流损耗的影响较大，考虑定子饱和能够有效的提高计算精度。对于高饱和的高速永磁电机，槽口宽度变化对气隙磁导谐波的影响较小，调整槽口宽度对抑制高饱和航空永磁电机转子涡流损耗的效果不显著。