基于PMSM五阶CKF无传感器控制的EPS仿真研究
张荣芸,郑常胜,朱茂飞,龚长富,时培成,刘亚铭
(1. 安徽工程大学 机械工程学院,安徽 芜湖 241000;2. 杰锋汽车动力系统股份有限公司,安徽 芜湖 241000;3.安徽工程大学 汽车新技术安徽省工程技术中心,安徽 芜湖 241000;4. 合肥学院 先进制造工程学院,安徽 合肥 230601)
0 引 言
转向系统是汽车的重要组成部件,随着汽车电子技术的不断进步,已发展到了现今的电动助力转向系统(Electric Power Steering, EPS)。与其他助力转向系统相比,EPS系统具有体积小、效率高、操纵稳定性好等特点而成为研究热点,并在汽车上得到广泛的应用。EPS系统性能的改善与助力电机的控制性能紧密相关。由于永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有效率高、功率密度大、控制性能好和可靠性高的特点,尤其适用于对空间和节能要求较为严格的汽车上,因此,PMSM已逐渐成为了EPS系统助力电机的主要选择。而PMSM转子位置和转速的准确获取是对其进行良好控制的关键,但常见的利用传感器获得精确转速与转子位置信号的方法,不仅增加了系统结构复杂程度和成本,还导致抗干扰能力降低。因此,对EPS用PMSM进行无传感器控制研究已成为了EPS研究的热点之一。
随着高性能数字信号处理技术的飞速发展,许多学者对PMSM转速估计进行了广泛研究。在零速或低速条件下,常用高频注入法[1]对电机转速进行估计,但该方法需基于电机的凸极效应,且在中高速运转时存在高频噪声,估计精度较低。而在中高速条件下,常用基于模型的观测器法来对电机转速进行估计[2~3]。观测器方法通过建立反电动势或磁链观测器,获得转子位置与转速信息,但在模型搭建的过程中会对电流信号进行微分,这会使噪声信号放大,故需加入滤波环节滤波,增加了算法设计的复杂程度和调试工作量。滑模观测器法是常见的观测器方法,虽然,其具有良好的动态性能,但开关函数的存在却带来了系统抖振问题,影响了估计的精度。另外,还有扩展卡尔曼滤波(Extended Kalman Filter, EKF)算法[4~5]、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)算法[6~7]和容积卡尔曼滤波(Cubature Kalman Fitler, CKF)算法[8~9]。EKF算法具有较好的估计效果,但该方法是通过对非线性系统进行泰勒级数展开取第一项来实现对其线性化的,存在高阶截断误差,同时还需计算复杂的Jacobian矩阵,计算量大实现起来较为困难。UKF算法虽不需计算Jacobian矩阵,但由于在数值计算过程中存在舍入误差,会引起协方差不对称或非正定等不足,容易出现发散。CKF算法通过权值与容积点的计算,经过非线性方程的转换后,产生新的容积点来给出下一时刻的状态估计,不需要对系统进行线性化处理。但CKF算法是基于三阶球面-相径容积规则来近似高斯权值积分的,其估计精度只能达到三阶。
基于上述分析,针对PMSM转子位置和转速估计精度不足的问题,本文提出了一种基于五阶CKF的PMSM无传感器控制方法。首先建立了EPS数学模型,并在基于PMSM数学模型的基础上,通过推导五阶球面-径向容积算法得到五阶CKF算法,利用五阶CKF算法来估计PMSM转子位置和转速信号,构建PMSM的矢量控制系统,实现PMSM无传感器控制。接着将基于五阶CKF无传感器控制的PMSM应用于EPS之中,并进行Carsim/Simulink联合仿真,对所提算法进行仿真验证,仿真结果表明,本文所提算法有较高的估计精度和抗干扰性能,满足EPS对助力电机控制策略的要求。
1 基于PMSM的EPS动力学模型
1.1 EPS动力学模型
本文以管柱式EPS系统作为研究对象,其主要结构包括转向柱、助力电机、转向齿轮齿条及传感器和电子控制单元,如图1所示。

图1 基于PMSM的管柱式EPS系统
对EPS系统进行简化,假设各部件之间润滑良好,忽略各部分之间的摩檫力。对各部分受力分析可得其动力学模型如下:
(1)
Ts=Kc(θc-θp)
(2)
(3)
Ta=g1Km(θm-g1θp)
(4)
(5)

式中,Td、Ts、Tm、TL、Ta分别为驾驶员输入转矩、转矩传感器测量转矩、电机电磁转矩、电机负载转矩、电机提供的助力转矩;Jc、Jm分别为转向柱输入轴转动惯量、电机输出轴转动惯量;Bc、Bm、Br分别为转向柱输入轴阻尼系数、电机输出轴阻尼系数、等效到齿条的阻尼系数;Kc、Km分别为转向柱等效扭杆刚度系数、助力电机输出轴刚度系数;θc、θp、θm分别为转向盘转角、小齿轮转角、电机输出轴转角;g1电机输出轴减速机构传动比;Fr轮胎等效的转向阻力;rp小齿轮半径;M轮胎及齿条等效质量;p齿条位移。
1.2 PMSM助力电机模型
对于EPS用表贴式PMSM,其基于同步旋转坐标系下的数学模型如下:
(6)
式中,ud、uq;id、iq;Ld、Lq;分别为d-q轴的电压、电流和电感;φf永磁体磁链;R为电机定子绕组电阻;pn电机磁极对数;ωm电机转速;B电机阻尼系数;J电机转动惯量;θm电机转角。
对于表贴式PMSM,当采用id=0的控制策略时,电机电磁转矩表达式为
(7)
由式(7)可以看出当电机的磁极对数和永磁体磁链确定后,电机的电磁转矩与q轴电流成正比关系。
将式(6)非线性数学模型转化为状态空间方程形式可描述为

(8)

根据Euler法,将PMSM非线性状态空间数学模型中的状态方程离散化,可得PMSM离散数学模型为
(9)
其中,T为系统采样周期。则式(9)中
根据式(9)建立起的PMSM离散数学模型,可用于五阶CKF算法的推导。
同时,结合式(1)~式(6),将基于PMSM的EPS系统模型转化为状态空间方程的形式,可得

(10)

以转向柱转角作为系统的输入,系统的状态转移矩阵A、输入矩阵B和输出矩阵C,分别为
2 五阶CKF算法
考虑如下非线性离散系统
(11)
式中xk为状态向量,yk为量测向量,且xx∈Rn;yk∈Rm;wk-1与vk是相互独立的零均值系统高斯白噪声和量测高斯噪声,它们的方差分别为Qk-1和Rk。
非线性高斯滤波方法常用来对如式(11)所示的非线性系统进行滤波,但非线性高斯滤波算法的高斯积分在很多时候是不易求得其解析解的。因此,在实际应用中出现了很多方法被用来对该高斯积分进行近似求解,其中,运用三阶球面-相径容积规则来近似的卡尔曼滤波方法就称为容积卡尔曼滤波(CKF)方法。
近年来,具有更高滤波精度的利用五阶球面-相径容积规则来对高斯积分进行近似的方法,被称为五阶容积卡尔曼滤波方法。本文就采用五阶容积卡尔曼滤波方法来实现对EPS系统用PMSM进行无传感器控制,其五阶球面-相径容积规则见2.1。
2.1 五阶球面-相径容积规则
高斯积分可以转化成如式(12)的形式
(12)
式中,f(x)为向量函数或者是矩阵函数。
令x=ry,yTy=1,则xTx=r2,r∈[0,∞]。则式(12)可以转化成一个球面积分和一个相径积分,如式(13)与式(14)所示。
(13)
(14)
式中,Un为n维单位球面,σ(·)为Un上的元素。
采用Gauss-Hermite准则、Spherical准则可将式(12)转化为
(15)
式中,ri与wr,i分别为计算相径积分的点和权值,rj与wy,j分别为计算球面积分的点和权值。Nr与Ns分别是相径积分和球面积分的点数。
对式(15)在求解过程中采用不同的容积规则,能得到不同的积分结果。本文采用五阶球面-相径容积规则来对其求解。
五阶球面规则可记为[10]
(16)
式(16)中权值wy,1与wy,2可表示为
(17)
(18)

(19)
式中,ej为空间Rn的单位矢量,表示第j个元素为1。
由矩匹配法,当Nr=2时的五阶相径规则,积分点和权值需要满足以下条件[11]
(20)
将r1视为自由变量并令其取值为0,则根据式(20)可以得到五阶相径规则的点和权值为
(21)
(22)
根据式(15)、式(16)、式(21)与式(22)可以得到满足标准高斯分布为x~N(x;0,I)的五阶球面-相径容积规则(Nr=2,Ns=2n2),可以表示为
(23)
由式(23)可知,五阶球面-相径容积规则应用了2n2+1个容积点,并且当j=1,2,…,2n(n-1)时,wy,j=wy,1;而当j=2n(n-1)+1,2n(n-1)+2,…,2n2,wy,j=wy,2。
(24)
2.2 五阶CKF算法步骤
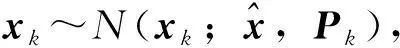
(1)时间更新
①计算容积点xk,i(i=0,1,…,2n2)
(25)

(26)

②将式(25)所生成的容积点,按照状态转移方程进行转移得到新的容积点χk+1/k,i
χk+1/k,i=f(xk,i)
(27)

(28)
其中权值wi可以由式(22)推导得出,如下所示
(29)
④第k+1时刻的状态误差协方差矩阵为Pk+1/k,可表示为
(30)
(2)量测更新
①计算更新后的容积点
(31)

②计算通过测量方程传递的容积点yk+1,i:
yk+1,i=h(xk+1/k,i)
(32)

(33)

(34)
(35)
⑤计算k+1时刻的滤波增益矩阵Kk+1,k:
Kk+1/k=Pxz,k+1/k(Pzz,k+1/k)-1
(36)
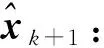
(37)
⑦估计k+1时刻的状态误差协方差阵Pk+1:
Pk+1=Pk+1/k-Kk+1/k(Pzz,k+1/k)(Kk+1/k)T
(38)

图2 五阶CKF的流程图
3 基于PMSM的EPS助力控制
本文考虑的PMSM无传感器控制是采用五阶CKF算法实现的,并且PMSM是应用于汽车EPS系统中的,因此,在确定PMSM输出转矩时要考虑EPS系统的需求,故在设计基于PMSM无传感器控制的EPS系统时,有必要考虑EPS系统转矩控制策略。本文EPS系统转矩控制策略主要考虑其最基本的功能——助力控制,助力控制主要用于车辆在原地或低速转向阻力较大的工况,来提供助力力矩使驾驶员转向轻便舒适。


图3 基于PMSM无传感器控制的EPS系统

4 仿真分析
4.1 基于五阶CKF的PMSM无传感器仿真
在Matlab/Simulink中搭建如图4所示的基于五阶CKF算法的PMSM无传感器控制模型,进行仿真,并和基于CKF的PMSM无传感器矢量控制系统进行对比,来验证本文所提算法的有效性。
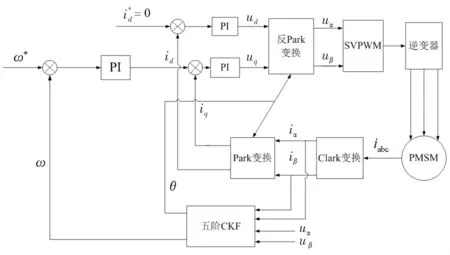
图4 基于5阶CKF的PMSM无传感器控制策略框图
设定电机的主要参数如下:定子电阻Rs=0.958 Ω;定子电感Ls=8.5 mH;磁链φf=0.1827 Wb;转动惯量J=0.003 kg·m2;阻尼系数B=0.008 N·m·s;噪声协方差矩阵为Q=[0.01 0.01 0.21 0.001]T和R=[0.02 0.02]T;极对数pn=4;初始误差协方差矩阵P=[0.5 0.5 0.5 0.5]T。
仿真工况为电机转速由600 r/min上升到800 r/min的转速突变工况。仿真结果如图5~图8所示。

图5 转速估计曲线
图5与图6分别表示转速由600 r/min阶跃到800 r/min时,采用CKF算法和五阶CKF算法对PMSM转速进行估计及其估计误差的对比曲线。由图可知,当转速发生突变时,CKF算法与五阶CKF算法均可以快速的对转速做出稳定准确的估计。而从图6可以看出,五阶CKF算法的转速估计误差在开始时刻和电机转速突变时刻虽有一定的误差峰值,但在电机运行稳定后五阶CKF算法转速估计误差明显小于CKF转速误差,且转速误差具有减小的趋势。因此,仿真说明五阶CKF算法相比于CKF算法具有较高的估计精度及对转速突变也具有更好的适应能力。

图6 转速估计误差曲线

图7 电机转子位置估计曲线

图8 电机转子位置估计误差曲线
图7和图8分别表示转速突变时CKF算法和五阶CKF算法对PMSM的位置估计及其估计误差对比曲线。从图7可知,CKF算法和五阶CKF算法均可以在电机的转速发生阶跃时较好的跟踪PMSM的转子位置。而从图8可以看出,五阶CKF算法在电机稳定运行阶段,转子位置估计误差明显比CKF算法小。因此,仿真表明五阶CKF算法对转子位置的估计也具有更好的估计精度。
4.2 基于五阶CKF的PMSM的无传感器台架实验
为验证所提PMSM无传感器控制方法的实际控制效果,搭建了如图9所示的电机试验台架,试验台主要由上位机、电机驱动试验箱和永磁同步电机组成。在上位机Matlab/Simulink环境中,建立基于CKF和广义五阶CKF算法的PMSM无传感器控制模型,并生成控制模型代码,然后通过CCS6.2编译后生成可在DSP中运行的C代码,再通过仿真器将代码下载到电机试验箱中的TMS320F28335 DSP之中,电机控制箱通过控制逆变器输出驱动信号,控制PMSM工作。上位机可以通过串口工具来接收实验数据,进行参数在线调节,控制PMSM的转速。

图9 电机实验台架
为验证仿真所设置的工况,试验时工况与仿真的一致,即电机转速由600 r/min阶跃到800 r/min的转速突变工况。试验用PMSM参数与仿真时所用参数一致,试验结果如图10~图13所示。
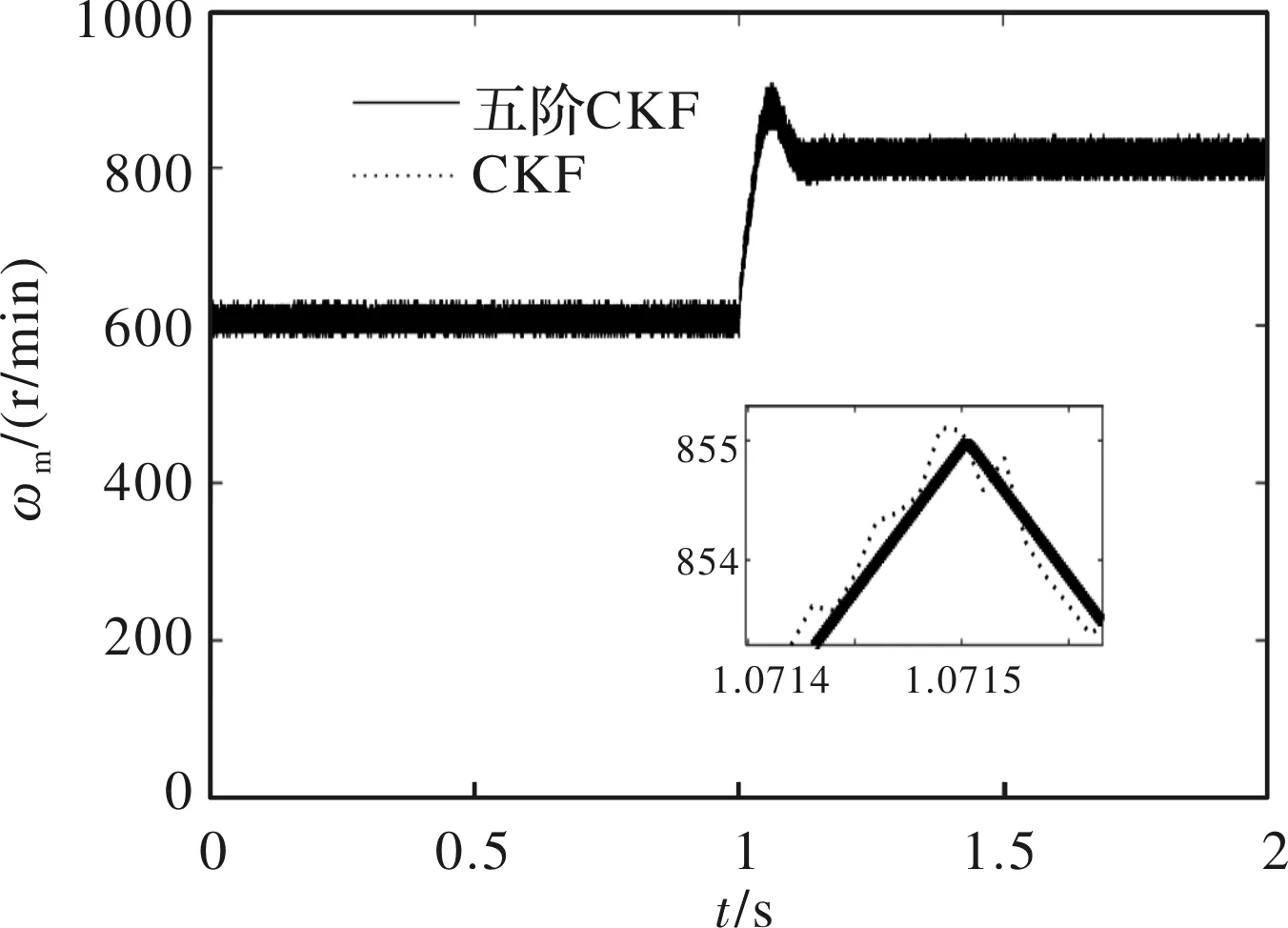
图10 实验转速估计曲线
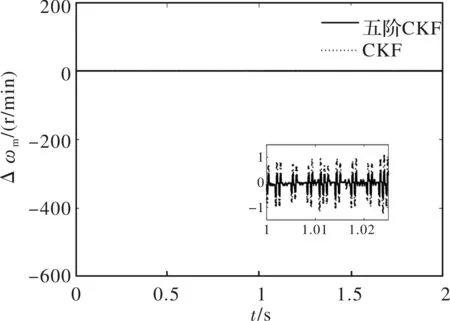
图11 实验转速估计误差曲线
图10和图11为试验时分别采用CKF与五阶CKF算法进行PMSM转速估计及其估计误差的对比曲线。由图可知,在转速阶跃时,五阶CKF算法可以稳定的估计出电机的转速。当电机的转速由600 r/min阶跃至800 r/min时,转速估计误差会有一定增大,但很快稳定下来,并且整个过程中五阶CKF算法的估计误差都较小。因此,实验验证了五阶CKF算法在转速突变时,相较于CKF算法,其估算精度较更高,对转速突变具有较好的适应性。
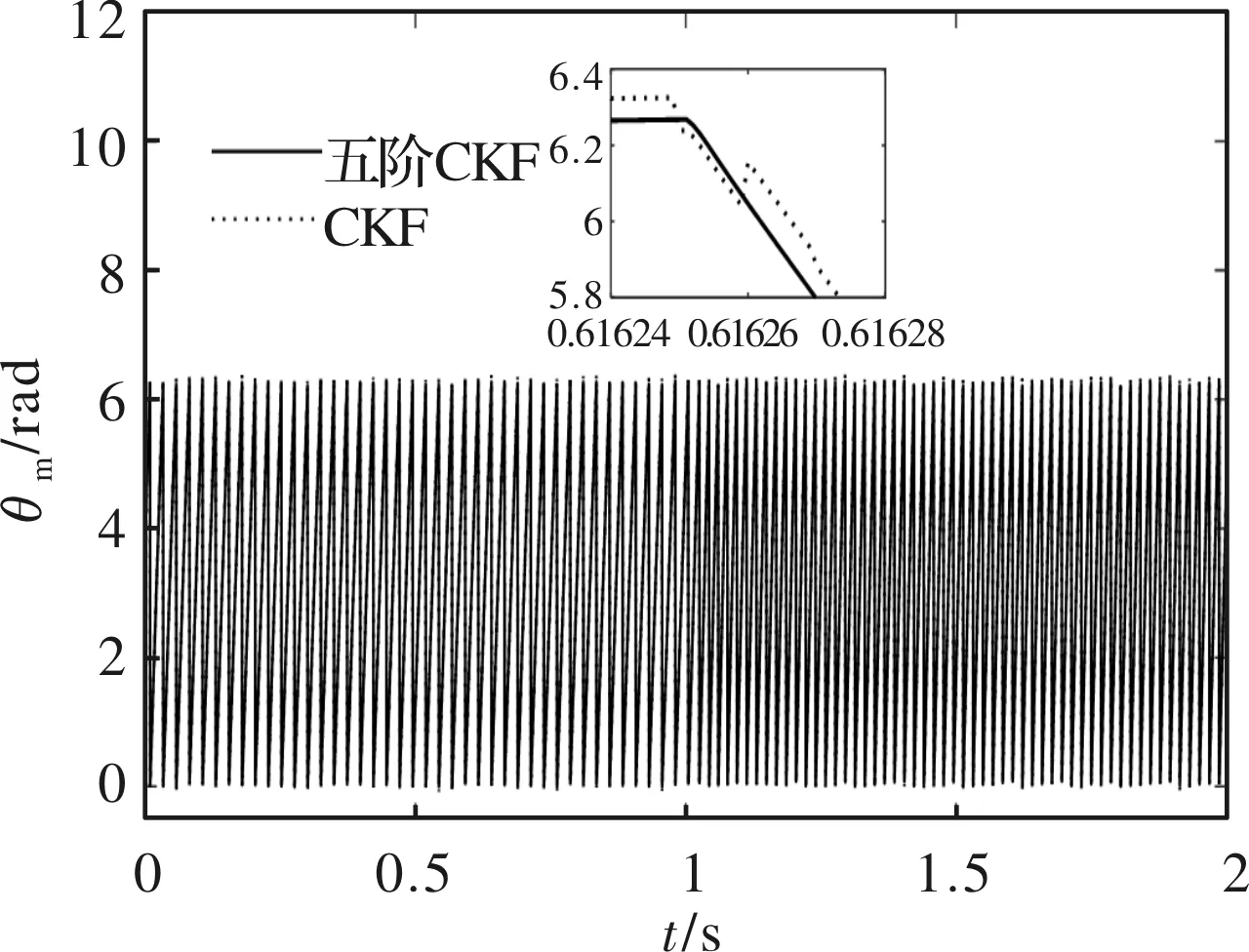
图12 实验转子位置估计曲线

图13 实验转子位置估计误差
图12和图13为试验时分别采用CKF与五阶CKF算法进行PMSM位置估计及其估计误差的对比曲线。由图可知,在实验中,五阶CKF算法可以准确的估计出电机的转子位置,并在转速突变时,其估计精度都要比CKF算法高。因此,实验结果验证了仿真分析的结论,进一步表明了本文所提的利用五阶CKF算法来对PMSM的转子位置进估计的方法,有更高的估计精度。
4.3 基于PMSM的EPS系统Carsim/Simulink联合仿真
根据式(1)~式(5)在Simulink中搭建EPS动力学仿真模型,转向系统模型输入为方向盘输入转矩、助力电机助力矩和转向阻力;输出为转向盘转角、助力电机转角和转向柱转矩。对于整车模型,本文选用专门的汽车动力学仿真软件-Carsim来进行搭建。CarSim具有使用方便、功能强大、仿真结果直观准确等特点而被广泛应用于汽车行业的研究开发。CarSim中包含完善的27自由度整车模型,可以通过S函数实现与Simulink的联合仿真。本文在Simulink中搭建EPS动力学模型及PMSM电机模型。CarSim中的输出量为左右前轮的转向阻力矩和车速,输入为方向盘转角。
模型仿真过程:系统输入转向力矩、电机助力矩和前轮转向阻力,利用EPS动力学模型计算出方向盘转角和转向轴助力矩。在利用车速与转向柱力矩计算出助力电流后,通过控制PMSM的q轴电流来使电机提供相应的助力矩。具体结构如图3所示,其中仿真部分参数如表1所示。

表1 转向系统部分仿真参数
为了验证基于PMSM无传感器控制的EPS系统助力控制效果,对转向系统的转向轻便性进行仿真分析,输入的方向盘转矩为周期是10 s的正弦波信号,分别进行车速为10 km/h,40 km/h和60 km/h的工况进行仿真分析,得到如图14~图16所示的仿真结果。
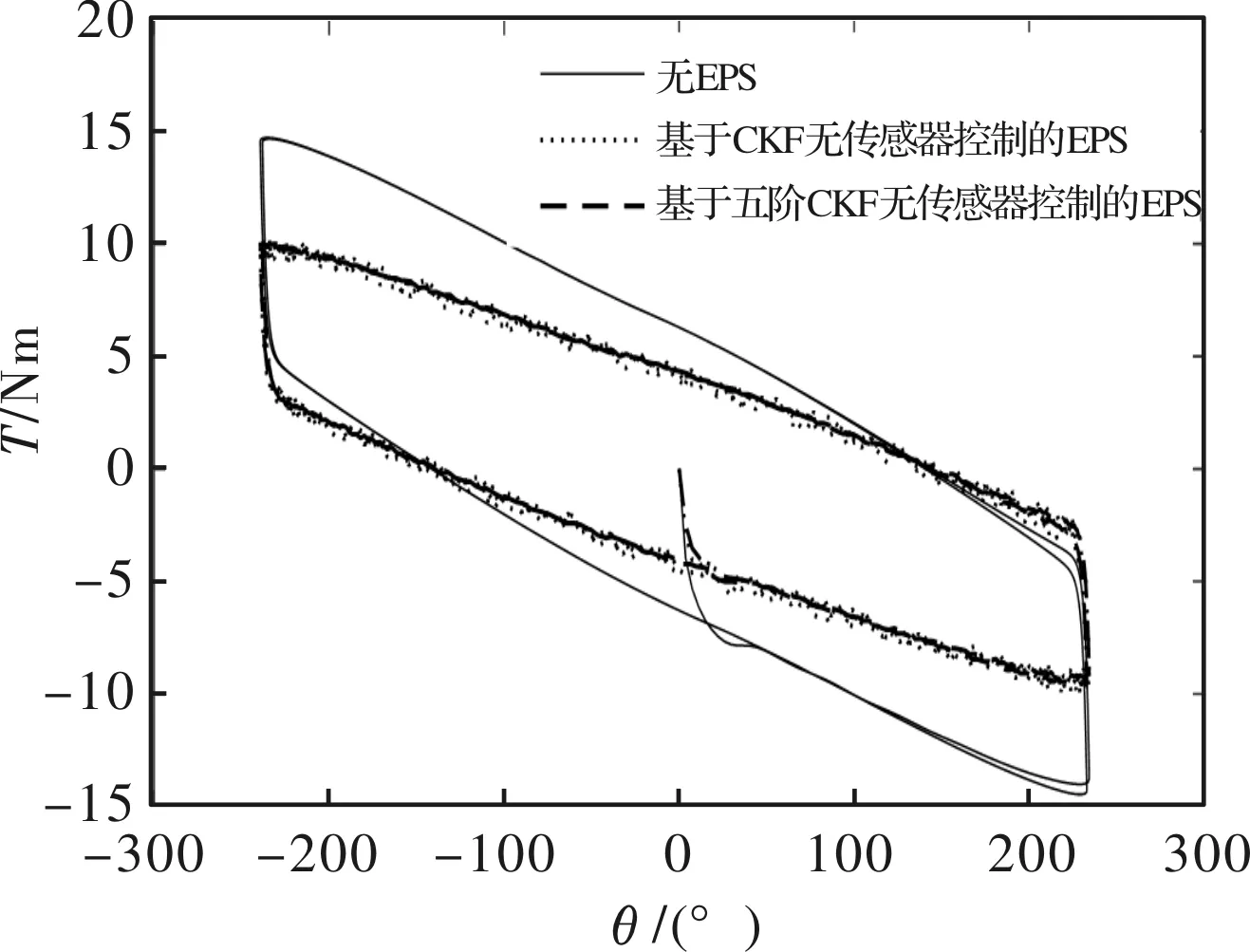
图14 车速为10 km/h时方向盘力矩与转角关系
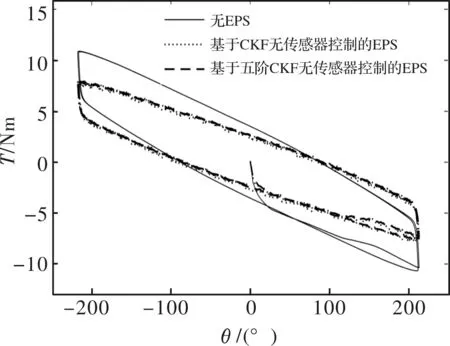
图15 车速为40 km/h时方向盘力矩与转角关系
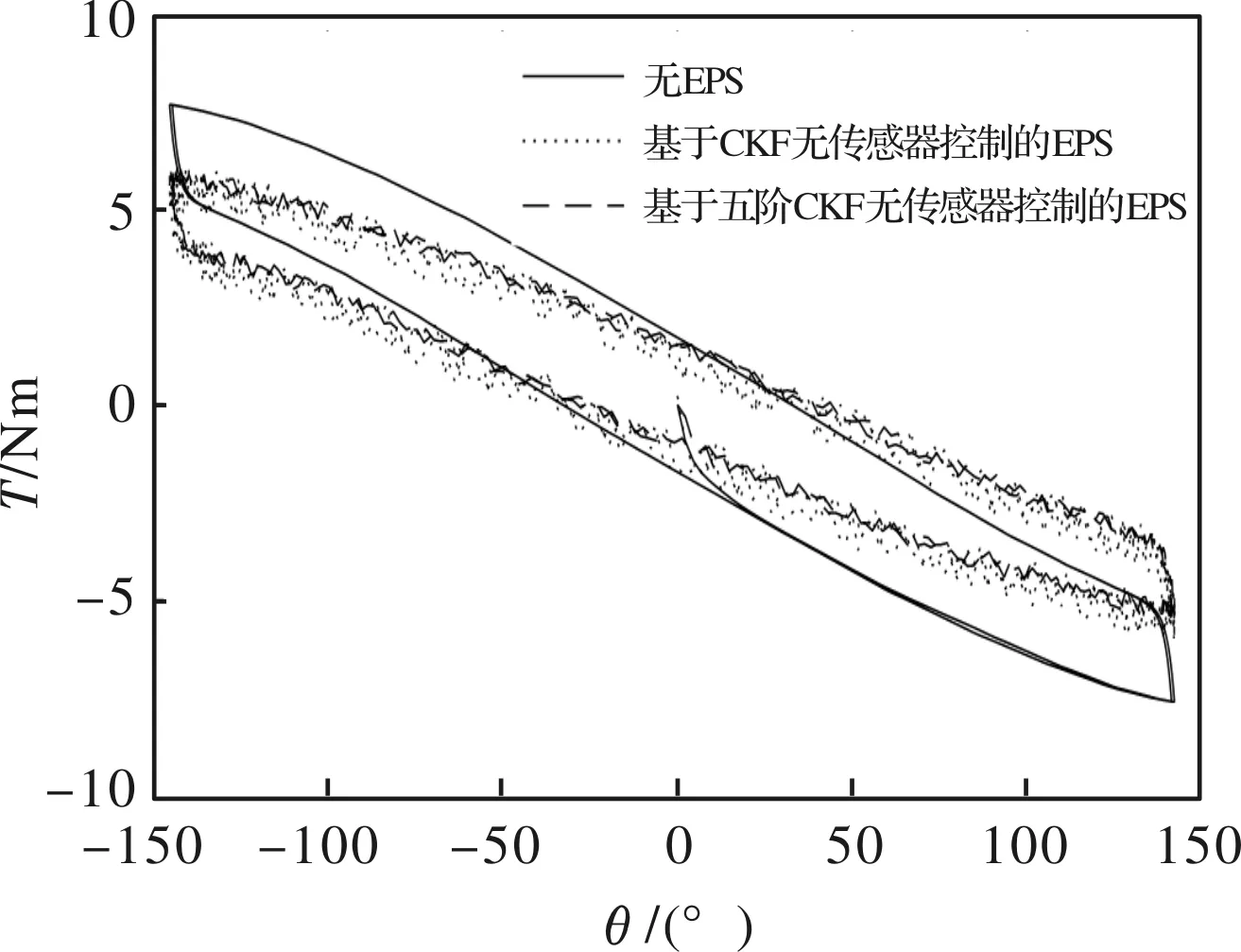
图16 车速为60 km/h时方向盘力矩与转角关系
由上述仿真结果可以看出,基于PMSM无传感器控制的EPS系统可以在不同车速为驾驶员提供稳
定助力,且随着车速的增大方向盘助力转矩逐渐减小,可以为驾驶员提供良好的路感。综上可知,本文设计的基于五阶CKF算法的PMSM无传感器控制可以满足电动助力转向系统在助力模式下对助力电机控制性能的要求,能够减轻驾驶员负担,且具有一定的路感反馈。
5 结 语
本文利用五阶CKF算法实现了PMSM无传感器控制,并结合EPS动力学模型建立了基于PMSM无传感器控制的EPS系统仿真模型。利用CarSim与Simulink联合仿真,对基于PMSM无传感器控制的EPS系统的助力效果进行了仿真验证,仿真结果表明,基于无传感器控制的PMSM满足EPS系统对于助力电机的要求,可以减轻驾驶员负担,提高EPS系统性能,为EPS系统设计提供了新思路和基础。

