双繁星Wiener 指标的极值

李丹怡，陈乌险，晏卫根

（集美大学理学院，福建 厦门361021）

0 引言

设G＝（V，E）是一个连通的简单图，其中，V是顶点集，E是边集。连通图G的Wiener 指标［1］定义为

其中，dG（u，v）表示G中顶点u和v之间的距离。

在图论中，把一个化学分子的原子用顶点表示，原子间形成的化学键用边表示，这样得到的图称为此化学分子对应的分子图［2-3］。分子图的图论不变量可以预测相应分子的物理与化学性质，这种不变量称为分子图的拓扑指标。早在1947 年，Wiener 为了研究无圈分子图的化学性质就提出了图的Wiener 指标的概念［1］，而式（1）则由文献［4］首次提出，以此来预测链烷烃的沸点［1］。文献［4］还发现，Wiener 指标和化合物的化学性质之间有很强的相关性。可以说，Wiener 指标是迄今为止组合（数学）化学中最重要的拓扑指标之一，是数学化学领域（特别是图论）中的一个热门研究问题，得到了许多数学化学家与组合学家的重点关注［5-7］。

目前，关于树（无圈分子图）的Wiener 指标已经有大量的研究结果［7-8］。众所周知，所有n阶树中，星形树Sn和路Pn分别是Wiener 指标最小和最大的树［9］。文献［10］确定了所有给定最大度的n 阶树中Wiener 指标最小的树。文献［11］也给出：在所有给定顶点度序列的n阶树中，贪婪树的Wiener 指标最小，贪婪毛毛虫树的Wiener 指标最大。这里的贪婪树是由贪婪算法得到的树，具体定义参见文献［11］；贪婪毛毛虫树［12］是指具有度序列为（d1，…，dn）（d1≥d2≥…≥dk≥2＞dk＋1＝1）的树，它由给长为k-1 的路v1-v2-…-vk添加悬挂边，使其度序列为d（v1）≥d（vk）≥d（v2）≥d（vk-1）≥…≥d（v［（k＋1）／2］）而得到。如果一个树删去其所有悬挂顶点后得到一条路，则称该树为毛毛虫树。文献［13］刻画了每个顶点的度都为奇数的n阶树中具有最大与最小Wiener 指标的树。

给定两个满足n-1≥d≥2 的正整数n和d，设S1（n，d）是只有一个顶点u的度是d，而其他顶点v（v≠u）的度都不超过2 的n阶树的集合。因此，由S1（n，d）的定义可以看出，S1（n，d）中的树有d条路P1，P2，…，Pd，且它们仅有一个公共顶点u。分别用n1，n2，…，nd表示这d条路P1，P2，…，Pd的长度，则有n-1＝。为了方便，下文中记这种树为T（n；n1，n2，…，nd）。很显然，S1（n，d）＝。文献［14］研究了S1（n，d）中树的Wiener指标与相应的偏序之间的关系，并刻画了这类树的Wiener 指标的极值。

令Sd＋1表示顶点集为｛v0，v1，…，vd｝、中心为v0的星形树。设n1≥n2≥…≥nd是d个非负整数，在Sd＋1中的每个顶点vi（i＝1，2，…，d）上添加ni（ni≥0）条悬挂边，从而得到一个n阶类星树（n＝＋d＋1），记为S（n；n1，n2，…，nd）。文献［15］称这类树为繁星，并解决了繁星的极值能量问题。文献［16］证明了在所有的n阶繁星树S（n；n1，n2，…，nd）中S（n；n-d-1，0，…，0）的Wiener 指标最小，的Wiener 指标最大，其中n-d-1＝kd＋r。

对于两个不相交的星形树Sr＋1和St＋1，其顶点集分别为｛u0，u1，…，ur｝和｛v0，v1，…，vt｝。本文将用一条边连接它们的两个中心点u0和v0而得到的树称为双星，记为Sr，t（t≥r≥1）。例如，双星S2，3如图1 所示。

图1 双星S2，3Fig.1 A double star S2，3

给定两个非负整数n与m，设X＝（n1，n2，…，nr）和Y＝（m1，m2，…，mt）是两个非负整数序列，其中n1≥n2≥…≥nr≥0，m1≥m2≥…≥mt≥0，且满足＝n和＝m。设DSr，t（n，m；X，Y）表示分别在上述双星Sr，t的每个顶点ui（1≤i≤r）上添加ni条悬挂边，在每个顶点vj（1≤j≤t）上添加mj条悬挂边后得到的N阶树，其中N＝r＋t＋n＋m＋2。令DS（r，t；n，m）＝｛DSr，t（n，m；X，Y）＝m｝。一个树T被称为双繁星，若存在4 个满足t≥r≥1、m＋n≥1 的整数r，t，n，m，使得T∈DS（r，t；n，m）。对于2 个非负整数序列X＝（3，1）、Y＝（2，2，1）的双繁星DS2，3（4，5；X，Y）如图2 所示。

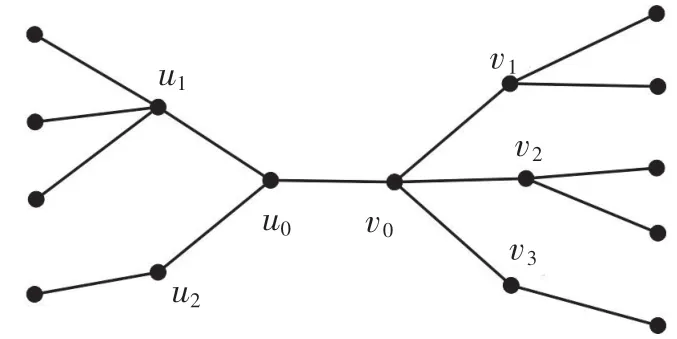
图2 双繁星DS2,3(4,5;X,Y)（X=(3,1)，Y=(2,2,1)）Fig.2 A blossomed double star DS2,3(4,5;X,Y)for X=(3,1)and Y=(2,2,1)

本文考虑DS（r，t；n，m）中双繁星Wiener 指标的极值问题，刻画了具有最小Wiener 指数的双繁星。

1 主要结果及其证明

首先介绍一个关于Wiener 指标方面的重要结果。

引理1［1］设T是一个边集为E的树，则T的Wiener 指标

其中：求和中e跑遍T的所有边；nx（e）表示T-e中包含顶点x那个分支的顶点数，T-e是从T中删去边e所得的子图。

本文还需要证明以下引理2 和引理3，它们将在后面主要结果的证明中起关键作用。

引理2设DSr，t（n，m；X，Y）是一个N＝r＋t＋2＋n＋m阶双繁星，其中X＝（n1，n2，…，nr），Y＝（m1，m2，…，mt）。对于给定的正整数i与j（1≤i＜j≤r），如果有ni-nj≥2，设X′＝（n1，…，ni-1，…，nj＋1，…，nr），那么

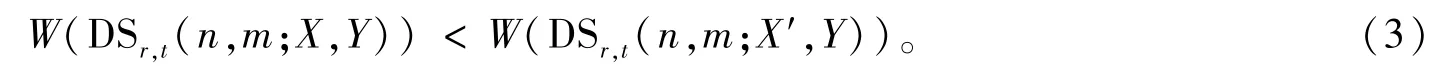
相似地，对于给定的正整数k，l（1≤k＜l≤t），如果mk-ml≥2，可以令Y′＝（m1，…，mk-1，…，ml＋1，…，mt），那么

证明设T＝DSr，t（n，m；X，Y），T′＝DSr，t（n，m；X′，Y）。对T与T′，利用引理1，不难得到：W（T）-W（T′）＝（ni＋1）（N-ni-1）＋（nj＋1）（N-nj-1）-ni（N-ni）-（nj＋2）（N-nj-2）＝-2（ni-nj-1）。因为ni-nj≥2，因此W（T）-W（T′）＜0。

同理可以证明式（4）的不等式成立。故引理2 得证。

引理3设DSr，t（n，m；X，Y）是一个N＝r＋t＋2＋n＋m阶双繁星，其中X＝（n，0，…，0），Y＝（m，0，…，0）。如果n≥1，m-n≥（r-t-3）／3，令X′＝（n-1，0，…，0），Y′＝（m＋1，0，…，0），那么W（DSr，t（n，m；X，Y））≥W（DSr，t（n-1，m＋1；X′，Y′）），当且仅当m-n＝（r-t-3）／3 时等号成立。

证明设T＝DSr，t（n，m；X，Y），T′＝DSr，t（n-1，m＋1；X′，Y′）。由引理1 可知：W（T）-W（T′）＝（n＋1）（N-n-1）＋（n＋r＋1）（m＋t＋1）＋（m＋1）（N-m-1）-n（N-n）-（n＋r）（m＋t＋2）-（m＋2）（N-m-2）＝N-n-n-1-（n＋r）＋t＋m＋1＋m＋1-（N-m-2）＝3m-3n＋t-r＋3。显然，若m-n＞（r-t-3）／3，有W（T）-W（T′）＞0；若m-n＝（r-t-3）／3，有W（T）＝W（T′）。引理3 证毕。

下面证明本文的3 个主要结论定理1～定理3。

定理1对于4 个固定的非负整数r，t（t≥r≥1），n，m（m＋n≥1），在集合DS（r，t；n，m）中，双繁星DSr，t（n，m；X°，Y°）的Wiener 指标最小，其中。

证明假设当X°＝（n1，n2，…，nr）、Y°＝（m1，m2，…，mt）时，集合DS（r，t；n，m）中双繁星DSr，t（n，m；X°，Y°）的Wiener 指标最小。对给定的整数n＝，若对1≤i＜j≤r，存在ni≥nj≥1，即（ni＋1）-（nj-1）≥2，可以令X′＝（n1，…，ni＋1，…，nj-1，…，nr）。那么，由引理2，可得W（DSr，t（n，m；X′，Y°））＜W（DSr，t（n，m；X°，Y°）），这与假设矛盾。

同理，给定整数m＝，对任意i，j（1≤i＜j≤t），不存在整数对mi和mj，使mi≥mj≥1。因此，在给定非负整数r，t，n，m的情况下，集合DS（r，t；n，m）中DSr，t（n，m；X°，Y°）的Wiener 指标最小，其中。于是定理1 成立。

当r，t，n，m都是固定的整数时，定理1 刻画了DS（r，t；n，m）中具有最小的Wiener 指标的双繁星为DSr，t（n，m；X°，Y°）。

对3 个固定的正整数r，t（t≥r≥1），n＋m，定义DS（r，t；n＋m）为所有满足条件x＋y＝m＋n的双繁星集DS（r，t；x，y）的并集，即DS（r，t；n＋m）＝。当r，t，n＋m都是固定的整数时，下面的定理2 刻画了DS（r，t；n＋m）中具有最小的Wiener 指标的双繁星。

定理2对固定的正整数r，t（t≥r≥1），n＋m，则DS（r，t；n＋m）＝：∪｛＝n＋m｝中双繁星DSr，t（0，n＋m；X*，Y*）的Wiener 指标最小，其中。

证明给定非负整数r，t（t≥r≥1），n＋m，注意到DS（r，t；n＋m）是所有满足x＋y＝n＋m的集合DS（r，t；x，y）之并。为了讨论DS（r，t；n＋m）中具有最小Wiener 指标的双繁星，可以分为以下3个步骤：

证明给定正整数r＋t和n＋m，注意到DS（r＋t；n＋m）是所有满足x1＋x2＝t＋r，1≤x1≤x2的集合DS（x1，x2；n＋m）之并。

综上，在给定非负整数r＋t、n＋m的情况下，集合DS（r＋t；n＋m）中DS1，r＋t-1（0，n＋m；X°，Y°）的Wiener 指标最小，其中X°＝（0），Y°＝。

2 结论

本文考虑了所谓的双繁星的最小Wiener 指标问题。此外，确定双繁星的最大Wiener 指标和能量、谱半径等许多其他拓扑指标的极值问题也是一件非常有意义的工作。而且，双繁星是一类直径为4 或5 的无圈分子图，而无圈分子图拓扑指标的极值问题可以应用于理论化学中所谓的定量结构-性质关系和定量结构-活性关系的设计，因此也具有很好的研究意义。