油气悬挂囊式蓄能器气体迟滞环特性分析

杨岳霖，王云超，胡志超

（集美大学海洋装备与机械工程学院，福建 厦门361021）

0 引言

油气悬挂由于其非线性刚度特性被广泛应用于各工程领域，如车辆悬挂系统、精密加工设备及座椅悬架等［1-2］。车辆中悬挂系统的输出特性直接影响整车性能［3］，准确可靠的油气悬挂仿真模型是研究油气悬挂特性和整车性能的基础，具有重要的现实意义和应用价值［4］。蓄能器作为悬挂系统的重要元件其氮气多变过程模型的精度是油气悬架系统特性分析的关键因素［5-6］，因此对蓄能器特性进行分析是油气悬挂系统研究的基础。

大多研究者利用悬挂油缸的输出力-位移曲线或压力-位移曲线（迟滞环）对油气悬挂系统的刚度和阻尼进行研究［7-10］。迟滞环的刚度反映了悬挂系统的刚度，迟滞环的开度则代表了悬挂系统阻尼，因此迟滞环的各项特性就反映了蓄能器及悬挂系统的特性［11-12］。大部分悬挂系统研究都是基于理想气体多变过程建立的蓄能器及油气悬架系统模型，而实际蓄能器氮气的多变过程不同于理想气体多变过程。为此，众多学者针对实际气体的多变过程进行了深入的研究，主要集中在2 个方面：1）从热传递和能量守恒角度研究蓄能器的多变过程。如Otis［12］等建立了热对流模型来描述气体热动力学过程，并建立了一个热时间常数模型；Pourmovahed［13］等提出了一种基于试验数据的热时间常数关联模型用于预测蓄能器气体压力和温度变化；Westhuizen［14］等对比分析了理想气体模型和实际气体模型的实用性，认为应该根据实际需要选择合适的模型，但由于热时间常数难以确定，需要通过实验测量获得［15］，因此，建模存在困难，并且以上研究对象全是活塞式蓄能器，而油气悬挂系统中普遍采用的囊式蓄能器的研究却鲜有报道。2）从理论和试验角度研究蓄能器的气体多变过程指数。如封士彩［16］、王德伟［17］等试图通过理论推导和试验方法确定气体多变过程指数的实际取值，由于其研究是基于理想气体多变过程获得的结果，与实际还存在一定的误差；王云超等［18］、魏彬［19］基于蓄能器正弦激振试验结果，提出了一种基于体积压缩率和体积压缩速率的真实气体多变指数模型，但其仅针对低频工况，缺乏高频工况的验证。

综上所述，为了探究囊式蓄能器的特性，描述气体多变过程，实现蓄能器内气体的准确建模，本文对油气悬挂系统中囊式蓄能器进行更加深入地试验研究，分析影响蓄能器阻尼和刚度特性的关键因素，提出一种基于迟滞时间的真实气体多变过程指数模型，并进行仿真和试验验证。

1 囊式蓄能器试验平台

1.1 试验原理

为了测试油气悬架中囊式蓄能器的性能，搭建囊式蓄能器性能试验平台，如图1 所示。该试验平台的原理如图2 所示。

图1 囊式蓄能器试验平台Fig.1 Platform for bladder accumulator

图2 囊式蓄能器试验平台原理图Fig.2 Schematic diagram of the test rig

伺服阀接收控制信号后控制激励油缸，使激励油缸驱动被动油缸按照正弦规律运动。此时被动油缸无杆腔内的油液在活塞的作用下进入蓄能器，使蓄能器实现充油、放油的过程。通过油路中和蓄能器上的温度-压力传感器，采集油液和气体的压力、温度。试验台的主要参数如表1 所示。

表1 囊式蓄能器试验平台主要参数Tab.1 Main parameters of the test rig

1.2 试验仪器及试验方案

本次试验采用的主要仪器设备见表2。

表2 囊式蓄能器试验平台主要仪器Tab.2 Main instruments of the test rig

实验方法：被动油缸在激励油缸的驱动下实现不同频率的正弦激励，通过观察蓄能器内气体压力随外部激励的变化规律，进一步分析蓄能器的迟滞特性及影响因素。

实验初始条件：蓄能器初始充气压力为2.22 MPa；初始平衡压力为3.34 MPa；实验环境温度为27 ℃；初始气体温度为27 ℃。

根据试验台的工作范围确定进行振幅为15 mm，频率分别为0.25、0.50、1.00、1.50、2.00、2.50、3.00 Hz 的正弦激励试验。

2 试验结果分析

为了便于试验分析，采用文献［18］中体积压缩率的定义：η＝-ΔV／V0。式中：V0为蓄能器的额定体积（L）；ΔV为蓄能器内的氮气体积变化量（L），ΔV＝A·S；A，S分别为被动油缸的无杆腔面积（cm2）和位移量（cm），S也等于激励油缸的位移（被动油缸被压缩为正，即气囊被压缩时位移为正）。

由图3 可知，随着激振频率的升高，蓄能器内气体的迟滞环面积逐渐增大而刚度逐渐减小。由于迟滞环的面积大小反映蓄能器的阻尼特性，迟滞环刚度则反映了蓄能器的刚度特性，从以上试验结果可以看出，蓄能器的氮气多变过程存在较大的阻尼。因此，假设蓄能器内的氮气多变过程为理想气体多变过程是不合适的，需要进行深入的研究。

图3 不同激励频率的正弦激励结果Fig.3 Experimental results of sinusoidal excitation with different frequencies

2.1 囊式蓄能器的阻尼特性

2.1.1 阻尼特性的关键影响因素

一般来说，悬挂系统的阻尼有两大影响因素：1）流体摩擦，也叫做黏性摩擦。在油缸与蓄能器之间存在阻尼孔等阻尼元件，当油液通过时产生压力损耗，将油液的动能转换为热能消散，进而产生黏性阻尼力；2）边界摩擦。在油缸运动过程中，缸杆、活塞和缸筒内壁与油液之间存在摩擦，这种摩擦起到了阻尼的效果。

在该囊式蓄能器试验平台中，油缸与蓄能器之间并无阻尼孔等阻尼元件，且连接件造成的阻尼及边界阻尼较小，造成的影响基本可忽略不计，因此，迟滞环的开度应该由蓄能器自身阻尼特性或气体特性决定［19］。

为了分析造成囊式蓄能器阻尼过大的影响因素，对试验结果进行了深入的对比分析后发现：蓄能器内气体压力变化曲线滞后于激励位移变化曲线。图4 所示为振幅为15 mm，激振频率分别为0.25、1.00、2.50 Hz 正弦激振试验激励油缸位移和气体压力变化曲线。

图4 体积压缩率与气体压力变化曲线Fig.4 Variation curves of volume compression ratio and gas pressure

由图4 可以看出，气体压力变化滞后于激励油缸位移变化，并且随激振频率增加，滞后现象更加明显，说明蓄能器的氮气压力滞后程度与激振频率呈一定的正比关系。

2.1.2 迟滞时间对迟滞环的影响

为了分析迟滞时间对迟滞环的影响，对比分析了有、无迟滞时间的蓄能器氮气多变过程，如图5所示。正弦激励的振幅为15 mm，激振频率为1.00 Hz、2.50 Hz 的有、无迟滞时间的迟滞环对比结果分别如图5a、图5b。从图5 可以明显看出，气体压力的迟滞时间是造成迟滞环开度的主要原因。无迟滞时间的蓄能器特性曲线基本无阻尼，近似理想气体的多变过程。因此，在建立真实气体多变指数模型时，应将迟滞时间作为决定迟滞环的关键影响因素。

图5 有、无迟滞时间的迟滞环对比Fig.5 Comparison of hysteresis loop(consider or eliminate hysteresis)

2.2 囊式蓄能器的刚度特性

由悬挂系统的工作原理可知，在悬挂系统工作时，对刚度产生单独影响的因素有3 个：1）蓄能器内气体压缩率；2）油液压缩率；3）管路等部件的弹性。但由于液压油的弹性模量和管路等连接件的刚度通常很高，对悬挂系统的刚度影响很小，这意味着悬挂系统的刚度特性主要受蓄能器内氮气特性的影响。

2.2.1 体积压缩率对气体多变过程的影响

为了进一步分析无迟滞时间的蓄能器的气体多变过程，对比了理想气体的等温、绝热过程和无迟滞时间的真实气体的多变过程，如图6 所示。从图6 可以看出，与理想气体的等温和绝热过程相比，不考虑迟滞时间的真实气体多变过程，气体变化更加明显。这也证明了实际气体多变过程的多变过程指数是一个过程变化量，不同的体积压缩率对应不同的多变过程指数，如图7 所示。由于文献［18］中实验采用的激振频率和激振幅值较小，因此认为气体压缩率与气体多变指数呈一定线性关系，但从图7 可以看出，消除迟滞时间的影响后，气体压缩率与气体多变指数呈二次函数关系。图8 所示为理想气体多变过程与无迟滞时间的真实气体多变过程对比。从图8 可以看出，当理想气体多变过程指数随体积压缩率按照一定规律变化时，理想气体多变过程与无迟滞时间的真实气体多变过程十分吻合，表明蓄能器的体积压缩率是气体多变过程指数的主要影响因素之一。

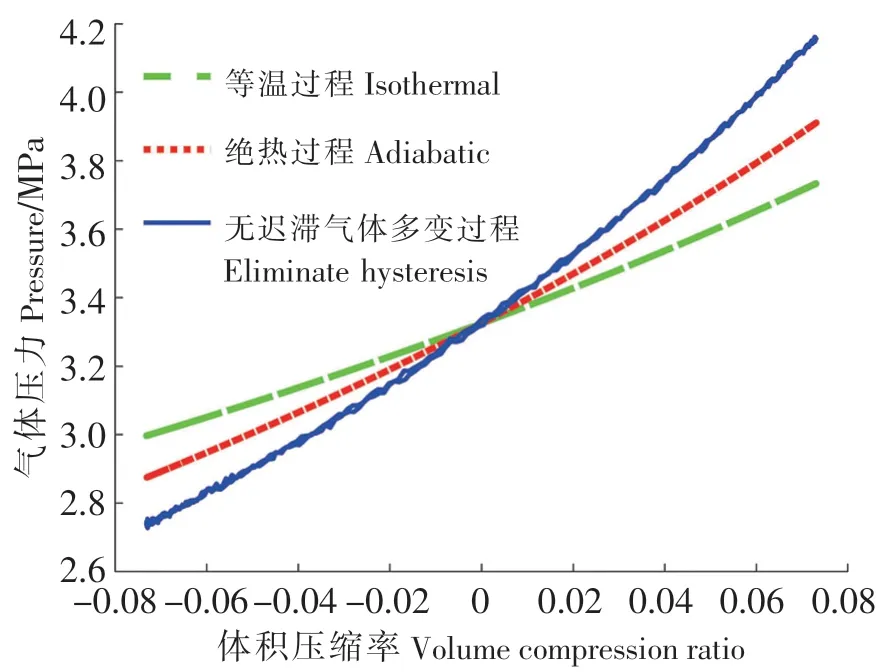
图6 真实气体多变过程与理想气体等温、绝热过程对比Fig.6 Real gas polytropic process versus ideal gas process

图7 不同频率下迟滞气体多变指数（消除迟滞）Fig.7 The polytropic index of gas with different frequencies(eliminating hysteresis)

图8 理想气体多变过程与无迟滞真实气体多变过程对比Fig.8 Comparison between polytropic process of ideal gas and real gas

2.2.2 激振频率对气体多变过程的影响

为了分析激振频率对气体多变过程的影响，图9 对比分析了振幅为15 mm，不同频率的无迟滞时间的蓄能器气体多变过程。从图9 可以看出，当激振频率小于2.00 Hz 时，不同激振频率对气体多变过程的影响很小；当激振频率大于2.00 Hz 时，随着激振频率的增加，气体多变过程的斜率有所减小。分析其原因，可能是激振频率提高导致蓄能器与外界的热传递减少造成的。

图9 不同激振频率的蓄能器气体多变过程Fig.9 Polytropic process of gas with different excitation frequencies

2.2.3 气体多变过程指数的体积压缩率系数

气体多变过程指数的体积压缩率系数等效于蓄能器的刚度系数。该系数的取值，由体积压缩率的最小和最大值对应的气体多变指数连线的斜率决定［18］。由于体积压缩率与气体多变指数呈二次函数关系，因此体积压缩率系数为体积压缩率的一次函数。

综上所述，本文分析了迟滞时间、激振频率和体积压缩率对蓄能器气体多变过程指数的影响分析，提出气体多变过程指数的体积压缩率系数为：

k＝a·ηt＋b。

式中：a、b为不同激振频率下体积压缩率系数常数，取值如表3 所示；ηt为考虑迟滞时间的蓄能器气体瞬时体积压缩率，ηt＝-Vt／V0，Vt为考虑迟滞时间的蓄能器气体的瞬时体积，Vt＝St·A，St为考虑迟滞时间的激励油缸的位移。

表3 不同激振频率下体积压缩率系数常数取值Tab.3 Coefficient of volume compression ratio with different excitation frequencies

3 真实气体多变指数模型验证

根据前文的分析，对文献［18］中真实气体多变指数模型进行修改：

其中：P为蓄能器内气体瞬时压力，（MPa）；P0为蓄能器的初始充气压力（MPa）；V0为蓄能器的额定体积（m3）；k为气体多变指数体积压缩率系数。

为了验证模型的正确性，将各个工况测得的ηt及不同激振频率下的a、b带入公式（1），将模型仿真结果与试验数据进行对比，结果如图10 所示。

图10 正弦激励下气体模型预测值与试验数据对比Fig.10 Comparison between predicated gas pressure and test data under sinusoidal excitation

不同频率的仿真模型预测值和测试数据的误差如表4 所示。从表4 可知，预测值与试验结果的整体平均误差为4.2%，激励频率为3.00 Hz 时误差最大为8.7%，该误差是采集频率不足造成的。但从整体仿真模型预测结果和测试数据的对比中可以看出，真实气体多变指数模型能够较好地跟踪真实气体的多变过程，该模型的建立为进一步准确建立油气悬挂系统的模型奠定了基础。

表4 不同激振频率下预测值与试验数据的误差Tab.4 The discrepancy between predicated and experimental data with different excitation frequencies

4 结论

本文针对油气悬挂系统中囊式蓄能器特性展开研究，对蓄能器的阻尼和刚度特性及影响因素进行了试验研究，并取得以下成果：

1）通过囊式蓄能器的试验研究发现，蓄能器内气体压力变化滞后于体积变化，证明迟滞时间是决定迟滞环开度的主要影响因素；

2）通过分析无迟滞时间的真实气体多变过程发现，蓄能器的刚度受激振频率的影响，随着激振频率增加，蓄能器的刚度不断减小；

3）提出了一种基于迟滞时间的真实气体多变过程指数的模型，该模型在研究范围内具有较高的精度。

本文研究结果对真实气体多变指数方程的完善具有一定指导价值，并为进一步正确的建立油气悬挂系统的模型奠定了基础。针对其他影响蓄能器性能的因素，如温度、气体压力等，尚需进一步试验验证。