图的电阻距离综述

杨玉军

（烟台大学数学与信息科学学院，山东 烟台264005）

0 引言

图的电阻距离来源于电网络中的等效电阻。给定一个连通图G＝（V（G），E（G）），如果将G中的每条边都看作是一个电阻（通常看作单位电阻），则G就可以看作一个（纯电阻）电网络N。G中任意两点i和j之间的电阻距离［1］，记作ΩG（i，j），定义为N中这两个节点之间的等效电阻，即单位电流从其中一个节点流入，从另一个节点流出时这两点间所产生的电势差。

图上最常用到的距离函数是（最短路）距离，其中顶点i和j之间的距离dG（i，j）定义为连接这两点的最短路的长度。与距离相比，电阻距离在反映图的整体性质方面更有优势，这是因为两点之间的距离只跟连接这两点的最短路的长度有关，而电阻距离不仅跟连接这两点的路的长度有关，也跟连接这两点的路的数目有关。在保持两点之间距离不变的情况下，如果增加一条连接这两点的路，则这两点之间的电阻距离会严格减小。

电阻距离的研究在物理、工程、数学、化学、生态学等众多学科领域都受到重视。电阻距离作为电路理论的重要组成部分，从文献［2］的经典结果开始就得到了众多物理和工程学者的研究，特别是它的计算问题一直是物理和工程中的经典研究问题。在数学领域，1993 年，Klein 等［1］明确指出，等效电阻是图上的距离函数，并将其命名为电阻距离，从此，电阻距离就成为图论领域的一个重要研究对象。更加有意义的是，电阻距离虽然纯粹是物理学概念，但是可以从代数、概率和组合等多个角度给出其等价的数学诠释，因此，它也得到了很多数学工作者的关注。在化学领域，电阻距离不仅比传统距离更适合于描述原子间的波状相互作用，更重要的是，基于电阻距离定义的化学分子拓扑指标，如Kirchhoff 指标、degree-Kirchhoff 指标、hyper-Kirchhoff 指标等，在定量构效关系（quantitative structure activity relationship，QSAR）和定量构性关系（quantitative structure properties relationship，QSPR）的研究中发挥着重要的作用。在生态学上，电阻距离常被用来构建生态学模型。

本文综述了电阻距离的计算公式、电阻距离的性质、电阻距离的和法则、电阻距离的递推公式以及若干重要图类的电阻距离解析计算公式，并给出了电阻距离研究领域的一个公开问题和两个猜想，为电阻距离的理论研究提供一定的理论参考。

1 电阻距离的计算公式

电阻距离虽然是来源于电路理论的物理概念，但是却有着纯粹的数学诠释，这可以从代数、概率和组合等多个角度给出其等价定义，这些等价定义也是电阻距离的数学计算公式。借助这些公式，就可以完全从数学的角度来计算图中的电阻距离。

1.1 代数公式

从代数的角度计算图的电阻距离，主要是利用图的Laplacian 矩阵来计算。通过Laplacian 矩阵的子矩阵，或者该矩阵的广义逆矩阵，又或者该矩阵的特征值和特征向量来计算。为了给出Laplacian矩阵的定义，首先介绍图的邻接矩阵的概念。

定义1设G是连通图，则G的邻接矩阵A（G）定义为A（G）＝（aij）n×n，其中

设D（G）＝diag（d1，d2，…，dn）是由G的顶点的度组成的对角阵，其中di表示G中顶点i的度，则有定义2。

定义2图G的Laplacian 矩阵L（G）定义为L（G）＝D（G）-A（G）。

由于Laplacian 矩阵的行和都等于零，所以Laplacian 矩阵的行列式等于零。但是，Laplacian 矩阵中任何一个元素的代数余子式均不为零，且都相等。令L（i）表示将Laplacian 矩阵的第i行和第i列删去后所得到的子矩阵，令L（i，j）表示将Laplacian 矩阵的第i、j行和第i、j列同时删去后所得到的子矩阵，则电阻距离有如下定理1 的计算公式。

定理1［3-6］设G为顶点数为n（n≥3）的连通图，则G中任意两点i和j之间的电阻距离为：

电阻距离也可以根据Laplacian 矩阵的广义逆矩阵来计算。为此，下面给出矩阵的广义逆矩阵的定义。

定义3设M是一个n×m阶实矩阵，如果m×n阶实矩阵H满足MHM＝M，则称H为M的广义逆矩阵，简称广义逆。特别地，如果M的广义逆H还满足HMH＝H、（MH）T＝MH、（HM）T＝HM，则称H为M的Moore-Penrose 逆。

根据广义逆理论，任何一个矩阵的广义逆都存在且不一定唯一，而Moore-Penrose 逆是存在且唯一的［7］。设H＝（hij）n×n是L（G）一个广义逆矩阵，则有如下定理2 的计算公式。

定理2［1，8-9］G中任意两点i和j之间的电阻距离为

特别地，如果H是对称矩阵，则有

为方便起见，计算时一般选取Laplacian 矩阵的Moore-Penrose 逆，记为L†（G）。容易验证，L†（G）＝（L（G）＋J／n）-1-J／n，其中J为n阶全1 矩阵。

利用上面的计算公式，就可以推导出用Laplacian 矩阵的特征值和特征向量来表示的电阻距离计算公式。为方便起见，设λ0≤λ1≤…≤λn-1是G的Laplacian 矩阵L（G）的特征值，称为G的Laplacian 特征值。由于L（G）是半正定矩阵，因此L（G）的所有特征值均大于或等于零。众所周知，G连通当且仅当λ0＝0 且对k＞0、λk＞0［10］。设U0，U1，…，Un-1是对应于λ0，λ1，…，λn-1的两两正交的单位特征向量，并且假设Uk＝。

定理3［11-13］设G是顶点数为n的连通图，则G中任意两点i和j之间的电阻距离为

除了Laplacian 矩阵，电阻距离也可以利用归一化Laplacian 矩阵来计算。下面首先给出该矩阵的定义。

定义4图G的归一化Laplacian 矩阵L（G）定义为：L（G）＝D（G）-1／2L（G）D（G）-1／2。

设φ0≤φ1≤…≤φn-1是L 的特征值，称为G的归一化Laplacian 特征值，则有φ0＝0，并且对k＞0，φk＞0［14］。设Φ0，Φ1，…，Φn-1是对应于φ0，φ1，…，φn-1的两两正交的单位特征向量，并且Φk＝，k＝0，1，…，n-1。

定理4［15］设G是顶点数为n的连通图，则G中任意两点i和j之间的电阻距离为

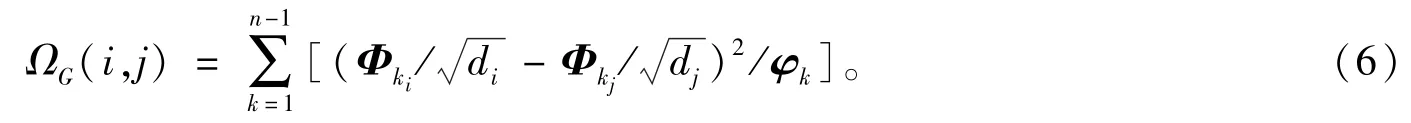
1.2 概率公式

概率公式主要是利用图上随机游走来计算电阻距离。设图G是顶点数为n的连通图，令pij＝则图G上的简单随机游走定义如下。

定义5一个质点在图G上的简单随机游走是一随机序列：X0，X1，…，Xn，…，这里Xn表示质点在n时刻的位置，若质点在n时刻位于顶点i，则下一时刻它位于顶点j的概率是pij。

令P（i→j）表示质点从i出发，在回到i之前到达j的概率，也称作逃逸概率，则电阻距离可以由逃逸概率通过下面的定理5 来计算。

定理5［16］G中任意两点i和j之间的电阻距离为

接下来，考虑图上随机游走的2 个重要参数：一个是质点从i出发首次到达j所需步数的期望值，称作从i到j的平均首达时间，记作H（i，j）；另一个是从i到j的平均往返时间，记作C（i，j），定义为质点从i出发到达j再返回i所需步数的期望值，即C（i，j）＝H（i，j）＋H（j，i）。有意思的是，两点之间的电阻距离和这两点之间的平均往返时间之间仅仅相差一个常数倍。

定理6［17］G中任意两点i和j之间的电阻距离为

1.3 组合公式

事实上，也可以用组合的方法来计算电阻距离。为此，首先介绍生成森林的概念。

定义6图G的一个k-生成森林F定义为图G的一个子图，它是k棵树的不交并且包含G的所有顶点。若k＝1，则称F为G的生成树。

图的生成森林的数目和图的Laplacian 矩阵和之间具有深刻的联系。著名的矩阵-树定理就建立了图的生成树的数目和Laplacian 矩阵的余子式之间的关系。

定理7［2］L（G）中任一元素的代数余子式就等于G的支撑树的数目τ（G）。也就是说，对每个i，都有detL（i）＝τ（G）。

对于图G的2-生成森林，也有类似的结论。设F是G的一个2-生成森林，如果顶点i和j分别位于F的两个不同的连通分支中，则称F分离i和j。记G中分离i和j的2-生成森林的数目为τG（i，j），则有定理8。

定理8［5，18］对于i≠j，detL（i，j）就等于G的分离i、j两点的2-支撑森林的数目，即detL（i，j）＝τG（i，j）。

将定理7 和定理8 中的结果代入定理1，就可以得到计算电阻距离的组合公式。

定理9［5］

最后，需要特别说明的是，本节所介绍的电阻距离的计算公式都是在非赋权图上考虑的，即每条边上的权值都是1。实际上，这些结果都可以推广到赋权图上，在此不一一给出。

2 电阻距离的性质

本节介绍关于电阻距离的一些性质，既包括作为距离所满足的一些数学性质，也包括作为等效电阻所满足的电路理论中的一些基本原理。本节所介绍的内容大多是在赋权图上讨论的，边上的权值代表边的电导（电阻的倒数）。显然，非赋权图可以看作赋权图的特殊情形。

作为图上的距离函数（或内在度量），电阻距离自然满足度量的性质。

性质1设ΩG（x，y）是图G上的电阻距离函数，则ΩG（x，y）满足：1）非负性，即对x，y∈V（G），ΩG（x，y）≥0，等号成立当且仅当x＝y；2）对称性，对x，y∈V（G），ΩG（x，y）＝ΩG（y，x）；3）三角不等式，对x，y，z∈V（G），ΩG（x，y）≤ΩG（x，z）＋ΩG（z，y）。

电阻距离还满足一个重要的数学性质，它是关于边上权值的凸函数。

性质2［19］（凸函数性质）设G1和G2是两个具有相同的顶点集和边集的图，边e上的权值分别为。对任意θ∈［0，1］，设Gθ是具有相同顶点集和边集的图，并且Gθ中边e上的权值满足，则对任意两点u，v，

注意到上面性质里图中边上的权值是这条边的电导，如果边上的权值换作电阻的话，则电阻距离就变成了关于边上权值的凹函数，该结论早在1956 年就被Shannon 等［20］得到。

接下来讨论电阻距离的割点性质。若连通图G中的一个点x满足G-x不连通，则称x是图G的一个割点。如果两个点位于G-x的不同分支中，那么连接这两点的所有的路都要经过x，此时这两点之间的电阻距离可以表示为这两点到割点的电阻距离之和，这个性质就是电阻距离所满足的割点性质。

性质3［1］（割点性质）设x是图G的一个割点，a和b分别位于G-x的不同连通分支中，则有

为了计算和估计电阻距离，经常会对电网络进行简化或者进行一些等效变换。首先介绍最常用到的众所周知的基本法则——串联法则和并联法则，这两个法则可以由基尔霍夫定律直接得到。

性质41）设P是一条路，a、b是P的两个端点，那么a、b之间的电阻距离等于P中所有边上的电阻之和（串联法则）；2）设G是由两个点a、b以及连接这两点的s条独立路所构成的图，假设这s条独立路上的边的电阻之和分别是r1，r2，…，rs，则有1／ΩG（a，b）＝1／r1＋1／r2＋…＋1／rs（并联法则）。

除了串并联法则，在电路理论中，星形联结与三角形联结的等效变换（Y-Δ变换）也是一个经常用到的基本变换。

性质5［21］（Y-Δ 变换）设三角形联结的3 个顶点是u1，u2，u3，3 条边u1u2，u1u3和u2u3上的电阻值分别是R12、R13和R23；再设星形联结的中心点是u，其余3 个顶点是u1、u2、u3，3 条边u1u、u2u和u3u上的电阻值分别是r1、r2和r3，则有：1）星形联结可以通过R12＝（r1r2＋r1r3＋r2r3）／r3、R13＝（r1r2＋r1r3＋r2r3）／r2、R23＝（r1r2＋r1r3＋r2r3）／r1转换为三角形联结；2）三角形联结可以通过r1＝R12R13／（R12＋R13＋R23）、r2＝R12R23／（R12＋R13＋R23）、r3＝R13R23／（R12＋R13＋R23）转换为星形联结。

接下来介绍电阻距离的消去法则。图G的一个不含割点的极大连通子图称作一个块。如果G的一个块恰好包含G的一个割点，那么就可以给出下面的法则。

性质6［22］（消去法则）设B是连通图G的块，且B恰包含图G的的一个割点x。设G′是G中将B-x的所有顶点删掉后所得到的图，则对G′中的任意两个顶点u、v，

下面再来介绍一个非常有用的变换——替代原理。在给出该原理之前，先介绍S-等价的概念。设图G和H的顶点集分别为V（G）和V（H），称G和H是S-等价的。如果对任意的u，v∈S，都有ΩG（u，v）＝ΩH（u，v），其中S⊆V（G）∩V（H）。显然，前面介绍的星形联结与三角形联结就是｛u1，u2，u3｝-等价的。类似于星形联结与三角形联结的等效变换，在计算电阻距离的时候，可以将图中的子图用等价的图进行替代。

性质7（替代原理）设H是G的一个子图，且H与H*是V（H）-等价的，那么将G中的H替代成H*得到的图G*满足ΩG（u，v）＝ΩG*（u，v），其中u，v∈V（G），即G与G*是V（G）-等价的。

以上都是在网络拓扑结构方面对网络进行等效变换和化简，下面考虑从代数的角度对网络进行简化，也称作网络的Kron 简化［23］。为此，将图G的顶点划分为两个集合V1和V2，V1中的顶点称作边界点，V2中的顶点称做内点，目的是通过网络的简化来计算边界点之间的电阻距离。根据顶点划分，图G的Laplacian 矩阵就可以写成如下的分块矩阵：L（G）＝。令L′＝L11-，则L′也可以看作某个图G′的Laplacian 矩阵。显然，G′的顶点集合是V1，是一个规模比G更小的网络。文献［23］就得到了如下的性质8。

性质8［23］（Kron 简化）设G是连通图，G′是以L′作为Laplacian 矩阵的图，则对G的任意两个边界点u，v∈V1，有

通过对原来的网络进行Kron 简化，将原有的网络转化为一个规模更小的网络，因此计算的复杂度明显降低。

除了电阻距离的精确计算，电阻距离的界的估计也是一个具有重要意义的研究问题。众所周知，电路理论中著名的Rayleigh 单调性法则，就是对电阻距离进行界的估计的一个基本法则。

性质9［16］（Rayleigh 单调性法则）如果G中某条边上的电阻值增加，则G中任意两点之间的电阻距离只增不减；反之，如果G中某条边上的电阻值减小，则G中任意两点之间的电阻距离只减不增。

作为Rayleigh 单调性法则的推论，可以容易得到Rayleigh 短切方法。确切来说，如果将G中的某条边删掉，相当于将该条边上的电阻值增加为无穷大，因此由Rayleigh 单调性法则可知，所删边后图中任意两点之间的电阻距离都不小于之前这两点之间的电阻距离；而如果将G中两个点等同为一个点，相当于将这两个点用电阻值为零的导线短路相接，也就是将连接这两点的边上的电阻值降为零，由Rayleigh 单调性法则可知，短接后任意两点之间的电阻距离不大于之前这两点之间的电阻距离。因此，在估计电阻距离时的一个重要技巧就是对原图进行删边或者短接操作，将原图转化为结构更为简单或者规模更小的图，进而通过所得到新图的电阻距离给出原图电阻距离的上界或者下界。比如，对连通图G中的任意两个顶点u、v，取连接这两点的一条最短路P，在G中将不在P上的边全部删掉，所得的图称为G′。显然，G′中u、v之间的电阻距离ΩG′（u，v）就等于它们在G中的距离dG（u，v），由Rayleigh 短切方法可知，ΩG（u，v）≤ΩG′（u，v）＝dG（u，v）。这就表明两点之间的距离是它们之间的电阻距离的一个上界。因此，显然有下面的性质10。

性质10［1］设G是连通图，则对G中任意两个顶点u和v，有

等号成立当且仅当u和v之间仅有唯一的一条路相连。

借助于Rayleigh 单调性法则，文献［24］给出了由顶点的度表示的电阻距离的下界。

性质11［24］设G是简单连通图，则任意两点u、v之间的电阻距离满足

等式成立当且仅当u、v相邻并且在G-｛u，v｝中有相同的邻集，其中du表示G中顶点u的度。

本节的最后给出一个图及其对偶图的电阻距离之间的一个有趣的关系式。这里考虑的图是非赋权图，即图中每条边上的电阻值都是1。设G是2-边连通图，则图G*称作图G的对偶图，如果存在一个双射φ：E（G）→E（G*），满足G的边子集E是G的一个圈当且仅当φ（E）是G*的一个极小边割。事实上，对于所考虑的有限图而言，Whiteny［25］的经典结果表明，如果G*是有限图G的对偶图，则G和G*都是平面图并且互为几何对偶。这里，平面图的几何对偶定义如下：设G是平面图，在平面图G的每个面内选取一点作为顶点，对于G的任一条边，将与其相邻的两个面内的顶点用一条仅与有一交点且不与图G的其他任何边相交的简单曲线连结，这样得到的平面图称为G的几何对偶，记作G*。容易看出，上述几何对偶的定义给出了G和G*的边之间的一一对应，G中的边e和G*中的对应边G*就成为一对对偶边。

Thomassen 建立了如下的关于一个图及其对偶图的电阻距离之间的关系。

性质12［26］设G是平面图，G*是G的对偶图，e＝uv和e*＝u*v*互为对偶边，则有

3 电阻距离的和法则

图中所有顶点或者部分顶点之间的电阻距离之和满足一些非常简洁漂亮的等式关系，也称这些等式关系为电阻距离的和法则。本节将综述电阻距离所满足的一些和法则。需要说明的是，本节所考虑的是非赋权图的情形，尽管很多结果都可以推广到赋权图上。为简便起见，在不产生歧义的前提下，一般将ΩG（i，j）简写为Ω（i，j）。

在电阻距离的和法则中，早在1949 年，Foster 就建立了一个著名的法则，称作Foster 第一公式。

定理10［27］（Foster 第一公式）设G是顶点数为n的连通图，则有

和号取遍所有的相邻的点对。

如此简洁美妙的结果引起了众多学者的兴趣，该公式后来被多位学者从不同的角度给出了证明，特别是文献［28］就从组合的角度给出了该公式的证明。

1961 年，Foster 又得到了一个新的和法则，称为Foster 第二公式。

定理11［29］（Foster 第二公式）设G是顶点数为n的连通图，则有

和号取遍所有的相邻边ik和kj。

后来，多位学者又进一步将上述结果推广到了所谓的Foster 第k公式。

定理12［30-32］（Foster 第k公式）设G是顶点数为n的连通图，则有

其中：Pk表示图上随机游走的状态转移矩阵P＝D（G）-1A（G）的k次幂；tr 表示矩阵的迹。

2002 年，Klein 巧妙地建立了以矩阵元素赋权的所有顶点的电阻距离之和的等式关系，为后续一系列电阻距离和法则的建立奠定了基础。

定理13［30］对顶点数为n的图G以及任意的n×n的矩阵M，

由于定理13 中的矩阵M是任意矩阵，因此通过将M取作一些特殊矩阵，就可以得到一些有趣的关系式。容易验证，如果令M＝L†，就可以得到Foster 第一公式。如果令M＝（L†）2，就可以得到图中所有顶点对之间的电阻距离之和的一个重要的计算公式。

定理14［33］设G是顶点数为n的连通图，则有

定理14 中等号的左侧就是著名的分子结构拓扑指标——Kirchhoff 指标，因此该定理建立了Kirchhoff 指标与Laplacian 特征值之间的一个非常优美的关系式。类似地，文献［34］也建立了度乘积Kirchhoff 指标与归一化Laplacian 矩阵的特征值之间的一个优美的关系式，即定理15。

定理15［34］设G是顶点数为n、边数为m的连通图，则有

在定理13 中取矩阵M为除位于第i行第j列的那个元素为1 以外其余元素为0 的矩阵，Klein 得到了下面的和法则。

定理16［30］在连通图G中，令i，j∈V（G），则

其中：n（i）表示顶点i的邻集；如果i和j相邻，δi～j则取值为1，否则为0。

在定理13 的基础上，文献［34］通过选取恰当的矩阵M，建立了新的电阻距离（局部）和法则，主要结果如定理17。

定理17设G是顶点数为n的连通图，则：1）对任意的i，j∈V（i≠j），有

2）对任意3 个不同的顶点i，j，k∈V，有

后续研究表明，定理17 在电阻距离的计算中具有非常重要的应用，特别是在计算一些特殊图类以及图运算的电阻距离时非常有效。

类似于Klein 在2002 年得到的定理13 的结果，文献［35］得到了定理18 和定理19。

定理18［35］对顶点数为n的图G和每一列的元素之和都为0 的任意n×n矩阵M，有

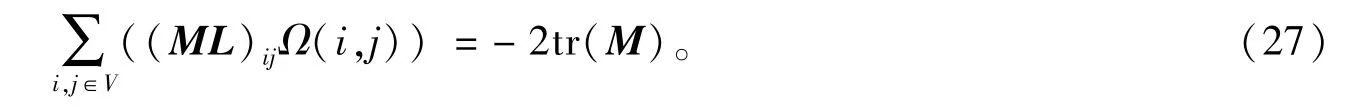
定理19［35］对顶点数为n的图G和每一行的元素之和都为0 的任意n×n矩阵M，有

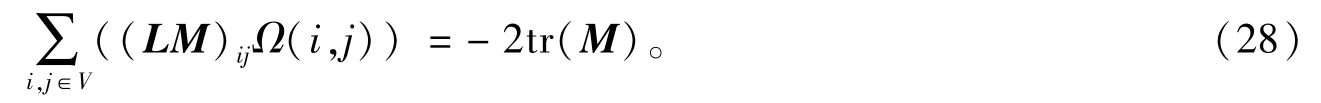
通过将定理18 和定理19 中的M取作特殊矩阵，得到了下面的定理20～定理22。

定理20［35］设i，j是图G的顶点，则

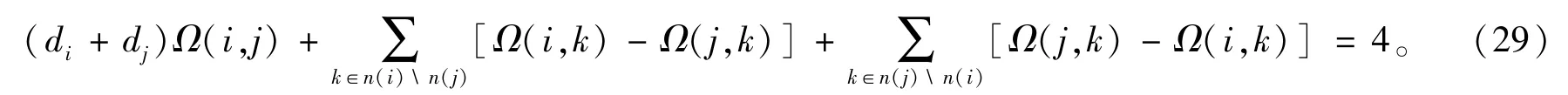
定理21［35］设i，j，k是图G的顶点，则

定理22［35］设i，j，k，l是G的顶点，则

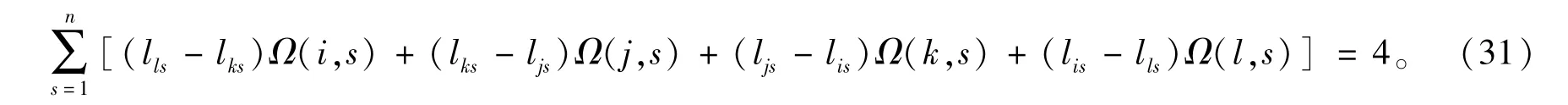
需要指出的是，利用定理20～定理22 中的结果，文献［35］得到：对顶点集合的大小为2、3或4 的子集S，如果S中的顶点在G-S中有相同的邻集N，那么S中任意两点的电阻距离就可以根据N的大小给出。换句话说，它们可以被子图G［S］和N的大小唯一确定。一个自然的问题就是，当S中的顶点数大于4 时，结果还是否成立？文献［35］证明了该性质对顶点数任意多的S都是成立的，从而给出了下面的简化原理。

性质13（简化原理）如果S⊂V（G）满足S中的所有顶点在G-S中有相同的邻集N，则S中任意两点之间的电阻距离就等于在G［S∪N］中删除所有连接N中顶点之间的边后所得子图中这两点之间的电阻距离。

4 电阻距离的一个递推公式

本节主要介绍计算电阻距离的一个重要的方法——递推公式。在计算电阻距离的时候，一个自然的想法就是在图中删掉一条边后，能否利用删边后的子图的电阻距离来计算原图的电阻距离。如果能够实现的话，那么就可以对原图逐步删边，从而使得电阻距离的计算变得更加容易。文献［36］就考虑并解决了这一问题。并且，该文考虑了更一般的情形，就是给赋权图上某条边的权值一个变化量，考虑变化后的图和原图的电阻距离之间的关系。

利用发生扰动后矩阵的逆矩阵的变化情况，文献［36］就得到了赋权图G的某条边上的权值发生变化后电阻距离的变化情况。

定理23［36］（赋权图的电阻距离递推公式）设Ω和Ω′分别是赋权图G和G′上的电阻距离函数，G和G′具有相同的顶点集和边集，并且除了边e＝ij上的权值分别是w和w′之外，其余边上的权值都完全相同，则对p，q∈V（G）＝V（G′），有

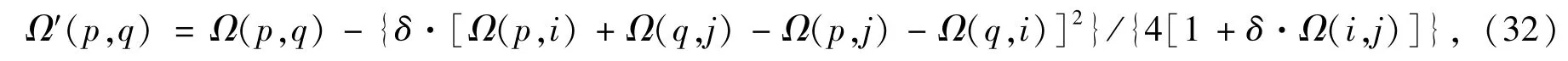
其中δ＝w′-w。

对于非赋权图的情形，由于删边相当于将边上的权值（电导）由1 变为0，加边相当于将边上的权值由0 变为1，因此由定理23 容易得到定理24。

定理24［36］（非赋权图的电阻距离递推公式）若G＝G′＋ij，则有

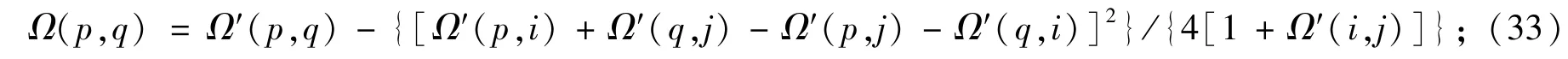
若G＝G′-ij，则有

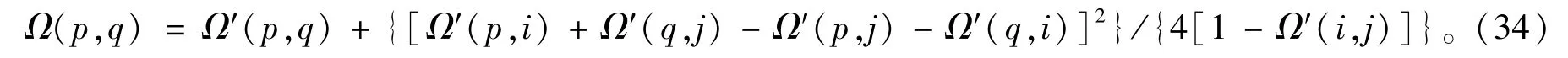
根据电阻距离的递推公式，容易推导出Rayleigh 单调性法则中的结论。并且，Rayleigh 单调性法则只是给出了电阻距离变化情况的定性描述，而电阻距离的递推公式还给出了图中某条边上的电阻值发生变化后，图中任意两点的电阻距离变化情况的精确的定量描述。并且，文献［36］还进一步得到，如果边e＝ij上的权值发生变化，那么G中i和j之间的电阻距离的变化量最大。事实表明，电阻距离递推公式在计算一些特殊图的电阻距离时非常有效。

接下来，根据电阻距离递推公式进一步考虑将G中的两个点i和j短接（将两个点等同为一个点）后电阻距离的变化情况。

定理25［36］设G*是将i和j等同为一个点后所得到的图，则有

由定理23 和定理25 就可以得到关于G、G′和G*的电阻距离之间的一个有趣的关系式。

定理26［36］设G、G′和G*定义如上，则有Ω（p，q）＝［1＋δ·Ω（i，j）］Ω′（p，q）-δ·Ω（i，j）Ω*（p，q）。

特别地，如果考虑非赋权图的情形，对e∈E（G），设G′＝G-e，G*＝G／e，其中G／e表示在G中收缩边e，则由定理26 可以得到下面的删边-收缩定理。

定理27［36］设G是非赋权图且e是G的一条边，令G′＝G-e，G*＝G／e，则有：Ω（p，q）＝［1-Ω（i，j）］Ω′（p，q）＋Ω（i，j）Ω*（p，q）。

设C是连通图G的边集合的一个子集合，若G-C不连通，则称C为G的一个边割集。进一步，如果＝k，则称C是一个k-边割集。电阻距离的递推公式另一个重要应用就是，如果图G包含极小的2-边割集或者3-边割集，那么，G中的电阻距离就可以由删掉边割后所得到的子图的电阻距离来计算。

定理28［36］设G是连通图，C是G的一个极小2-边割集，G1和G2是G-C的两个连通分支。若p和q属于G1∪G2的同一个连通分支，不妨设为G1，则有

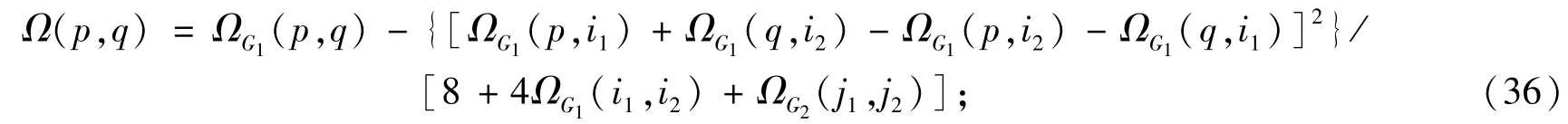
若p∈G1且q∈G2，则有：

对于3-边割集的情形，有类似的结果。

定理29［36］设G是连通图，C是G的一个极小3-边割集，G1和G2是G-C的两个连通分支。若p和q属于G1∪G2的同一个连通分支，不妨设为G1，则有

若p∈G1且q∈G2，则有

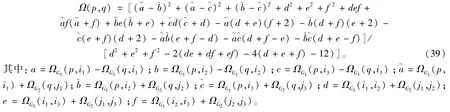
5 若干重要图类的电阻距离解析计算公式

电阻距离的计算问题一直是物理和工程中的一个经典问题。近年来，学者得到了若干图类和电网络的电阻距离的解析计算公式，本节仅列举部分重要图类的计算结果。由于篇幅限制，个别复杂记号没有给出，解释说明参见所引文献。在不产生歧义的情况下，将ΩG（i，j）简记为Ω（i，j）。

定理30［37］圈Cn中的i和j之间的电阻距离为

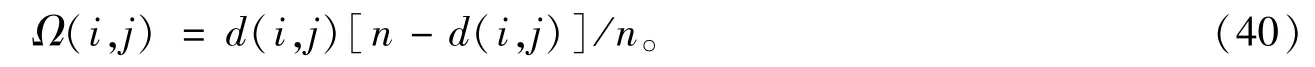
定理31［38］完全图Kn中的i和j之间的电阻距离为

定理32［39］直径为D（G）的距离传递图G中距离为t（1≤t≤D（G））的任意两点i与j之间的电阻距离为

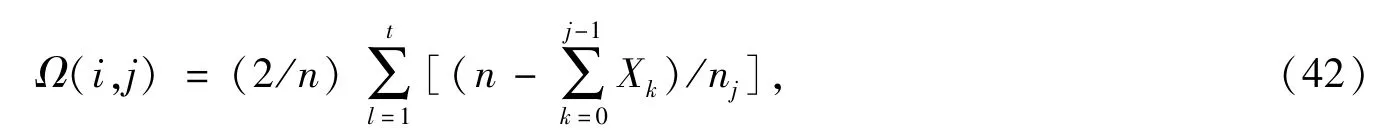
这里Xk＝b0b1b2…bk／（c1c2…ck），nk＝Xkck，其中bi指任取G中的一个顶点对G进行距离分层后，第i层的任一顶点在第i＋1 层的邻点的个数（0≤i≤D（G）-1），而ci指第i层的任一顶点在第i-1 层的邻点的个数（0≤i≤D（G））。

定理33［40］完全二部图Km，n（二部划分为X，Y且）中的i和j之间的电阻距离为：1）若i，j∈X（或i，j∈Y），则Ω（i，j）＝2／n（或Ω（i，j）＝2／m）；2）若i∈X，j∈Y，则Ω（i，j）＝（m＋n-1）／（mn）。

2003 年，文献［41］得到了循环图的电阻距离计算公式，即定理34。

定理34［41］设循环图G的Laplacian 矩阵为L（G）＝C［l0，l1，l2，…，ln-1］，则对i，j∈V（G），

2010 年，文献［42］给出了轮图和扇图的电阻距离解析计算公式，即定理35。

定理36［42］设n≥1 为正整数，则扇图Fn的任意两点间的电阻距离为：1）点n＋1（扇图的中心点）和点i∈｛1，2，…，n｝之间的电阻距离为F2（n-i）＋1F2i-1／F2n；2）若点i，j∈｛1，2，…，n｝且i＜j，则点i，j之间的电阻距离为［F2（n-j）＋1（F2j-1-F2i-1）＋F2i-1（F2（n-i）＋1-F2（n-j）＋1）］／F2n，其中Fk是第k个斐波那契数。

2011 年，文献［43］得到了凯莱图的电阻距离计算公式。

将两条n个顶点的路Pn＝p1p2…pn、＝q1q2…qn中的所有对应顶点pi和qi（1≤i≤n）连边后所得到的图称作梯子图，记作Ln。文献［45-46］利用不同的方法，分别独立得到了梯子图的电阻距离解析计算公式。

定理39［45-46］Ln中任意两点间的电阻距离为：Ω（pi，pj）＝Ω（qi，qj）＝（i-j）／2＋（1-αi-j）（2-αi＋j-1＋α2j-1＋α2n-2i＋1（1-αi-j-2αi＋j-1））／；Ω（qi，pj）＝Ω（pi，qj）＝（i-j）／2＋（1＋αi-j）（2＋αi＋j-1＋α2j-1＋α2n-2i＋1（1＋αi-j＋2αi＋j-1））／，其中α＝2-。

2017 年，文献［47］定义了一类环形网络并得到了这类网络的电阻距离计算公式。

定理40［47］设G［mk］为环形网络，其点集为V＝V1∪V2∪…∪Vn，且m1，m2，…，mn为正整数（n≥3），＝mi，Vn＋1＝V1，ρi＝，1≤i≤n，mn＋1＝m1，则有：1）若a，b∈V1，则Ω（a，b）＝2／（mn＋m2）；2）若a∈V1，b∈Vi≠V1，则Ω（a，b）＝（ρi-1（ρn-ρi-1））／ρn＋（m1-1）／（m1（mn＋m2））＋（mi-1）／（mi（mi-1＋mi＋1））；3）若a，b∈Vi，则Ω（a，b）＝2／（mi-1＋mi＋1）；4）若a∈Vi，b∈Vj，i＜j，则Ω（a，b）＝（ρ′ij（ρn-ρ′ij））／ρn＋（mi-1）／（mi（mi-1＋mi＋1））＋（mj-1）／（mj（mj-1＋mj＋1））。其中，。

后来，文献［48］又定义了一类路网络，并得到了这类网络的电阻距离计算公式。

定理41［48］设P［mk］为路网络，其点集为V＝V1∪V2∪…∪Vn，且m1，m2，…，mn是n个正整数（n≥2），＝mi，Vn＋1＝V1，qij＝，1≤i≤n，mn＋1＝m1，则有：1）若a，b∈Vi，则Ω（a，b）＝2／（mi-1＋mi＋1）；2）若a∈Vi，b∈Vj，则Ω（a，b）＝（mi-1）／（mi（mi-1＋mi＋1））＋qij＋（mj-1）／（mj（mj-1＋mj＋1）。

2019 年，文献［49］确定了几乎完全二部图中顶点之间的电阻距离。

定理42［49］设G（n，p）＝Kn，n-pK2为几乎完全二部图，其中点集为V＝｛x1，x2，…，xn｝∪｛y1，y2，…，yn｝，边集为E＝≤i，j≤n｝＼｛x1y1，x2y2，…，xpyp｝，则G（n，p）＝：Kn，n-pK2的电阻距离为：

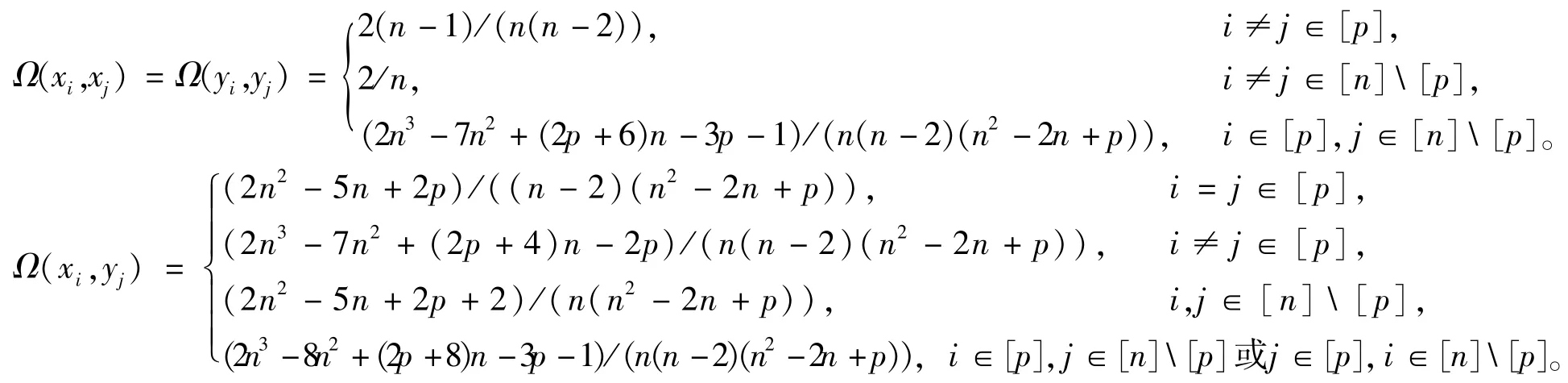
2020 年，文献［50］将文献［49］中的结果进一步推广到近似完全二部图。

定理43［50］设G（m，n，p）＝Km，n-pK2为通过完全二部图Km，n删除大小为p的匹配得到的图，则：

1）若1≤i，j≤m，有

2）若1≤i，j≤n，有

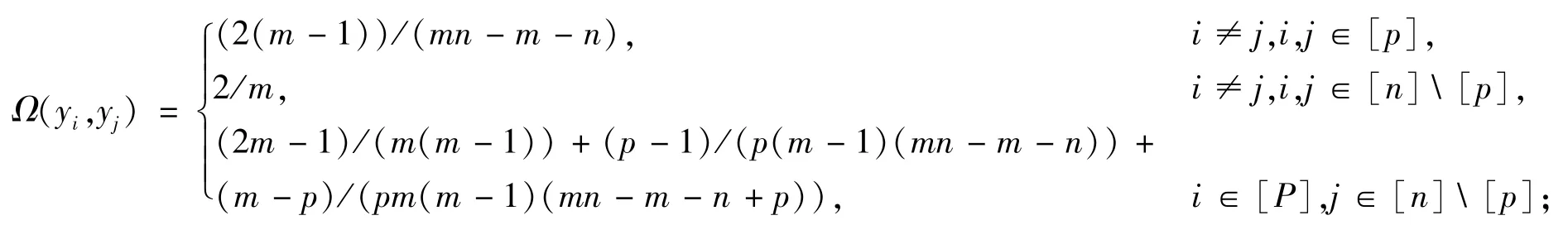
3）若1≤i≤m且1≤j≤n，有

2019 年，文献［51］得到了直线性2-树的电阻距离。

定理44［51］给定一个具有n个点、m＝n-2 个单元的直线性2-树，则对1≤j＜n，1≤k≤n-j，顶点j和j＋k之间的电阻距离为：Ω（j，j＋k）＝＋Fm＋1［Fm-k（kSk-Fk）＋Fm-k＋1（（k-5）Fk＋1＋（2k＋2）Fk）］／5｝／F2m＋2，其中：Fk为第k个斐波那契数；Sk为第k个卢卡斯数。

分形网络的电阻距离也是备受关注的研究热点，如阿波罗网络［52］、谢尔宾斯基垫圈网络［53］、自相似（x，y）-鲜花网络［54］等。2019 年，文献［55］就给出了灌封网络的电阻距离。为了方便起见，本定理中电阻距离的记号和原文保持一致，即用ruv（t）表示t次迭代后得到的灌封网络Nt顶点u和v之间的电阻距离。

定理45［55］设Nt＝（Gt，ω）为（m，n）-灌封网络，u、v是Nt中的两个不同的顶点，则有：

1）若u，v∈Vt-1，则ruv（t）＝2mruv（t-1）／（m＋2）；

2）若u∈Vt-1，v∈｛e0，e1，e2，…，en，e1，e2，…，em-1｝，其中e＝（a，b），则ruv（t）＝其中：η1＝1／2；η2＝3／2；η3＝j（m-j）／m；Θ1＝Θ2＝rua（t-1）＋rub（t-1）-rab（t-1）／2，Θ3＝（m-j）rua（t-1）＋jrub（t-1）-j（m-j）rab（t-1）／m；

3）若u，v∈｛e0，e1，e2，…，en，e1，e2，…，em-1｝∪｛f0，f1，f2，…，fn，f1，f2，…，fm-1｝，其中e＝（a，b），

其中：α1＝α4＝1；α2＝α5＝2；α6＝3；α3＝（m＋i-j）（j-i）／m；α7＝1／2＋i（m-i）／m；α8＝3／2＋j（m-j）／m；α9＝i（m-i）＋j（m-j）／m，β3＝（j-i）2rab（t-1）；β4＝β5＝β6＝rac（t-1）＋rad（t-1）＋rbc（t-1）＋rbd（t-1）-rab（t-1）-rcd（t-1）；β7＝（m-i）［rac（t-1）＋rad（t-1）］＋i［rbc（t-1）＋rbd（t-1）］-mrab（t-1）／2-2i（m-i）rcd（t-1）／m；β8＝（m-j）［rac（t-1）＋rbc（t-1）］＋j［rad（t-1）＋rbd（t-1）］-mrab（t-1）／2-2j（m-j）rcd（t-1）／m；β9＝（m-i）（m-j）rac（t-1）＋j（m-i）rad（t-1）＋i（m-j）rbc（t-1）＋ijrbd（t-1）-i（m-i）rab（t-1）-j（m-j）rcd（t-1）。

2020 年，文献［56］得到了线性六角链网络和环形六角链网络的电阻距离计算公式。

6 总结

由于自身的重要性以及在其他领域的广泛应用，电阻距离得到了来自数学、化学、物理、工程、生物学、社会学、网络科学等众多领域学者的广泛研究，产生了丰富的理论成果。本文仅仅综述了在电阻距离的计算和电阻距离的性质研究方面所取得的一些研究成果。在本文所介绍的成果之外，仍有关于电阻距离的大量的研究成果，比如近年来在图运算的电阻距离、图的Kirchhoff 指标等方面均取得了丰硕的研究成果。由于篇幅原因，本文不再列举。

电阻距离的研究尚有很多有意义的研究问题，本文最后列举2 个此方面的研究问题供读者参考。

1981 年，Godsil［57］提出了等树图的概念。如果一个图的所有边都包含在相同数目的生成树中，则称这样的图是等树图。从电阻距离的角度来看，等树图就是所有边的两个端点的电阻距离相等的图。周江等［58］从电阻距离的角度给出了等树图的刻画。但是，到目前为止，还没有关于哪些图是等树图的完整刻画。因此，本文提出如下的问题1，即：刻画哪些图是等树图？

在图的平均距离的研究中，有一个著名的猜想，称作4／3 猜想。该猜想具体为：设G是2-连通图，则存在一条边e，使得G-e的平均距离和G的平均距离的比值不超过4／3。对于平均电阻距离，猜想比值不超过2。因此，本文有如下的猜想。

猜想1设G是2-连通图，则存在一条边e，使得G-e的平均电阻距离和G的平均电阻距离的比值不超过2。

2020 年，Sardar 等［59］率先开展了电阻直径的研究。类似于图的直径，图G的电阻直径定义为G中所有顶点之间的电阻距离的最大值，记作Dr（G）。文献［60］证明了：如果G是树或单圈图，则G的线图的电阻直径小于等于G的电阻直径。借助于计算机，他们验证了对于顶点数不超过11 的图G，都有G的线图的电阻直径小于等于G的电阻直径成立。因此，他们猜想，该结果对于所有的图都成立。

猜想2对任意的连通图G，设LG是G的线图，则有Dr（LG）≤Dr（G）。