小型吊舱式无人艇航向控制

郑艳芳，俞万能，2，3，廖卫强，2，蒋仁炎

（1.集美大学轮机工程学院，福建 厦门361021；2.福建省船舶与海洋工程重点实验室，福建 厦门361021；3.船舶辅助导航技术国家地方联合工程研究中心，福建 厦门361021）

0 引言

无人艇具有体积小、速度快、隐蔽性强、控制灵活等特点，可执行海上救援、水质监测等任务，具有良好的应用前景［1］。而无人艇在航行过程中，控制系统存在非线性特点，再加上模型参数不确定、风浪等不可预测的外部扰动问题，导致角度偏航以及航行轨迹异常或失控等现象［2］。

为了解决上述航行问题，许多专家及学者对无人艇航向控制进行了研究［3］。Yu 等［4］针对船舶航向控制中模型参数不确定性问题，设计平方和分解（SOS）的非线性控制器，确保在不确定参数的情况下，对求证的不等式进行一定的恒等变换和放缩，但是SOS 求解存在互相关联的不等式约束，以及集合包含问题；张显库等［5］采用闭环增益成形算法设计非线性反推控制器，并在非线性反馈算法基础上提出一种新的正弦函数非线性修正算法，将正弦函数嵌入原控制器后，改进闭环增益成形算法的摄动问题，降低船舶输出能耗，但是存在延时问题，需要进一步优化；武颖等［6］采用指数滑模和反演相结合的方法设计航向控制器，通过反演算法的有效减弱抖振现象使系统全局渐近稳定，但是面对扰动具有一定的波动性；Piao 等［7］在系统初始阶段添加跟踪微分器，消除滑模抖振，根据基于逼近律和自适应反演的滑模控制，设计基于小脑模型关节控制器（CMAC）的最优控制器，实现吊舱驱动无人艇的运动控制，由于精度不高，面对扰动以及大量的计算存在时延性问题；靳海英等［6］通过分析吊舱式推进器特性进行建模，并采用滑模控制对吊舱式船舶进行航向控制，但是存在一定抖振现象，面对环境干扰因素容易出现局部不稳定情况。

那么针对航向控制系统存在外部扰动、模型参数不确定性以及时间延迟问题，本文以吊舱式无人艇为研究对象，采用RBF 神经网络结合迭代滑模算法设计航向控制器。迭代滑模算法主要是提高收敛速度和减弱干扰，而RBF 神经网络作为一种前馈神经网络，可进行全局逼近，改善局部最小，补偿模型参数不确定、外界扰动和减小滑模抖振问题。两者相结合可进一步减小扰动，优化滑模控制律和提高控制精度，保持吊舱式无人艇航向稳定性，适用于解决无人艇非线性系统运动控制问题。

1 吊舱式无人艇航向控制系统组成

吊舱式无人艇航向控制器结构图如图1 所示。主要包括吊舱无人艇运动数学模型、吊舱推进控制和航向控制器。通过分析吊舱式推进的性能，建立无人艇运动数学模型，并采用RBF 神经网络和迭代滑模控制算法设计航向控制器，最后输出对应的吊舱转向角进行航向偏差调节。

图1 吊舱式无人艇航向控制器结构图Fig.1 Structure diagram of course controller for pod-type USV

1.1 吊舱式无人艇运动数学模型

根据吊舱推进特性可知，吊舱推进具有良好的机动性和推进效率高等优点，而且吊舱式推进系统垂直贯穿于无人艇尾部主轴，可大幅度减小船舶内部空间［9］。根据燕聃聃等［10］对吊舱推进的研究，针对该吊舱式无人艇进行平面运动受力分析与建模。

由现有经验可知，船舶的垂荡、横摇和纵摇运动对船舶运动控制研究影响较小，因此本文只考虑前进、横漂和艏摇三自由度运动［11］。无人艇平面运动图如图2 所示。通过运动分析可知，无人艇在运动过程中主要受到推力及侧向力的作用，在偏航时通过改变转向角δ使得无人艇保持期望航向［12］。结合Piao 等［13］对船舶运动模型的研究，可得吊舱无人艇模型运动方程为

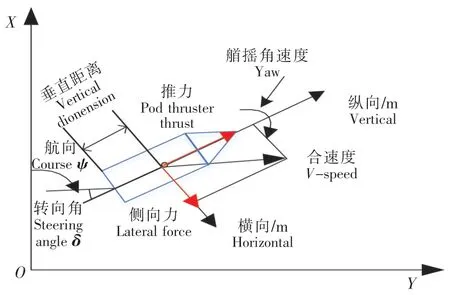
图2 无人艇的平面运动示意图Fig.2 Schematic diagram of the plane movement of the USV

式中：X、Y、N分别为无人艇纵向力、横向力以及艏摇力矩；H 表示船体；Pod 表示吊舱推进器；m为无人艇质量；mx，my为x轴、y轴方向的附加质量；u，v，r为无人艇运动中的前进速度、横漂速度和转首角速度；Izz为x轴的惯性矩；Jzz为z轴方向上的附加惯性矩；ψ为无人艇航向角。

1.2 吊舱式推进器矢量模型

根据赵雅聪［14］对吊舱推进器的研究，并结合无人艇特性，对公式（1）中的吊舱推进器进行矢量建模：

式中：XPod，YPod，NPod分别为吊舱推进纵向推力、侧向推力及回转力矩；tpod为螺旋桨推力减额系数；tR为转向阻力减额系数；Tp为吊舱推进器推力；Q为吊舱侧向力；δ为吊舱转向角；αHPod为吊舱诱导的侧向力系数；xHPod为吊舱-船体侧向力系数作用点的纵向坐标；xPod为吊舱压力中心的纵向坐标。

其中：Tp和Q的表达式为

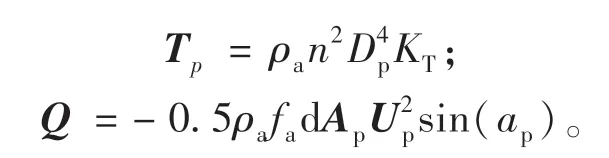
式中：ρa为海水密度；n为螺旋桨转速；Dp为螺旋桨直径；KT为螺旋桨推力系数；ap为吊舱有效攻角，取值范围为（-0.5236 rad，0.5236 rad），则在取值范围内sin（ap）≈ap≈δ；fa为冲角，ap＝0 时的斜率；Ap为吊舱有效面积；Up为吊舱有效来流速度。

联立吊舱式无人艇航向控制系统运动数学模型公式（1），在MATLAB／Simulink 仿真环境中建立小型吊舱无人艇航向控制仿真模型，如图3 所示。

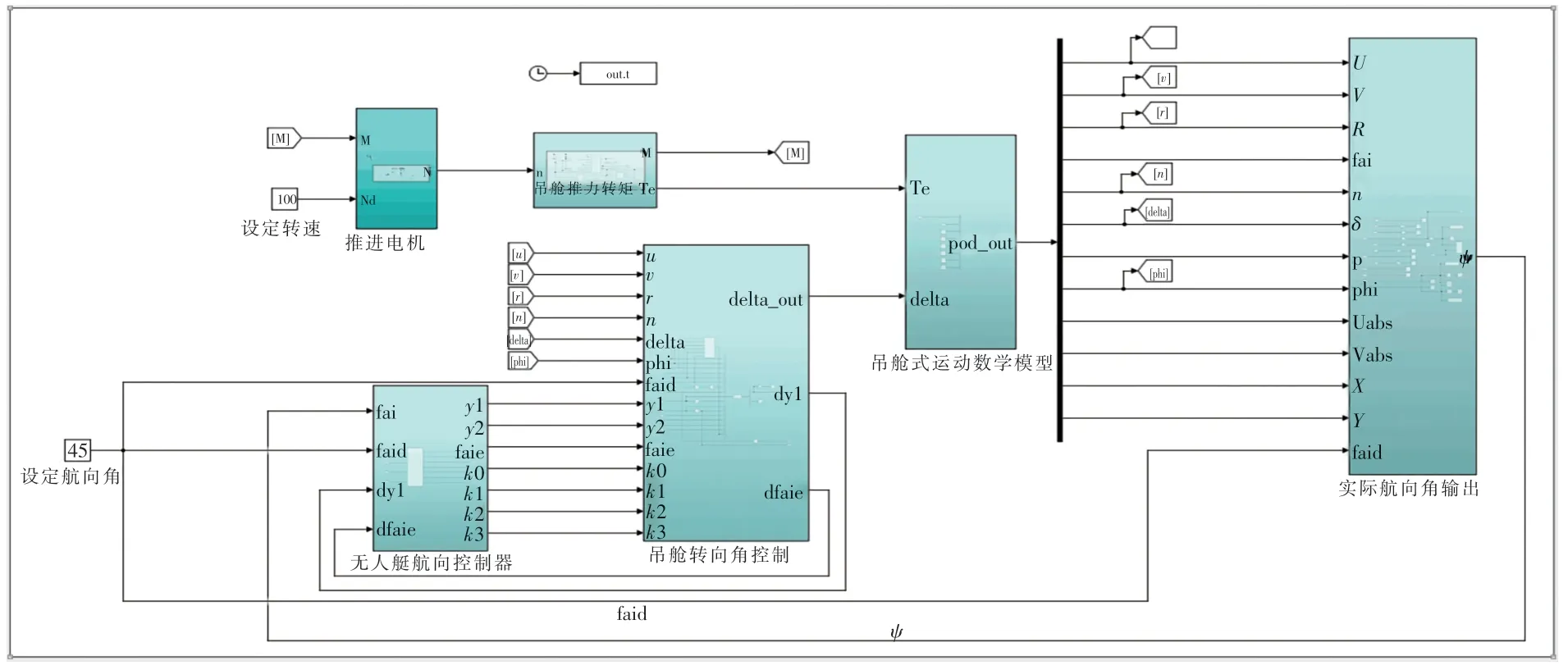
图3 小型吊舱无人艇航向控制仿真模型Fig.3 Simulation model of course control for pod-type USV

2 基于RBF 神经网络自适应迭代滑模的吊舱式无人艇航向控制器

吊舱式无人艇控制系统具有非线性和复杂性的特点，在风、浪干扰下，无人艇摆动明显，若无法及时校正航向偏差，将出现航行偏离甚至控制失效等现象［15］。采用RBF 神经网络自适应迭代滑模算法设计一种航向控制器，校正扰动和模型不确定性问题，提高收敛速度，满足无人艇航行精度要求。

2.1 迭代滑模航向控制设计

迭代滑模算法可克服系统的不确定，提高响应速度，所以采取迭代滑模算法使实际航向能够跟踪无人艇设定航向xd［16］。定义航向偏差e＝x1-xd，则偏差导数为，无人艇航向器设计目标是减小偏差，使得e、必须逐渐趋近于零，即保证系统沿“滑模切换面”运动。

迭代滑模算法运动性能只取决于滑动面控制参数［17］，设“滑模切换面”为sn＝＋ce，n＝1，2，…，c＞0。其中：c为“滑模切换面”控制参数。令＝-λsgn（sn），n＝1，2，…，λ＞0 为可调参数。设吊舱转向角δ＝uL，则吊舱转向角控制律为uL＝-［f（x，T）＋Dwr＋］／b，c＞0。式中：f（x，T）为流体动力项；T为时间常数；Dwr＝（Nwave＋Nwind）／（Izz＋Jzz）为风浪扰动项；b＝-［（xPod＋aHPodxHPod）（）＋xPod（1-tp）Tp］／（Izz＋Jzz）。

图4 滑模状态点运动过程示意图Fig.4 Schematic diagram of sliding mode state point movement process

根据无人艇吊舱转向角约束条件，引入饱和函数对其进行设计［18-19］，令饱和函数为非线性正切函数。由此可知：当x→0 时，其函数斜率比较大，随着x值逐渐增加，斜率e0逐渐减小并趋近于零，所以其饱和函数满足操纵运动中降低吊舱航向角偏差的要求，并保持稳定。

进一步构建航向偏差“滑模切换面”为

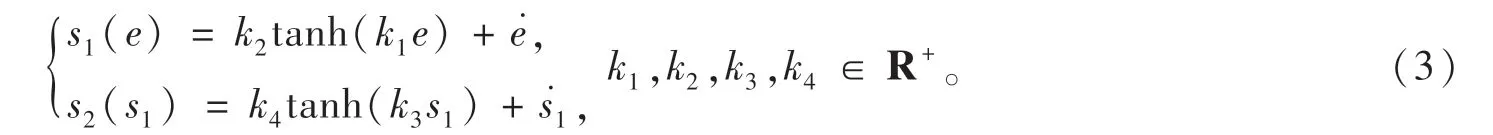
式中：k1，k2，k3，k4为可调参数；当s2→0 时，s1→0。为了满足系统有效到达“滑模切换面”，对s2进行镇定控制，保证s2收敛速度快于s1，保证参数k4≥k2。

展开公式（3）得

构建Lyapunov 函数

式中，η＞0，满足≤0，将公式（6）和公式（7）联立，可得系统稳定条件为：

当s2满足公式（8）时，系统渐近稳定，则得到满足稳定条件的吊舱转向角控制律为：

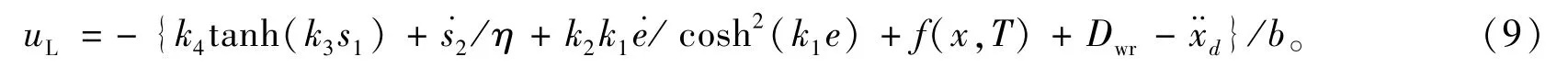
化简公式（9）得：

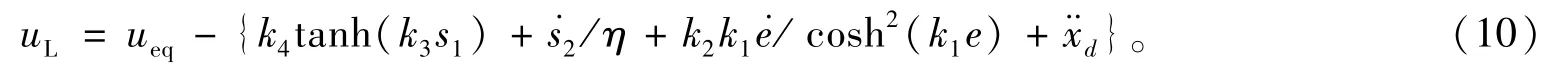
式中：ueq＝-（f（x，T）＋Dwr）／b。包含系统未知非线性函数f（x，T）和扰动Dwr，则为使ueq的值稳定，其“滑模切换面”s2→0，而吊舱转向角控制律uL为光滑有界函数，在短时间内变化很小，故引入uL（t-Δ）对ueq进行估计，Δ为估计值，随着t增大，满足Δ→0，则：

化简后得：

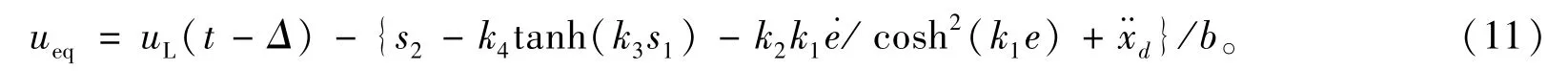
将公式（11）代入公式（10）得：

2.2 改进的自适应滑模航向控制设计

由于公式（4）中存在f（x，T）的不确定性项和风、浪扰动未知扰动Dwr。综合Han 等［20］研究，采用RBF 神经网络优化等效迭代滑模转向角控制律，进一步逼近非线性正切函数，减弱扰动Dwr误差影响，提高动态响应特性。

RBF 神经网络的高斯基函数输出为：

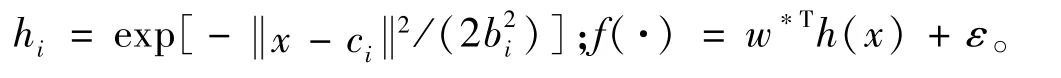
式中：i为网络隐含层第i个网络输入，i＝1，2，…，m m∈N＋；ci为高斯基函数中心位置；bi为基宽参数；ε为网络逼近误差；w*为理想网络权值，由于w*在实际中无法得到，故采取为理想网络权值估计值，设为估计误差，则理想网络权值估计值为：。

设神经网络输入为x＝［u v r ψ］T，则神经网络估计值输出为：。

将神经网络估计值代入公式（9）中得：

RBF 神经网络的理想网络权值向量自适应律及理想有界估计值为

将公式（14）、公式（15）和公式（16）代入公式（17）中化简得

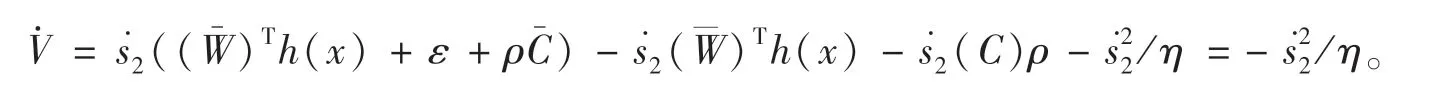
由于η＞0，ε→0，则≤0，满足Lyapunov 稳定性条件，故无人艇航向控制误差为渐进收敛，并趋于稳定。

3 仿真实验与分析

3.1 吊舱操纵模型回转运动仿真

无人舱的主要设计参数如表1 所示。

表1 吊舱无人艇的主要设计参数Tab.1 The main design parameters of thepod-type unmanned surface vehicle

根据表1 中无人艇参数计算吊舱推力及力矩，并对所构建模型进行回转操纵运动仿真研究。仿真结果如图5、图6 所示。

图5 吊舱转向角为30°的回转运动Fig.5 Rotation trajectory diagram of the pod with a steering angle of 30°

图6 吊舱转向角为45°的回转运动Fig.6 Rotation trajectory diagram of the pod with a steering angle of 45°

仿真结果表明，在30°和45°回转情况下，吊舱式无人艇的运动方向可保持稳定，保证了吊舱转向角的灵敏性和准确性。

3.2 吊舱式无人艇航向自适应滑模控制仿真

验证RBF 神经网络迭代滑模航向控制，对小型吊舱式无人艇航向控制进行仿真研究，并将仿真结果与等效迭代滑模和PID 控制的仿真结果进行对比。仿真参数设置：无人艇固定航速为1.67 m／s；螺旋桨转速为100 r／min；起始航向角为0°；期望航向角为45°。选取PID 控制器δ＝kPe＋kL∫edt＋，其控制参数为kP＝7.000，kL＝0.002，kD＝0.005；迭代滑模算法控制参数k1、k2、k3、k4分别为0.04，6.00，0.03，6.00；RBF 神经网络控制参数γ＝0.003，τ＝1000.0，ζ＝100.0，η＝0.2，并令隐含层数量i＝40，基宽参数bi＝1.5，中心位置cj均匀分布，分别取值为ci1∈（-20.0，20.0），ci2∈（-1.0，1.0），ci3∈（-0.5，0.5），ci4∈（-0.2，0.2）。

图7 无人艇航向变化曲线图Fig.7 Course change curve of unmanned surface vehicle

图8 吊舱转向角变化曲线图Fig.8 The change curve of the steering angle of the pod

在无干扰情况下，采用RBF 神经网络迭代滑模算法比等效迭代滑模控制、PID 控制收敛速度更快，航向控制趋于稳定状态。而且RBF 神经网络迭代滑模算法无超调，RBF 神经网络迭代滑模算法比PID 控制稳定时间快约20.1986 s，比等效迭代滑模稳定时间快约为7.5068 s。而且采用RBF 神经网络迭代滑模转向角的峰值最小，过渡过程趋于平缓，对吊舱推进器的使用寿命有益。

2）风、浪扰动下的仿真结果。设定风速为20 m／s；风向角为20°；有义波高为5 m；遭遇角为20°；吊舱转向角限制为35°；吊舱转向角速率限制为3°／s。在相同的干扰情况下，无人艇的仿真结果如图9、图10。

图9 风、浪干扰下无人艇航向变化曲线图Fig.9 Course change curve of unmanned surface vehicle under wind and wave interference

图10 风、浪干扰下吊舱转向角变化曲线图Fig.10 Change curve of pod steering angle under wind and wave interference

由图9、图10 可知，采用PID 控制的超调量为12.608%，等效迭代滑模算法超调量为10.396%，而RBF 神经网络自适应迭代滑模算法超调量为5.795%，且趋于稳定时间更短。在干扰情况下，RBF神经网络自适应迭代滑模能够保证航向变化历程与无干扰时基本一致，具有较强的鲁棒性。

4 结语

本文采用RBF 神经网络和迭代滑模算法补偿系统模型参数不确定及扰动影响，提高吊舱式无人艇航向控制稳定性。仿真数据表明，RBF 神经网络对吊舱式无人艇迭代滑模转向角控制律进一步优化，有效改进迭代滑模抖振现象，降低超调量，提高收敛速度，减小扰动影响，满足无人艇航行的稳定性。下一步将本文提到的吊舱式无人艇RBF 神经网络迭代滑模航向控制应用到实船中，进一步验证算法的有效性。