一种分离噪声盲源信号的FastICA 改进算法

方艺鹏，周海峰，张恩来，林开荣，郑东强，林忠华

（1.集美大学轮机工程学院，福建 厦门361021；2.福建省船舶与海洋工程重点实验室，福建 厦门361021；3.集美大学诚毅学院，福建 厦门361021；4.集美大学海洋装备与机械工程学院，福建 厦门361021）

0 引言

随着经济的发展，越来越多的大功率机械出现，使得噪声污染变得日益严重。针对这些大功率机械及动力设备的噪声控制，最有效的手段就是从噪声源入手［2］。其中准确识别噪声源以及确定噪声源的主次最为关键。经研究发现，大功率机械及动力设备的噪声源，由于其结构复杂，激励源众多且不可预测，属于典型的盲源信号。所以，识别噪声源的前提是将盲源信号进行分离。

独立分量分析（independent component analysis，ICA）算法是近几十年来在盲源分离方面运用最为广泛且有效的方法。这个算法最早是由Jutten 等［3］在1986 年提出来的，被广泛应用于语音信号处理、信号特征处理等领域。1997 年，Hyvarinen 等［4］在ICA 算法的基础上，研究并提出一种新的ICA方法，即快速独立分量分析（fast independent component analysis，FastICA）算法。相对于ICA 而言，该算法收敛速度更快。但是，该算法分离的信号在幅值、相位及排序等方面存在不确定性［5］。由于噪声的贡献度与能量大小有着密切的关系［6］，所以，对分离后的独立分量进行不确定性校正，对噪声源的识别以及确定噪声源的主次有着重大的意义。针对上述问题，本文提出一种改进的FastICA 算法，用于校正原算法因白化产生的不确定性。

1 FastICA 算法基本原理与改进

1.1 FastICA 算法原理

FastICA 算法，也称为基于固定点（fixed-point）的算法。该算法包含基于负熵最大、基于最大似然和基于峭度等三种不同的形式［10］。本文采用的是基于负熵最大的FastICA 算法作为基础。其负熵近似值的函数表达式为：J（yi）≈｛E［G（yi）］-E［G（vi）］｝2。其中：ki为常量；E［·］为计算数学期望；yi和vi为两个高斯随机变量；G为非二次函数。

FastICA 的算法过程为：

1）对观测信号X计算期望，并减去相应的期望值，也叫中心化处理；

2）对X做白化处理，做正交变换使得E［XTX］＝I；

3）选取待估计的数量m，并设定迭代次数i；

4）任取一个初始向量wi，该向量必须存在单位范数；

5）令w（i＋1）＝E［xg（wT（i）x）］-E［xg′（wT（i）x）］w（i），g（·）为G（·）的一阶导数；

6）wi标准化；

7）迭代后判断wi是否收敛，若不收敛则返回步骤5），若收敛则执行下一步；

8）令i＝i＋1，当i≤m时，跳回步骤4），否则结束算法程序。

1.2 FastICA 算法改进

由于FastICA 算法所分离出的独立分量yi存在幅值、相位和排序等方面的不确定性问题，特别是幅值和相位的问题，将会对噪声源的识别产生直接的影响。所以，本文提出一种基于最大相似准则与优化算法相结合的不确定性校正方法。该方法将与FastICA 进行衔接，达到在线校正的目的。该方法的流程图如图1 所示。

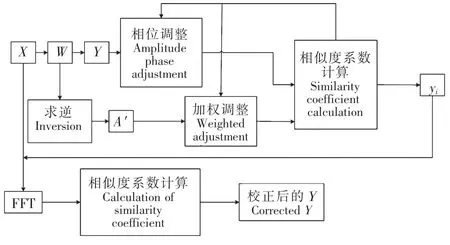
图1 不确定性校正流程图Fig.1 Uncertainty correction flow chart

1.2.1 相位调整

对FastICA 算法迭代后所得到的解混矩阵W（A-1）再进行求逆，即为初始的估计矩阵A′。

首先，对分离后的矩阵做相位调整。由于分离后的独立分量与源信号分量出现相位不确定性（一般为反相）［11］，故需要对分离出来的独立分量yj做180° 的相位调整。令，其中：εM为第M次相位调整函数，是初始的估计分量，经过εM次迭代后得到的估计分量。则有，其中aij为混合矩阵A中的元素。观测信号调整前后间的总相关系数的计算公式为：。其中：AC（·）为总相关系数；Xcor（·）为自相关系数。

然后，根据最大相似准则，寻找总相似度最大的值所对应的估计矩阵和独立分量arg max。由于M为正向或者反相，故M的取值为1，2，…，＋1。

当相位调整至正常时，此时的xi与的总相关系数将取得最大值，调整后出现反相的独立分量y均能恢复正常。

1.2.2 幅值调整

FastICA 算法的白化过程，使得分离后的独立分量在幅值上呈现的不确定性包含放大和缩小两种可能。故需要对aij乘以一个权值调整函数λN进行调整。由于无法预测权值分离分量的幅值变化情况，故采用以下算法进行权值的寻优。

首先，假设调整方向为正向，即权值加大。进行两次试探调整，得到相应的混合矩阵与，代入，可以得到调整后的观测信号，则总体相关系数相减式为：，判断U的正负即可知道相应的假设是否为真。通过该假设可以将λN的寻优区间缩减至原来的一半。

然后，将权值函数往该方向进行迭代寻优，采用一维搜索法。先用试点法进行模糊区间查询，得到大致的迭代区间。即当试点两个调整后的观测信号与xi之间的总相关系数出现先升后降的情况时，此时，二者的权值函数所对应的变量区间即为迭代区间。在该区间内采用黄金分割算法进行区间寻优，寻优终止条件为：＜1×10-3。

此时的λN为最理想的权值函数，并认为其对应的yi（N）幅值也恢复至与源信号基本一致。

1.2.3 排序校正

将经过幅值调整以及相位调整后的独立分量yi以及观测信号xi进行傅里叶变换得，可以得到相应的频谱。由于相位及幅值经过调整已经恢复（与源信号一致），寻优方式为：

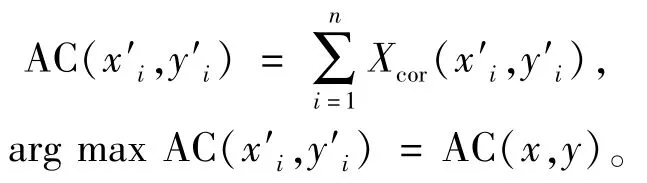
每个独立分量都进行相似度计算，最终得到相应的排列次序。

2 仿真实验验证

2.1 四种典型信号的仿真

在MATLAB 平台进行本算法的仿真实验。首先对四个较为典型的源信号Sn（t）（n＝1，2，3，4）应用改进后的FastICA 算法进行实验验证。四个典型信号分别是余弦信号S1、方波信号S2、正弦波信号S3和锯齿波信号S4。每个信号波形均设置200 个样本点。混合矩阵A采用的是4×4 的随机方阵。将源信号Sn（t）与矩阵A进行混合，可以得出观测信号Xn（t）。再通过FastICA 算法进行迭代计算，得到相应的分离信号Yn（t）。图2 为四个典型的源信号波形。

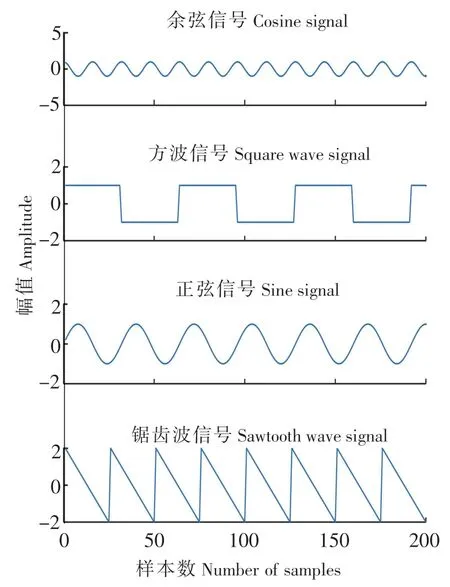
图2 源信号波形Fig.2 Source signal waveform

将源信号与矩阵A混合后，得到的观测信号如图3 所示，可以看出每一个源信号在经过与随机矩阵A的混合之后，波形明显发生变化。

图3 观测信号波形Fig.3 Observation signal waveform

用FastICA 算法处理信号，分离后得到的信号如图4 所示。由于用FastICA 算法处理信号时对信号做了白化处理，所以在分离之后出现幅值、相位以及排序发生了改变。

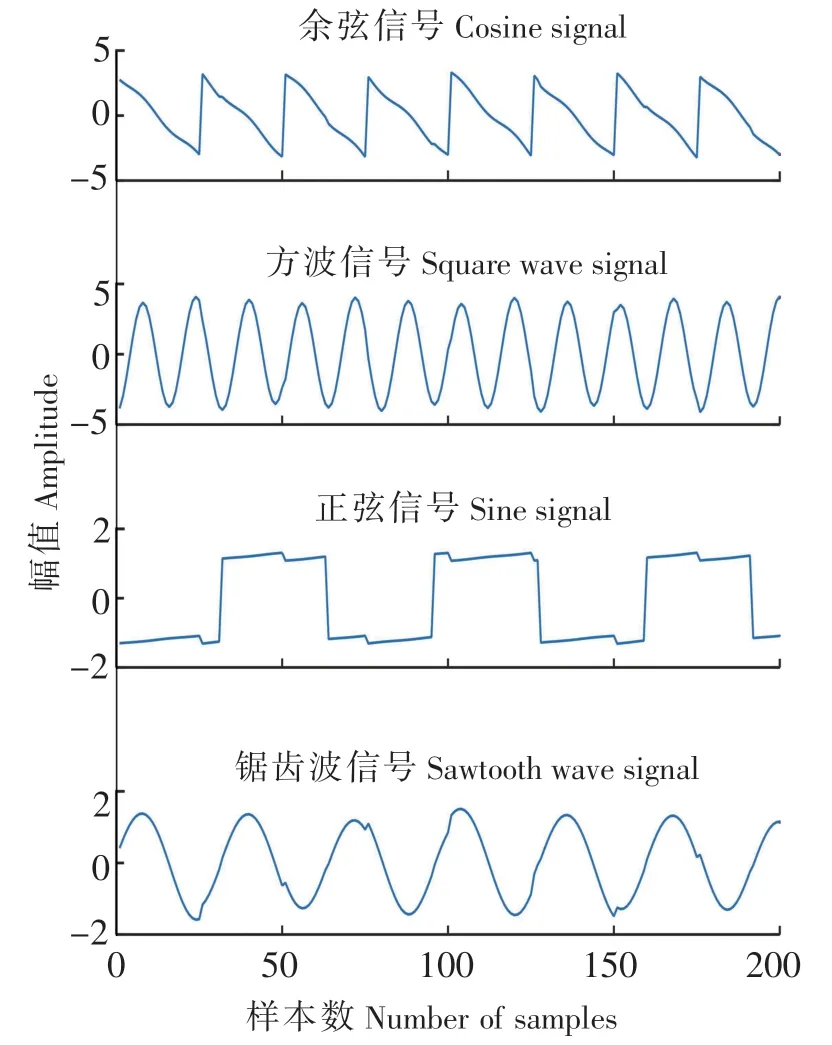
图4 分离信号波形Fig.4 Separate signal waveform

经过改进算法的计算，将源信号的不确定性加以消除，包括幅值、相位以及排序等。图5 是经过校正后得到的信号波形。校正后波形基本上恢复至与源信号相同。

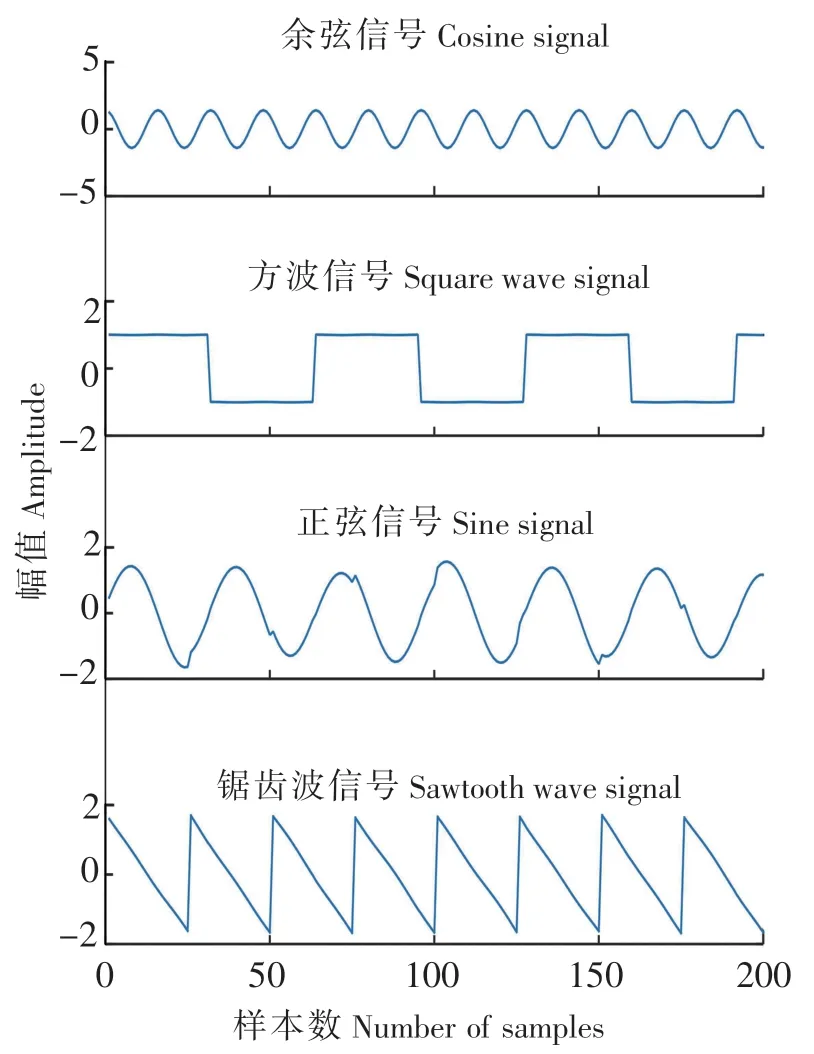
图5 不确定性校正后的波形Fig.5 Waveform after uncertainty corrected

对源信号、分离信号及校正后的信号进行FFT 分析，可得对应的频率幅值信息。由表1 可以看出，混合信号经新FastICA 算法校正后，得到的波形频率与源信号保持一致。相位及排序方面的信息由图2～5 对比能够很明显的看出，通过改进算法，已经得到了校正。

表1 4 种典型源信号与校正后信号的FFT 参数比较Tab.1 Comparison of FFT parameters of four typical signals between source signal and corrected signal

采用改进的FastICA 算法，分离校正前后的信号幅值与源信号幅值存在的偏差百分比如图6 所示。由图6 可以明显地看出，校正前后幅值的偏差差异巨大。校正后的波形幅值与源信号幅值基本保持一致，最大的偏差值不超过15%。由此可以看出，本改进算法能够有效地将FastICA 算法的不确定性进行消除。

图6 典型信号校正前后与源信号幅值的偏差百分比Fig.6 Percentage of amplitude deviation with typical source signal between before and after corrected

2.2 三段语音信号的仿真

为进一步验证，本研究还采用了三段语音信号进行混合、分离。其中语音信号的采样频率为44.1 kHz，采样点数为441 000。三段语音信号与三维随机矩阵A进行混合，得出相应的观测信号。图7 为语音信号的源信号波形，图8 为语音信号的观测信号波形。

图7 语音源信号波形Fig.7 Speech source signal waveform

图8 语音混合信号波形Fig.8 Speech mixed signal waveform

图9 为语音信号的分离信号波形。由波形可以看出经过FastICA 的白化处理，分离出的源信号在幅值、相位及排序方面均发生了变化。

图9 语音分离信号波形Fig.9 Waveform of speech separation signal

图10 为语音信号经过不确定性校正后的信号波形。由波形可以看出，该源信号波形的幅值、相位及排序问题基本得到了校正。

图10 不确定性校正后的语音信号波形Fig.10 Speech signal waveform after uncertainty corrected

对三段音频源信号和分离信号进行FFT 分析，可得分离前后信号的频率幅值信息。由表2 可以看出，混合信号用改进的FastICA 算法进行分离校正之后，得到的波形频率与源信号保持一致。

表2 三段音频信号与其校正后信号的FFT 参数比较Tab.2 Comparison of FFT parameters of 3 segment speech signals between source signal and corrected signal

由图11 可以明显看出，校正前的音频信号与源信号最大差距达到了2210%，幅值偏差巨大。而经过改进的FastICA 算法校正后的波形幅值，与源信号幅值基本保持一致，最大的偏差值不超过15%。通过音频信号的仿真，可更加明显地看出，本改进算法对分离信号的校正效果理想。

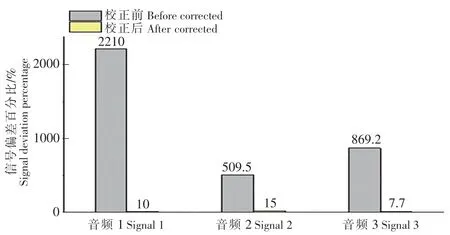
图11 音频信号校正前后与源信号幅值的偏差百分比Fig.11 Percentage of amplitude deviation with speech source signal between before and after corrected

3 结论

由于噪声的贡献度与能量之间有着直接的联系，所以噪声源信号分离的准确性对于后期的噪声识别有着至关重要的作用。本文所提出的改进FastICA 算法可以实现从混合的波形信号中分离出源信号波形，同时将波形的不确定性进行消除，达到较为完美的分离结果。盲源信号经过本算法的分离和校正之后，在幅值、相位等方面能最大程度地保真。这一结论为噪声源识别研究提供更加可靠的技术支持。