基于L*-格值逻辑上的直觉I-fuzzy 凸集
杨 帆,王瑞英
(内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022)
0 引言
1965 年,Zadeh[1]首次提出了凸模糊集的两种等价概念,描述了模糊集的凸性与普通集的凸性之间的密切联系。1980 年,Lowen 在文[2]中讨论了凸模糊集的分离定理,并研究了凸模糊集的拓扑性质。1986 年,Atanassov 在文[3]中给出了直觉模糊集的定义,增加了一个新的属性参数-非隶属度函数。20 世纪90 年代,应明生[4-6]运用连续值逻辑语义的方法在Fuzzy Set and Fuzzy Systems连续发表了三篇文章,奠定了不分明化拓扑学的基础。张广济等[7-8]给出了Fuzzifying 拓扑线性空间的定义,研究了Fuzzifying 凸集的代数性和拓扑性,讨论了直觉不分明化凸集的代数性。2019 年,王瑞英等[9]研究了I-fuzzy 凸集的代数性质。
本文在I-fuzzy 凸集相关理论的基础上,以L*-格值上的Lukasiewicz 蕴涵算子为工具,通过增加新的属性参数-非隶属度函数,给出了直觉I-fuzzy 凸集的定义,进一步讨论了L*-格值逻辑上的直觉I-fuzzy 凸集的代数性质。
1 预备知识
定义1[3]设E是一个论域,称A={<x,μA(x),νA(x)>:x∈E}为E上的直觉模糊集,其中,μA(x)∈[0,1]和νA(x)∈[0,1]分别为E中元素x隶属于A的程度和非隶属于A的程度,且满足条件:对于∀x∈E,0≤μA(x)+νA(x)≤1。
定义2[10]设X是线性空间,A和B是X上的两个直觉模糊集,则对于∀x∈X,(A+B)(x)=
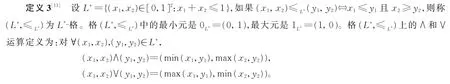
定义4[3]设A={ <x,μA(x),νA(x)>:x∈E}是E上的直觉模糊集,则
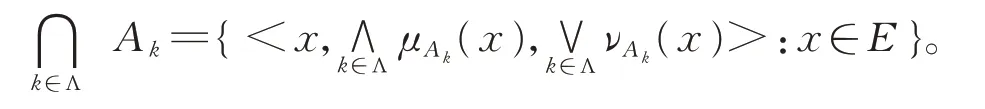
命题1[10]对于∀(x1,x2),(y1,y2)∈L*,
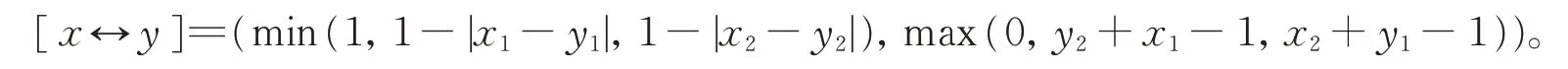
定义5[12]对于L-模糊点xλ,k∈K,k·xλ=(k·x)λ成立。
定义6[11]L*-格值上的Lukasiewicz 蕴涵算子定义为:对∀x,y∈L*,
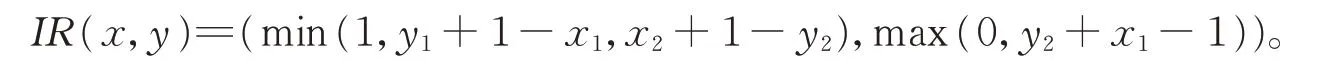
Lukasiewicz 蕴涵算子IR满足如下性质:
(1)单调律:(∀y∈L*)IR(·,y)在L*上是单调减的,且(∀x∈L*)IR(x,·)在L*上是单调增的;
(3)换质位法:(∀(x,y)∈(L*)2)IR(x,y)=
(4)可交换原理:(∀(x,y,z)∈(L*)3)IR(x,IR(y,z))=IR(y,IR(x,z));
引理1[8]本文用到的赋值公式:设α是论域X下的一个谓词,用记号[α]表示α的L*-格值,⊨α表示,记[α]=(x1,x2)∈L*,[β]=(y1,y2)∈L*。(1)[α∧β]=[α]∧[β];(2)[α→β]=IR([α],[β]);(3)[∀x(α(x))]=(4)[α↔β]=IR([α],[β])∧IR([β],[α])。
2 主要结果