基于数据挖掘技术的体育训练模式研究
赵 蕾
(西安翻译学院 体育部,陕西 西安 710105)
体育[1]是一门综合性很强的学科,包含了人文体育科学、体育社会科学等。随着计算机、信息技术飞速发展[2-4],特别是人工智能理论和数据挖掘技术的发展,为科学训练与先进的训练方法应用提供了良好的理论基础[5]。
统计分析是国内外常用的科学分析运动训练数据的方法[6]。王华满[7]结合数据挖掘技术,研究了一种改进的体育训练模式决策支持评估系统。容博尚[8]对大数据在体能训练中应用的可行性进行了研究。刘锦伟[9]基于数据挖掘技术开发了一套训练质量监控和临场战术统计系统,可为教练制定和调整训练计划起辅助决策作用。郝欢等[10]开发了一套体能训练管理系统,能够实现学员训练的数据的管理和分析,从而提高学员的体育训练水平。这些方法突破了以往教练员凭经验指导训练的现状,为科学训练提供了参考价值。
随着训练数据不断积累,常规的统计分析技术在训练数据的分析上可能存在不足,很难找到一个合适的模式来描述这些数据之间的相关性。数据挖掘的出现为在大量复杂的训练数据中发现科学规律和相关性提供了优化方法[11]。数据挖掘技术综合了统计学、人工智能、决策树、数据仓库和信息论等多学科技术,对运动训练指标进行综合分析。
为此,本文提出将数据挖掘技术应用于运动训练指标分析。根据数据集的特点,确定指标参数的分类,引入数据挖掘技术建立体育训练分析机制,构建分析模型。通过对数据准备、数据挖掘和结果解释三个过程的分析,得出训练指标的数据挖掘结果,完成数据分析。
1 相关概念
1.1 数据挖掘
一般情况下,数据挖掘过程可描述如下[12]:给定一组训练数据T,其中元素记录由多个属性描述,所有属性中只有一个属性作为类属性。令X=(X1,X2,…,Xn)为类属性集合,其中Xi(1≤i≤n)表示非类别属性并且可以具有不同的范围,当属性的值范围为连续时,称为连续属性;否则,称为离散属性。令C={C1,C2,…,Ck}表示具有k个不同类别属性集,则分类任务可描述为由数据集T确定从向量X到C的映射函数,即

进一步,可利用数据挖掘技术来表达隐函数H,有

其中:H为隐函数,H0表示函数的初始状态;p表示函数的定义属性;a表示元素记录的范围;n表示条件的范围;e表示运动指数的范围;f表示运动指数的离散指数。
1.2 训练过程分析
训练过程主要包括5 个环节,包括学生状态诊断、训练目标、训练计划、训练方案、目标完成评估,如图1所示。其中,训练分析是体育训练的关键环节。
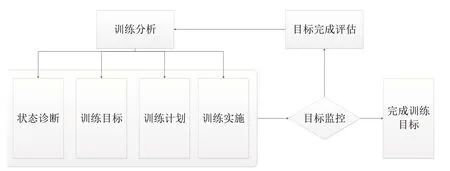
图1 训练实施过程Fig.1 Training implementation process
2 运动训练指标分析模型
2.1 基于粗糙集的数据预处理
粗糙集算法主要是在现有知识库的基础上,对知识的近似描述进行评估,消除数据处理资源中的冗余数据,获得更准确、更可靠的决策结果[13]。传统的粗糙集只能对分类资源数据进行评估和处理,而对数据的进一步处理需要离散化,这将导致信息和数据的缺失。本文采用邻域粗糙集方法对体育训练指标进行属性约简,并以环境因素为输入参数,对体育训练质量进行评价。本文规定决策集Dnt可定义为一个三元组,即

其中:U={x1,x2,…,xn}为数据集;D为体育训练的分类等级;A为属性集合。
基于此,将简约后的初始集设为空集,计算出该体育训练指标中剩余属性的显著性参数,如果这些显著性参数均不为0,则优先选择进入约简集中。该过程可总结如下:
步骤1∀α∈A,计算各个属性的临近关系矩阵Nα;
步骤2初始化属性粗糙集RED为空,且令φ→RED;
步骤3遍历属性A中所有RED未包含的属性,并计算各属性参数的重要性,即∀α∈A-RED,

步骤4选择具有最大重要性的属性αk,即

步骤5若αk>0,则将其添加入RED,且;否则跳转至步骤3,直到满足循环终止条件。
2.2 数据挖掘处理分析
数据挖掘处理分析分为三个步骤:数据选择、数据处理和数据转换。数据选择主要是从数据库中提取数据,形成目标数据。预处理是对提取的数据进行处理,使其符合要求。数据转换是减少数据的维数。初始特征函数的表达式为

其中:m为数据特征变量;I为数据可变性;N为目标数据;v为计算量;θ为拼写记录,l为挖掘范围;E为数据挖掘,E1为初始条件挖掘,E2为工作状态挖掘;i为第i级数据。
2.3 基于决策树的数据挖掘模型
决策树模型因其易于理解、可解释强等优点广泛应用于数据挖掘中[14]。决策树以树形结构表示最终的分类结果,表达式可描述为

式中:E0为理论表达式函数;n为计算长度;a为元素记录范围;f为离散指标;e为指标范围。
决策树可通过一系列规则对数据进行分类,可从一组不规则元素中推断出决策树表示的分类规则。一般情况下,决策树采用自顶向下的递归方法比较内部节点的属性值,并根据不同的属性值向下分支,其中叶节点是要划分的类。因此,从根节点到叶节点的路径即对应一个分类规则。图2 所示为一典型决策树构成,主要由决策节点、分支节点和叶节点三个部分组成。每个节点对应于一个非类别属性,每个分支对应于该属性的每个可能值,树的每个叶节点表示一个类别。树的中间节点通常用矩形表示,而叶节点用椭圆表示。然而,传统决策树容易受噪声和异常数据干扰造成冗余分支问题。
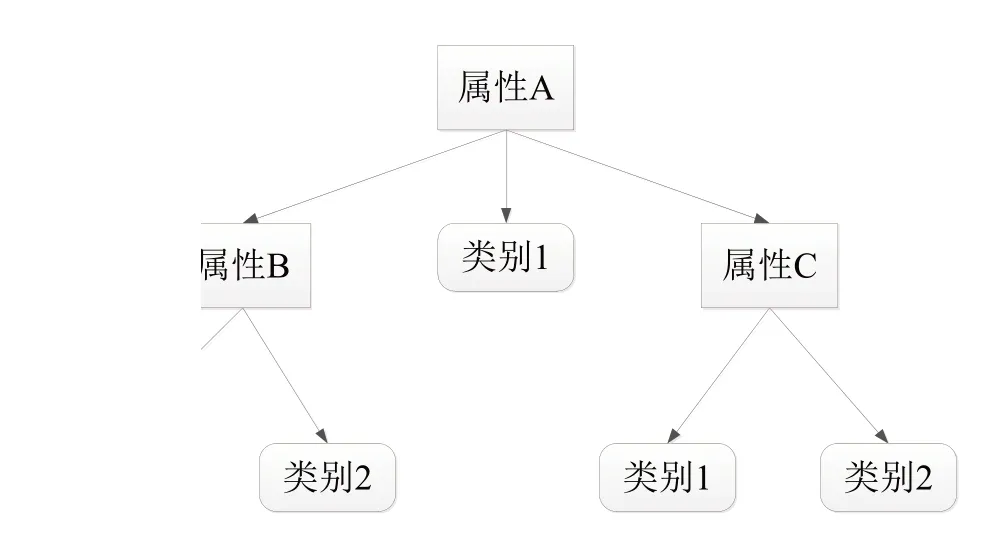
图2 典型的决策树构成Fig.2 Typical decision tree composition
为解决上述问题,图3 所示为本文改进的决策树算法。算法可分为学习和测试两个阶段。学习阶段采用自顶向下的递归方法训练参数;之后,将模型及参数带入测试阶段进行验证并对模型进行优化。该算法主要包括两个过程:其一是生成树;其二是对树进行剪枝,去除一些可能存在噪声或异常的数据。去除噪声和异常数据的公式为
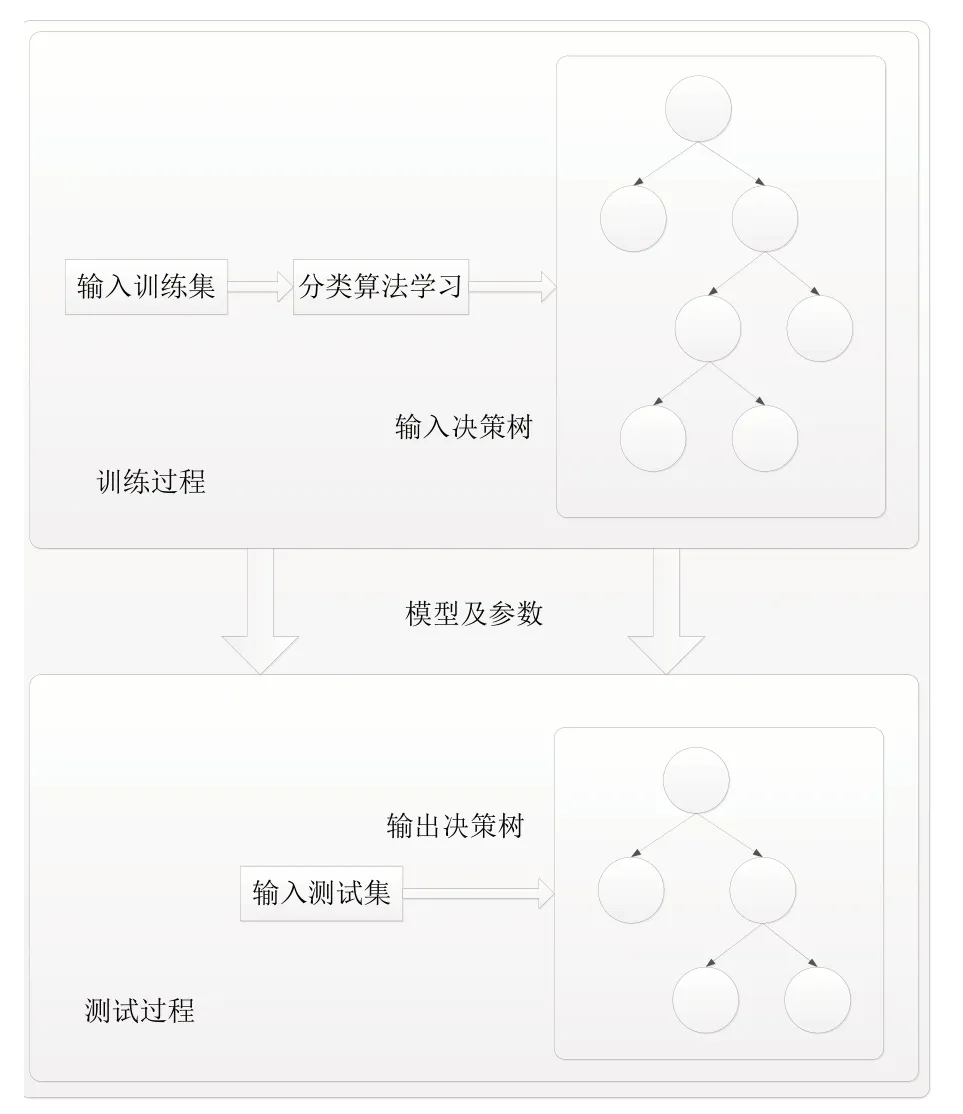
图3 改进的决策树生成过程Fig.3 Improved decision tree generation process
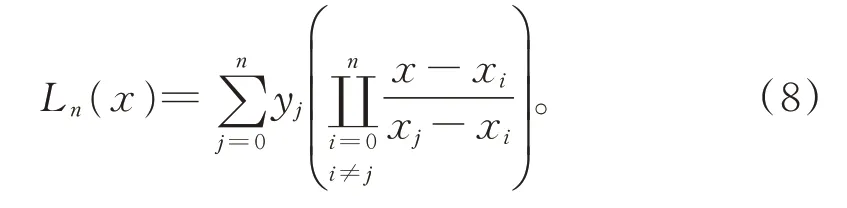
式中:Ln表示噪声去除函数;x表示数据集合,xi为决策树的第i层结果,同理xj为决策树的第j层结果;n表示搜索条件的范围。
3 仿真分析
3.1 仿真环境与数据准备
仿真环境为:windows10 操作系统下,i7 处理器,显卡GeForce GTX 1080,内存6 GB,并在python环境下编译程序。实验数据由本学院提供,包括2016-2020 年部分大学生体质测试项目(包括田径、球类、游泳、武术等)。剔除无用记录后,实验数据量为9860。
3.2 数据预处理
数据质量有很多评价因素,其中最重要的三个因素是准确性、完整性和一致性。但在实验所用数据集中,存在着不正确、不完整、不一致的数据,因此需要对数据进行预处理,从而提高数据质量,进而提高数据挖掘结果的质量。此外,不同运动的指标包含不同属性,如田径类以时间属性为标准,球类以得分、命中率、时间等属性为标准。为有效进行数据挖掘,可将每个属性的不同值映射到一系列整数,并使用整数替换该类别属性的值。如果存在(q×10)个属性类值,则每个原始值将唯一分配给区间[0,q] 中的整数。基于粗糙集的数据预处理后的数据及相关参数见表1。

表1 仿真数据及相关参数Tab.1 Simulation data and related parameters
3.3 数据挖掘结果
利用本文改进的决策树分析方法对体育训练指标进行分析,并与传统的聚类指标分析方法和神经网络方法进行对比,结果如图4 所示。从图4 的比较可以看出,改进决策树较其他两种方法训练成绩预测准确率更高。然而由于训练器材精度或记录误差等因素,本文所使用的样本数据具有一定程度噪声。因此,三种方法预测结果呈波动,且随着数据样本个数增多,整体预测准确率不断下降,这符合实际情况。此外,聚类方法在数据采样个数大于170 后,准确率急剧下降。分析其原因,一方面由于系统误差使得模型效果有所降低;另一方面数据中部分体育训练类型指标类似(如球类和射击,指标都包含得分、命中率),给聚类算法带来一定干扰。
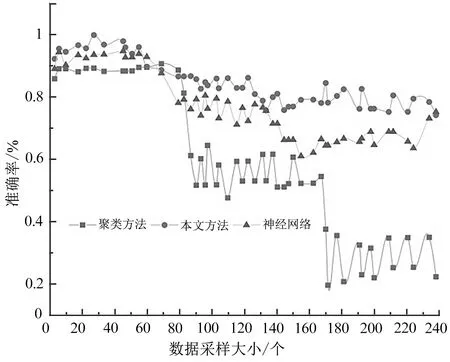
图4 不同方法模型预测准确率Fig.4 Prediction accuracy of different models
4 结论
体育训练过程积累了许多训练数据,常规的统计分析技术很难找到一个合适的模型来描述这些数据之间的相关性。数据挖掘的出现为在大量复杂的训练数据中发现科学规律和相关性提供了优化方法。为此,本文对数据挖掘、粗糙集、决策树模型进行分析,提出了数据挖掘技术应用于体育训练指标分析,为提高体育训练质量提供参考。

