基于多重分形去趋势波动分析算法的表面磨损形式特征研究*

张一兵 陈 聪 刘立鹏 胡 瑞

(1.武汉理工大学机电工程学院 湖北武汉 430070；2.中车株洲电机有限公司 湖南株洲 412000；3.南昌工程学院机械与电气工程学院 江西南昌 330000)

摩擦表面形貌直接反映了机械零件的磨损、疲劳和腐蚀等特征行为，不同的摩擦表面状态会影响摩擦副的性能。在一定的工作环境下，互相接触、相对运动的零件表面在摩擦磨损过程中，会因为不同的磨损形式对摩擦磨损表面造成不同的影响，并影响摩擦部件的性能和耐久性，所以分析确定摩擦磨损表面的磨损形式对提高零部件摩擦学性能的研究有着重要意义[1]。通常粗糙表面形貌具有非平稳性和随机性[2]，应用分形理论可解决在粗糙表面接触、摩擦、磨损、磨屑等方面的复杂问题，有利于分析摩擦系统的非线性行为[3]。对于具有统计自仿射分形特征的粗糙表面，传统表面评定参数由于测量尺度的原因，其表征能力具有一定的局限性。分形理论在表面表征上虽然解决了尺度限制的问题，但分形理论的单一分形并不能完全描述其表面特征[4]。多重分形在表征方面避免了其单一性，使得多重分形能够更加全面地评价粗糙表面特征[5-6]。在多重分形研究方面，刘烨等人[7]采用多重分形谱中的谱宽度定量表征了气缸套磨损表面的形貌特征和表面的高度均一性;WANG等[8]通过多重分形去趋势波动分析方法(MF-DFA)提取了植物叶片的纹理特征并用于植物物种分类。此外还有一些研究[9-11]是针对具有非线性的信号进行多重分形处理，如摩擦信号、振动信号以及声发射信号来分析刀具或零件的磨损状态等。而在与摩擦学相关的表面纹理研究方面，多为研究零件表面微织构对零件性能的影响，以及利用图像处理方法对磨损后的表面纹理进行分析。由于图像处理转化成三维形貌数据的过程中，在一定程度上会影响数据的准确性，因此利用直接测量的大量表面形貌数据，再应用先进的数据处理和分析方法对磨损表面进行研究，可保证数据的准确性。但目前对于磨损后表面纹理和磨损形式之间关联的特征研究文献较少。

由于磨损形式对磨损表面的纹理特征具有较大的影响，通过对磨损表面的纹理特征的表征研究，有利于对磨损表面的磨损形式进行识别。本文作者使用研制的LSTM-1型磨损表面形貌测量仪采集了不同载荷下的黏着、磨料2种摩擦表面形貌数据，采用稳健高斯滤波[12]方法提取其包含磨损特征的高频信息后，再应用MF-DFA方法计算广义赫斯特(Hurst)指数，分析广义Hurst指数与磨损形式之间的关系，给出了磨损表面纹理特征的表征参数——广义Hurst指数，最后使用主成分分析法对广义Hurst指数提取了识别2种磨损形式的特征参数，用于机器学习分类,并分析不同分类器的准确率。

1 多重分形理论与MF-DFA算法

1.1 多重分形理论

多重分形所刻画的是分形测度在支集上的分布情况[6]，即使用一个多重分形谱函数f(α)～α，其中α是奇异性指数，通过改变阶数q的值，分析表面形貌数据在不同尺度下的分形特征,进而定量表征磨损表面的粗糙度信息。多重分形去趋势波动分析方法(MF-DFA)在处理表面包含非平稳测度的非自然纹理[13]的数据时，能够消除表面形貌数据中的不良趋势。文中针对不同磨损形式的表面使用MF-DFA分析其磨损纹理特征，提取用于机器学习中识别磨损形式的特征。

1.2 MF-DFA算法

多重分形去趋势波动分析算法是对去趋势波动分析(DFA)方法的改进，可用于分析具有多重分形特性非平稳序列的长程相关性和标度不变性。文中采用文献[14]给出的二维MF-DFA算法，利用MatLab软件编程实现磨损表面形貌数据的二维MF-DFA算法。具体步骤如下：

(1)将表面形貌数据看作M×N矩阵X(i,j)，其中i=1,2,…,M,j=1,2,…,N。为了保证所有的表面形貌高度数据为正值，将X(i,j)中的最小高度值作为参考平面，再将表面划分成Ms×Ns(Ms=[M/s],Ns=[N/s],[]符号表示向下取整)个等长s的非重叠正方形子域。将划分的每个正方形子域记为Xm,n,其中Xm,n(i,j)=X(v+i,w+j)，1≤i,j≤s,v=(m-1)s,w=(n-1)s。

(2)对所有的子域Xm,n(i,j)累积求和。求和公式如式(1)所示

(1)

其中1≤i,j≤s。

(3)利用最小二乘法拟合每个表面Gm,n的局部趋势。文中选取式(2)所示双变量多项式函数进行拟合：

(2)

其中1≤i,j≤s，a、b、c、d、e、f是待定参数，可从最小二乘法平面拟合得到。

(4)建立残差矩阵。利用式(1)与式(2)之差，可以得到式(3)所示的残差矩阵：

(3)

(5)各子域Xm,n(i,j)的去趋势波动函数定义如下：

(4)

第q阶波动函数的计算如式(5)、式(6)所示：

(5)

(6)

(6)通过改变尺寸标度s的值,确定去趋势波动函数Fq(s)和s之间的幂律关系，可以得到：

Fq(s)∝sh(q)

(7)

其中s在[6,min(M,N)/4]区间范围内取值。由式(7)可以得到广义Hurst指数h(q)，当q=2时的广义Hurst指数h(q=2)，即为赫斯特(Hurst)指数。对于每一个q值，由MF-DFA计算得到的h(q)和多重分形理论得到的质量指数τ(q)之间存在式(8)所示关系：

τ(q)=qh(q)-Df=qh(q)-2

(8)

其中Df是支撑集的分形维数。

经试算，考虑到计算效率和数据的冗余性，文中q=-10～10，取值步长为1，共21个取值。

2 磨损试样制备及数据采集

2.1 磨损试样制备

参照文献[12]的试验方式，在XP-2型数控摩擦磨损试验机上进行销-盘试验，其中磨盘试样的材料为35钢，尺寸为φ58 mm×8 mm，销试样的材料为Cr12MoV，尺寸为小径φ4 mm，大径φ10 mm，长度26 mm，销的摩擦表面为小径端。销和盘试样的表面粗糙度Ra分别为0.78～0.85 μm和0.41～0.46 μm。在不同载荷条件下共进行了6组磨料磨损和黏着磨损2种磨损形式的试验，具体试验参数如表1所示。

表1 试验工况参数设置

为了得到磨料磨损和黏着磨损2种典型磨损形式的表面形貌，采用了2种不同的润滑方法进行试验。(1)磨料磨损：采用质量比为1∶10的金刚砂研磨膏和润滑油的混合液作为润滑介质，通过试验在盘试样表面获得磨料磨损形貌特征。(2)黏着磨损:采用微量润滑油润滑方式，使摩擦表面处于边界润滑状态，在试验过程中随着润滑膜的破裂，摩擦表面容易黏着从而得到黏着磨损的形貌特征。

表2给出了不同载荷下由试验得到的磨料磨损和黏着磨损盘试样表面局部显微图。

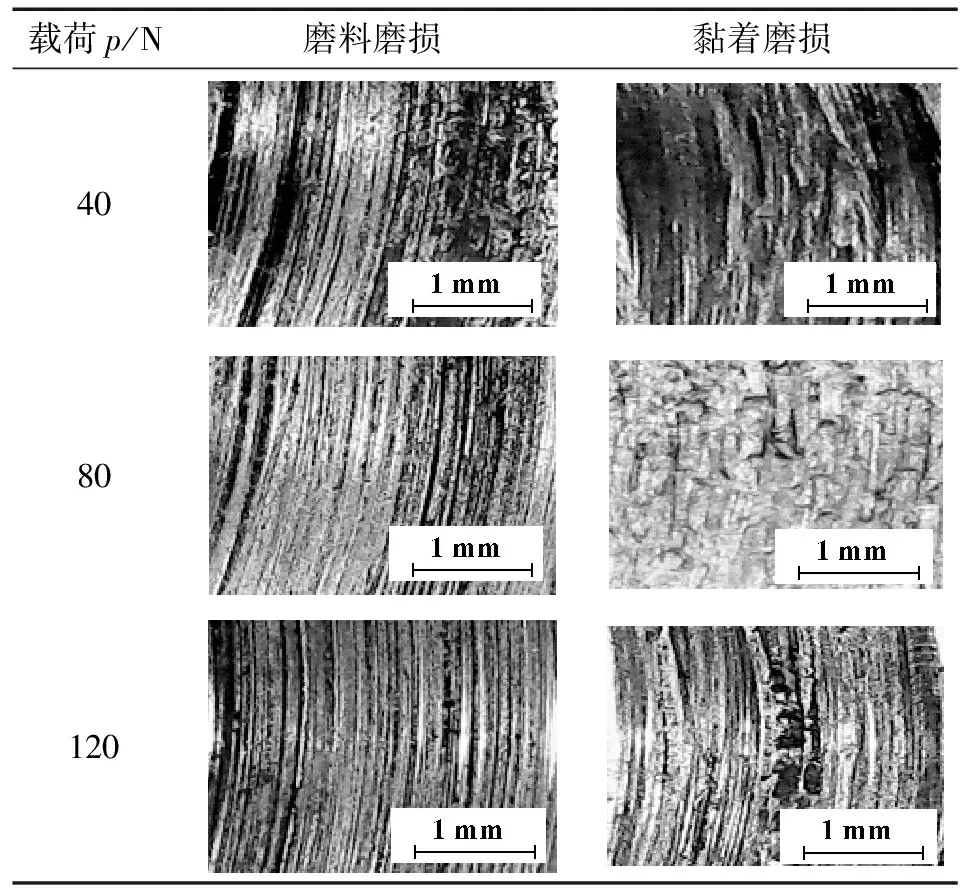
表2 不同载荷下磨料磨损和黏着磨损表面显微图

2.2 磨损表面形貌数据采集

采用研制的LSTM-1型磨损表面形貌测量仪[12]对盘试样磨损表面形貌进行测量和数据采集。为了保证磨损表面形貌样本数据的随机性,选择在每个试样盘表面磨痕中随机采集10组表面形貌数据。每组采集面积为1.2 mm2的正方形区域，由此得到磨料磨损和黏着磨损的表面形貌数据样本各30组，并将采集到的数据样本用于后续的磨损特征分析及机器学习识别分类应用中。

3 磨损形式特征分析

由于采集到的磨损表面形貌数据中包含表面粗糙度、波纹度和形状误差，因此为了消除表面波纹度和几何形状误差的影响，应用稳健高斯滤波将表面形貌中包含磨损特征的高频信息提取出来用于磨损表面的MF-DFA研究。

应用MF-DFA方法对载荷为40 N盘试样的磨损表面形貌数据进行分析计算得到的结果如图1和图2所示。图1所示是磨损表面形貌不同阶数q值下的去趋势波动函数Fq(s)与尺寸标度s的双对数坐标图，图2所示是质量指数τ(q)与阶数q的关系。根据对于不同q值，Fq(s)与s都具有对数线性关系，以及τ(q)是关于q的凸函数时，得出MF-DFA所处理得到的数据具有多重分形特性的结论[14]，由图1和图2可知，试验得到的磨损表面形貌中的高频信息具有多重分形特性。

3.1 磨损形式特征的广义Hurst指数分析

根据去趋势波动函数Fq(s)和尺寸标度s以及广义Hurst指数h(q)之间具有式(7)所示的关系：Fq(s)∝sh(q)，因此可求出不同磨损形式表面所对应的广义Hurst指数，探讨广义Hurst指数与磨损表面纹理特征之间的关系。表3给出了在磨料磨损和黏着磨损盘试样上，选取相同半径圆周位置测量的10组表面形貌。表3中区域编号1为一个试验以磨料磨损为主的盘试样，试验结束后，在盘试样上采集到的磨料磨损和局部黏着磨损形式的表面形貌和广义Hurst指数-阶数q的变化曲线；区域编号2～5为试验以磨料磨损和黏着磨损为主的2个不同盘试样上分别采集的表面形貌和广义Hurst指数-阶数q的变化曲线，其中区域编号5最右边的表面形貌为试验以黏着磨损为主的盘试样上采集到的局部磨料磨损形式的表面形貌。

从表3中各区域编号所对应磨损形式的表面形貌可以看出，对于磨料磨损表面，表面犁沟形纹理特征明显，犁沟两边具有明显的垅形峰，表明磨料磨损表面具有方向性较强的纹理特征；对于黏着磨损表面，表面分布着不规则的凹坑和凸台，黏着磨损表面具有方向性较弱的纹理特征。针对磨料磨损和黏着磨损这2种磨损表面纹理特征，对照区域编号1以磨料磨损为主的同一个试样盘上的2种不同磨损形式的广义Hurst指数曲线分布可以看出，黏着磨损的广义Hurst指数随阶数q的变化曲线分布于磨料磨损的曲线之上；同样在区域编号2～4中，对于不同盘试样上的2种磨损形式的广义Hurst曲线也有与区域编号1相似的规律，说明广义Hurst指数对黏着磨损和磨料磨损的方向性纹理特征具有敏感性，而在区域编号5中，对于不同试样盘上相同磨损形式的表面形貌，其广义Hurst曲线近乎重合，说明广义Hurst指数在判断相似磨损表面纹理特征的时候仍然具有一定的有效性。

为了验证上述规律的一般性，对40、80、120 N载荷下各组广义Hurst指数均值的变化情况进行了分析，分别得到10组磨料磨损和10组黏着磨损的广义Hurst指数均值曲线分布，如图3所示。可知，不同磨损形式的广义Hurst指数曲线之间仍表现出与表3分析结果相同的区分性。因此由以上分析可以得出：广义Hurst指数能够表征黏着和磨料磨损表面的纹理特征，即广义Hurst指数对磨损表面的犁沟、垅形峰、凹坑、凸台等磨损特征具有较好的分辨能力，因此可将广义Hurst指数作为识别这2种磨损形式的特征。

表3 2种磨损形式的表面形貌及其广义Hurst指数曲线

3.2 基于主成分分析的磨损形式特征提取

在机器学习中，特征提取的主要目的是从数据收集和特征生成技术获取的特征中，通过去除这些特征中的冗余和不相关信息来尽可能多地保留相关信息。文中对磨损形式特征的MF-DFA分析中，由于阶数q的取值为-10～10，故广义Hurst指数为21维特征，因此需对其进行特征提取。主成分分析法(PCA)是一种通过降维把多个变量转变成少数几个主成分的统计分析方法，即用尽可能包含大部分信息的几个主成分来代替全部变量的信息。通过线性变换，使得每个主成分都是原始变量的线性组合，同时各个主成分之间互不相关，然后计算各主成分的方差贡献率(占原变量信息总量的比重)和累积方差贡献率，提取累积方差贡献率不低于85%的前几个主成分[15]作为新的特征。文中选取累积方差贡献率为95%的前2个主成分T1、T2作为新的特征，由表1实验数据利用PCA方法计算得到主成分T1、T2各60个，作为机器学习磨损形式识别模型的输入数据。

4 磨损形式识别分类

采用PCA计算得到的2个主成分T1、T2作为输入特征，将黏着磨损和磨料磨损2种磨损形式的分类结果分别编码为0和1作为输出，然后使用K-means聚类、支持向量机(SVM)和BP神经网络3种机器学习模型对2种典型磨损形式进行训练和分类，其中训练集和测试集分别为总样本点的70%和30%。为了保证SVM分类的精度，使用了5折交叉验证来防止模型的过拟合和欠拟合，同时利用网格搜索方法来确定模型的最佳参数。表4给出了各分类器的最佳参数及识别结果，其中K-means只需确定参数K(类簇为2)。SVM中的C为惩罚因子，核函数为sigmoid函数，BP神经网络栏中的l1、l2为隐含层的神经元数。

表4 各分类器的最佳参数及识别结果对比

从表4中测试集正确率可知，BP神经网络分类结果最佳，SVM的正确率比K-means稍好。图4和图5所示分别为K-means聚类和SVM的磨损形式分类图。从图4中可以看出，2种磨损形式的类簇样本点聚集较为集中，2种类簇分布较为清楚，但存在少量离群点，这是因为计算结果中有异常偏大点，即该点对应的磨损程度较其他点更为严重，如图4右侧黏着磨损中的偏离样本点。从图5所示SVM的分类图来看，SVM的决策边界对2种磨损形式分类结果的划分后，磨料磨损和黏着磨损的分类样本点中存在相互的嵌入点，即未被正确分类的样本点，这是因为磨料磨损和黏着磨损形式的磨损表面形貌中存在交叉的磨损特征，即以磨料磨损为主的表面可能包含了部分黏着磨损的表面纹理特征，以黏着磨损为主的表面也可能包含部分磨料磨损的表面纹理特征，因此对于两类磨损形式的样本，机器学习模型存在分类结果正确率降低的现象。

5 结论

以黏着磨损和磨料磨损为研究对象，使用MF-DFA分析2种磨损形式的表面纹理特征，提取了识别2种磨损形式的特征，并通过机器学习模型对2种磨损进行了识别分类，得出下述结论：

(1)载荷为40、80、120 N工况下，具有多重分形特性的黏着磨损表面的平均广义Hurst指数大于磨料磨损表面的平均广义Hurst指数，说明广义Hurst指数可用于区分磨损表面犁沟类和凹坑类纹理特征的指标，作为磨损形式识别的机器学习特征。

(2)基于MF-DFA提取的广义Hurst指数作为识别黏着和磨料磨损2种磨损形式的特征，在BP神经网络和SVM分类中识别正确率分别达到79%和84.21%，说明广义Hurst指数在磨损形式识别的研究中具有实用价值。在后续研究中，可通过增大数据样本量或在以广义Hurst指数为主特征基础上，增加其他辅助特征来完善机器学习模型的泛化能力，提高模型的识别正确率。