Ψ压缩在不同图度量空间中的N阶不动点定理
梁晓楠,王诗云,赵金阳
(沈阳航空航天大学 理学院,沈阳 110136)
不动点理论在非线性微分方程、非线性积分方程等方面有广泛的应用。巴拿赫压缩原理于1922年被首次提出[1]。随后,一些数学家改进推广了这一原理,并讨论不同空间上各种映射下的不动点定理。1977年,Matkowski[2]提出了一个关于Ψ函数的压缩,得出了很多关于Ψ压缩的结论。2004年,Ranand等[3]利用Ψ压缩建立了偏序度量空间上的不动点理论。
自从2006年Bhaskar等[4]给出二阶不动点的定义后,一些二阶、三阶和N阶不动点定理相继出现。Lakshmikantham等[5],Sharifa等[6],Sintunavarat等[7]利用Ψ压缩研究了偏序度量空间中的二阶不动点定理。Amini-Harandi[8]得到了三阶不动点定理。2008年,Jachymski[9]在具有图度量空间上建立了一些不动点理论。这些结果推广和统一了具有偏序阶度量空间中的一些结果。此后,许多学者开始研究带图度量空间上的不动点理论,丰富了不动点的理论知识[10-12]。
本文主要从两个方面进行研究:一是利用Ψ压缩构建不动点定理;二是研究不同图的N阶不动点理论。第1部分讨论具有一个图的度量空间上的Ψ压缩不动点定理。第2部分讨论具有不同图的度量空间上的N阶不动点定理。在这一部分中,考虑在同一集合上不同的图(xn,G)=(X,G1)×(X,Gi)×,…,×(X,Gn)构造了一个N阶不动点定理。
1 一阶不动点定理
用(X,d,G)表示具有图G的度量空间(X,d),借用文献[9]中引入的“保边”和“G-连续”的定义。

定义2对f:X→X,∀x,y∈X,如果(x,y)∈E(G),就有(f(x),f(y))∈E(G),则称f:X→X是保边的。
在下面的研究中,需要用到以下两个假设。
假设(A1):X中的任一序列(xn)n∈N,对于任意的n∈N,如果xn→x并且(xn,xn+1)∈E(G),则(xn,x)∈E(G)。

定理1设f:X→X是完备度量空间X上的一个映射。定义xf={x∈X:(x,f(x))∈E(G)}。如果:
(i)f是保边的;
(ii)xf≠φ;
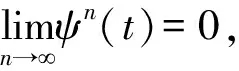
(iv)f是G-连续的,或者假设(A1)成立。
则f有一个不动点。
证明:当t∈(0,∞),由[13,th1.2]可知,ψ(t) 不失一般性,设x0∈xf且x0≠f(x0)。因为(x0,f(x0))∈E(G)以及f是保边的,有 (fn(x0),fn+1(x0))∈E(G)其中n≥1 同时 d(fn(x0),fn+1(x0))≤ψ(d(fn-1(x0),fn(x0))) ≤ψ2(d(fn-2(x0),fn-1(x0))) ≤… ≤ψn(d(x0,f(x0))) 如果f是G-连续的,易得x=f(x)。假定假设(A1)成立,有(fn(x0),x)∈E(G)并且(fn+1(x0),f(x))∈E(G)。因此,对于n≥1时 d(x,f(x))≤d(x,fn+1(x0))+d(f(x),fn+1(x0)) ≤d(x,fn+1(x0))+ψ(d(x,fn(x0))) ≤d(x,fn+1(x0))+d(x,fn(x0)) 这意味着f(x)=x。 定理2如果定理1的假设加入假设(A2)则f的不动点是唯一的。 那么, 对n≥1,有 这是矛盾的。 本节讨论在(X,d)上赋予不同图时的N阶不动点理论。例如,(X,d,G)来表示具有图G的度量空间(X,d),那么G-1可以认为是另一个独立的图G′=G-1,记作(X,d,G′)。这一转变拓宽了研究的范围和视野。把F:Xn→X的N阶不动点问题转化为F:Xn→Xn的不动点问题。 设(X,d)是非空的度量空间,在同一个集合X里定义N个不同的图,记为(X,d,Gi)。设F:Xn→X是一个给定的映射。 对于x:=x(1)=(ξ1,ξ2,…,ξn),定义x(2):=(ξ2,…,ξn,ξ1),…,x(N):(ξn,ξ1,…,ξN-1)。 定义3称F:XN→X是保边的。若任意x,y∈XN,(ξi,ηi)∈E(Gi),有(F(x(i)),F(y(i)))∈E(Gi),i=1,2,…,N。 定义5称x=(ξ1,ξ2,…,ξn)为F:XN→X的N阶不动点,若 ξ1=F(x),ξ2=F(x(2)),…,ξN=F(x(N)) 定义(X,D,G)如下:X=XN,V(G)=X,并且任意x,y∈X,E(G)和D分别定义为式(1)和式(2): (x,y)∈E(G)⟺(ξi,ηi)∈E(Gi) (1) D(x,y)=d(ξ1,η1)+d(ξ2,η2)+,…,+d(ξN,ηN) (2) 定义:X→X为式(3) F(x)=(F(x),F(x(2)),…,F(x(N))) (3) 显然F的不动点是F的N阶不动点。 类似假设(A1)与假设(A2),提出下面两个假设: 假设(A3)对于i=1,2,…,N,并且X里任意序列(xn)n∈N有xn→x,如果(xn,xn+1)∈E(Gi),对于任意n∈N,则(xn,x)∈E(Gi)。 假设(A4)对于任意x,y∈xn,存在某一点z∈xn有 定理3设(X,d,Gi)其中i=1,2,…,N是图Gi下的完备度量空间,设F:XN→X是一个映射满足: (i)F是保边的; (ii)φ≠{x=(ξ1,ξ2,…,ξn)∈X:(ξi,F(x(i)))∈E(Gi),i=1,2,…,N}; d(F(x),F(y))≤ψ1(d(ξ1,η1))+ψ2(d(ξ2,η2))+,…,+ψn(d(ξn,ηn)) (iv)F是NG-连续的或者假设(A3)成立。 证明:根据公式(1)~(3)可知,F是保边的,XF≠φ 并且F在X上是G-连续的或者假设(A1)成立。显然,F的不动点是F中N阶不动点,只需证明定理1的条件三成立。以三阶的情况为例加以证明,N阶的情况同理。 D(F(x),F(y))= d(F(x),F(y))+d(F(x(2)),F(y(2)))+d(F(x(3)),F(y(3)))≤ψ1(d(ξ1,η1))+ψ2(d(ξ2,η2))+ψ3(d(ξ3,η3))+ψ1(d(ξ2,η2))+ψ2(d(ξ3,η3))+ψ3(d(ξ1,η1))+ψ1(d(ξ3,η3))+ψ2(d(ξ1,η1))+ψ3(d(ξ2,η2)) =ψ(d(ξ1,η1))+ψ(d(ξ2,η2))+ψ(d(ξ3,η3)) ≤ψ(d(ξ1,η1)+d(ξ2,η2)+d(ξ3,η3)) =ψ(D(x,y)). 由定理1可知F有一个不动点,这个不动点是F中的三阶不动点。 注:定理3的条件(iii)不能改为: 例 1设X=R具有欧几里得度量|.|,对于任意a,b∈X,认为如果a≤b那么(a,b)∈E(G)。(R3,D,G)被(R,|.|,G)推断出:对于x,y∈R3,(3.4)定义了(x,y)∈E(G),并且D(x,y)=|ξ1-η1|+|ξ2-η2|+|ξ3-η3|。定义F:R3→R有 其中tant是正切函数,并且 d(F(x),F(y))=|F(x)-F(y)| 另一方面,如果F有三阶不动点x=(ξ1+ξ2+ξ3),然后 把上面的3个公式加起来,得到 这意味着 这是矛盾的,所以F的三阶不动点不存在。 推论2假定(X,d,G)是图G完备的度量空间,设F:XN→X是一个映射满足以下条件: (i)F是保边的; (ii)φ≠{x=(ξ1,ξ2,…,ξn)∈X:(ξi,F(x(i)))∈E(Gi),i=1,2,…,N}; (iii)有N个常数l1,…,ln有l1+l2+,…,+ln<1 d(F(x),F(y))≤l1d(ξ1,η1)+l2d(ξ2,η2)+,…,+lnd(ξn,ηn) 对于y∈X有(ξi,ηi)∈E(G); (iv)F是NG-连续的, 推论3对于i=1,2,…,N,如果i是奇数,有Gi=G;如果i是偶数,有Gi=G-1。(X,d)是一个完备的度量空间。假定F:XN→X是一个映射满足: (i)F是保边的; (ii)φ≠{x=(ξ1,ξ2,…,ξn)∈X:(ξi,F(x(i)))∈E(Gi),i=1,2,…,N}; (iii)有N个常数l1,…,ln且l1+l2+,…,+ln<1 d(F(x),F(y))≤l1d(ξ1,η1)+l2d(ξ2,η2)+,…,+lnd(ξn,ηn) 如果i是偶数,(ξi,ηi)∈E(G),如果i是奇数,(ξi,ηi)∈E(G-1); (iv)F是NG-连续的, 本文为利用ψ压缩理论来讨论N阶不动点理论提供了一个新视角,拓宽了研究的范围和视野,使得证明过程简洁明了。其结果推广了最近的一些关于N阶的不动点结果。



2 N阶不动点定理
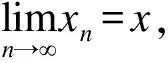







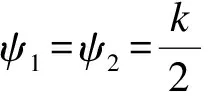
3 结论

