航空发动机进口导叶调节机构误差分析

国 强，刘公博，严冬梅,杨治中

(中国航发沈阳发动机研究所第二研究室，沈阳 110015)

随着发动机性能的不断提高，风扇工作点逐渐靠近边界，此时风扇的工作状态较敏感，若进口流量匹配不好，风扇发生喘振的可能性极大，造成严重后果[1-3]。因此，进口导叶调节角度的偏差直接影响发动机性能。

目前，航空发动机在整机和部件试验过程中，进口导叶调节机构经常暴露出调节精度不足的问题，导致进口导叶在不同工作状态下实际转角与理论转角存在偏差。当发动机相对换算转速较低时，主要影响发动机的喘振裕度，严重时在过渡态可能发生喘振。当发动机相对换算转速较高时，若角度偏差导致流量增大，则会降低发动机喘振裕度，极有可能导致风扇发生喘振；若角度偏差导致流量减小，则降低发动机的推力，导致推力不达标。因此进口导叶调节精度成为衡量发动机可靠性的重要因素，也是影响发动机性能进一步提高的关键因素。

贺飞等[4]通过齐次坐标分析的方法，结合MATLAB软件推导出典型结构形式涡轴发动机调节机构运动学方程，并得到调节规律；文献[5-6]等以单极可调静子叶片调节机构为研究对象，在CATIA中建模，导入ADAMS中仿真，得到静子叶片在±30°范围内无突变调节；杨伟等[7]通过UG建立压气机三级联调机构模型，导入ADAMS中仿真，得到不同换算转速下三级联调机构的转角误差值。文献[8-10]提出了一种以三维参数化仿真为核心，进行压气机静叶联调机构方案设计的方法；文献[11-13]基于机构学的相关理论对几种可调静子叶片调节机构系统中的摇臂与联动环的连接结构进行运动学和动力学仿真分析；文献[14-16]从数学建模、数值仿真及试验研究3方面对可调静子叶片调节机构的运动特性进行了研究。

本文在某型号发动机进口导叶调节机构基础上进行分析，建立了机构运动学模型，推导出作动筒伸出量与导叶转角之间的函数关系；在UG中建立调节机构模型，导入ADAMS中进行仿真，验证数学模型的准确性；在数学模型的基础上，推导出调节机构误差分析模型，得到各主要参数对导叶转角精度的影响情况，提取出对转角精度影响较大的敏感参数，并提出了提高转角精度的方法。

1 进口导叶调节机构作动原理

发动机进口导叶调节机构结构如图1所示，作动筒伸长后，带动L型杆转动，L型杆通过拉杆带动联动环实现绕发动机轴线的转动和沿发动机轴线的移动，多个沿圆周均布的摇臂与联动环相连，摇臂另一侧与进口导叶相连，各个进口导叶随着联动环的运动实现绕自身轴线转动，即通过控制作动筒伸出量来实现进口导叶转角的控制。

图1 进口导叶调节机构结构构成

2 数学模型建立

按照结构方案的传力路线：作动筒—L型杆—拉杆—联动环—摇臂—进口导叶，其中拉杆长度为固定量，利用拉杆长度建立等量关系，通过建立多个空间局部坐标系，将作动筒伸长量与进口导叶转角数学模型分如下3步建立。

(1)进口导叶绕自身轴线转角θ与联动环绕发动机轴线转角γ和沿发动机轴线位移Δy的函数关系；

(2)作动筒伸出某一长度后L型杆绕自身转轴转动角度；

(3)建立基础坐标系，分别得到拉杆两侧的球副中心在基础坐标系中的坐标表示，利用拉杆长度为常量，推导出作动筒伸长量与进口导叶转角的函数关系见式(1)

(1)

其中

xH′、yH′、zH′分别为拉杆与联动环相连球副中心在基础坐标系中的坐标；

xK′、yK′、zK′分别为拉杆与L型杆相连球副中心在基础坐标系中的坐标。

3 仿真分析

为使整个调节过程中进口导叶转角无突变且随着作动筒的伸出能够均匀变化，作动筒的伸长量与导叶转角之间的线性关系越强越好。

针对建立好的数学模型，通过MATLAB对其进行仿真，得到进口导叶转角与作动筒伸长量的关系见图2所示。通过仿真结果可知，二者近似成线性关系，且整个变化过程无突变。

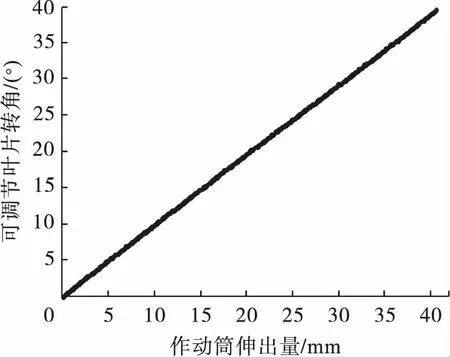
图2 MATLAB仿真导叶转角与作动筒伸长量关系

为验证数学模型推导的准确性，在UG中完成调节机构各零件的建模和装配，如图3所示，将模型导入到ADAMS中，根据发动机实际使用过程中机构中各零件选取的材料牌号对机构各零件定义材料属性，除作动筒和关节轴承为钢材外，机构中其余件均为钛合金。完成材料属性定义后在作动筒处建立驱动，在各关节连接处建立运动副，如图4所示，并在ADAMS完成机构运动学仿真，得到进口导叶转角与作动筒伸长量关系见图5。

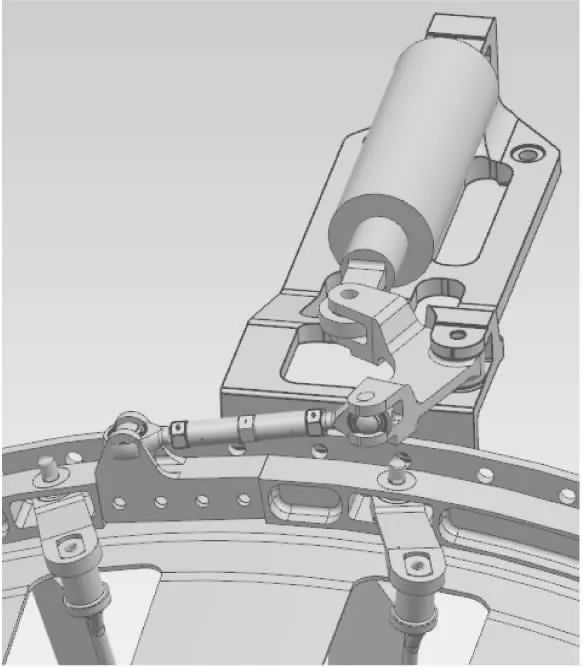
图3 UG中完成调节机构虚拟装配

图4 ADAMS中仿真模型

图5 ADAMS仿真导叶转角与作动筒伸长量关系

ADAMS仿真结果与MATLAB仿真结果一致，验证了数学模型推导的准确性。

4 误差模型建立

作动筒伸长量与进口导叶转角的数学模型如式(2)的函数所示

F(Lla,Lyb,θ,Llz,Llc,Llg,U,V,W,β)=0

(2)

其中

Lla为拉杆与联动环相连球副中心到发动机轴线距离，Lyb为摇臂两端运动副中心距离，θ为进口导叶转角，Llz为L型杆主动臂长度，Llc为L型杆从动臂长度，Llg为拉杆长度；U为L型杆转动中心在基础坐标系中的x值，V为L型杆转动中心在基础坐标系中的y值，W为L型杆转动中心在基础坐标系中的z值，β为进口导叶旋转轴线倾斜角。

对式(2)函数进行全微分得到式(3)

(3)

其中dLla、dLyb、dθ、dLlz、dLlc、dLlg、dU、dV、dW、dβ为各参数的误差值，进而得到进口导叶的误差模型如式(4)所示

(4)

5 误差分析

为分析调节机构各主要参数对调节精度的影响，得到对机构精度影响较敏感的参数，以下分别考虑单一参数对误差的影响，考虑某一参数存在误差时其余各参数均假定误差为零。为量化分析，人为给定各主要参数一个相同的误差值，在机构各参数输入误差一定的情况下，分析不同参数对调节精度影响的大小，以识别出对机构误差影响较大的敏感参数。人为给定误差如下：

dLla=1 mm、dLyb=1 mm、dLlz=1 mm、dLlc=1 mm、dLlg=1 mm、dU=1 mm、dV=1 mm、dW=1 mm、dβ=1°，得到作动筒伸出量与各参数对导叶转角偏差的影响规律如图6所示。

图6 各参数对导叶转角误差影响规律

通过上述误差分析，得到对导叶转角误差较大的参数为：Lyb、Llz、Llc、Llg、U，其对导叶转角偏差的影响均大于0.38°，因此将上述参数定义为对机构精度影响较大的敏感参数。其余参数Lla、V、W、β，对导叶转角偏差的影响均小于0.13°，因此将这些参数定义为对机构精度影响较小的非敏感参数。

由上述分析得到，给定各参数相同的误差值时对导叶转角误差的影响大小是不相同的，进而得到了对机构精度影响较大的敏感参数。进一步对仿真出的误差曲线进行分析可知，给定各参数的均为1 mm正向误差，但得到的导叶转角误差却有正负之分，误差为正说明对导叶转角的影响是偏开方向的，误差为负说明对导叶转角的影响是偏关方向的，由此可知，当给定各参数误差为-1 mm时，得到导叶转角误差的正负就会与之前相反。因此，通过上述分析可知，通过不同参数给定误差正负的组合，使各参数对导叶转角误差影响的正负互相抵消，可以在不改变各参数误差大小(即不提高零件加工精度)的情况下，有效降低导叶的转角误差。

某型号发动机调节机构各参数公差数值如表1所示，在保持各参数实际公差带宽度不变的基础上，人为调整各参数公差的正负，如表2所示，使各参数对导叶转角误差影响的正负尽可能互相抵消，仿真出导叶转角偏差如图7所示，可知导叶转角误差最大为0.298°左右。再次调整各参数公差的正负，如表3所示，使各参数对导叶转角误差影响的正负尽可能相同，仿真得出导叶转角偏差如图7所示，可知导叶转角误差最大达到约0.943°。由此可知，各参数给定公差正负的不同组合，对导叶转角误差有着重要的影响，在不改变各参数公差带宽的情况下，通过公差正负的合理组合，能够有效降低导叶的转角误差，提高调节精度。

图7 各参数公差正负的组合对导叶转角误差的影响规律

表1 某型号发动机各参数公差数值

表2 对导叶转角误差影响正负互相抵消时各参数公差数值

表3 对导叶转角误差影响正负相同时各参数公差数值

6 结论

本文在某型号发动机进口导叶调节机构基础上进行了相关分析,并得到如下结论:

(1)建立了机构数学模型，推导出作动筒伸出量与进口导叶转角之间的函数关系，由仿真曲线可知二者近似成线性关系，且整个调节过程曲线无突变，说明导叶转角随着作动筒伸长能够平滑均匀变化，有利于保证机构作动效率，并能够提高调节精度；

(2)在数学模型基础上建立机构误差分析模型，每次分析仅考虑单一因素的影响，得到对导叶转角误差影响较大的敏感参数，进而通过与生产加工单位协调，综合考虑生产成本和加工周期，对敏感参数可以适当收严公差；反之不敏感的参数可以适当放松公差，设计出既有利于提高机构调节精度，又能降低生产成本，缩短生产周期的不同参数公差值，该结论能够直接指导方案详细设计；

(3)各主要参数误差的正负直接影响导叶转角误差的方向，因此，在不改变各参数公差带宽的情况下，通过公差正负的合理组合，使各参数对导叶转角误差影响的正负尽可能互相抵消，能够有效降低导叶的转角误差，提高调节精度，进而提高发动机性能和运行稳定性。