基于差分进化的卷积神经网络的文本分类研究

钟桂凤,庞雄文,孙道宗

(1.广州理工学院计算机科学与工程学院,广东 广州 510540) (2.华南师范大学计算机学院,广东 广州 530631) (3.华南农业大学 电子工程学院,广东 广州 510642)

互联网飞速发展,大规模网络文本数据分析研究应运而生,通过分类,将网络中的数据进行归档整理,提高数据管理的有效性. 网络文本的格式不标准及编码方式的多样性[1],以及文本长度的差异性,使得文本分类的难度提升. 在采用深度学习的文本分类中,由于普通文本不同于变量属性特征,可以直接进行输入并通过深度学习训练而获得结果,在文本分类之前,需要通过向量转换,然后进行训练获得分类结果,这种方法对分类精度造成了影响,因此需要进一步优化深度学习算法,以提高深度学习对文本分类的适用度.

当前关于文本分类的研究较多,于游等[2]对常见的中文文本分类方法做了系统阐述,比较了各类方法对于不同文本的适用度及优缺点,给后续文本分类算法研究提供了借鉴;郭超磊等[3]采用SVM方法进行中文文本分类,可以达到一定的分类效果,但分类准确度不高,且对分类样本的格式要求严格,对网络各种符号及文字混合的文本分类适用度不高;Shu等[4]对学习推荐开展了研究,提出了基于潜在因素模型的CNN文本分类模型,分类精度高,但是基于内容的CNN结构存在分类效率及稳定性不理想的问题. 本文采用卷积神经网络对普通文本进行分类,为了提高文本分类的性能,引入差分进化(differential evolution,DE)算法对网络参数进行优化求解,并对差分算法的缩放因子采取自适应策略,以提高优化求解精度,通过差分进化优化的卷积神经网络算法,可以有效提高文本分类精度及RMSE性能.

1 理论基础与模型设计

1.1 自适应DE算法

设种群规模为N,属性维度为D,差分缩放因子为F,交叉速率CR,每个个体的取值为[Umin,Umax],则第i个个体 的j维属性可表示为[5]:

xij=Umin+rand×(Umax-Umin),

(1)

式中,i=1,2,…,N,j=1,2,…,D,rand为(0,1)随机数.

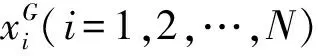
(2)

式中,i≠r1≠r2≠r3,r1、r2和r3为第G代中除了编号为i的个体之外的随机3个个体.F常见取值[0,2].

个体交叉方法为[7]:

(3)

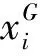
(4)

式中,f表示适应度函数.当达到最大代数Gmax时,DE算法停止.

F常见取值[0,2],DE的优化过程与F值密切,F值不合适将会造成差分进化算法的优化性能不高的问题,因此在计算时引入自适应F值[8].Fmin和Fmax范围为[0,2],则:

(5)

F值随着进化代数G的变化而逐渐变小,前期进化追求种群多样化,后期注重搜索能力,这样DE算法更容易获得最优个体.

1.2 卷积神经网络模型设计

设文本样本集X=(x1,x2,…,xN),m个文本属性特征通过第l层卷积运算得[9]:

(6)

式中,klj和blj分别表示l层对特征j赋予的权重及偏置,*为卷积,f(·)为:

(7)

对N个样本的m个特征进行卷积,卷积核尺寸(kernel size)h×w,按照公式(8)进行:

(8)

令M=N/(h×w),那么原样本X=(x1,x2,…xN)经过卷积池化后重新得到的样本为X′=(x1,x2,…,xM).

然后X′进行转换运算[10]:

(9)

限制条件为:∑aij=1,0≤aij≤1.

根据公式(9)得到CNN所有连接层,最后选择分类器预测样本类别.

设第k个节点的训练输出和实际值分别为yk和dk,则误差项δk为:

δk=(dk-yk)yk(1-yk).

(10)

假设第l、l+1层分别包含L和P个节点,则第l层节点j的误差为[11]:

(11)

式中,hj为输出,Wjk为神经元j到l+1层神经元k的权重,更新方法为:

(12)

式中,η为学习率.

偏置Δbk(n)的更新方式为[12]:

(13)

式中,α为偏置更新步长,一般α=1.调整后的权重为:

wjk(n+1)=wjk(n)+Δwjk(n).

(14)

调整后的偏置为:

bk(n+1)=bk(n)+Δbk(n).

(15)

所有节点的误差E为:

(16)

当E满足设定的阈值,迭代停止,获得稳定的CNN模型.

图1 分类流程Fig.1 Classification process

1.3 DE-CNN模型的分类流程

在运用CNN对文本进行分类之前,首先需要对待分类的样本数据进行word2vec转换[13],这主要是为了解决文本属性的向量化过程,转换后的Skip-gram便于进行CNN的有效输入. 建立了CNN文本分类模型之后,将随机权重和偏置通过DE算法优化求解,根据文本分类准确度函数建立适应度函数,通过DE的多代进化,获得权重和偏置最优个体,最后CNN进行分类训练获得文本分类结果.

2 实例仿真结果与分析

为了验证差分进化的卷积神经网络算法在文本分类中的性能,进行实例仿真. 首先,对不同的差分进化算法参数进行性能仿真,其次对不同卷积核尺寸的性能进行仿真,最后将本文算法与常用文本分类算法进行性能对比仿真.

文本分类仿真的数据来源为SST(stanford sentiment treebank)和THUCnews新闻数据. 其中SST数据样本11 852个,5个类别;而THUCnews选取了7类共计10 500个新闻样本. 通过算法对新闻文档进行分类,从而能够实现新闻自动归档. 样本具体分布结构如表1所示.

表1 THUCnews文本集Table 1 THUCnews text set

对从表1中的文本采用word2vec得到Skip-gram结构,从而完成了本文至属性向量映射,这样文本样本就可以进行CNN分类训练. 在仿真过程中,THUCnews和SST样本集分别按照总样本容量的7∶2∶1的比例数量进行训练、测试和验证.

本文DE算法设置的初值Fmin=0.2,Fmax=0.9,CR=0.1,Gmax=100. CNN卷积核默认2*2.

2.1 不同卷积尺寸文本分类性能

采用不同kernel size的CNN结构分别对THUCnews和SST样本进行仿真.

从表2可得,选择卷积核尺寸为3*3效果最佳,THUCnews的数据样本分类准确率到了92.16%,而SST数据样本分类准确率达到了93.27%. 当尺寸增大时,2个数据集的分类准确率和标准差均在下降,这是因为卷积尺寸过大,造成了卷积粒度大减少了样本重要属性参与卷积及转换运算的机会.

表2 分类准确率Table 2 Classification accuracy

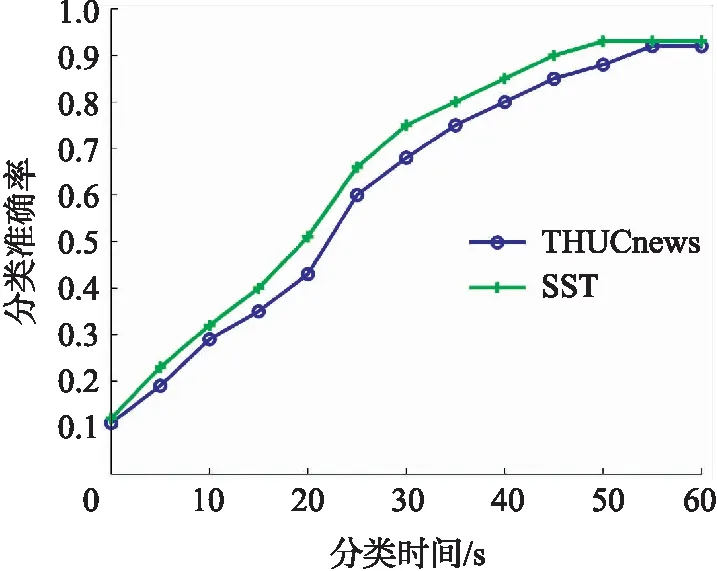
图2 分类准确率(卷积核3*3)Fig.2 Classification accuracy(convolution kernel 3*3)

对比发现,DE-CNN算法对SST的分类性能优于THUCnews数据集,这可能是因为THUCnews类别数较多而不易分类造成的. 当卷积核尺寸为3*3时,DE-CNN算法在THUCnews和SST数据集的收敛时间性能如图2所示.

从图2得,在卷积核设置为3*3时,DE-CNN算法在THUCnews数据集的分类时间约为55s,而在SST数据集的分类时间约为50s,这主要是因为THUCnews集的类别比SST集多的原因. 2个样本收敛时的分类准确率均超过了0.9.

2.2 DE算法的优化性能

为了验证DE算法对CNN的优化性能,分别采用CNN算法和DE-CNN算法对THUCnews集和SST集的样本进行性能仿真.

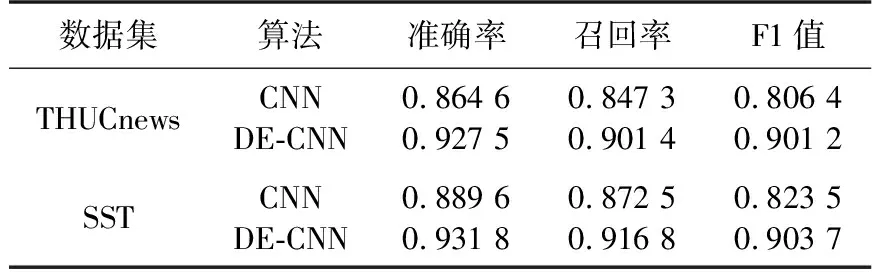
表3 CNN和DE-CNN算法的分类性能Table 3 Classification performance of CNN and DE-CNN algorithms

从表3可以看出,在3种不同数据集的文本分类中,经过了DE优化的CNN算法表现出了更优的性能. 对于3个样本集,DE-CNN文本分类的3个指标均超过了0.9. DE-CNN的最大分类准确率为93.18%,CNN最大分类准确率仅为88.96%,准确率提升明显. 这主要是因为经过DE的权重优化后,CNN获得了更优的权重和偏置初值,从而获得了更准确的文本分类性能,下面将继续对两种算法的收敛性能进行对比.

从图3和4得,DE-CNN相比于CNN的收敛性能优势明显. 在THUCnews数据样本分类中,DE-CNN收敛时RMSE约为0.18,而CNN收敛的RMSE值约为2.5;而在SST数据样本分类中,DE-CNN收敛时RMSE约为0.16,而CNN收敛的RMSE值约为2.2,因此DE-CNN算法相比于CNN算法的分类稳定性更好. 在收敛时间方面,对于2种不同的样本集,CNN比DE-CNN收敛的时间少5s左右,这可能是因为DE算法求解最优权重和偏置的时间消耗,但从整个DE-CNN分类时间来看,DE算法消耗的时间占比很小,对文本分类时间影响较小.

图3 2种算法的RMSE值(THUCnews集)Fig.3 RMSE values of the two algorithms(THUCnews set)

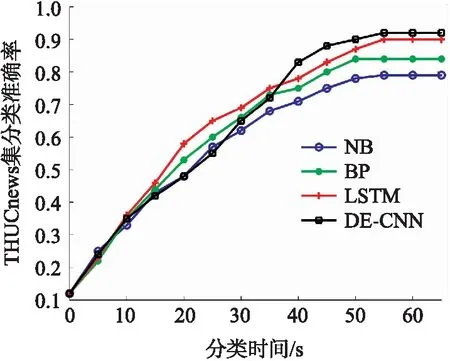
图4 2种算法的RMSE值(SST集)Fig.4 RMSE values of two algorithms(SST set)

2.3 不同算法的文本分类性能

采用常用朴素贝叶斯(NB)[14]、神经网络(BP)[15]、LSTM神经网络(LSTM)[16]和本文算法分别对THUCnews和SST数据集进行仿真.

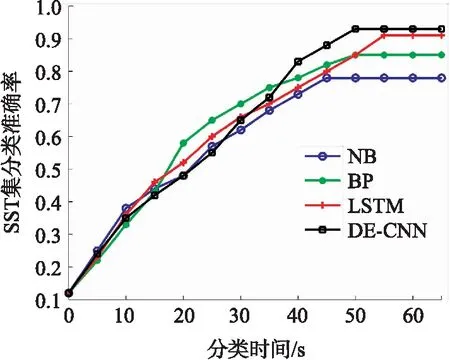
图6 4种算法的分类准确率(SST数据集)Fig.6 Classification accuracy of four algorithms (SST dataset)

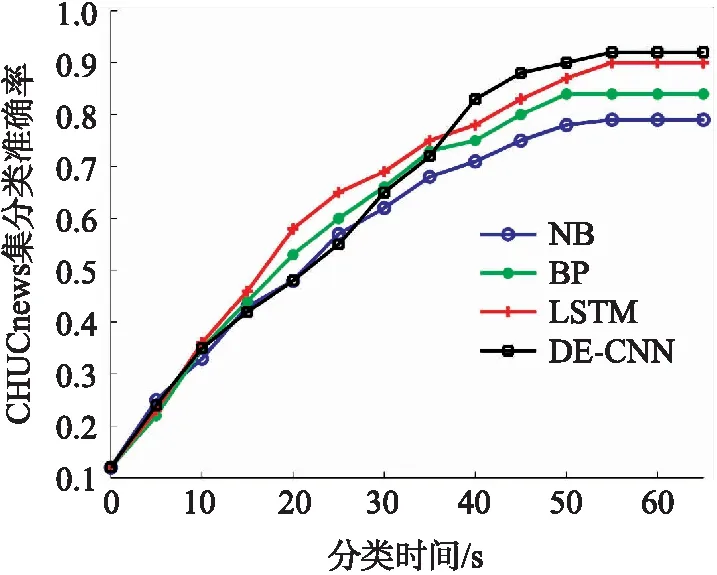
图5 4种算法的分类准确率(THUCnews数据集)Fig.5 Classification accuracy of four algorithms (THUCnews dataset)

从文本的分类准确率来看,DE-CNN和LSTM算法的分类准确率最高,稳定时两者的分类准确率非常接近,且均超过了0.9,NB的分类准确率最差,均小于0.8. 从分类时间方面来看,对于THUCnews和SST数据集,LSTM算法消耗时间最长,DE-CNN算法次之,NB算法最省时.

下面继续对4种算法在文本的分类稳定性进行仿真,验证4种算法的准确率RMSE性能.

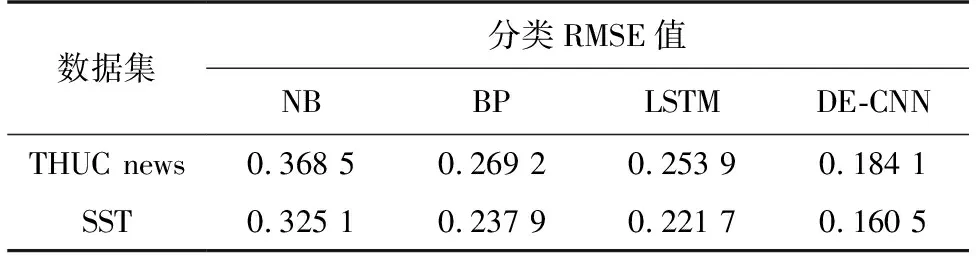
表4 不同算法的准确率RMSE性能Table 4 Accuracy and RMSE performance of different algorithms

从表4的RMSE性能中可以看出,对于2种数据集,DE-CNN算法的分类准确率RMSE值最优,NB表现最差. 相比而言,4种算法在SST集的RMSE性能表现更优,这可能是因为SST集待分类的类别数较少,而THUCnews需要分类的类别数较多,在文本分类时,类别过多造成了分类准确率值在多次分类中波动较大,这也说明分类准确率RMSE值对分类类别数影响敏感. 综合而言,对于THUCnews新闻集和SST情感集的文本分类,对比常见分类算法,在获得较高分类准确率的条件下,本文算法仍能获得较好的分类时间和RMSE性能.

3 结论

采用差分进化的卷积神经网络算法应用于文本分类,充分利用差分进化算法的权重优化求解优势,提高了卷积神经网络算法在文本分类中的适用度,相比于常用文本分类算法,本文算法在分类准确率及RMSE性能方面优势明显. 后续研究将进一步调整差分进化参数,以提高文本分类时间性能.