改进粒子速度和位置更新公式的粒子群优化算法

李二超,高振磊

(兰州理工大学电气工程与信息工程学院,甘肃 兰州 730050)

粒子群优化(Particle Swarm Optimization,PSO)算法是美国心理学家Kennedy和电气工程师Eberhart受鸟类和鱼类觅食行为启发而提出的一种基于群体智能理论的演化计算技术[1]. 该算法因其计算内存需求少、控制参数少等优点得到广泛关注,并被应用于求解诸多实际优化问题,如路径规划[2]、优化调度[3]、参数辨识[4]、图像分割[5]等.

然而,标准PSO算法存在一些固有缺陷,如搜索精度低、局部搜索能力差,尤其求解复杂非线性多峰函数时容易陷入局部极小解出现“早熟”收敛[6]. 针对以上缺陷,国内外学者做了大量改进研究,其中对粒子速度和位置更新公式的改进是研究热点之一. Shi等[7]首次在速度更新项中引入随迭代次数线性递减的惯性权重w,以更好平衡算法全局开发能力与局部勘探能力. Liu等[8]指出PSO算法求解过程本身就是一个非线性过程,w呈非线性变化能更好改善算法性能,因此他提出基于Logistic混沌映射的非线性变化的w.对w的改进还有基于余弦函数[9]和基于Sigmoid函数非线性变化的w[10]等. Deep等[11]将粒子速度更新公式中个体最优和群体最优替换为二者线性组合,以此来增大粒子的搜索空间,从而使算法有更多可能搜索到全局最优解. 胡旺等[12]提出一种简化PSO算法,尝试舍弃粒子速度项,由个体最优粒子和群体最优粒子来引导粒子更新,实验结果表明这种改进极大提高了算法性能. Liu等[13]在简化PSO算法[12]基础上,引入粒子“维数信息”概念,将粒子位置更新分解为3种模式,3种模式分别具有改善全局开发能力、改善局部勘探能力、提高算法收敛速度的功能,并基于概率来选择相应模式更新粒子位置. 陆松建等[14]在文献[11-12]的基础上提出一种均值简化粒子群算法,该算法舍弃速度更新项,将文献[11]对速度更新项的改进思想用于对位置更新的改进. Zhang等[15]提出2种不同的位置更新公式,并在算法不同迭代时期选择相应公式,以此来改善算法性能. Liu等[8]在文献[15]的研究基础上,在当前粒子适应度值与种群中所有粒子的平均适应度值之间建立一种数学关系pi,提出一种自适应位置更新策略来更好平衡算法的全局开发能力和局部勘探能力. Cheng等[16]基于社会学习的思想,改进速度和位置更新机制,粒子速度和位置更新时不再向个体最优和群体最优学习,而向一些优于自身的个体学习.

本文结合以上分析,借鉴文献[8,11-13]的改进思想,提出一种新的粒子位置和速度自适应更新策略,引用文献[8]中的自适应判定机制,并将文献[13]提出的粒子维度信息引入粒子速度更新公式,将其与其他6种改进PSO算法在12个不同类型的测试函数上进行寻优测试,证明了本文所提算法的有效性.

1 相关工作

1.1 标准粒子群优化算法

标准PSO算法中,粒子通过学习自身历史经验(pbest)与群体经验(gbest)寻找最优粒子. 对于求解变量为X={x1,x2,…,xD}、目标函数为min{f(x)}的优化问题,标准PSO算法粒子更新公式为式(1)和式(2).

vid(t+1)=wvid(t)+c1r1(pbestid-xid(t))+c2r2(gbestd-xid(t)),

(1)

xid(t+1)=xid(t)+vid(t+1),

(2)

式中,vid(t+1)和xid(t+1)分别为粒子i在t+1代的速度和位置;w是惯性权重,标准PSO算法中w随迭代次数线性递减;c1和c2为学习因子,通常取值为2;r1和r2是[0,1]均匀分布的随机数.

1.2 粒子速度更新公式的改进

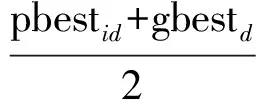
(3)

图1 MeanPSO算法和PSO算法粒子进化过程Fig.1 Particle evolution process of MeanPSO algorithm and PSO algorithm

MeanPSO算法和PSO算法中粒子运动过程如图1所示.

从图1可看出,MeanPSO算法中粒子搜索区间更广,使得算法在进化前期有更大可能搜索到全局最优解[14].

1.3 粒子位置更新公式的改进

文献[13]提出一种带有平均维度信息的分层简化粒子群优化(PHSPSO)算法,PHSPSO算法舍弃PSO算法中粒子速度更新项,并引入平均维度信息概念,即每个粒子所有维信息的平均值,计算公式为式(4). 同时PHSPSO算法将粒子位置更新公式分解为3种模式,分别为式(5)、(6)、(7).

(4)

xid(t+1)=wxid(t)+c1r1(pbestid-xid(t)),

(5)

xid(t+1)=wxid(t)+c2r2(gbestd-xid(t)),

(6)

xid(t+1)=wxid(t)+c3r3(pad-xid(t)),

(7)

其中,式(5)有助于算法的全局开发能力;式(6)有助于算法的局部勘探能力,帮助算法跳出局部最优;式(7)有助于提升算法的收敛速度.在迭代过程中,算法基于概率选择不同的模式来更新粒子位置.

文献[8]指出采用“X=X+V”来更新粒子位置有助于提高算法的局部勘探能力,而“X=wX+(1-w)V”有助于提高算法的全局开发能力,基于此本文提出一种自适应粒子位置更新机制,如式(8)、(9)所示.

(8)

(9)

式中,fit(·)为粒子的适应度值,N为种群中粒子个数.式(8)中pi表示当前粒子适应度值与种群中所有粒子平均适应度值的比值,当pi较大时,当前粒子的适应度值远大于种群中所有粒子平均适应度值,此时应采用“X=wX+(1-w)V”更新粒子位置以增强算法的全局开发能力,否则采用“X=X+V”来更新粒子位置,来保证算法的局部勘探能力.

2 改进算法

2.1 粒子速度和位置自适应更新策略

本文结合以上分析提出一种新的自适应粒子速度和位置更新策略,如式(10)、(11)所示.

(10)

(11)

上述自适应策略借鉴文献[8]中pi作为自适应判定条件.当pi>δ时,当前粒子的适应度值远大于种群中所有粒子平均适应度值,表明算法处于搜索初期或者当前粒子分布较为分散,此时应采用式(10)更新粒子速度和位置.式(10)在速度更新项中引入个体最优和群体最优的线性组合,能够使粒子的搜索空间更广,从而提高算法搜索到全局最优解的可能性,而位置更新则采用“X=wX+(1-w)V”来提高算法的全局搜索能力;当pi<δ时,当前粒子的适应度值与种群中所有粒子平均适应度值相差不大,表明算法处于搜索中后期或者当前粒子分布较为集中,此时应采用式(11)更新粒子速度和位置.在式(11)中,位置更新采用“X=X+V”来保证算法局部勘探能力,防止算法在求解复杂多峰函数时陷入局部最优,而将粒子平均维度信息pad引入到粒子速度更新公式中,提高算法的收敛速度[13].

图2 惯性权重随迭代次数变化图Fig.2 The variation of inertia weight with iteration times

2.2 惯性权重的选取

惯性权重w是PSO算法的重要参数之一,它可以平衡算法全局开发能力和局部勘探能力,标准PSO算法采用线性递减w,这种线性调整的方式可以在一定程度上平衡算法开发能力与勘探能力,而在面对复杂非线性多维函数优化问题时,算法容易陷入局部最优解. 因此,为更好改善算法性能,一些学者提出惯性权重非线性调整策略. 本文采用文献[8]提出的基于Logistic混沌映射非线性变化惯性权重w.

混沌映射作为一种非线性映射,因其所产生的混沌序列具有良好随机性和空间遍历性,在进化计算中得到广泛应用,其中Logistic映射应用较为广泛,它可以产生[0,1]之间的随机数. 式(12)给出了Logistic映射的定义,w的定义如式(13).

r(t+1)=4r(t)(1-r(t)),r(0)=rand, 其中,r0≠{0,0.25,0.75,1},

(12)

(13)

式中,wmax=0.9,wmin=0.4;r(t)是由式(12)迭代产生的随机数.惯性权重随迭代次数的变化如图2所示.

2.3 算法实现

算法实现步骤如下:

步骤1 参数初始化,包括种群规模N,最大迭代次数Tmax=1 000,学习因子c1和c2,惯性权重w;并在搜索空间内随机初始化粒子位置、速度;

步骤2 根据给定目标函数计算所有粒子适应度值;

步骤3 比较种群中所有粒子的适应度值与其经历过的最优位置适应度值的优劣,若前者更优,则用粒子的当前位置替代粒子的个体历史最优位置;

步骤4 比较种群中所有个体最优位置的适应度值与整个群体经历过的最优位置的适应度值的优劣,若前者更优,则更新全局最优位置;

步骤5 根据式(8)计算pi,若pi>δ,则利用式(10)更新粒子的速度和位置;否则,利用式(11)更新粒子的速度和位置;

步骤6 判断是否满足终止条件,若满足,则算法终止并输出最优值;否则,转至步骤2.

3 仿真实验及结果分析

3.1 基本测试函数

为验证所提算法有效性,本文选取12个具有不同特性的测试函数[13,15],将本文算法与线性递减惯性权重粒子群优化(LDWPSO)算法[7]、均值粒子群优化(MeanPSO)算法[11]、社会学习粒子群优化(SL-PSO)算法[16]、基于概率分层的简化粒子群优化(PHSPSO)算法[13]、基于终端交叉和转向扰动的粒子群优化(TCSPSO)算法[15]、一种基于自适应策略的改进粒子群优化(MPSO)算法[8]进行对比测试. 12个测试函数的相关描述如表1所示. 其中函数f1、f2、f3、f4、f5是单峰函数,主要用于测试算法的收敛速度和寻优精度;函数f6、f7、f8、f9、f10、f11、f12是多峰函数,主要用于测试算法跳出局部最优避免“早熟”收敛的能力.

表1 12个基本测试函数Table 1 12 basic test functions

续表1 Table 1 continued

3.2 阈值参数δ取值对算法性能的影响

文献[8]中阈值δ取值为[0,1]之间的随机数,本文认为阈值δ随机变化不利于对当前粒子状态准确判断,从而影响算法性能.本文将进行一组实验来验证此观点,进而确定阈值δ最佳取值.实验选取表1中4个测试函数(D=100),算法独立运行50次,取最优结果的平均值作为比较,具体结果见表2.由表2知,δ取0.8时,对于单峰函数f4,算法收敛精度最高;而对于多峰函数f10、f12,算法收敛速度最快;对于函数f11,算法的收敛精度要远优于δ取1和rand时的结果.故本文δ取0.8. 表2中括号内数字代表算法求得最优解时的平均迭代次数(取整).

3.3 与其他改进PSO算法对比

本文使用Matlab软件进行仿真,不同PSO算法设置相同种群规模N=100、最大迭代次数Tmax=1 000和变量维数D=30,其他参数设置与原文保持一致,具体见表3. 每个算法独立运行50次,记录50次运行结果的平均值(Mean value)和标准差(Standard deviation)来评价算法性能,结果见表4. 为更直观对比各算法求解精度和收敛速度,图3给出各算法求解12个测试函数时适应度值变化曲线.

表3 各PSO算法的参数设置Table 3 Parameter setting of each PSO algorithm

表2 参数δ不同取值的优化结果比较Table 2 Comparison of optimization results with different values of parameter δ

表4 7种算法求解12个测试函数的结果对比(D=30)Table 4 Results comparison of 7 algorithms for 12 test functions(D=30)

续表4 Table 4 continued

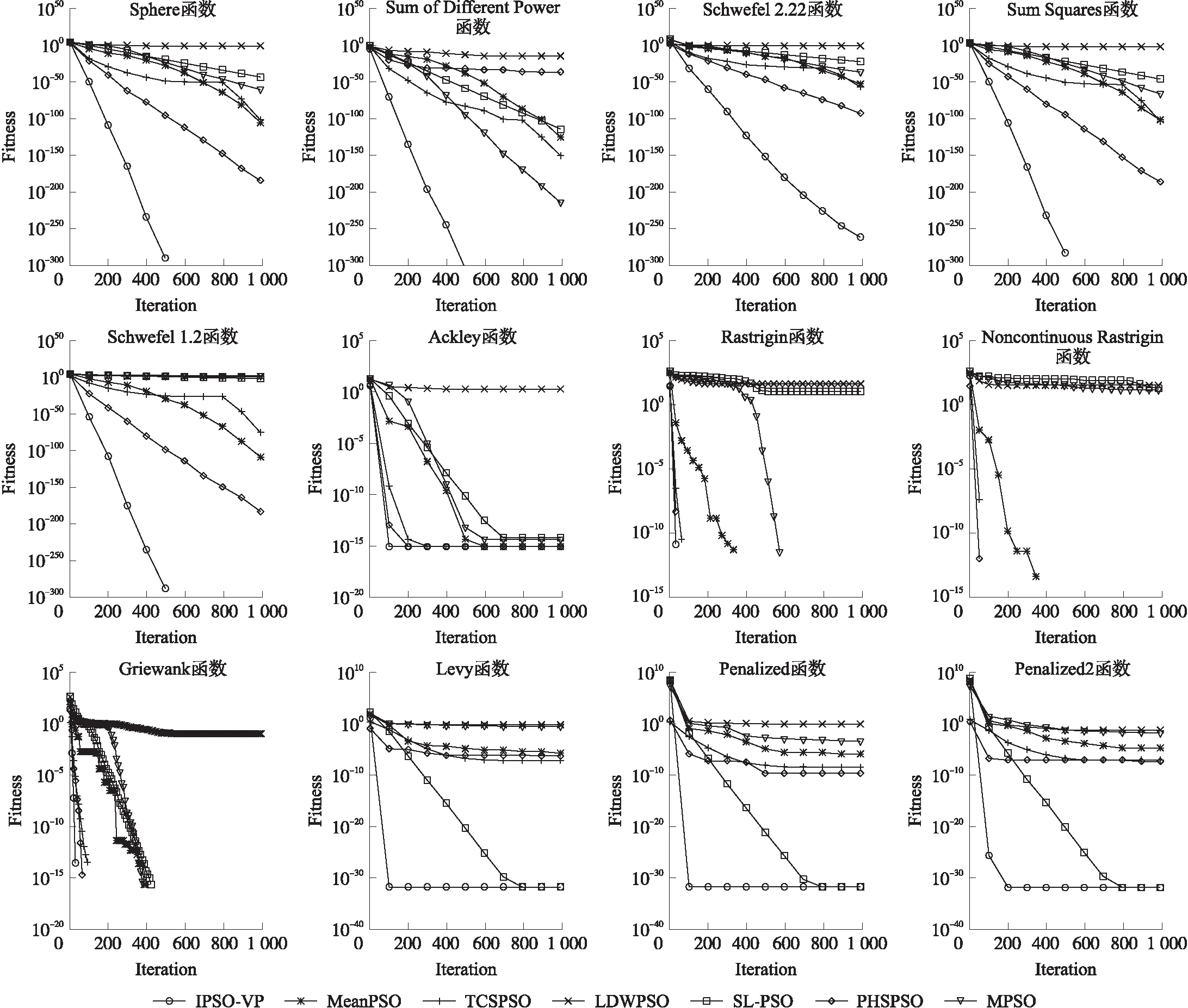
图3 12个测试函数的收敛曲线(30维)Fig.3 Convergence curves of 12 test functions(30 dimensions)

分析表4和图3可知改进算法(IPSO-VP)在30维f1、f2、f3、f4、f55个单峰函数上,无论是求解精度、收敛速度还是稳定性均优于6个对比算法,且在函数f1、f2、f3、f5上IPSO-VP算法均能求得最优值. 对于多峰函数f6、f7、f8、f9,虽然IPSO-VP与MeanPSO、PHSPSO、TCSPSO 算法均能求得函数最优值且求解性能稳定,但从图3可看出IPSO-VP算法收敛速度更快. 对于多峰函数f10、f11、f12,IPSO-VP算法求解性能明显优于除SL-PSO算法外的5个算法,虽然SL-PSO算法的求解精度与IPSO-VP算法相同,但从图3收敛曲线可看出IPSO-VP算法收敛更快,约迭代100～200次之后就完成收敛.

为进一步验证IPSO-VP算法优越性,将7种算法分别在60维和100维的12个测试函数上进行寻优测试,表5、表6分别记录了各算法在60维、100维的12个测试函数上独立运行50次所得结果的平均值和标准差.

表5 7种算法求解12个测试函数结果的平均值和标准差(D=60)Table 5 Mean value and standard deviation of 7 algorithms for 12 test functions(D=60)

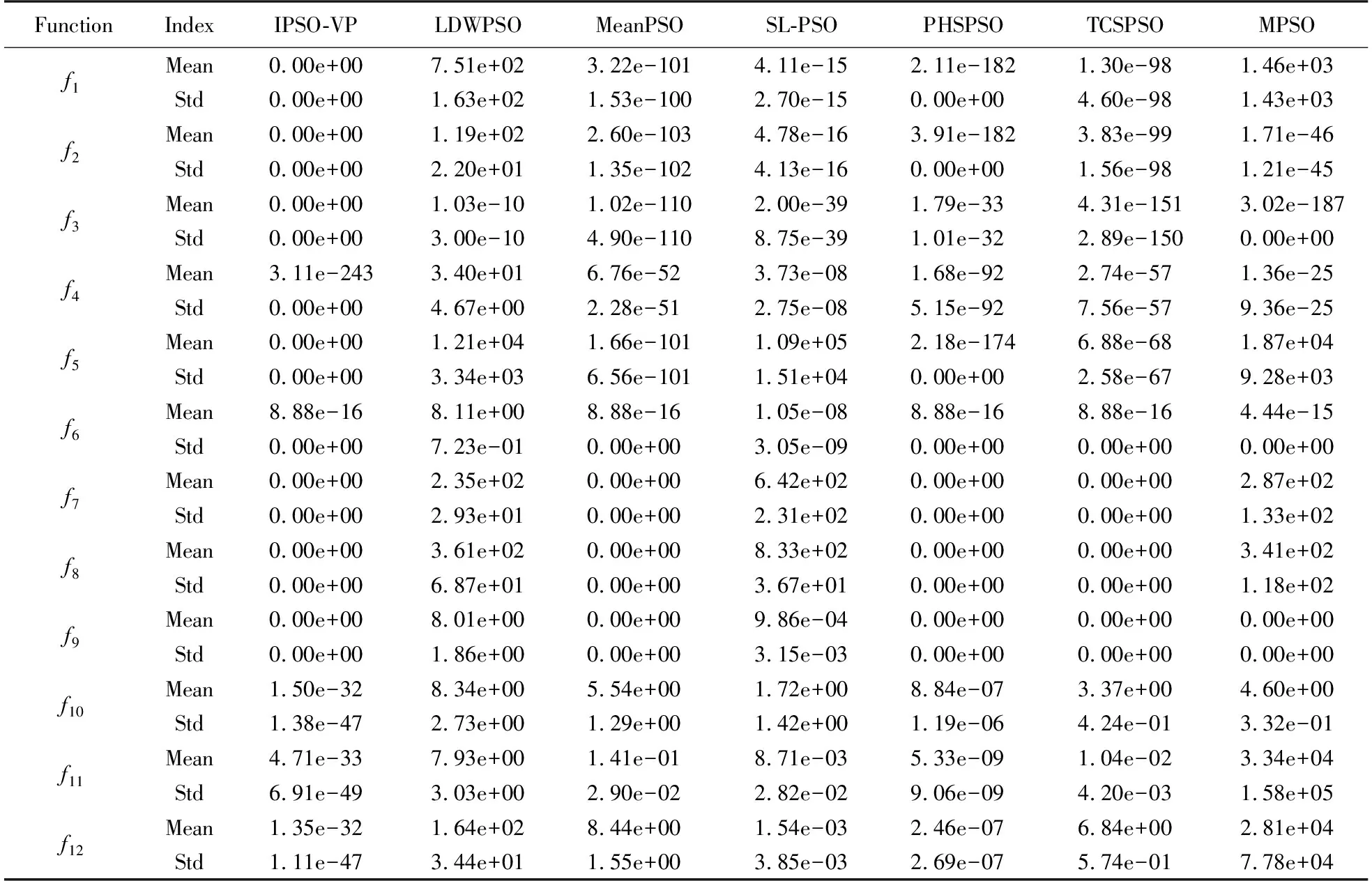
表6 7种算法求解12个测试函数结果的平均值和标准差(D=100)Table 6 Mean value and standard deviation of 7 algorithms for 12 test functions(D=100)

从表5和表6可看出,对于函数f1、f2、f3、f5、f7、f8、f9,无论是60维还是100维,IPSO-VP算法均能求得函数最优解;f10、f11、f123个多峰函数的局部极小值个数会随着变量维数的增加呈指数级增长[17],求解难度增大,但IPSO-VP算法对这3个函数的求解结果依然有很高的精度,且明显优于其他6个算法. IPSO-VP、MeanPSO、PHSPSO、TCSPSO算法在函数f6、f7、f8、f9上的求解结果相同,为进一步比较这4种算法优劣,图4给出了4种算法求解100维的4个多峰函数的适应度值变化曲线,可以看出IPSO-VP算法收敛速度更快.

图4 4个测试函数的收敛曲线(100维)Fig.4 Convergence curves of four test functions(100 dimensions)

3.4 算法时间复杂度分析

标准PSO算法时间复杂度为O(nmD)[18],其中n为粒子数,m为算法迭代次数,D为问题维数,本文IPSO-VP算法利用式(10)、(11)来更新粒子速度和位置,与标准PSO算法相比仅多一项自适应判定,因此,改进策略并未增加算法时间复杂度,本文算法时间复杂度仍为O(nmD).并且,由图3收敛曲线可看出,在求解精度相同情况下,本文算法所需迭代次数更少. 综上分析,当种群规模、问题维数和迭代次数相同时,本文算法的时间复杂度并未增加.

4 结论

本文提出一种改进粒子速度和位置更新公式的粒子群算法,算法中引入一种自适应粒子速度和位置更新策略,同时采用基于Logistic混沌的非线性惯性权重,实验结果表明,改进算法具有较快的收敛速度和较高的寻优精度,同时改进算法解决维数较高的多峰函数问题具有良好性能和潜在应用价值. 未来工作中,应用改进算法求解实际优化问题是值得研究的内容.