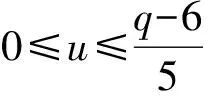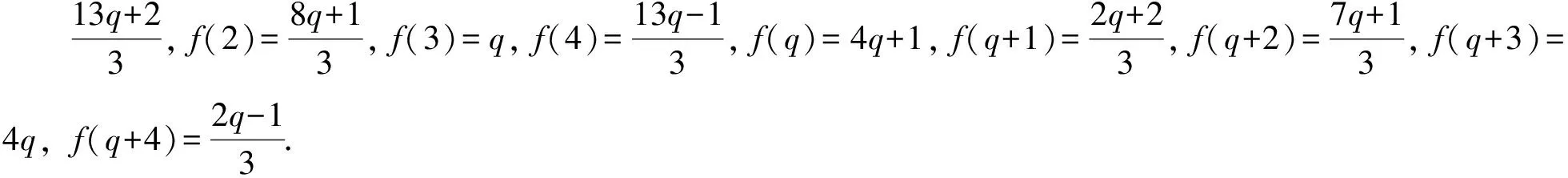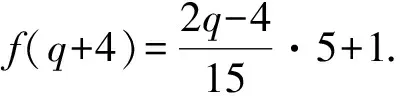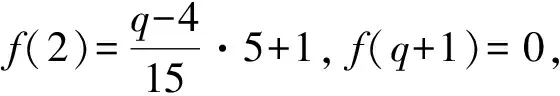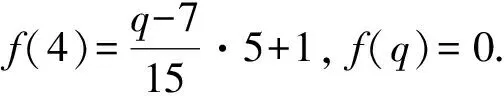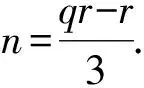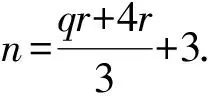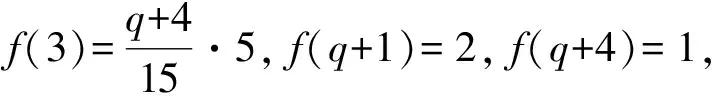一类三阶分圆多项式的高度
张 彬,孙雯宇,杜金征南,毕昕宇
(1.曲阜师范大学数学科学学院,山东 曲阜 273165) (2.山东财经大学数学与数量经济学院,山东 济南 250014)
n次分圆多项式Φn(x)是以所有的n次本原单位根为单零点的首一整系数多项式,令符号a(n,j)表示Φn(x)中xj的系数,即
其中φ为欧拉函数.利用数学归纳法可证Φn(x)为有理数域上的不可约多项式.由于n是满足Φn(x)|xn-1的最小正整数,我们称Φn(x)为n次分圆多项式.
令A(n)表示分圆多项式Φn(x)所有系数绝对值的最大值,并称A(n)为Φn(x)的高度.如果A(n)=1,那么我们称分圆多项式Φn(x)为平坦的.为了研究A(n),根据分圆多项式的性质,我们只需考虑n为无平方因子的奇素数的情形.对于无平方因子的奇素数n,我们称n的互异素因子个数为分圆多项式Φn(x)的阶.事实上,一阶和二阶分圆多项式都是平坦的.很久之前,人们就已经发现并不是所有的分圆多项式都是平坦的,比如a(105,7)=-2,因而三阶分圆多项式Φ105(x)就是非平坦分圆多项式.
三阶分圆多项式中既有平坦的也有非平坦的,其系数性质相比一阶和二阶分圆多项式变得相对复杂起来,关于它的高度问题的研究是一项非常有意义的课题,但是完全决定三阶分圆多项式的高度具有很大的困难.因此目前大多数相关方面的研究都是在某些特定条件之下进行的.接下来我们考虑关于Φpqr(x)在如下情形方面的研究:设p 2007年,Kaplan[1]在条件r≡±1(modpq)之下证明了如下结果: A(pqr)=1. 2012年,黄立君[2]和Elder[3]独立地在条件r≡±2(modpq)之下证明了如下结果: 结合Elder[3]中的结果,我们可得 命题1设p 2017年,作者在文[4]中研究了满足条件r≡±3(mod 5q)的三阶分圆多项式的性质,首次在不固定素数p的条件下,给出了一类无穷多的高度为3的三阶分圆多项式Φpqr(x).本文中,在p=5且r≡±3(mod 5q)的条件下进一步讨论三阶分圆多项式的系数问题并证明如下结果: 定理1设5 在本部分,我们给出证明定理1过程中需要的几个引理. 引理1[1]设p 引理2[3,5]设p 引理3[1]设p rf(i)+i≡n(modpq), 的唯一整数.我们有 引理3是一个十分重要的结果.它把三阶分圆多项式的系数的计算问题转化为二阶分圆多项式的系数计算问题.目前二阶分圆多项式已经被国内外学者广泛研究,给出了相关的比较完整的结果.特别地,关于其系数的取值问题,我们有如下的结果: 引理4[6]设p pq+1=ps+qt. 利用引理1可知,为了证明在 r≡±3(mod 5q) 条件下有2≤A(5qr)≤3,我们只需要考虑情形: r≡3(mod 5q). 一方面,在引理2中取ω=3,可得A(5qr)≤3. 另一方面,为了证明A(5qr)≥2,根据函数A(n)的定义,我们只需要在分圆多项式Φ5qr(x)中找到一个大于1或者小于-1的系数.为实现这个目的,我们将利用引理3来证明如下命题: 命题2设5 (2)若q≡2(mod 15),则a(5qr,qr+3)=2; 因此当k∈{0,1,3,4,q+1,q+2,q+4}时,有rf(k)>n;当k∈{2,q,q+3}时,有rf(k)≤n.故 那么借助引理3得 a(5qr)=a(5q,f(2))-a(5q,f(q))-a(5q,f(q+3)). a(5qr)=2-a(5q,f(q+3)). f(q+3)=5u, 若a(5q,f(q+3))=-1,则必有 f(q+3)=5u+vq+1, 那么借助引理3得 a(5qr)=a(5q,f(3))-a(5q,f(q+1))-a(5q,f(q+4)). a(5qr)=2-a(5q,f(q+1)). 若a(5q,f(q+3))=1,则必有 f(q+1)=5u+vq. 由0 故当k∈{0,1,3,4,q,q+2,q+3,q+4}时,有rf(k)>n;当k∈{2,q+1}时,有rf(k)≤n. 借助引理3得 a(5qr)=a(5q,f(2))-a(5q,f(q+1)). 那么借助引理3得 a(5qr)=a(5q,f(1))+a(5q,f(4))-a(5q,f(q)). a(5qr)=-2+a(5q,f(1)). 借助引理3得 a(5qr)=a(5q,f(0))+a(5q,f(3))-a(5q,f(q+1))-a(5q,f(q+4)). a(5qr)=2+a(5q,f(3))-a(5q,f(q+1)). 借助引理3得 a(5qr)=a(5q,f(3))-a(5q,f(q+1))-a(5q,f(q+4)). 借助引理3得 a(5qr)=a(5q,f(3))-a(5q,f(q+2)). 借助引理3得 a(5qr)=a(5q,f(4))-a(5q,f(q+2)). 这样便完成了命题2的证明,从而定理1成立. 致谢:本文作者诚挚地感谢纪春岗教授的指导!并对审稿专家的建议致以衷心的谢意!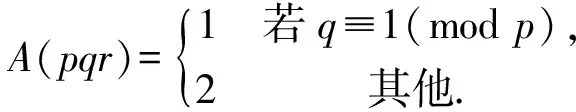
1 引理
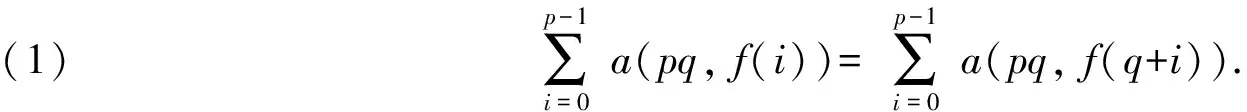
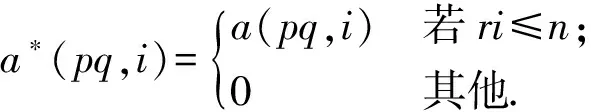


2 定理1的证明