含不可微非线性项的四阶边值问题单侧全局区间分歧

沈文国,包理群,纳仁花

(1.兰州工业学院基础学科部,甘肃 兰州 730050) (2.兰州工业学院电子信息工程系,甘肃 兰州 730050)

其中,非线性项 F=f+g, f,g∈C(R),|f(s)/s|≤M1,0<|s|≤1,M1是一个正的常数;|f(s)/s|≤M2,C<|s|,C是充分大的正常数,M2是一个正的常数;对于 s≠0,成立sg(s)>0;存在g0,g∞∈(0,∞)使得g0=lim|s|→0g(s)/s,g∞=lim|s|→∞g(s)/s. 应用上述结果,研究一类非线性四阶边值问题结点解的存在性.

下列四阶边值问题表示两端简单支撑梁的方程

(1)

2012年,代国伟[1]建立了与问题(1)对应的下列线性特征值问题的谱理论

(2)

随后,代国伟等[2]建立了问题(1)的单侧全局分歧结果. 然而,上述问题都是非线性项在零处和无穷远处满足渐进线性增长条件.

Berestycki[3]研究了一类非线性项在零处和无穷远处满足非渐进线性增长条件的二阶问题的区间分歧问题. Schmitt 和 Smith[4]部分地提升了[3]的研究结果. 最近,马如云等[5]研究了一类非线性项在零处和无穷远处满足非渐进线性增长条件的二阶问题的区间分歧问题,提升了[3]的研究结果. 随后,代国伟等[6-7]研究了与[3]和[5]相似的问题.

文献[8]研究了下列问题

(3)

其中,非线性项F=f+g,f,g∈C([0,1]×R3)且满足下列条件:

(H1)a∈C([0,1],(0,∞))在[0,1]的任何子区间上都有a(t)≠0成立.

(H2) 对任何t∈[0,1],0<|x|≤1,|s|≤1以及λ∈R,都有|f(t,x,s,λ)/x|≤M1成立,其中M1是一个正常数.

(H3) 在(x,s)=(0,0)附近,对于t∈[0,1]和λ在有界集上取值时,g(t,x,s,λ)=o(|x|+|s|)一致成立.

当满足条件(H1)-(H3)时,作者[8]获得了问题(3)从零点发出的单侧全局分歧定理如下:

1 预备知识

定义线性算子L:D(L)⊂E→Y

Lx=x(4),x∈D(L),

其中D(L)={x∈C4[0,1]|x(0)=x(1)=x″(0)=x″(1)=0}.则L是闭算子且L-1:Y→E是全连续算子.令I=(0,1).

接下来,从文献[1,2]中引述下列预备知识.

定义1[2]令u∈E和t*∈I使得u(t*)=u″(t*)=0成立.若u′(t*)≠0 或u‴(t*)≠0,则称t*是一个推广的简单零点.否则,称t*是一个推广的加倍零点.假如u不存在一个推广的加倍零点,则称u是一个结点解.

当a满足(H1),下列引理成立:

引理1[1-2]令(H1)成立.则

(1)问题(2)存在一个无穷正特征值序列

0<λ1<λ2<…<λk→+∞,k→+∞.

(2)每个特征值是简单的.每个特征值λk(a) 对应着唯一一个特征函数ψk,并且其在(0,1)中有k-1个推广的简单零点且在0附近是正的.

引理2[2]若 (λ,x) 是(3)在满足假设(H2)和(H3)的非平凡解且x存在一个推广的加倍零点,则x≡0.

2 无穷远处单侧全局区间分歧

在空间R×E中增加无穷远点{(λ,∞)|λ∈R}.假设问题(3)的非线性项F满足F=f+g,其中f,g∈C([0,1]×R3),且满足下列条件:

(H4) 对任何t∈[0,1],C<|x|,C<|s|以及任意λ∈R,都有|f(t,x,s,λ)/x|≤M2成立,其中M2是一个正常数.

(H5) 在(x,s)=(∞,∞)附近,对于t∈[0,1]和λ在有界集上取值时,g(t,x,s,λ)=o(|x|+|s|)一致成立.

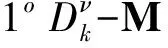
要么成立

证明相似于[9,定理1.6]的证明,但是为了方便,给出一个大概的框架.

假设 (λ,x)∈J且 ‖x‖≠0,用 ‖x‖2除以(3)两边且令y=x/‖x‖2,则

(4)

定义

和

显然,(4)等价于

(5)

显然,(λ,0) 是(5)的一个解.通过简单计算,由(H4),(H5)可得

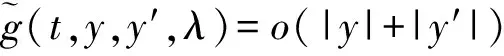
3 应用

在这部分,通过定理1,定理2,可得下列问题结点解的存在性

(6)

其中a满足(H1).假设非线性项F满足F=f+g,其中f,g∈C(R)且满足:

(A1)|f(s)/s|≤M1,0<|s|≤1,其中M1是一个正常数.

(A2)对一些充分大的正常数C,成立|f(s)/s|≤M2,C<|s|,其中M2是一个正常数.

(A3)对于s≠0,成立sg(s)>0.

(A4)存在g0,g∞∈(0,∞) 使得

以下是本文主要结果:

定理3令a0=mint∈[0,1]a(t),a0=maxt∈[0,1]a(t).假设(H1),(A1),(A2),(A3),和(A4)成立.对一些k∈N,假设g0a0>M1a0和g∞a0>M1a0成立,要么成立

(7)

要么成立

(8)

定理4假设(H1),(A1),(A2),(A3),和(A4)成立.对一些k∈N,假设g0a0>M1a0并且g∞a0≤M2a0成立,对于

定理3的结论是有效的.

定理5假设(H1),(A1),(A2),(A3),和(A4)成立.对一些k∈N,假设g0a0≤M1a0并且g∞a0>M2a0成立,对于

定理3的结论是有效的.

注2由(A4),可得存在一个正常数M3,对所有s≠0,使得g(s)/s≥M3成立.

注3假如Mi≡0(i=1,2),则定理4 和5 的情况不会发生,并且定理3 等价于[2,定理4.1](当权函数为g(t)>0).

为了证明定理3,需要下列结果.

引理3假设(H1),(A1),(A2),(A3),和(A4)成立.对一些k∈N,假设g0a0>M1a0和g∞a0>M2a0成立,要么(7)成立,要么(8)成立,则

证明首先,研究下列问题的分歧现象

(9)

其中λ>0 是一个参数.

(1)显然,由条件(A1)可得

(10)

令ζ∈C(R,R) 使得

g(x)=g0x+ζ(x),

(11)

进而可得

(12)

因此,由(9),(10),(11)和(12)可知条件(H2)和(H3)成立.进而,令d1=M1a0/g0a0

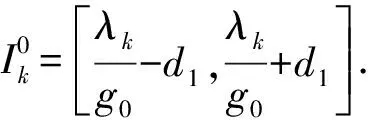
(2)显然,由条件(A2)可得

(13)

令ξ∈C(R,R) 使得

g(x)=g0x+ξ(x),

(14)

(15)

进而,由(15)可得

(16)

由定理2,可得下列结果.

(1)下列将证明定理2 中的 1O发生.

(2)下列证明定理2的2O不发生.

反设定理2的 2O发生,则可以推出矛盾.分如下两步来证明.

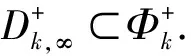
相反,假设

进而

y(4)n(t)=μna(t)g(yn)+a(t)f(yn).

令

0=τ(0,n)<τ(1,n)<τ(2,n)…<τ(k-1,n)<τ(k,n)=1,

记为yn在(0,1)中的推广的简单零点.则,若有必要,选择如下的一个子序列,

可以断言存在l0∈{0,1,…,k}.使得

τ(l0,∞)<τ(l0+1,∞).

否则,下式成立

产生矛盾.

定理3的证明:

显然,问题(8)形如 (1,x) 的解将产生问题(5)的一个解x.

此时,d1<1,d2<1.由(6),可得

(17)

由(7),可得

(18)

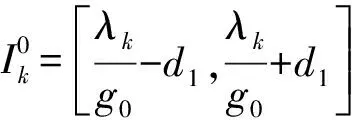
定理4的证明类似于定理3的证明.此时,由d1<1,d2≥1,可知(17)成立.由d2≥1,可知(18)不可能成立.

定理5的证明类似于定理3的证明.

此时,d1≥1,d2<1,进而(18)成立.由d1≥1,可知(17)不可能成立.

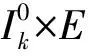
通过应用与定理3,4和5相似的方法,可以获得如下[11,定理3.1]的推广结果.

定理6假设(H1),(A1),(A2),(A3),和(A4)成立.对一些k∈N和j∈{0}∪N,假设g0a0>M1a0和g∞a0>M1a0成立,要么成立

(19)

要么成立

(20)

定理7假设(H1),(A1),(A2),(A3),和(A4)成立.对一些k∈N和j∈{0}∪N,假设g0a0>M1a0并且g∞a0≤M2a0成立,对于

则定理6的结论成立.

定理8假设(H1),(A1),(A2),(A3),和(A4)成立.对一些k∈N和j∈{0}∪N,假设g0a0≤M1a0并且g∞a0>M2a0成立,对于

则定理6的结论成立.